Data Fusion of MultiPle Curvature Mode ShaPes for Structural Damage Diagnosis

Cao Maosen（曹茂森），Zhang Zhui（张 锥），Sha Ganggang（沙刚刚）

Department of Engineering Mechanics，Hohai University，Nanjing 210098，P.R.China

Data Fusion of MultiPle Curvature Mode ShaPes for Structural Damage Diagnosis

Cao Maosen（曹茂森）*，Zhang Zhui（张 锥），Sha Ganggang（沙刚刚）

Department of Engineering Mechanics，Hohai University，Nanjing 210098，P.R.China

This study aims to develop a reliable method for locating multiple cracks in a beam using data fusion of multiple curvature mode shapes.The identification of multiple damage in beams based on curvature mode shape has become a research focus in recent decades.However，the curvature mode shape method using a single mode carries limited damage information，and fails to reveal all cracks when multiple damage detection is required.To address this limitation，the curvature mode shape method is further enhanced by a data fusion algorithm to fuse damage information in multiple modes.The effectiveness of the method is proved through a numerical case of a beam with multiple cracks.The applicability of the method is experimentally validated by detecting multiple cracks in a composite laminated beam with mode shapes acquired by a scanning laser vibrometer.The results show that the method of fusing multiple curvature mode shapes carries more complete damage information than the traditional one using a single mode，and can successfully locate all cracks in a damaged beam.

structural damage diagnosis；multiple cracks；curvature mode shape；data fusion；scanning laser vibrometer

0 Introduction

Structural damage detection has been a research focus in fields including civil aviation，mechanics，aerospace，and military fields during the last few decades［1-5］.Damage detection based on curvature mode shapes has been widely discussed in literature［6-9］.The curvature mode shape is the curvature of a displacement mode shape for a structure.In the case of a beam，its curvature mode shape can be denoted as［6］

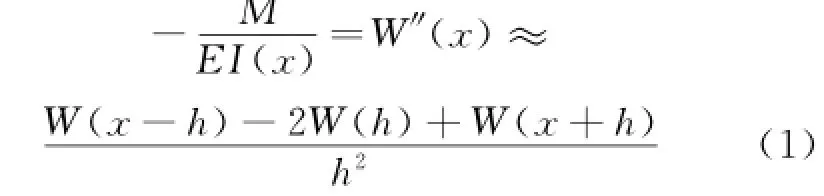
where M is the bending moment；EI（x）the bending stiffness；W（x）the displacement mode shape for the beam，and W″（x）the curvature mode shape.W"（x）can be approximately obtained by the second-order central difference of W（x）with sampling interval h.Damage，commonly represented by an alteration in EI（x），can cause a change in W″（x），which in turn manifests the status of the damage.Thus the use of curvature mode shapes is theoretically feasible for characterizing damage in beams［10］.

Despite the proven ability of the curvature mode shape to locate damage，its effectiveness is affected by the selected mode shape［11］.In essence，a mode shape has positional sensitivity to damage which is determined by the magnitude of the curvature mode shape at the damage location［12］.If damage occurs at the node of a particular mode shape，it is difficult to detect any change in its curvature mode shape.This is a phenomenon referred as the node effect of a curvature mode shape-based method［13］.In multiple damage detection using curvature mode shapes，damage is more likely to be located at mode nodes，and thus the difficulty of multiple damage detection increases.In structural damage diagnosis applications，the location of damage is commonly unknown in advance，due to the inverse problem of damage detection，and therefore it is difficult to choose an appropriate mode shape with a high magnitude of curvature mode shape at the damage location. That means locating damage relying on a single curvature mode shape is unreliable in practical damage diagnosis.

To deal with this problem，this study introduces the concept of data fusion to curvature mode shape-based multiple damage detection to improve the reliability of damage localization for beam-type structures［14-16］.

1 MultiPle Mode Fusion for Curvature Mode ShaPe

1.1 Curvature mode shaPe change

The discrete expression of curvature mode shape can usually be written as

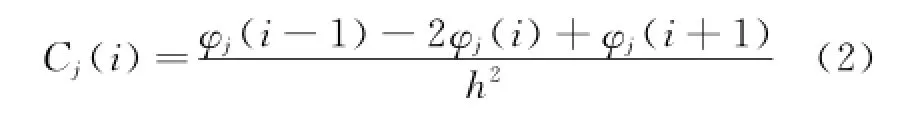
where Cj（i）denotes the curvature in the i th point of the j th mode shapeφj；and Cjis termed as the curvature mode shape ofφj.

Curvature mode shape change（CMSC）can be regarded as an index of structural damage. The curvature mode shape change of the i th point with the j th mode CMSCj（i）is defined as

1.2 DemPster-Shafer evidence theory

Dempster and Shafer proposed evidence theory in the 1970s as an extensional development of probability theory［16-17］.Suppose A1，A2，…，Anto be n events，S1，S2，…，Smto be m sensors and Mj（Ai）to be the probability of the i th event occurring from the j th sensor.Then，the probability of the event P occurring is

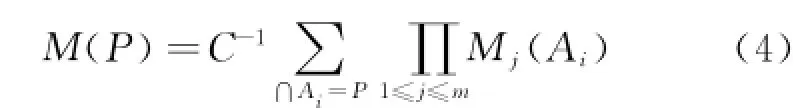
where

1.3 Multi-mode information fusion based on DemPster-Shafer evidence theory

Dempster-Shafer evidence theory is further applied to the obtained CMSCs as follows：

Consider that there are m modes C1，C2，…，Cmcontaining n points.The n points can be denoted as A1，A2，…，An.Damage occurring at point Aican be denoted as event Ai.The damage probability of every point is regarded as the probability of the Aievent occurring from the j th mode Cj.

Mj（Ai）is already known as

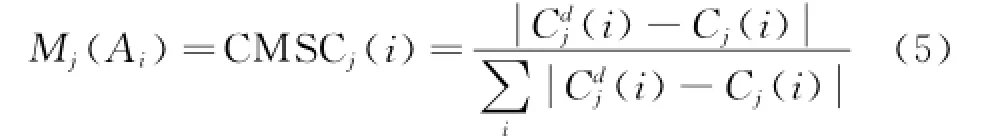
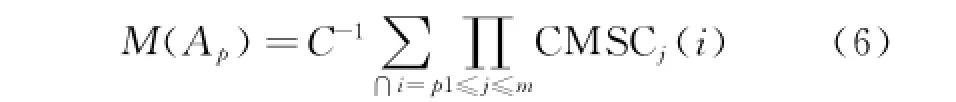
where

Therefore，the damage probability of any point M（Ap）can be calculated by Eq.（4）as

We term the result of the data fusion on CMSCj（i）（j=1，2，…，m；i=1，2，…，n）as CMSC*（i）（i=1，2，…，n）.

2 Numerical Verification

An analytical cantilever beam model bearing three cracks is employed for method verification by numerical simulation，where cracks are treated as rotary springs［17］（Eig.1）.The beam dimensions are：Length L=500 mm，width B= 50 mm，height H=10 mm.Elastic modulus，Poisson′s ratio，and material density are taken as 200 GPa，0.37，and 800 kg/m3，respectively.In Eig.1，W is the displacement mode shape；K thebending constant of the spring；x the horizontal axis；ξthe dimensionless coordinate，andζ=a/ H the crack depth ratio with the crack depth a. Three cracks are located at Lc1=125 mm（ξ1= 0.25），Lc2=225 mm（ξ2=0.45），and Lc3= 300 mm（ξ3=0.6），with depths 2 mm（ζ1= 0.2），2.5 mm（ζ2=0.25），and 3 mm（ζ3= 0.3），respectively.

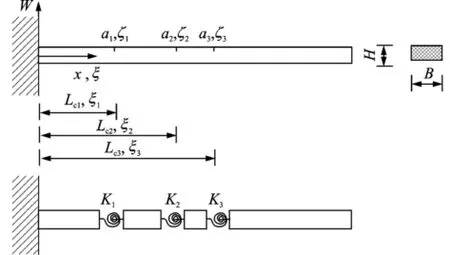
Eig.1 Cracked cantilever beam sample

Eig.2 Mode shapes and curvature mode shapes of damaged structure and CMSCs

The first ten mode shapes are obtained by analytical solutions［17］（Eig.2（a）），and CMSCs areobtained by Eq.（3）and shown in Eig.2（c）.Erom Eig.2（c），it can be clearly seen that not all the cracks can be obviously detected in each mode，and the cracks can scarcely be detected by the 9th and the 10th mode.In practical damage diagnosis，without prior knowledge of the existence of the cracks，it is less possible to identify the cracks relying on a single mode shape.

Subsequently，CMSCs of the 1st，the 6th，the 9th，and the 10th modes（Eig.3（a））are processed by the Dempster-Shafer evidence theory（Eq.（6））to obtain CMSC*.Eused damage identification results are shown in Eig.3（b），where the three peaks rising at the locations of the cracks clearly pinpoint all three cracks atξ= 0.25，0.45，and 0.6，respectively，in good agreement with their actual locations.

3 ExPerimental Validation

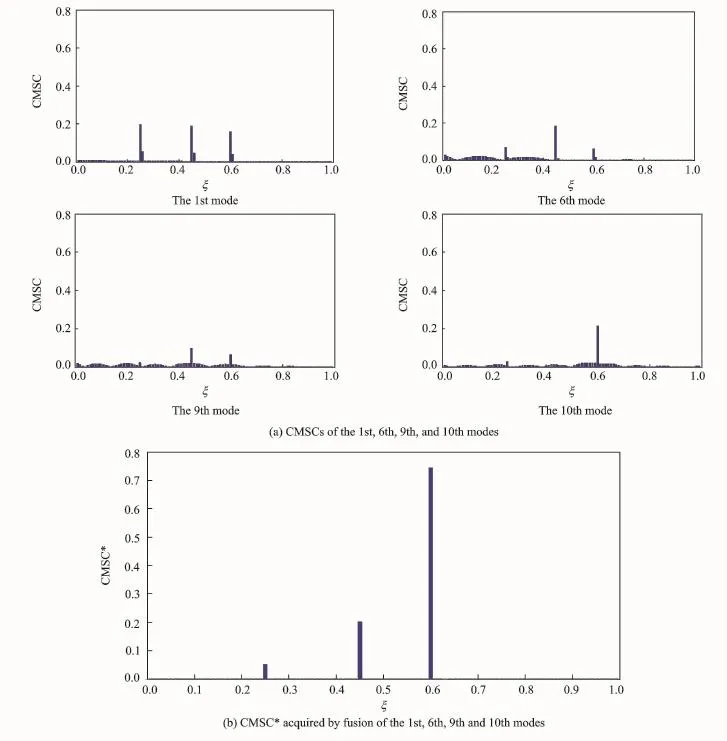
Eig.3 CMSCs of the 1st，6th，9th，and 10th modes，and their fused result CMSC*

3.1 Testing descriPtion

An experiment is conducted to identify and localize multiple cracks in a composite laminated beam to validate the applicability of the proposed multiple mode fusion curvature mode shape method.The beam specimen consists of 5 layers，each of which is 0.3 mm thick.The geometrical di-mensions of the beam are 500 mm long，10 mm wide，and 1.5 mm thick.Eor the particular cantilevered condition，the effective length of the beam is 490 mm.The beam used in the experiment is shown in Eig.4.Three cracks are created by cutting with a very sharp knife.

An electromechanical shaker is used to harmonically and perpendicularly excite the beam near its fixed end.When the beam vibrates，velocities are registered by a scanning laser vibrometer（SLV）at 499 measurement points evenly distributed along the midline of the beam.

3.2 Results

Eirst，the dynamic characteristics of the specimen are analyzed and 8 mode shapes are acquired by SLV.On the basis of these，damage diagnosis index CMSCs are obtained as shown in Eig.5.Erom Eig.5 it is clear that the traditional curvature mode shape method based on a single mode almost completely fails to identify the locations of the three cracks.The damage traits of the cracked cantilever beam cannot be detected at all，due to the overshadowing by the intense oscillations of curvature mode shapes.Hence，without prior information of the locations of the cracks，it is ineffective to try to identify the three cracks relying on a single mode shape.

Eig.4 Cracked laminated beam specimen

Eig.5 CMSCs of the 8th and the 10—16th modes

In contrast to any single CMSC curve，the overall CMSC*curve（Eig.6）arising from the data fusion of the CMSCs of the 8th，the 10th，the 11th，and the 14th modes is dominated by three prominent singular peaks.These peaks demonstrably locate the locations of the three cracks without ambiguity.

Eig.6 CMSC*acquired by fusion of the 8th，10th，11th and 14th modes

4 Conclusions

The traditional curvature mode shape method using a single mode carries limited damage information，which likely fails to reveal all the instances of damages as required for multiple damage detection.Arising from this concern，a multiple mode fusion curvature mode shape method is proposed to reveal all instances of damage.Eirst，an index CMSC is proposed to measure the difference of curvatures for beams of intact and damaged status.Then，CMSC is further enhanced by using the Dempster-Shafer evidence theory to fuse damage information contained in different modes，with the aim of detecting all damage locations. The effectiveness of the method is proved in a numerical case of a beam with multiple cracks.The applicability of the method is experimentally validated by detecting multiple cracks in a composite laminated beam using mode shapes acquired by a SLV.The results show that the multiple mode fusion curvature mode shape method carries more complete damage information than the traditional curvature mode shape method based on a single mode，and can successfully locate all instances of damage in beams.

Acknowledgements

This work was supported by the Key Program of the National Natural Science Eoundation of China（No. 11132003），the Qing Lan Project，and the Eundamental Research Eunds for the Central Universities（Nos. 2012B05814，2014B03914）.

［1］ Kopsaftopoulos E P，Eassois S D.Vibration based health monitoring for a lightweight truss structure：Experimental assessment of several statistical time series methods［J］.Mechanical Systems and Signal Processing，2010，24（7）：1977-1997.

［2］ Worden K，Manson G，Denoeux T.An evidencebased approach to damage location on an aircraft structure［J］.Mechanical Systems and Signal Processing，2009，23（6）：1792-1804.

［3］ Eassois S D，Sakellariou J S.Time series methods for fault detection and identification in vibrating structures［J］.Philosophical Transactions of the Royal Society A：Mathematical，Physical and Engineering Sciences，2007，365（1851）：411-448.

［4］ Wang S S，Ren Q W，Qiao P Z.Structural damage detection using local damage factor［J］.Journal of Vibration and Control，2006，12（9）：955-973.

［5］ Lotfollahi-Yaghin M A，Koohdaragh M.Examining the function of wavelet packet transform（WPT）and continuous wavelet transform（CWT）in recognizing the crack specification［J］.KSCE Journal of Civil Engineering，2011，15（3）：497-506.

［6］ Pandey A K，Biswas M，Samman M M.Damage detection from changes in curvature mode shapes［J］. Journal of Sound and Vibration，1991，145（2）：321-332.

［7］ Whalen T M.The behavior of higher order mode shape derivatives in damaged，beam-like structures［J］.Journal of Sound and Vibration，2008，309（3/ 4/5）：426-464.

［8］ Cao M S，Qiao P Z.Novel Laplacian scheme and multiresolution modal curvatures for structural damage identification［J］.Mechanical Systems and Signal Processing，2009，23（4）：1223-1242.

［9］ Roy K，Ray-Chaudhuri S.Eundamental mode shape and its derivatives in structural damage localization［J］.Journal of Sound and Vibration，2013，332（21）：5584-5593.

［10］Cao M S，Xu W，Ostachowicz W，et al.Damage identification for beams in noisy conditions based on Teager energy operator-wavelet transform modal curvature［J］.Journal of Sound and Vibration，2014，333（6）：1543-1553.

［11］Salawu O S，Williams C.Damage location using vibration mode shapes［C］//Proceedings of the 12th IMAC.Honolulu，Hawaii：［s.n.］，1994：933-939.

［12］Cao M S，Ye L，Zhou L M，et al.Sensitivity of fundamental mode shape and static deflection for damage identification in cantilever beams［J］.Mechanical Systems and Signal Processing，2011，25（2）：630-643.

［13］Inman D J.Engineering vibration［M］.［S.l.］：Prentice Hall，Upper Saddle River，2000.

［14］Xu H，Su Z Q，Cheng L，et al.Reconstructing interfacial force distribution for identification of multidebonding in steel-reinforced concrete structures using noncontact laser vibrometry［J］.Structural Health Monitoring，2013，12（5/6）：507-521.

［15］Guo H Y.Structural damage detection using information fusion technique［J］.Mechanical Systems and Signal Processing，2006，20（5）：1173-1188.

［16］Liu T，Li A Q，Ding Y L，et al.Multi-source information fusion applied to structural damage diagnosis［J］.Structure and Infrastructure Engineering：Maintenance，Management，Life-Cycle Design and Performance，2011，7（5）：353-367.

［17］Cao M S，Radzieński M，Xu W，et al.Identification of multiple damage in beams based on robust curvature mode shapes［J］.Mechanical Systems and Signal Processing，2014，46（2）：468-480.

（Executive editor：Zhang Bei）

TU312 Document code：A Article ID：1005-1120（2015）03-0305-07

*CorresPonding author：Cao Maosen，Professor，E-mail：cmszhy@hhu.edu.cn.

How to cite this article：Cao Maosen，Zhang Zhui，Sha Ganggang.Data fusion of multiple curvature mode shapes for structural damage diagnosis［J］.Trans.Nanjing U.Aero.Astro.，2015，32（3）：305-311.

http：//dx.doi.org/10.16356/j.1005-1120.2015.03.305

（Received 18 March 2015；revised 25 April 2015；accepted 1 May 2015）