非参数回归N-W核估计法在财政系统中的应用

卢维学,杨世娟

（黄山学院 数学与统计学院，安徽 黄山245021）

1 引 言

财政收入表现为政府部门在一定时期内所取得的货币收入，是政府为履行其职能、实施公共政策和提供公共服务的需要而筹集的一切资金的总和。财政收入与经济增长之间的关系是宏观经济领域的重要问题之一。一般而言，经济增长会带动财政收入的增长。我国要想保持财政收入稳定增长，必须鼓励、支持和引导大中小企业的发展，增加税源。然而，财政收入并非越多越好，不协调的财政收入会抑制经济的增长，只有具备与经济协调发展的财力，政府才能更好的履行其职能，提供更多的公共服务，改善经济发展所需的硬件设施，从而促进经济又好又快地发展。毋庸置疑，分析财政收入与经济增长之间的定量关系对财政政策的制定具有较高的参考价值。

近年来，国内众多学者从理论和实证分析上对财政收入与经济增长之间的关系进行了研究和探索。研究思路主要有：

1.利用因素分析法[1]直接建立二者间的回归模型，如贾继花[2]综合利用因素分析法和回归分析法,对山东省财政收入与经济增长之间的关系作了详细分析；

2.利用协整理论[3]建立财政收入与经济增长的长期均衡模型来分析二者的长期变动关系，如吉亚辉、朱正取[4]通过分析甘肃省1978-2006年的财政收入和GDP的变动趋势，建立二者间的协整和误差修正模型。

以上两种思路主要都是事先设定模型形式，再对参数进行估计，从而建立二者间的关系。事实上这两种思路所建立的模型都是参数回归模型。但参数回归模型建立的前提是各项假设条件都要成立，随机误差为正态分布等，若模型及参数的假定条件与实际背离，那么推断与预测就会有较大的偏差，拟合效果会很差。而非参数回归所需的假定条件要弱得多，不需要事先设定函数形式，且模型约束较少，对解释变量和响应变量的分布形式没什么限制。因此，非参数回归具有更大的适应性，尤其在解释变量与响应变量的函数关系形式不确定时。本文将采用非参数回归建立我国财政收入与经济增长之间的关系。

2 非参数回归模型

2.1 模型介绍

这里主要考察d=1，X为非随机的情形。设从总体(X,Y)中随机抽取一组样本(X1,Y1)，(X2,Y2)，…(Xn,Yn)，记εi(i=1,2…n)为独立同分布的随机波动项，且满足E(εi)=0,Var(εi)=δ2＜+∞，此时的回归模型为：

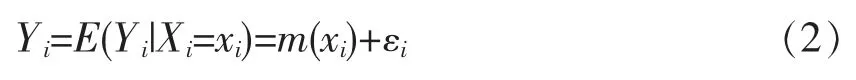
当m(x)的函数形式已知，仅需估计函数中未知参数时，此时为参数回归模型。不假设m(x)是某种函数形式，是对一般函数类型进行讨论，构造回归函数m(x)的估计量。

2.2 权函数估计

权函数在核估计[5]中起光滑的作用，即消除扰动的随机因素，使所得曲线反映变量之间的实际经济关系。对于给定的样本(X1,Y1)，(X2,Y2)，…(Xn,Yn)，权函数估计就是对回归函数m(x)进行估计，设Wni(x)=Wni(x;X1,X2,…Xn)是依赖于x和X1,X2,…Xn的函数，则m(x)的非参数回归估计量m＾n(x)可表示成下述形式：

其中Wni(x)称为权函数，满足=1。权数Wni(x)利用了解释变量的信息，且由解释变量的数值来确定每个Yi的权数的大小。

2.3 N-W核权函数回归估计

核估计是权函数估计的一种方法，在于找到核权函数作为(3)中的权函数。最常见的是Nadaraya和Watson在1964年提出的一类核权函数回归估计。设f(x)是X的密度函数，f(x,y)是X、Y的联合密度函数，f(y|x)=f(x,y)/f(x)为给定X=x条件下Y的密度函数，则有

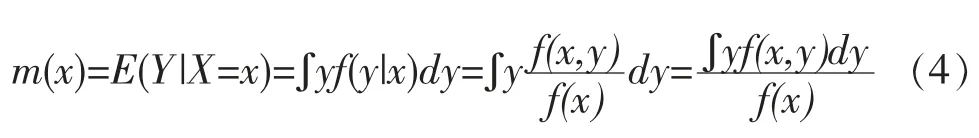
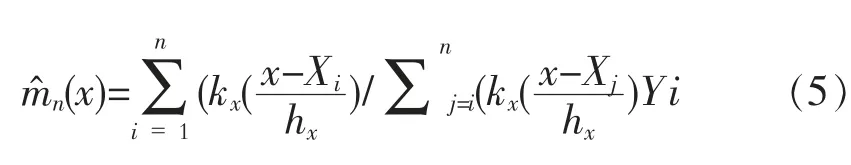
记hx=＾hn，权重，可以看出Wni(x)取值只与X的分布有关，称m＾n(x)为N-W估计。则Nadaraya-Watson核权函数回归估计表达式为：

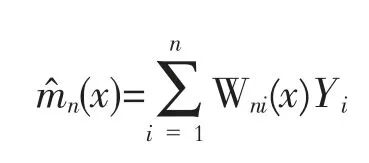
在此，核函数选择标准正态密度函数，

2.4 窗宽的选择

N-W核权函数回归估计的核心问题就是窗宽的选择。一方面窗宽越大,核估计的方差会变小,但同时核估计的偏差也会增大，导致密度曲线估计过于平滑，失去某些细节；另一方面,窗宽越小,核估计的偏差越小,但同时核估计的方差也会变大，导致密度曲线估计线欠平滑,产生不规则估计。因此，选择恰当的窗宽是N-W核权函数回归估计的关键。

实际应用中，选择窗宽的方法主要有经验法则（Rule of thumb）、直接插入法（direct plug in,DPI）、最小平方交叉实证法 （Least-squares crossvalidation,CV）和惩罚函数法（penalizing function）。

交叉实证法[6]是由Stone在1974年提出的，其基本思想是留下一个观测数据点作为估计的核实数据，而利用剩下的所有点来估计并建立模型，即在每个观测点x=Xi，首先，在样本中剔除观测值点(Xi,Yi)，用剩余的n-1个点在x=Xi处进行核估计：（其中,最后，在平均平方误差（ASE）值达到的最小条件下选择合适的窗宽hn，即使(Xi)]2最小的hn就是最佳的窗宽。本文试图采用最小平方交叉实证法（CV）和经验选择方法，根据拟合效果综合考虑优劣来选择合适的窗宽。

3 实证分析

3.1 样本的选定

选取1978-2013年我国财政收入与经济增长数据，来源于《2014年中国统计年鉴》。在具体变量选择上，财政收入使用财政收入指标，经济增长指标则采用国内生产总值。以1978年数据作为基期，算出财政收入增长率（FinanceRate）和GDP增长率（GDPRate）。从财政收入增长率和GDP增长率随时间变化的趋势图（图1）发现：二者各自随时间变化的规律不明显；在整体上，二者变化波动幅度不同且波动时效不一致，GDP增长率的变化总是快于财政收入增长率，但二者基本上是同向变动的，首先明确两者间确实存在某种关系。

用GDP增长率解释财政收入增长率，建立二者之间的参数回归方程与非参数回归方程，目的在于将两种方法进行对比。数据处理运用Eviews5.0和R软件。

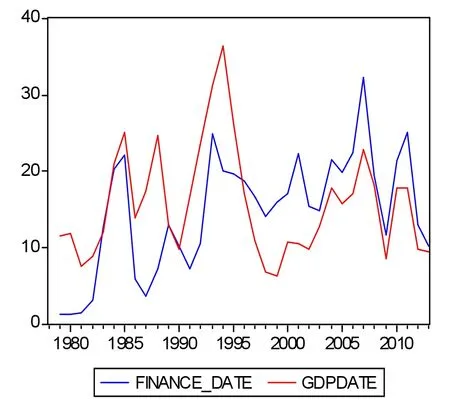
图1 财政收入增长率与GDP增长率时间变化趋势图

3.2 模型建立与求解

3.2.1 参数回归模型

首先，采用普通最小二乘法（OLS）建立国内生产总值增长率 （GDPRate） 与财政收入增长率（FinanceRate）的线性回归方程：

从方程系数的显著性πi 检验看，各项系数的πi值均大于临界值1.695，故系数是显著的；从方程整体显著性F检验看，其P-Value=0.007331＜0.05，应拒绝原假设，故方程的线性关系是显著成立的。但可决系数R2很小，说明方程拟合数据的程度不高，这也可以从二者的散点图（图2）看出。

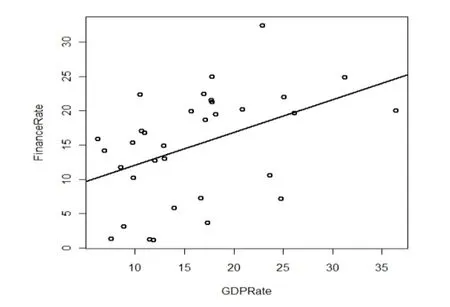
图2 财政收入增长率与GDP增长率的散点图及线性回归拟合

3.2.2 非参数回归N-W核估计模型

由图2可以看出财政收入增长率与GDP增长率之间不具有明确的线性关系，也没有确定的函数关系。故采用非参数估计方法建立财政收入与经济增长的回归模型，并将其与参数回归模型（6）进行比较。在（5）式中令x为GDP增长率，y为财政收入增长率。由此得到y关于x的N-W核权函数回归：

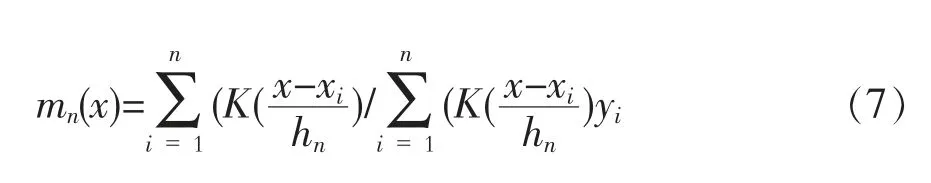
上式中核函数K(·)取标准正态密度函数。由交叉实证法得出的窗宽hn=3.045629，从图3可以看出此窗宽下的N-W核权函数回归大致能拟合分散的各点，但拟合曲线比较光滑，对某些细节解释不充分。根据散点图及经验方法，取窗宽为1.98和1.67，从图3看这两个窗宽值下的回归曲线拟合效果比交叉实证法得到的回归曲线效果要好，综合考虑后窗宽h=1.98。图4将线性回归直线与非参数回归所得的曲线放在同一坐标轴上，便于观察并得出结论。

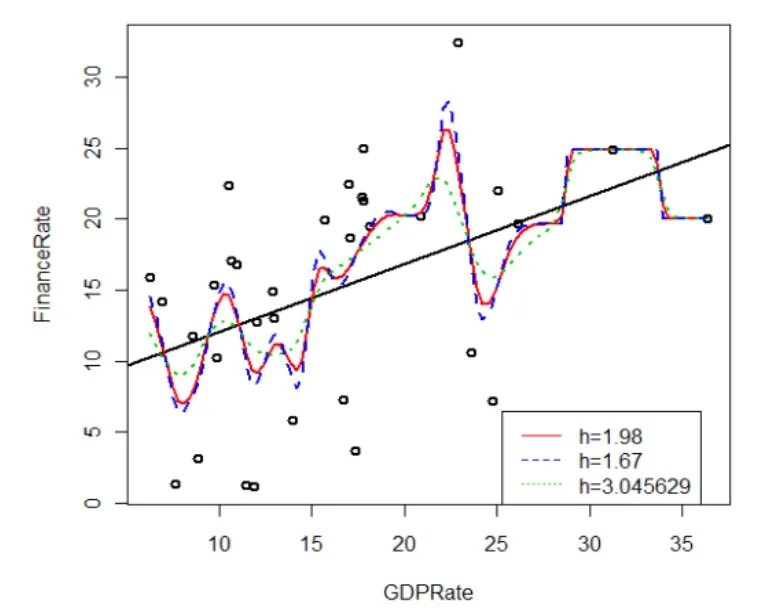
图3 非参数回归估计拟合图

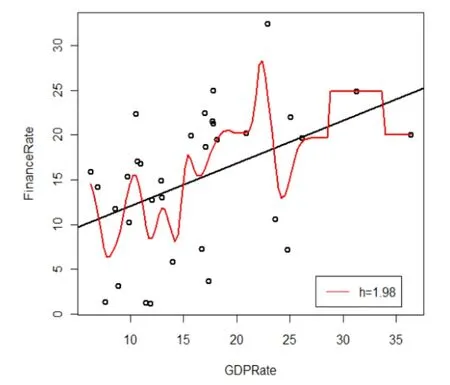
图4 线性回归与非线性回归效果比较图

4 结 论

通过对1978-2013年我国财政收入增长率与国内生产总值增长率数据的关系研究，可以发现二者同增同减，确实存在某种关系，但线性关系不明显。从线性回归模型和非参数回归模型的分析结果看出GDP增长率对财政收入增长率的影响在经济发展的不同时期有不同的特点，并非简单的线性模型能解释清楚，非参数回归模型的拟合效果要优于线性回归。这是因为用普通最小二乘法估计要符合严格的假定，而影响财政收入增长率波动性的因素很多。核估计的方法取决于数据本身及它们的参与程度，不需要严格的假设条件限制，故有更广泛的应用空间。

[1]李竹渝,鲁万波,龚金国.经济、金融计量学中的非参数估计技术[M].北京:科学出版社,2006:98-178.

[2]贾继花.财政收入与经济增长相关关系的分析[J].山东轻工业学院学报,2002(4):34-38.

[3]汤银才.R语言与统计分析[M]，北京：高等教育出版社,2008:229-271.

[4]吉亚辉,朱正取.甘肃省财政收入与经济增长的实证分析[J].西北师范大学学报,2009(3)：129-132.

[5]徐静,张瑛.非参数回归的核估计法在经济分析中的应用[J].科技信息,2008(25):189-190.

[6]李艳娟.核估计量与窗宽选择[J].辽宁工程技术大学学报,2006(6):478-480.