一种折射率传感的双芯光纤设计

刘旭安，陈达如，吴根柱，彭保进

(1.黄山学院 信息工程学院，安徽 黄山245041；2.浙江师范大学－浙江大学光学联合研究实验室，浙江 杭州310058)

1 引 言

在许多领域如化学、生物及光学应用等，折射率的大小对于分析介质材料的结构和特性起着重要的作用。基于折射率传感型的光纤传感器在过去十几年里由于其许多独特的性质如结构简单、高灵敏度、与光纤的兼容性、抗电磁干扰等等引起人们广泛的关注，相继提出了基于长周期光纤光栅的折射率传感型光纤传感器[1-3]、光纤布拉格光栅[4-6]、法布里-珀罗干涉仪[7-9]、表面等离子体[10-12]、光子晶体光纤[13-15]等。最近，几种基于微流控技术的折射率型光纤传感器被设计出来[16-18]，文献[18]还介绍了通过飞秒激光加工与刻蚀技术在光纤中引入微通道的相关工艺。

本文设计了一种新型双芯光纤，该折射率传感型光纤的横截面两个纤芯沿竖直方向对称分布，两纤芯中间位置引入一个小空气孔作为微通道。双芯光纤中两纤芯之间的模式耦合对中间空气孔的介质材料折射率具有高度的敏感性，因此，其中一个纤芯的输出光谱和中间空气孔的介质材料折射率具有一一对应关系，从而实现传感。这种折射率传感型的双芯光纤传感器具有成本低、结构简单的特点，因此具有许多潜在的优点。

2 光纤传感特性分析

本文提出的新型折射率型的双芯光纤传感器，其截面基本结构如图1所示。该型光纤两纤芯沿竖直方向对称分布，中间引入一个微型空气孔作为一个微通道。光纤的外直径为D，两纤芯分别为α 和β，其直径为d，之间的距离为H，中间微型空气孔的半径为r，该双芯光纤的长度为L。为了简化分析，规定光纤包层纯二氧化硅的折射率为1.45，空气折射率为1。光纤包层中二氧化硅和两纤芯之间的折射率差定在0.36%。在数值计算中，基本的参数设定为r=2μm,H=20μm,d=8.2μm,D=125μm，且光纤的外直径和纤芯直径大小和传统的单模光纤尺寸保持一致。本文采用全矢量有限元法来分析该型双芯光纤的传感特性。

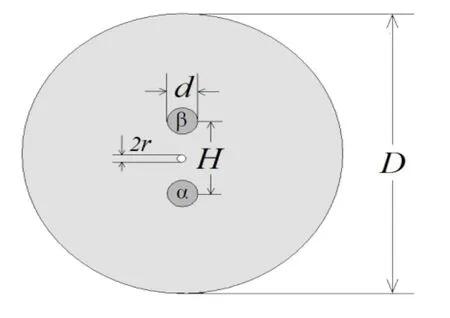
图1 新型双芯光纤截面结构示意图

由图可知，完全相同的两纤芯对称分布，形成两个相同的波导，由于两芯之间间距较小，因此两波导之间模式会发生耦合。如果在该光纤的输入端两纤芯α 和β 注入的光功率分别为1和0，根据传统模式耦合理论[19]，在长度为z的该型光纤的输出端，两纤芯α 和β 的输出光功率分别为

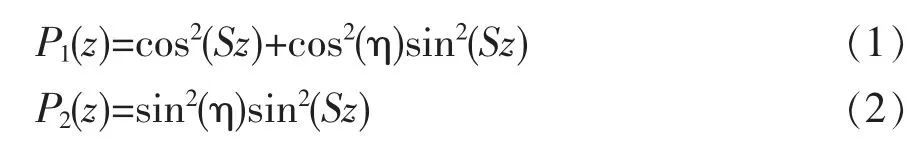
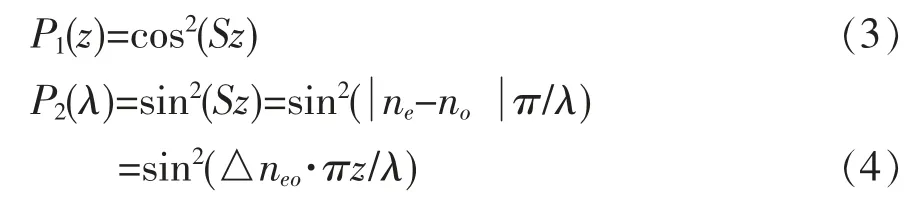
其中na和nb分别为该型光纤偶模和奇模的有效折射率，为有效折射率差。

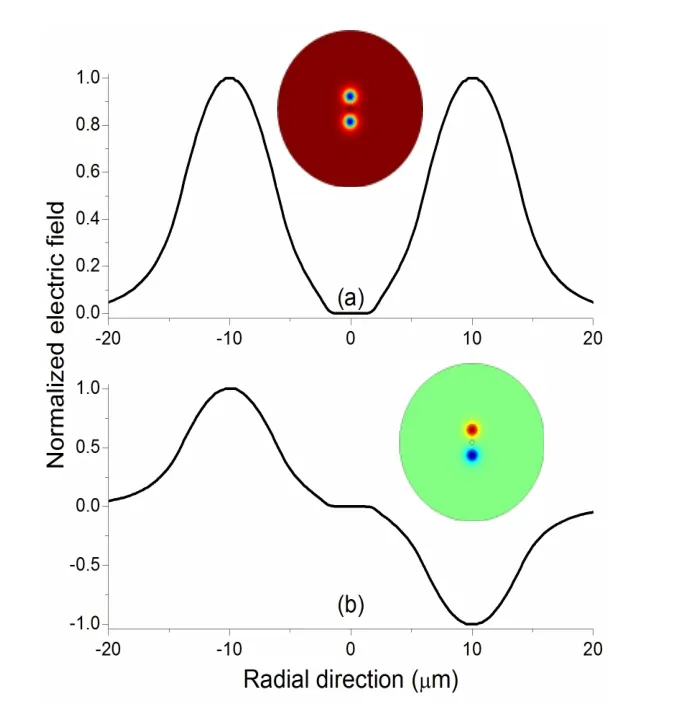
图2 光纤剖面电场模式分布图

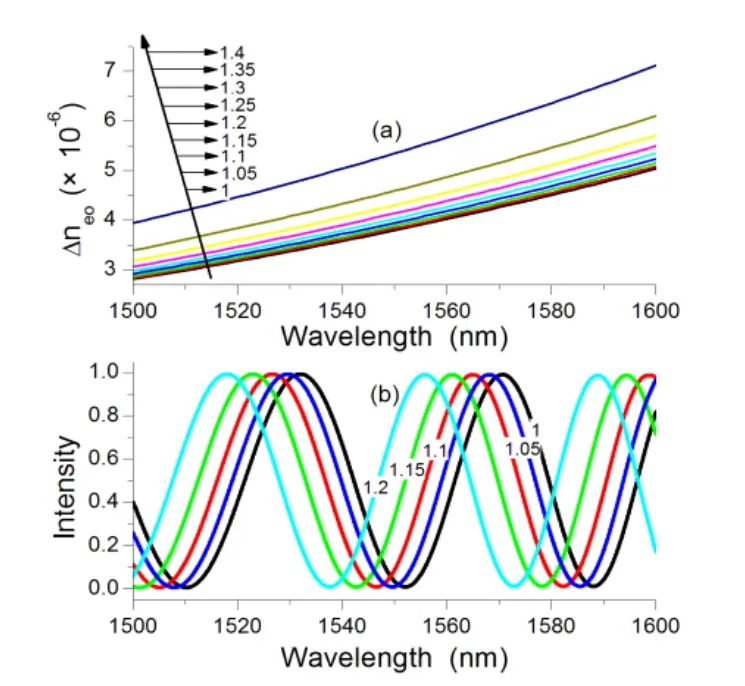
图3

3 计算结果

图2给出了该双芯光纤沿径向的电场分布曲线，图中插入部分为该双芯型光纤剖面电场分布图，其中图a为偶模时对应的电场分布，图b为奇模时对应的电场分布，基本参数为r=2μm,H=20μm,d=8.2μm和D=125μm，且工作波长为λ=1550nm，光纤中心小孔介质材料折射率为1。计算的有效折射率结果为ne=1.45223420107（偶模）和n0=1.45223040796（奇模），其中两纤芯之间的耦合长度Lc=π/(2S)=0.2043cm。可以看出有效折射率差△neo大小随工作波长和光纤中心小孔介质折射率的变化而变化。

图3（a）给出了该双芯光纤中间小孔介质材料折射率分别为1, 1.05, 1.1, 1.15, 1.2, 1.25, 1.3, 1.35,和1.4，工作波长在1500nm到1600nm范围内对应的折射率差△neo的变化曲线。由图可知，当光纤中心小孔介质折射率一定时，有效折射率差△neo随工作波长变化而缓慢变化，当光纤工作波长一定时，有效折射率差△neo随光纤中心孔介质折射率增大而增大。图3（b）给出了长度为1m且中间小孔介质材料折射率分别为1, 1.15, 1.2时的该型双芯光纤β的纤芯输出端的输出光功率谱P2(λ)的变化情况。从图中可以看出，由于该型双芯光纤β的纤芯输出端的输出光功率谱P2(λ)=sin2(△neo·πz/λ)，所以其输出光功率谱变化曲线类似于一个正弦函数，且随着光纤中心孔介质折射率增大，其输出光功率谱变化曲线向短波长方向移动。

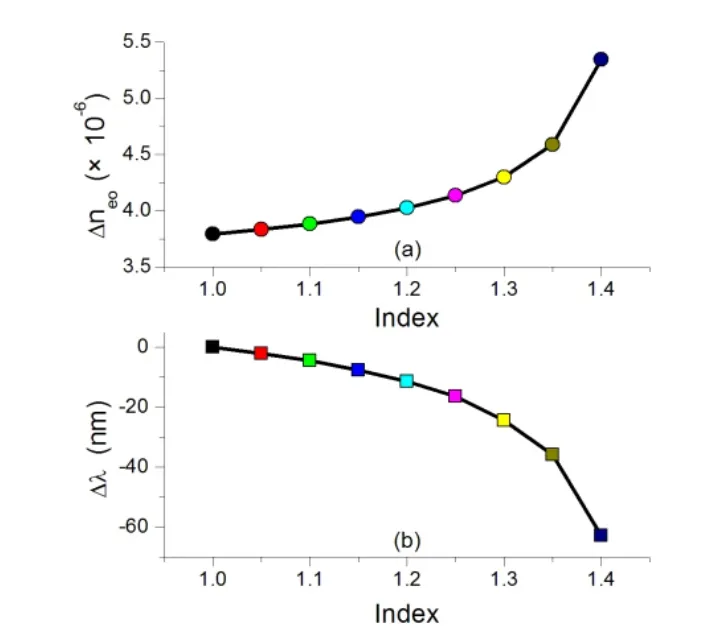
图4

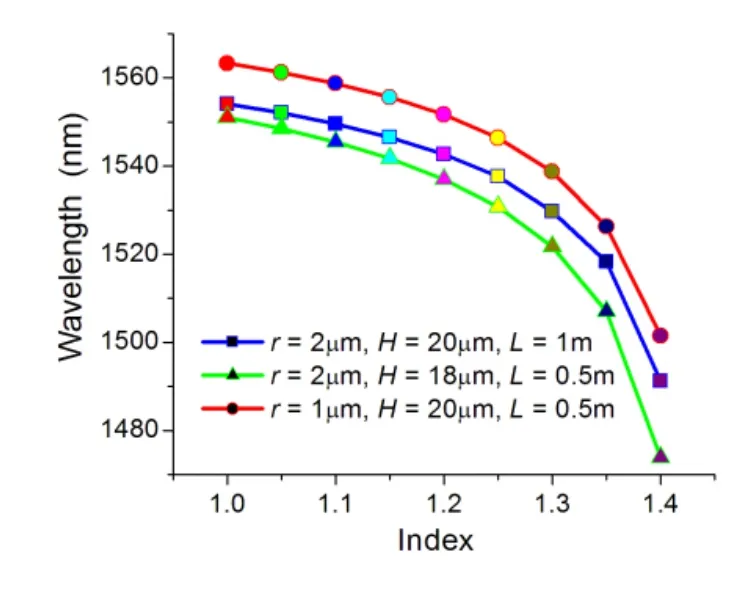
图5 在不同结构参数条件下，双芯型光纤β纤芯输出光谱随光纤中心小孔介质折射率变化的分布曲线

图4 （a） 给出了该双芯光纤在工作波长为1500 nm时折射率差△neo随光纤中心小孔介质折射率变化而变化的分布曲线。图4（b）给出了该双芯光纤在工作波长为1500nm时光纤β纤芯输出端的波长平移量△λ 随光纤中心小孔介质折射率变化的分布曲线。从图中可以看出，该双芯型光纤β纤芯输出光谱中波长平移与光纤中心小孔折射率之间具有一一变化对应关系，因此该型光纤可以制作出一种折射率传感型光纤传感器。计算结果显示，在光谱分析仪分辨率为1pm情况下，该型光纤传感器在光纤中心小孔介质折射率分别为1和1.4时对应的灵敏度为38.1207nm/RIU(2.623×10-5RIU)和1028.5464nm/RIU(9.7225×10-7RIU)，折射率传感范围为1到1.45。

图5给出了该双芯型光纤纤芯输出光谱随光纤中心小孔介质折射率变化的分布曲线。对应的结构参数分别为(r=2μm,H=20μm,d=8.2μm,D=125μm，L=1m),(r=2μm,H=20μm,d=8.2μm,D=125μm，L=0.5m)和(r=1μm,H=20μm,d=8.2μm,D=125μm，L=1m)。光纤中心小孔的尺寸大小可以根据具体的折射率传感应用而进行结构优化。

4 结 论

本文设计的新型双芯光纤，通过在光纤中心引入一个小孔，改变该孔介质折射率来影响两纤芯之间的模式耦合，从而使得光纤中心小孔折射率与光纤纤芯输出光谱之间具有一一对应关系，进而实现折射率传感。通过飞秒激光加工和刻蚀技术可以在该型光纤截面中心引入小孔。该折射率传感的双芯型光纤的传感原理主要是基于两纤芯的模式耦合理论。在一定的长度条件下，根据模式耦合理论，当偏振光入射到该光纤其中一个纤芯时，在光纤输出端的另一个纤芯上会输出类似正弦函数曲线的光谱分布。我们还给出了光纤中心小孔介质折射率与光纤输出光谱平移之间的一一对应关系，且研究了该折射率传感型双芯光纤的灵敏度和分辨率特性。

[1]PATRICK H J, KERSEY A D, BUCHOLTZ F.Analysis of the response of long period fiber gratings to external index of refraction[J].Lightwave Technol,1998, 16(9):1606-1612.

[2]KIM D W, SHEN Fa-bin, CHEN Xiao-pei, WANG Anbo.Simultaneous measurement of refractive index and temperature based on a reflection-mode long-period grating and an intrinsic Fabry–Perot interferometer sensor[J].Opt.Lett, 2005, 30(22):3000-3002.

[3]YANG Jian , YANG Li, XU Chang-qing, XU Cheng-lin,HUANG Wei-ping, LI Ying-fu.Long-period grating refractive index sensor with a modified cladding structure for large operational range and high sensitivityed on thinned and microstructure fiber Bragg grating [J].Appl.Opt,2006,45(24):6142-6147.

[4]IADICICCO A, CUSANO A, CUTOLO A, BERNINI R,GIORDANO M.Thinned fiber Bragg gratings as high sensitivity refractive index sensor [J].IEEE Photon.Technol.Lett,2004,16(4)：1149-1151.

[5]HUANG Xue-feng, CHEN Zhe-min, SHAO Li-yang, CEN Ke-fa, SHENG De-ren, CHEN Jun, ZHOU Hao.Design and characteristics of refractive index sensor based on thinned and microstructure fiber Bragg grating [J].Appl.Opt,2008, 47(4):504-511.

[6]FANG X, LIAO C R, WANG D N.Femtosecond laser fabricated fiber Bragg grating in microfiber for refractive index sensing[J].Opt.Lett,2011,35(7):1007-1009.

[7]RAN Zeng-ling, RAO Yun-jiang, ZHANG Jian,LIU Zhiwei,XU Bing.A miniature fiber -optic refractive -index sensor based on laser-machined Fabry–Perot interferometer tip[J].J.Lightwave Technol,2009,27(23):5426-5429.

[8]GONG Yuan, ZHAO Tian, RAO Yun-jiang, WU Yu,GUO Yu, A ray-transfer-matrix model for hybrid fiber Fabry-Perot sensor based on graded-index multimode fiber[J].Opt.Express ,2010, 18(15):15844-15852.

[9]ZHAO Jia-rong, HUANG Xu-guang, He Wei-xin, CHEN Ji-huan.High-resolution and temperature-insensitive fiber optic refractive index sensor based on fresnel reflection modulated by Fabry–Perot interference [J].J.Lightwave Technol, 2010,28(19):2799-2803.

[10]LI Yi,HARRIS E, CHEN Liang, BAO Xiao-yi, Application of spectrum differential integration method in an in-line fiber Mach-Zehnder refractive index sensor[J].Opt.Express,2010,18(8):8135-8143.

[11]SRIVASTAVA S K, VERMA R, K,GUPTA B D.Theoretical modeling of a localized surface plasmon resonance based intensity modulated fiber optic refractive index sensor[J].Appl.Opt,2009, 48(19):3796-3802.

[12]LU Yu-chun, HUANG Wei-ping, JIAN Shui-sheng.Influence of mode loss on the feasibility of grating-assisted optical fiber surface plasmon resonance refractive index sensors[J].J.Lightwave Technol,2009,27(21):4804-4808.

[13]WU Darran K C, KUHLMEY B T, EGGLETON B J.Ultrasensitive Photonic crystal fiber refractive index sensor.[J].Opt.Lett,2009,34(3):322-324.

[14]TOWN G E, WU Yuan, MCCOSKER R, BANG O, Microstructured optical fiber refractive index sensor[J].Opt.Let.,2010,35(6):856-858.

[15]HAN Ting-ting, LIU Yan-ge, WANG Zhi, ZOU Bing,TAI Bo-yin, LIU Bo.Avoided-crossing-based ultrasensitive photonic crystal fiber refractive index sensor[J].Opt.Lett,2010,35(12) :2061-2063.

[16]CATTANEO F, BALDWIN K, SHU Yang, KRUPENKINE T, RAMACHANDRAN S, ROGERS J A, Digitally tunable microfluidic optical fiber devices [J].J.Microelectromechan-ica Systems,2003, 12(6):908-912.

[17]HSIEH J, MACH P, CATTANEO F, SHU Yang, KRUPENKINE T, BALDWIN K, ROGERS J A.Tunable microfluidic optical-fiber devices based on electrowetting pumps and plastic microchannels[J].IEEE Photon.Technol.Lett,2003,15(1):81-83.

[18]Fu H, ZHOU K, SAFFARI P, MOU C, ZHANG L,He S, BENNION I.Microchanneled chirped fiber bragg grating formed by femtosecond laser -aided chemical etching for refractive index and temperature measurements[J].IEEE Photon.Technol.Lett,2008, 20(19):1609-1611.

[19]HUANG Wei-ping.Coupled-mode for optical waveguides:an overview [J].J.Opt.Soc.Am.A,1994,11(3):963-983.