大型散货船舶轴系冲击建模和仿真研究
袁皓月
(上海交通大学,上海 200240)
大型散货船舶轴系冲击建模和仿真研究
袁皓月
(上海交通大学,上海 200240)
为了更深入研究轴系的抗冲击特性以及动态特性,本文采用有限元数值分析计算方法,对主推进轴系进行垂向冲击的有限元建模,并利用该模型使用30g垂向冲击载荷为冲击输入条件,对一甲方单位提供的大型散货船舶图纸的船舶轴系的冲击响应特性进行仿真计算校核研究。
推进轴系 冲击计算 数值仿真
大型散货船舶推进轴系是一个典型的多阶梯多支撑连续弹性体,其作用是将主机发出的功率传递给螺旋桨,使螺旋桨产生推力并推进大型散货船舶前进或者后退,其推进轴系包括主机输出端推力轴承与螺旋桨之间的传动轴以及轴系附属设备。大型散货船舶经常航行在海况复杂多变的海域,会遭遇强风、强浪甚至是龙卷风台风等冲击,对大型散货船舶轴系的冲击特性有很大影响。故推进轴系的抗冲击能力直接关系到船舶动力系统的生存能力,因此,对大型散货船舶推进轴系进行抗冲击仿真计算就显得非常重要。本文在吸收和借鉴前人经验的基础上,对主推进轴系进行垂向冲击的有限元建模,并利用该模型使用30g垂向冲击载荷为冲击输入条件,对一甲方单位提供的大型散货船舶图纸的船舶轴系的冲击响应特性进行仿真计算校核研究。
1 轴系冲击的力学模型
本文中所述推进轴系连续系统是一个静不定结构,若采用连续系统模型求解冲击响应的解析解是非常困难的。在工程中对于推进轴系的冲击分析,通常采用有限个自由度模型,也就是把连续系统离散化为有限个集中质量,即有限个自由度的系统。
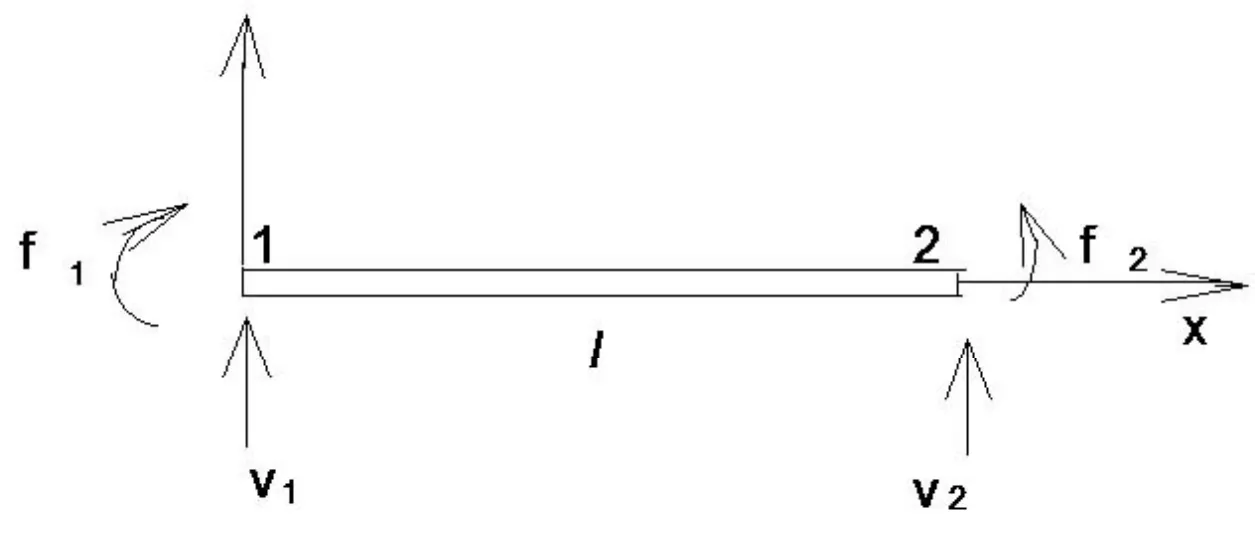
图1 梁单元示意图

图2-1 轴系建模示意图
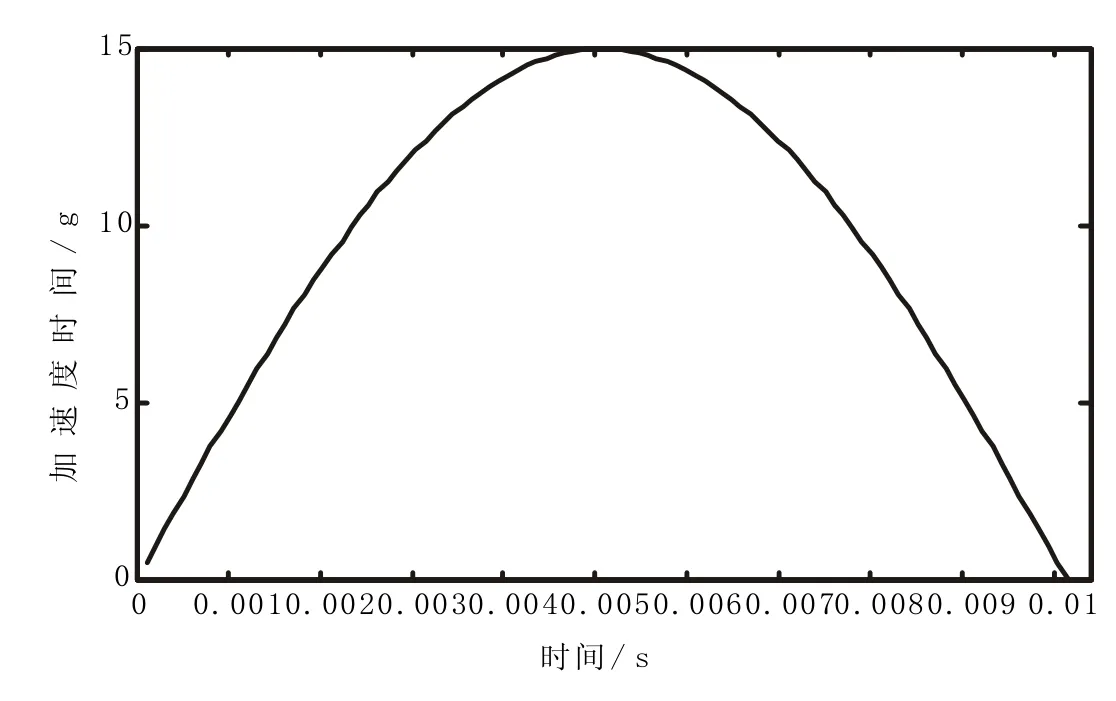
图2-3 横向冲击加速度历程图

图2-2 垂向冲击加速度历程图

图2-4 纵向冲击加速度历程图

图2-5 垂向加速度冲击下节点位移响应
1.1 主推进轴系垂向冲击的有限元建模
对弯曲振动的梁,如图1所示,它有两个结点,而每个结点处又有两个自由度,即横向位移ν和φ转角

故所选取位移假设需四个待定常数

由边界条件得

经推导,同样可得

则刚度矩阵为

式中,E为弹性模量,I为梁的截面惯性矩,l为单元的长度。
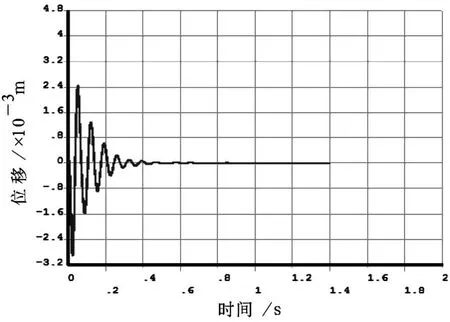
图2-6 横向加速度冲击下节点位移响应

图2-7 纵向加速度冲击下节点位移响应
同理,弯曲动能为

则质量一致矩阵为

为了把单元特性装配成结构特性,必须写出结构的动能和势能,它们为各单元动能和势能的累加,广义力可根据外力所作的虚功来求得。然后再利用拉格朗日方程得到整个结构的运动方程型式,即
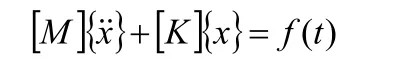
式中[M]、[K]分别为系统的质量和刚度矩阵;{x}是位移列向量;f(t)为冲击载荷列向量。一般而已,质量矩阵和刚度矩阵都具有带状形式。
1.2 轴系冲击位移响应数值仿真方法
轴系冲击响应计算主要包括两项内容:一是位移响应,二是力响应。 位移响应指系统内任意点处(或各单元)在冲击载荷激励下产生的位移响应,用以校核各关键部件是否超过所允许的位移限止;力响应指系统内各轴承座在冲击载荷激励下的冲击响应力,用来计算系统内实际部件的应力,进行强度校核。 在轴系承受垂向冲击响应计算中作以下假设:

表2-1 冲击加速度数值表

表2-2 船舶轴系不同冲击方向下的位移(mm)

表2-3 船舶轴系不同冲击方向下最大应力(MPa)

表2-4 船舶轴系支撑处最大位移值(mm)

表2-5 船舶轴系轴承支撑处应力值(MPa)
①轴系受到基础垂向冲击载荷为冲击速度(或冲击加速度);
②每阶模态受到的冲击速度(或冲击加速度)相等;
③轴系每个单元的冲击响应为各阶模态冲击响应的叠加;本计算取前十二阶模态;
我们用数值仿真方法计算轴系的冲击位移响应。数值仿真方法阐述如下:
对任何具有n自由度、受到基础加速度激励线性定常隔振系统,有n个耦合的运动微分方程,用矩阵形式可表示为

其中{x}是广义位移列向量,n x 1维;[M]、[C]、[K]分别为系统的质量、阻尼和刚度矩阵,nxn维;{p}为nx1维激励力向量系数;u˙˙为激励力幅值。


式中,[A]称为系统矩阵,2n x 2n维;[B]称为输入矩阵或控制矩阵,2nx2n维。
系统的输出量{Y}与状态向量{X}之间有如下关系

式中,{Y}为m x 1维向量,[C]称为系统的输出矩阵或观测矩阵,m x 2n维,而[D]则为m x 2维的矩阵。式(1-5)称为观察方程,表征了系统输出与状态之间的关系。令[C]= [I],[D]= [0],则{Y}={X}。
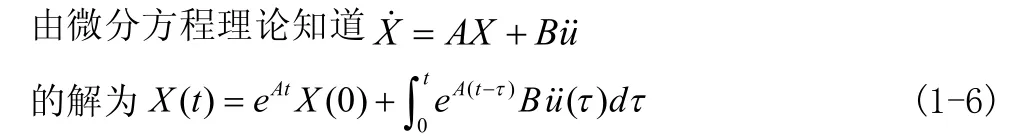
等式右边第一项表示初始条件引起的暂态过程,第二项表示控制作用(t)引起的系统状态变化过程。这个解也称为状态转移方程,我们主要应解决上式的算法问题。
把(1-6)式写成


于是上式进一步化为

如果把t = k h点的X(k) 作为初值来求X(k+1),则不难得到

当h及A一定时,F和G是常数,可以先算出来,则求微分方程解的问题化成了矩阵的四则运算:

只要知道A、B、F和G就可以求得任意输入u˙˙(k )下相应的X(k)。
2 冲击响应计算
2.1 冲击载荷输入
根据甲方单位大型散货船舶图纸提供的垂向冲击载荷为30g,横向冲击载荷按照垂向冲击载荷的0.5倍计算,即为15g;纵向冲击为垂向冲击的0.25倍,即7.5g。冲击脉宽为0.006s。
图2-1为艉管及隔舱密封处示意图,其中艉管密封有一处,隔舱密封有两处。
2.2 动力学计算
将冲击加速度波形按分步加载方式输入计算机,对轴系进行瞬态冲击响应计算,得到各截面动态剪力和弯矩,由此计算出相应的动态剪应力和动态弯应力。将其与静态下的应力进行综合后,得到危险截面的当量应力值。
图2-2,图2-3,图2-4分别为垂向、横向和纵向冲击时的加速度冲击波形及时间历程数据。
下面分别给出了30g加速度冲击下的计算结果,包括不同方向冲击下,轴系节点位移响应曲线、最大应力值、轴系重要位置处最大位移和应力值等。具体计算结果和分析过程如下。
2.3 30g加速度冲击计算结果
根据甲方单位所给冲击载荷,垂向冲击载荷为30g,横向冲击载荷为15g,纵向冲击载荷为7.5g,冲击脉宽为1s。(表2-1)
图2-5,图2-6,图2-7分别为垂向、横向和纵向加速度冲击时的1#节点的位移响应曲线。表2-2到表2-6分别给出了为垂向、横向和纵向加速度冲击时的节点最大位移和应力值。
由不同冲击方向最大位移表可以看出,垂向和横向冲击时,最大位移响应出现在节点86,即艉轴管轴承附近位置;纵向冲击时,最大位移响应出现在节点12,即后艉架轴承处。垂向冲击位移大于横向和纵向冲击。最大位移具体数值见表2-2。垂向冲击和横向冲击最大应力出现在节点69,即艉轴管轴承附近位置;纵向冲击时,最大应力出现在节点129,即2#中间轴承支撑处。最大应力具体数值见表2-3。船舶轴系支撑处最大位移及最大应力值分别如表2-4,表2-5所示。
2.4 许用冲击应力的确定
根据708所提供的轴系材料属性数据,其极限强度和屈服强度分别为:

根据规定,当结构不允许出现微小永久变形时,其许用应力取值如下:

2.5 结论
以上计算结果表明,轴系在不同冲击载荷作用下均满足强度要求。
3 结语
由于现实中推荐轴系尺寸大,附属设备多,无法准确完成实船冲击实验,本文采用有限元数值分析计算方法,对主推进轴系进行垂向冲击的有限元建模,并利用该模型对一甲方单位提供的大型散货船舶图纸的船舶轴系的冲击响应特性进行了仿真计算校核研究,为推进轴系抗冲击计算提供一种计算思路。

