基于分数阶微积分的裂纹转子系统非线性动力学特性研究

李志农，王海峰，肖尧先

（南昌航空大学无损检测技术教育部重点实验室，江西南昌330063）

基于分数阶微积分的裂纹转子系统非线性动力学特性研究

李志农，王海峰，肖尧先

（南昌航空大学无损检测技术教育部重点实验室，江西南昌330063）

在考虑非线性涡动的情况下，建立了分数阶阻尼裂纹转子系统的非线性动力学模型，并用龙格-库塔法和连分式Euler法对其进行了数值仿真。讨论了分数阶阶次、转子转速和裂纹深度对分数阶阻尼裂纹转子系统非线性动力学特性的影响。研究结果表明：对于具有分数阶特性的转子系统，采用分数阶来建立裂纹转子系统模型，能更好地揭示系统的非线性动力学特性；在相同的裂纹深度和相同的分数阶阶次下，随着转速比的增加，转子系统依次经历混沌、倍周期和周期运动；在相同的转速比和相同的分数阶阶次下，裂纹深度比较小时，引起的转子刚度变化量不大，一般不会出现复杂的分叉与混沌现象；随着裂纹深度的加深，转子的刚度减小，转子系统呈现复杂的振动特性，裂纹故障特征越来越明显，转子系统由单周期运动变换到倍周期运动，二倍频分量占主导地位，同时其他倍频分量也相继出现。这些有价值的结论对转子裂纹的故障诊断提供了参考。

机械学；分数阶微积分；裂纹转子；非线性动力学；非线性涡动；故障诊断

0 引言

转子是旋转机械中最重要的零件，在与转子有关的各种故障中，裂纹故障占相当的比例，转轴出现裂纹的潜在危害性与一般故障的危害性相比较要严重得多，它是一种后果严重、诊断困难、又十分隐蔽的常发性故障，裂纹的存在已成为影响设备安全运行的一大隐患。如何有效地诊断转子裂纹的存在，尤其是早期裂纹的出现，一直是当今研究的热点之一。国内外专家学者对裂纹故障的非线性特性进行了广泛深入的研究［1-10］。例如，文献［1］研究了谐波激励下的裂纹转子的动力学特性。文献［2］利用有限元分析方法分析了非对称裂纹转子的非线性动力学特性。文献［6］研究了含横向裂纹的Laval转子的非线性动力学特性。文献［7］采用理论方法、数字仿真和实验方法来研究发电厂旋转机械的裂纹监测。文献［8］利用非线性输出频率响应函数理论来对转子裂纹故障进行诊断。文献［9］利用B样条小波有限元对转子裂纹进行定量识别。文献［10］研究了基于模型的转子裂纹的辨识方法。然而，这些研究大部分都是在整数阶微积分基础上进行的，很少考虑分数阶微积分的裂纹转子系统。

由于许多物理系统因其特殊的材料和化学特性而展现出分数阶动力学行为，而实际系统大都是分数阶的，采用分数阶描述那些本身带有分数阶特性的对象时，能更好地揭示对象的本质特性及其行为。分数阶微积分是将通常意义下的整数阶微积分推广到任意阶，它包括了传统整数阶微积分运算，但又是整数阶微机分运算的拓展，与整数阶微积分相比较，具有以下优势:

1）分数阶微积分具有全局相关能较好地体现系统函数发展的历史依赖过程；而整数阶微积分具有局部性，不适合描述有历史依赖过程。

2）分数阶微积分模型克服了经典整数阶微分模型理论与实验结果吻合不好的严重缺点，使用较少几个参数就可获得很好的效果。

3）在描述复杂物理力学问题时，与非线性模型比较，分数阶模型的物理意义更清晰，表述更简洁。

目前，分数微积分在信号处理、图像处理、控制理论、电气工程和生物工程等领域获得了成功应用［11-22］。文献［11］研究表明，即使系统的所有个体具有整数阶动态特性，系统的整体动力学特性也可能是分数阶的。

近年来，也有一些学者把分数微积分应用到转子系统的非线性动力学分析中，曹军义等［17］在Duffing系统中研究了分数阶阻尼的阶数对系统的动力学特性的影响。文献［19-20］以Jeffcott转子模型为基础，建立了带有分数阶阻尼和横向呼吸裂纹故障的转子系统动力学模型，研究了阻尼的分数阶次，转速对裂纹转子系统动态特性的影响。

然而，在文献［19-20］中，裂纹开关函数模型只适合裂纹较浅的情况，当裂纹较深时，忽略了转轴刚度沿着裂纹前沿方向的变化。基于此，本文采用的裂纹模型把开闭浅裂纹模型和开闭深裂纹模型综合在一起，考虑了裂纹转轴沿裂纹前沿方向的刚度变化，在非线性涡动的情况下，建立分数阶阻尼转子系统动力学模型，分析了分数阶阶次、转子转速和裂纹深度对转子系统动力学特性的影响，为转子裂纹的故障诊断提供参考。

1 非线性涡动下的分数阶阻尼裂纹转子系统模型的建立

本文研究对象如图1所示是以两端简支、圆盘质量为m、长度为L、轴半径为R的无质量弹性圆轴所组成的含裂纹Jeffcott转子系统，考察的裂纹深度范围是0≤a/R≤1，其中a是裂纹深度，R是转轴半径。

设两端刚性支承带横向开闭裂纹Jeffcott转子的动力学模型为

式中:m为圆盘质量；kx、ky分别为裂纹轴沿x和y方向的刚度；kxy、kyx为x和y方向的耦合刚度；c为阻尼；e为不平衡偏心距；Ω为转速；β为不平衡量与裂纹法向的夹角。

图1 裂纹Jeffcott转子及裂纹轴横断面示意图Fig.1 Rotor model and cross-section of Jeffcott cracked shaft

考虑非线性涡动的影响，转子系统的刚度矩阵可表示为

式中:f（Φ）是描述裂纹开闭的函数，其形式与所采用的开闭裂纹模型有关；k为无裂纹转子刚度；Δkξ、Δkη分别为裂纹法向和切向刚度的变化量。根据Gasch［23］和Mayes等［24］的研究结果，这里浅裂纹（a/R＜0.5）时采用Gasch的铰链弹簧模型，深裂纹（a/R≥0.5）时采用Mayes等提出的改进裂纹模型。因此，裂纹开关函数f（Φ）［25］可表示为

式中:涡动角度为

由（4）式可知，Φ不仅与角速度Ω有关，而且与转子当前的涡动位置（x，y）有关，此裂纹开关函数模型考虑了转轴涡动对开闭裂纹的影响。

根据Hospital法则，对于可导函数f（t）可导出它的n（n∈N）阶导数为

引入Gamma函数，并将微分阶次从整数阶推广到分数阶，假设函数f（t）在区间［a，t］上有n+1阶导数，对于任意的实数r，利用有限记忆功能，则定义分数阶r微分为

在（6）式中统一表示了分数阶微分和积分，当r＞0时，表示分数阶微分；当r＜0时，表示分数阶积分。

若函数f（t）及其各阶导数的初值均为0，根据Riemann-Liouville定义，分数阶微积分表达式的Laplace变换为

采用Euler后项差分法，然后用连分式展开变换对分数阶微积分算子进行有理化近似，得到分数阶微积分的离散化模型为

式中:CFE｛·｝为连分式展开变换；p、q为阶次；Pp、Qq为p次和q次多项式。我们知道，传统的整数阶阻尼力是位移的1阶导数，而分数阶阻尼力是位移的分数阶导数，因而，整数阶阻尼是分数阶阻尼的特例。基于此，把整数阶阻尼力延拓到对位移的任意阶导数，就可得到分数阶阻尼力，相应的表达式［19］可表示为

考虑非线性涡动的情况下，分数阶阻尼裂纹转子系统的振动方程可表示为

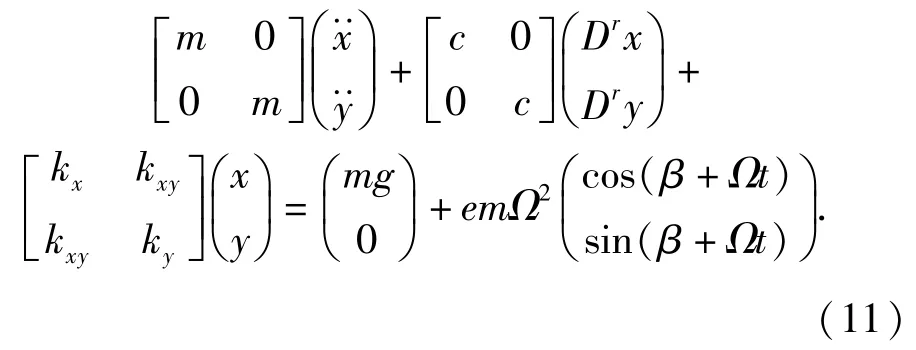
将（2）式、（3）式和（4）式代入（11）式，并将其无量纲化，分别令

式中:ωn为无裂纹轴1阶临界转速；C为重力下X方向的静变形。对（11）式进行归一化后，得到:

2 分数阶阻尼裂纹转子系统特性分析

采用4阶龙格-库塔法对方程（13）式进行数值积分，积分步长取为2π/200.计算时取阻尼比ζ= 0.01，无量纲不平衡量ε=0.1，并取初值｛x1，x2，x3，x4｝=｛0.1，0，0.1，0｝，不平衡量与裂纹法向之间的相位角β=0°.现来分析在非线性涡动的情况下，分数阶次、转速和裂纹深度对分数阶阻尼裂纹转子非线性动力学特性的影响。

首先，分析相同的裂纹深度和转速情况下，分数阶次对分数阶阻尼裂纹转子系统非线性动力学特性的影响。这里，在分数阶阻尼裂纹转子系统中，取裂纹深度a/R=0.7，转速比Ω/ωn=0.66.

随着分数阶阶次的变化，得到系统响应的分岔图如图2所示。由图2可知，随着分数阶阶次的改变，系统的振动特性受到了很大的影响。当分数阶阶次较小时，系统处于混沌运动。图3（a）给出了r=0.11的轴心轨迹和频谱图。由图3（a）可知，轴心轨迹图比较混乱，从其频谱图中可以看出，1×、3/2×和2×分量是主要成分，但是在0～3×之间出现许多频率成分，类似于噪声。当r＞0.4时，系统运动进入倍周期状态，图3（b）是r=0.6时系统的轴心轨迹图和频谱图，在频谱图中2×占主要成分，1×、3×相对较弱；轴心轨迹图呈双环型。当r=0.9时，系统仍为倍周期运动，频谱图中倍频成分相对于r=0.6时没有改变，但轴心轨迹图变为规则的内8字型。由于裂纹转子系统运动模型具有分数阶动力学特性，其振动特性受转速、裂纹深度的影响较大，在建立运动模型时，可以确定合适的分数阶阶次，来充分反映裂纹转子系统的振动特性，以达到诊断转子裂纹的最佳效果。

图2 分数阶阻尼阶次的分岔图Fig.2 Bifurcation diagram of fractional damping

其次，分析相同的裂纹深度和分数阶次情况下，转速对分数阶阻尼裂纹转子系统非线性动力学特性的影响。这里，分数阶次为r=0.7，裂纹深度为裂纹深度比a/R=0.6.

转速是影响转子系统动态特性的主要因素，当转速在转子的临界转速和亚临界转速附近时，会产生超谐共振、亚谐共振和参数共振现象，转轴的变形显著变大，涡动行为比较复杂，裂纹转子将呈现复杂的非线性行为。随着转速的变化，裂纹转子系统响应的分叉图如图4所示。图5给出了转速比Ω/ωn分别为0.328、0.51和1时的分数阶裂纹转子系统的轴心轨迹图和频谱图。

由图5可知，当转速比为0.328时，在分数阶裂纹转子系统，1×、2×和3×分量比较明显，4×、5×分量也能显示出来；在轨迹图中可以看出转子系统的轴心轨迹呈现复杂8字形的运动特性，非线性动力学特性反映明显。当裂纹转子系统的转速比为0.51时，转速处于转子系统主共振转速一半附近，轴心轨迹图变现为双环型，频谱图中出现1×、2×和3×分量，其中2×分量是主要成分。当转速比增大到1时，转子系统的轴心轨迹图近似为圆形，频谱图中1×占主要成分，2×分量较弱，此时系统为单周期运动。

最后，分析相同的转速和分数阶次情况下，裂纹深度对分数阶阻尼裂纹转子系统非线性动力学特性的影响。这里，分数阶次为r=0.7，转速比Ω/ωn=0.4.由于裂纹的出现，转子在运动的过程中受到重力和不平衡力的作用使裂纹作周期性的开闭运动，影响到转子刚度周期性变化，因此，裂纹转子的振动呈现出典型的非线性特性。图6给出了裂纹深度比为0.1、0.3和0.8时的分数阶阻尼裂纹转子系统的轴心轨迹和频谱图。

图3 分数阶阻尼裂纹转子轨迹图和频谱图（Ω/ωn=0.66，a/R=0.7）Fig.3 Trajectory and spectrum diagram of cracked rotor system with fractional damping（Ω/ωn=0.66，a/R=0.7）

图4 转子系统的分叉图（a/R=0.6，r=0.7）Fig.4 Bifurcation diagram of rotor system（a/R=0.6，r=0.7）

由图6可知，当裂纹较浅时，例如a/R=0.1，引起的转子刚度变化量不大，一般不会出现复杂的分叉与混沌现象，轴心轨迹图呈现椭圆型，在频谱图上，1×占主要成分，2×相对较弱。随着裂纹的加深，转子的刚度减小，裂纹故障特征越来越明显。当裂纹深度比为0.3时，转子系统的轴心轨迹从椭圆型变为外8字型，频谱图中，2×变大，其他高倍频也相继出现。当裂纹深度继续加深，裂纹转子的振动呈现复杂的振动特性，当裂纹深度比为0.8时，轴心轨迹从外8字型逐渐变为内8字型，频谱图中，1×、2×和3×是主要倍频分量，其中2×最大。

图5 分数阶阻尼裂纹转子轨迹图和频谱图（r=0.7，a/R=0.6）Fig.5 Trajectory and spectrum diagram of cracked rotor system with fractional damping（r=0.7，a/R=0.6）

为了验证上述分析的正确性，在Bently转子试验台上对含裂纹Jeffcott转子系统的非线性动力学特性进行了试验研究。为此定制了一根裂纹深度为直径25%的裂纹轴。图7是裂纹转子转速在2 050 r/min（Ω/ωn=0.5），裂纹相对深度a/R=0.5时，裂纹转子振动信号的轴心轨迹图和频谱图，转子系统的轴心轨迹图为典型的内8字型，频谱图中2×占主要成分，这与数值分析的结果相吻合。

3 结论

基于分数阶微积分的独特优势，本文将分数阶微积分引入到转子裂纹模型中，在非线性涡动情况下建立了分数阶阻尼裂纹转子系统动力学模型，与传统的整数阶转子裂纹非线性模型相比较，建立的模型更灵活，能更好地揭示裂纹转子系统的本质特性及其行为。并利用数值方法进行了仿真。讨论了分数阶阶次、转速和裂纹深度对裂纹转子系统的非线性振动特性的影响，得到了一些有价值的结论，可以作为诊断裂纹的重要依据。

图6 分数阶阻尼裂纹转子轨迹图和频谱图（Ω/ωn=0.4，r=0.7）Fig.6 Trajectory and spectrum diagram of cracked rotor system with fractional damping（Ω/ωn=0.4，r=0.7）

1）裂纹转子系统的阻尼具有分数阶特性，因此，采用分数阶动力学方程更能完全描述裂纹转子系统的动力学特性，只要确定合适的分数阶阶次，就能达到达到诊断转子裂纹的最佳效果。如何自适应地确定分数阶阶次，这是今后需要进一步值得研究的问题。

2）转速对分数阶阻尼的转子系统非线性动力学特性影响很大。在相同的裂纹深度和分数阶阶次下，随着转速变化，系统依次经历混沌运动、倍周期运动和单周期运动。1×、2×和3×等成分相继出现。转轴的变形显著变大，涡动行为比较复杂，裂纹转子将呈现复杂的非线性行为。

图7 裂纹转子轨迹图和频谱图Fig.7 Trajectory and spectrum diagram of cracked rotor system

3）对当裂纹较浅时，引起的转子刚度变化量不大，一般不会出现复杂的分叉与混沌现象；随着裂纹加深，转子刚度减小，振动呈现复杂的振动特性，裂纹故障特征越来越明显，轴心轨迹由依次由椭圆型变为外8字型，再变为内8字型。二倍频分量占据了主导地位，其他倍频分量也会相继出现。

（

）

［1］ Jun O S.Dynamic behavior analysis of cracked rotor based on harmonic motion［J］.Mechanical Systems and Signal Processing，2004，30（7）:186-203.

［2］ AL-Shudeifat M A.On the finite element modeling of the asymmetric cracked rotor［J］.Journal of Sound and Vibration，2013，332（11）:2795-2807.

［3］ AL-Shudeifat M A，Butcher E R，Stern C R.General harmonic balance solution of a cracked rotor-bearing-disk system for harmonic and sub-harmonic analysis:analytical and experimental approach［J］.International Journal of Engineering Science，2010，48（10）:921-935.

［4］ Bachschmid N，Pennacchi P，Tanzi E.A sensitivity analysis of vibrations in cracked turbogenerator units versus crack position and depth［J］.Mechanical Systems and Signal Processing，2010，24（3）: 844-859.

［5］ Sinou J J.Detection of cracks in rotor based on the 2×and 3× super-harmonic frequency components and the crack-unbalance interactions［J］.Numerical Simulation，2008，13（9）:2024-2040.

［6］ Robert G.Dynamic behaviour of the Laval rotor with a transverse crack［J］.Mechanical Systems and Signal Processing，2008，22（4）: 790-804.

［7］ Stoisser C M，S Audebert.A comprehensive theoretical，numerical and experimental approach for crack detection in power plant rotating machinery［J］.Mechanical Systems and Signal Processing，2008，22（4）:818-844.

［8］ 员险锋，李志农，林言丽.基于非线性输出频率响应函数的裂纹故障诊断方法研究［J］.机械强度，2013，35（2）:133-137. YUAN Xian-feng，LI Zhi-nong，LIN Yan-li.Rotor crack fault diagnosis method based on nonlinear output frequency response function［J］.Journal of Mechanical Strength，2013，35（2）:133-137.（in Chinese）

［9］ 陈雪峰，向家伟，董洪波，等.基于区间B样条小波有限元的转子裂纹定量识别［J］.机械工程学报，2007，43（3）:123-127. CHEN Xue-feng，XIANG Jia-wei，DONG Hong-bo，et al.Quantitative identification of rotor cracks based on finite element of B-spline wavelet on the interval［J］.Journal of Mechanical Engineering，2007，43（3）:123-127.（in Chinese）

［10］ Sekhar A S.Crack identification in a rotor system:a model-based approach［J］.Journal of Sound and Vibration，2004，270（4/ 5）:887-902.

［11］ Tenreiro M J A，Silva M F，Barbosa R S，et al.Some applications of fractional calculus in engineering［J］.Mathematical Problems in Engineering，2010，2010:1-34.

［12］ 周激流，蒲亦非，廖科.分数阶微积分原理及其在现代信号分析与处理中的应用［M］.北京:科学出版社，2010:86-99. ZHOU Ji-liu，PU Yi-fei，LIAO Ke.Research on application of fractional calculus to latest signal analysis and processing［M］. Bejing:Science Press，2010:86-99.（in Chinese）

［13］ Alberto S，Pietro C，Alberto C.Wave propagation in nonlocal elastic continua modelled by a fractional calculus approach［J］. Communications in Nonlinear Science and Numerical Simulation，2013，18（1）:63-74.

［14］ Richard L M.Fractional calculus models of complex dynamics in biological tissues［J］.Computers&Mathematics with Applications，2010，59（5）:1586-1593.

［15］ Roberto G，Federico P.Fractional calculus modelling for unsteady unidirectional flow of incompressible fluids with time-de-pendent viscosity［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17（12）:5073-5078.

［16］ 曹军义，曹秉刚.分数阶控制器离散方法的评估策略研究［J］.西安交通大学学报，2007，41（7）:842-846. CAO Jun-yi，CAO Bing-gang.Evaluation strategies of fractional order controllers discretization methods［J］.Journal of Xi'an Jiaotong University，2007，41（7）:842-846.（in Chinese）

［17］ 曹军义，谢航，蒋庄德.分数阶阻尼Duffing系统的非线性动力学特性［J］.西安交通大学学报，2009，43（3）:50-54. CAO Jun-yi，XIE Hang，JIANG Zhuang-de.Nonlinear dynamics of Duffing system with fractional order damping［J］.Journal of Xi'an Jiaotong University，2009，43（3）:50-54.（in Chinese）［18］ Rossikhin Y A，Shitikov M Y.Application of fractional calculus for dynamic problems of solid mechanics:novel trends and recent results［J］.Applided Mechanics Reviews，2010，63（1）:1-52.

［19］ 薛士明，曹军义，林京，等.分数阶阻尼裂纹转子的非线性动力学特性分析［J］.西安交通大学学报，2012，46（1）:76-80. XUE Shi-ming，CAO Jun-yi，LIN Jing，et al.Influences of fractional order damping on nonlinear dynamics of cracked rotor［J］. Journal of Xi'an Jiaotong University，2012，46（1）:76-80.（in Chinese）

［20］ Cao J，Xue S，Lin J，et al.Nonlinear dynamic analysis of a cracked rotor-bearing system with fractional order damping［J］. Journal of Computational and Nonlinear Dynamics，2013，8（3）: 21-34.

［21］ Cottone G，Paola M D，Butera S.Stochastic dynamics of nonlinear systems with a fractional power-law nonlinear term:the fractional calculus approach［J］.Probabilistic Engineering Mechanics，2011，26（1）:101-108.

［22］ 王在华，胡海岩.含分数阶导数阻尼的线性振动系统的稳定性［J］.中国科学:G辑，2009，39（10）:1495-1502. WANG Zai-hua，HU Hai-yan.Stability of a linear oscillator with damping force of the fractional-order derivative［J］.Science China:Ser G，2009，39（10）:1495-1502.（in Chinese）

［23］ Gasch R.A survey of the dynamic behaviour of a simple rotating shaft with a transverse crack［J］.Journal of Sound and Vibration，1993，160（2）:313-332.

［24］ Mayes I W，Davies W G R.A method of calculating the vibrational behaviour of coupled rotating shafts containing a transverse crack［C］//Proceedings of the 2nd International Conference on Vibrations in Rotating Machinery.Cambridge，UK:the Institution of Mechanical Engineers，1980:17-27.

［25］ 曾复，吴昭同，严拱标.裂纹转子的分岔与混沌特性分析［J］.振动与冲击，2000，19（1）:40-42. ZENG Fu，WU Zhao-tong，YAN Gong-biao.Analysis of bifurcation and chaos on a cracked rotor［J］.Journal of Vibration and Shock，2000，19（1）:40-42.（in Chinese）

Nonlinear Dynamic Characteristics of Cracked Rotor System Based on Fractional Order Calculus

LI Zhi-nong，WANG Hai-feng，XIAO Yao-xian
（Key Laboratory of Nondestructive Testing of Ministy of Education，Nanchang Hangkong University，Nanchang 330063，Jiangxi，China）

Nonlinear dynamics model of cracked rotor system with fractional order damping under the condition of nonlinear eddy is investigated and simulated by the Runge Kutta method and continued fractional expansion Euler method.The effects of derivative order，rotating speed ratio and crack depth on the nonlinear dynamic characteristics of cracker rotor system with fractional damping are discussed.The simulation results show that the model of cracked rotor system established with fractional order can reveal the nonlinear dynamics characteristics of a rotor system with fractional characteristics.In the same crack depth and fractional order，the rotor system gets chaotic，period-doubling and periodic motions as the factional order increases.In the same rotating speed ratio and fractional order，when the crack depth is small，the rotor system doesn't appear complex bifurcation and chaos phenomena.With the increase in crack depth，the stiffness of rotor system reduces and the rotor system presents the complex vibrationcharacteristics.The crack fault feature becomes more obvious.The rotor system gets from periodic motion to period-doubling motion.The double frequency component is dominant，and simultaneously other frequency multiplication component also appears.These valuable conclusions provide the important reference for the fault diagnosis of cracked rotor.

mechanics；fractional calculus；cracked rotor system；nonlinear dynamics；nonlinear eddy；fault diagnosis

TH113；O322

A

1000-1093（2015）09-1790-09

10.3969/j.issn.1000-1093.2015.09.026

2015-01-28

国家自然科学基金项目（51265039、51075372、50775208）

李志农（1966—），男，教授，博士。E-mail:lizhinong@tsinghua.org.cn