舰艇摇摆下射界动态变化对武器目标分配的影响

余戌曈，吴玲，卢发兴

（海军工程大学电子工程学院，湖北武汉430033）

舰艇摇摆下射界动态变化对武器目标分配的影响

余戌曈，吴玲，卢发兴

（海军工程大学电子工程学院，湖北武汉430033）

研究了舰艇摇摆下武器射界的动态变化，及其对武器目标分配问题的影响。在甲板面参考系建立目标运动模型，将舰艇摇摆转换为目标的相对运动。定义舰艇最大摇摆误差角来表征舰艇摇摆下目标位置与武器射界之间的关系，并基于该角度值得到摇摆情况下的武器目标分配规则。通过算例计算分析了轻度模式、中度模式、重度模式、重度损伤模式4种不同舰艇摇摆模式下的最大摇摆误差角。舰艇最大摇摆误差角可作为摇摆条件下武器目标分配的依据，同时可为舰船设计中武器水平射界重叠区的设计提供参考。

兵器科学与技术；舰艇摇摆；射界；舰艇摇摆误差角；武器目标分配

0 引言

射界是舰载武器的固有性质，是在保证舰艇人员和设备安全的前提下，武器能够射击的方位角和高低角的范围［1］。在作战过程中，目标分配时必须考虑武器射界，不在射界内的目标不能分配给该武器打击。舰艇在海面上活动时，受风浪等因素的影响进行周期性的摇摆，安装在舰艇上的武器随舰艇摆动，使其射界也随之动态变化。舰艇摇摆对目标跟踪拦截过程中的传感器配准融合［2］、目标分配、火控解算［3-4］、武器发射［5］等均会产生较大影响，但目前对目标分配的影响尚未深入研究。本文通过建立甲板面参考系下的目标运动模型，将复杂的射界变化问题转换为目标的相对运动，并提出舰艇摇摆误差角的概念，由此研究舰艇摇摆所产生的武器射界动态变化对武器目标分配问题的影响，同时为解决舰艇摇摆下的目标分配问题和舰载武器射界重叠区的设计提供依据。

1 甲板面参考系下目标运动模型

由于舰载武器处于狭小甲板上且周围有许多障碍物，所以武器射界是一个不规则区域，在考虑舰艇摇摆后对其研究过于复杂。为了简化研究且不改变问题的本质，本文在甲板面参考系下，研究舰载武器射界与飞抵我舰的目标之间的相对位置关系，此时受舰艇摇摆的影响，武器可视为静止不动，而目标的相对运动轨迹与稳定舰艇参考系下的轨迹产生了偏离，从而将射界变化问题转换为目标在甲板面参考系下的相对运动。

舰艇在水面上受风浪等影响而产生的运动的形式有横摇、纵摇、艏摇、纵荡、横荡、垂荡等，其中横摇和纵摇对舰艇的影响最大，故本文只考虑舰艇纵摇角ψ和横摇角θb［6］.假定舰艇静止且位于原点，舰艏朝向正北，舰艇航向CW=0，航速vW=0，以舰艇为参考系原点，建立稳定舰艇参考系。稳定舰艇参考系的原点是舰艇的摇摆中心，它的3条参考轴与舰艇不固连，y轴为舰艇纵轴在水平面上的投影线（即航向线），指向舰艏方向；x轴在水平面内与y轴垂直，指向舰艇右舷；z轴垂直水平面，指向天顶。由于x轴、y轴、z轴不随舰艇摇摆而改变指向，因此是稳定的。来袭目标在稳定舰艇参考系下的实时位置［7］可描述为

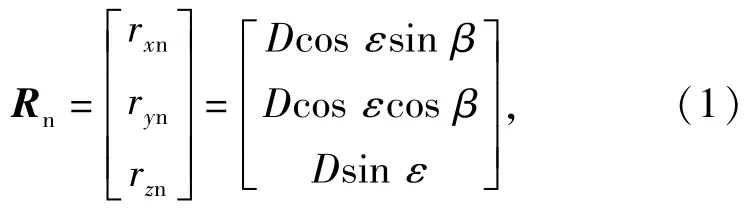
式中:Rn为目标位置；rxn、ryn、rzn分别为在x轴、y轴和z轴方向上的分量；D为目标与我舰距离；β为目标的方位角；ε为目标的高低角。

考虑舰艇摇摆，以舰艇为参考系原点，建立甲板面参考系。甲板参考系的原点是舰艇的摇摆中心，它的3条参考轴与舰艇相固连，y轴为舰艇纵轴（即舰的艏艉线）相平行，指向舰艏方向；x轴与舰横轴相平行，指向舰的右舷；x轴与y轴构成的平面称为甲板面，z轴垂直甲板面指向天顶。它会随着舰艇移动、摇摆和升沉，所以是不稳定的。根据坐标由稳定舰艇参考系到甲板面参考系变换公式［7］，该目标在甲板面参考系下的位置点可描述为

式中:Rb=［rxb，ryb，rzb］T为甲板面参考系下目标位置；为舰艇航向变换矩阵，由于CW=0，所以，E为单位矩阵；为舰艇纵摇变换矩阵；为舰艇横摇变换矩阵；ψ为舰艇纵摇角；θb为舰艇横摇角。

由（1）式和（2）式可知，在甲板面参考系下，目标运动轨迹任一点的位置可以由目标的初始位置，即初始距离D0、初始方位角β0、初始高低角ε0及目标速度vm、目标航向Cm、目标俯冲角λ和舰艇摇摆所决定。即目标全航路位置点集Rb（t）可表示为

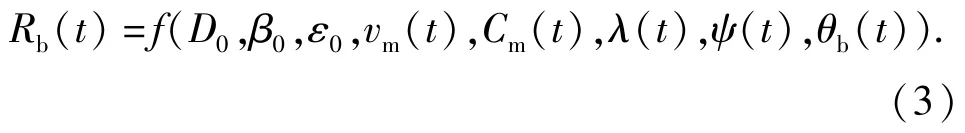
由此就可以研究在稳定舰艇参考系下任意位置的目标，其在甲板面参考系下所对应的位置。例如，当目标在高低角ε=20°，方位角ω=0°，距离我舰D=10 000 m处，零航路捷径匀速直线俯冲飞抵我舰，我舰纵横摇以中度模式进行摇摆，则在稳定舰艇参考系下和在甲板面参考系下的其飞行轨迹如图1和图2所示。

图1 目标航路侧视图Fig.1 Side view of target route

2 舰艇摇摆误差角

舰艇摇摆造成目标在甲板面参考系和稳定舰艇参考系下的位置在方位与高低上发生偏移。分别定义舰艇摇摆方位误差角和舰艇摇摆高低误差角来描述其在方位角与高低角上的偏移。如图3和图4所示，我舰位置为点O；在甲板面参考系Oxyz下，目标的位置为Rb，ORb为武器瞄准线；在舰艇稳定参考系下，目标的位置为点Rn，ORn为武器瞄准线，β为目标方位角；Rn、Rb与我舰距离均为d.

图2 目标航路俯视图Fig.2 Vertical view of target route

图3 舰艇摇摆方位误差角Fig.3 Ship swaying azimuth error angle

在甲板面Oxy上定义舰艇摇摆误差半角:

式中:规定Rb在目标飞行方向的左侧时ηβb为负，反之为正。该角度可反映舰艇摇摆下目标方位角偏移。

图4 舰艇摇摆高低误差角Fig.4 Ship swaying elevation error angle

图4中，Ox′轴为武器的俯仰轴，Oy′轴为武器瞄准轴［7］，点Rb在该轴上。以瞄准垂面Oy′z作为参考面。点为点Rn在Oy′z上的投影。将点Rb与直线之间的垂直距离定义为舰艇摇摆高低误差距离lε，即目标因舰艇摇摆造成在瞄准垂面Oy′z上与原目标瞄准线上的距离偏差:

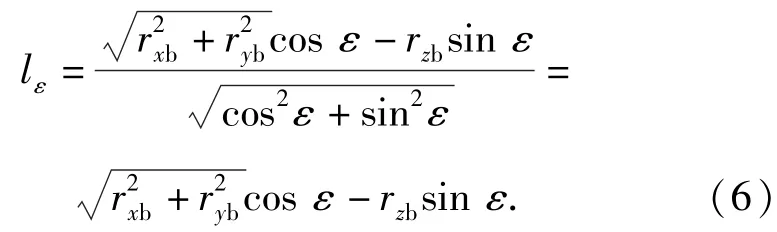
在瞄准垂面Oy′z上定义舰艇摇摆高低误差半角:

式中:规定Rb在目标飞行方向的下方时ηεb为负，反之为正。该角度可反映舰艇摇摆下目标高低角偏移。

定义舰艇摇摆下最大方位误差角ηβ和最大高低误差角ηε:

它们是衡量目标在全航路上因舰艇摇摆所造成方位角和高低角偏移程度的指标，即目标在舰艇摇摆条件下飞抵我舰的相对航路均以原航路为中心，方位上在ηβ角度范围内，高低上在ηε角度范围内。

由（1）式、（2）式、（4）式～（9）式可知，最大舰艇摇摆误差角ηβ和ηε的大小只由舰艇纵摇角、横摇角和目标高低角、方位角所决定，与目标距离、速度、航向、俯冲角等因素无关，即

3 舰艇摇摆对目标分配的影响

由于武器高低射角一般较大，舰艇摇摆对目标分配问题的影响主要存在水平方向上，故本文只分析方位角上舰艇摇摆对目标分配的影响。舰艇防空武器都有各自的射界，其水平射界一般由远近界和水平射角决定，舰艇摇摆造成射界动态变化对目标分配的影响主要发生在目标处于射界边缘位置。如图5所示，武器A的射角为σA，武器B的射角为σB，两武器射角的重叠角为σAB，即σAB=σA∩σB.目标在该两武器射界交界处飞抵我舰，有如下3种情形:

1）舰艇摇摆使得目标的飞行轨迹未超出两武器的射界重叠区，即最大摇摆方位误差角ηβ⊂σAB，则武器目标分配不受舰艇摇摆影响，如图5（a）所示。

2）目标的飞行轨迹只完全落在一个武器的射界内，即ηβ⊂σA且ηβ⊄σAB或ηβ⊂σB且ηβ⊄σAB，则选择相应的武器打击目标如图5（b）所示。

3）目标的飞行轨迹均不完全落在某一武器射界内，即ηβ⊃σAB，则应同时使用这两个武器打击该目标如图5（c）所示。

上述第3种情形下，可能出现两武器的火力交叉或弹药浪费，应尽量避免，因此在舰船设计时也可根据典型海况和目标运动态势计算出ηβ，并以此作为武器水平射界重叠区的参考角，即σAB≥ηβ.一般可在5级海况下计算相应ηβ作为射界重叠区参考角。

图5 舰艇摇摆方位误差角与武器射界重叠角Fig.5 Ship swaying azimuth error angles and firing overlap zone angles

4 算例分析

根据不同的舰艇航行环境，分4种模式模拟舰艇的纵横摇状态，如表1所示。

表1 模拟舰艇纵摇和横摇状态参数表Tab.1 State parameters of simulated longitudinal and lateral swaying of ship

舰艇纵摇ψ和横摇θb分别模拟为

式中:ψmax为纵摇最大幅度；Tψ为纵摇周期；θbmax为横摇最大幅度；Tθb为横摇周期；t为摇摆时间（s）。所有纵摇和横摇在开始时刻都是0°，纵摇、横摇均先行向符号为正的方向摇摆；舰艏向上，舰艉向下时纵摇为正；左舷高，右舷低时横摇为正。

轻度模式下，目标方位角β取不同值时，仿真获得的最大摇摆方位误差角ηβ与目标高低角ε关系如图6所示，其中目标高低角大于80°时最大摇摆方位误差角陡增，此时摇摆对目标分配的影响严重。在其他3种模式下的类似仿真表明，摇摆越剧烈，造成误差角陡增的目标高低角越小，即摇摆程度越大，能可靠分配的目标的高低角越小。

图6 不同目标方位角下最大摇摆方位误差角与目标高低角的关系Fig.6 Relationship between maximum ship swaying azimuth error angle and target elevation angle

目标方位角β取0°～360°，目标高低角ε分别取10°、20°、30°、40°、50°、60°时，舰艇在不同的摇摆模式下，最大摇摆方位误差角ηβ的函数由（1）式，（2）式，（5）式和（8）式计算得到，如图7～图10所示。

图7 轻度模式下最大摇摆方位误差角Fig.7 Maximum ship swaying azimuth error angle in mild sway mode

由图7～图10可见，目标从左右舷方向飞抵我舰时最大摇摆误差角较小，而从舰艏艉方向飞抵时误差角相对较大，这是由于舰艇的横摇幅度一般明显大于纵摇，而左右舷的摇摆误差角受纵摇影响明显，舰艏艉的误差角受横摇影响明显。

在图7～图10的仿真中，目标高低角ε取60°时，4种不同模式下的最大摇摆方位误差角取值如表2所示。

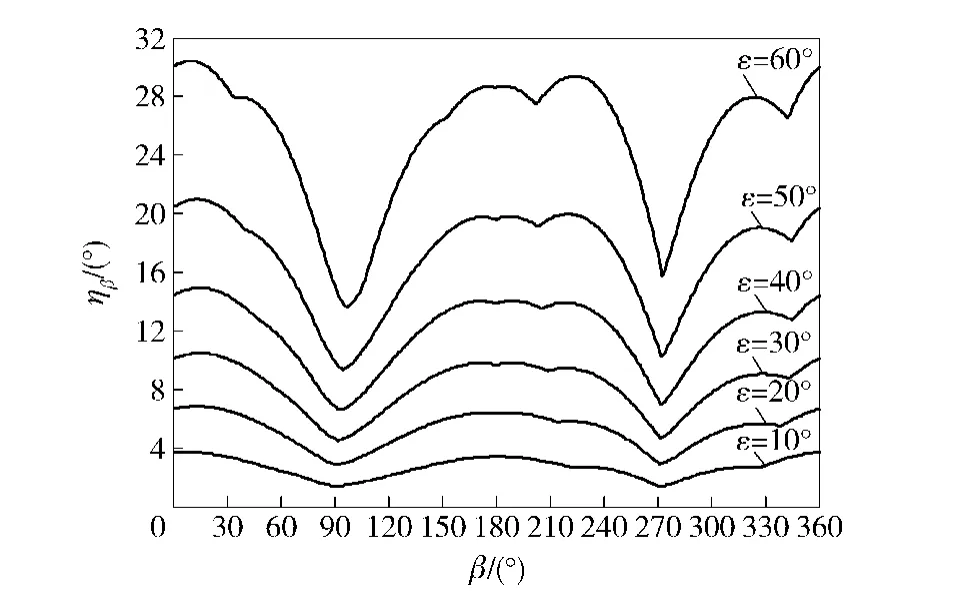
图8 中度模式下最大摇摆方位误差角Fig.8 Maximum ship swaying azimuth error angle in moderate sway mode

图9 重度模式下最大摇摆方位误差角Fig.9 Maximum ship swaying azimuth error angle in severe sway mode

图10 重度损伤模式下最大摇摆方位误差角Fig.10 Maximum ship swaying azimuth error angle in severe damage mode

表2 4种模式下的最大摇摆方位误差角Tab.2 Maximum ship swaying azimuth error angle in 4 modes

根据仿真结果，可得如下结论:

1）舰艇摇摆使武器的射界发生改变，并相应对武器目标分配问题产生影响；摇摆越剧烈，对分配的影响越大。

2）舰艇最大摇摆误差角只由舰艇纵摇角、横摇角和目标高低角、方位角所决定，它可以有效衡量目标位置与动态变化的武器射界之间的关系，并作为舰艇摇摆下武器目标分配的依据。

3）典型摇摆模式和目标运动态势下的最大摇摆误差角可作为舰船设计时武器水平射界重叠区的参考角。

5 结论

本文在我舰地理位置静止，敌来袭空中目标保持一定的航速、航向的前提下，研究了目标在甲板面参考系下的运动模型，提出了舰艇摇摆误差角，分析了该角度与舰艇纵摇和横摇、目标方位角、高低角之间的关系，并将舰艇摇摆误差角作为舰艇摇摆下武器目标分配的依据，同时为舰载武器水平射界重叠区的设计提供参考。该结论亦可以对舰艇及目标动态变化的情形提供理论依据基础。

（

）

［1］ 张平.某舰安全射界设计综述［J］.舰船科学技术，1996（2）: 13-17. ZHANG Ping.Safety firing-zone design summarization of ship［J］. Ship Science and Technology，1996（2）:13-17.（in Chinese）

［2］ Zhang P X，WANG H Y，Liu C B，et al.An improved time synchronization algorithm based on continuous observation and time warp estimate［C］//3nd International Conference on Computer and Network Technology.Taiyuan，China:IEEE，2011:241-243.

［3］ 朱利锋，鲍其莲.船舶摇摆运动对船载炮射击的影响［J］.火力与指挥控制，2005，30（2）:91-94. ZHU Li-feng，BAO Qi-lian.Effects of ship swaying motion on shipbased cannon firing［J］.Fire Control and Command Control，2005，30（2）:91-94（in Chinese）

［4］ 张龙杰，谢晓方，孙涛，等.舰艇摇摆对小口径舰炮射击精度的影响分析［J］.火炮发射与控制学报，2013（1）:11-15. ZHANG Long-jie，XIE Xiao-fang，SUN Tao，et al.Analysis about influence of warship rocking on firing accuracy of small caliber naval gun［J］.Journal of Gun Launch&Control，2013（1）:11-15.（in Chinese）

［5］ 李翔，毕世华，陈阵.舰船摇摆对舰载火箭初始扰动影响的多因素分析［J］.北京理工大学学报，2011，31（3）:253-257. LI Xiang，BI Shi-hua，CHEN Zhen.Multivariate analysis on initial disturbances effect of ship launched rocket excited by ship swaying motion［J］.Transactions of Beijing Institute of Technology，2011，31（3）:253-257.（in Chinese）

［6］ 李积德.船舶耐波性［M］.哈尔滨:哈尔滨工程大学出版社，2007:3-4. LI Ji-de.Ship seakeeping［M］.Harbin:Harbin Engineering University Press，2007:3-4.（in Chinese）

［7］ 王航宇，王士杰，李鹏.舰载火控原理［M］.北京:国防工业出版社，2006:9-26. WANG Hang-yu，WANG Shi-jie，LI Peng.Shipborne fire control theory［M］.Beijing:National Defense Industry Press，2006:9-26.（in Chinese）

The Influence of Dynamically Changing Firing Zone on Weapon-target Assignment under Ship Swaying

YU Xu-tong，WU Ling，LU Fa-xing
（College of Electronic Engineering，Naval University of Engineering，Wuhan 430033，Hubei，China）

The dynamic change of firing zone under ship swaying and its effect on the weapon-target assignment（WTA）are studied.A target moving model in the deck reference system is built，and a ship swaying error angle（SSEA）model is proposed，which can illustrate the relationship between the target position and the firing zone under swaying.The rules of WTA under swaying are drawn with the SSEA as an evaluation index.The maximum SSEAs in four sway modes are computed via simulations.The results show that the maximum SSEA can be used as a valid basis for WTA under the ship swaying and provides a reference for designing the firing overlap zone.

ordnance science and technology；ship swaying；firing zone；ship swaying error angle；weapon-target assignment

TJ391

A

1000-1093（2015）09-1819-06

10.3969/j.issn.1000-1093.2015.09.030

2015-01-19

总装备部预先研究基金项目（9140A06040111JB1113）；湖北省自然科学基金项目（2012FFC129）

余戌曈（1990—），男，硕士研究生。E-mail:yxtmcy0217@qq.com；吴玲（1976—），女，副教授，硕士生导师。E-mail:wuling@sina.cn