基于粒子群优化的再入可达区计算方法研究

赵江，周锐

（北京航空航天大学自动化科学与电气工程学院，北京100191）

基于粒子群优化的再入可达区计算方法研究

赵江，周锐

（北京航空航天大学自动化科学与电气工程学院，北京100191）

针对升力式高超声速飞行器再入可达区计算问题，提出了一种粒子群优化（PSO）和倾侧角反转相结合的混合求解方案。为了减小待优化变量的搜寻空间，设计了一种参数化的倾侧角剖面，利用约束PSO算法求解满足再入过程约束和末端约束的最优滑翔轨迹。通过倾侧角正向和逆向反转逻辑直接生成倾侧角指令集合，进而实现高超声速飞行器再入可达区的快速估算。高升阻比再入滑翔飞行器CAV-H仿真实例表明，该混合优化求解方案易于实现且无需预估参数初值，具有良好的可操作性。

兵器科学与技术；粒子群优化；再入可达区；高超声速飞行器；倾侧角反转逻辑

0 引言

高超声速飞行器的再入环境复杂，其制导和控制性能受到动力学系统的强扰动性和大气模型参数的不确定性等诸多因素的制约。因而，高超声速再入滑翔技术已经成为各国航空航天领域研究的重要问题［1-3］。再入可达区又称再入覆盖区，是指再入滑翔飞行器以某一初始条件再入地球表面时，能够获得着陆或交班状态的区域范围，是评估再入滑翔飞行器覆盖能力的重要性能指标。因此，开展再入可达区计算方法研究，探索多约束条件对目标覆盖区域的影响机理，能够有效地优化远程攻击方案设计，提升再入滑翔飞行器的突防和生存能力［4］。

文献［5］利用准平衡滑翔条件，结合初始俯冲策略确定了再入攻角的设计空间，并将其应用于再入可达区的优化问题。文献［6-7］将再入飞行器的最大航程问题转换为搜寻虚拟目标的最短路径问题，通过合理设计倾侧角反馈控制率，求解满足终端约束的最短路径集合，进而实现目标覆盖区域的精确计算。文献［8］将再入可达区问题转化成一系列的轨迹优化问题，采用序列梯度修复算法求解满足过程约束的再入可达区。文献［9］针对可重复使用运载器的覆盖区域问题，结合全局和局部优化算法的特点，设计了遗传算法和模式搜索方法相结合的混合优化求解方案。文献［10］在演化加速度再入制导方法的基础上，提出了一种倾侧角剖面的线性插值模型，通过求解最大航程轨迹快速估算再入可达区。文献［11］基于Radau伪谱法对滑翔轨迹进行优化，系统地分析了升阻比、终端速度以及终端倾角对高超声速飞行器再入可达区的影响。

现有研究通常将再入可达区问题归结为复杂的轨迹优化问题，基于传统的参数搜索方法进行求解。然而，无论是采用直接法（如非线性规划理论）还是采用间接法（如极大值原理），往往需要根据工程经验，对参数初值进行预估，导致算法设计比较复杂，且鲁棒性不强。本文提出方法的创新点如下:1）以单次反转的形式对倾侧角剖面进行参数化设计，利用约束粒子群优化（PSO）算法求解了满足最大横程的再入滑翔轨迹，对于终端约束，将其作为罚函数项附加在适应度函数中，对于过程约束，则采用适应度函数极值化的方法进行处理，有效地减少了待优化变量的搜寻空间；2）传统的再入可达区计算往往需要求解多个轨迹优化问题以确定再入可达区的内外边界，而本文提出一种改进的倾侧角反转机制，仅利用一条标称再入轨迹（最大航程轨迹或常规约束轨迹），通过正向和逆向反转求解临界速度不同的倾侧角指令集合，进而得出两组机动能力不同的再入轨迹集合，即为近似的再入可达区。

1 问题描述

1.1 再入运动学方程

考虑地球自转的影响，建立如下高超声速再入滑翔飞行器的3自由度无量纲运动方程［12-13］:

式中:r为无量纲的地心距；V为再入飞行器相对地球无量纲速度；θ和φ分别为经度和纬度；γ和ψ分别为飞行航迹角和航向角；Ω为地球的自转角速度；σ为飞行器倾侧角；L和D分别为无量纲的升力加速度和阻力加速度，具体的计算公式为

式中:K=0.5R0Sref/m，R0为地球半径，Sref为飞行器的参考面积，m为飞行器质量；CL和CD分别为升力系数和阻力系数；ρ为大气密度。

1.2 再入过程约束

高超声速飞行器的再入滑翔过程必须考虑的约束影响包括热流密度约束Q、动压约束q和过载约束n，具体的计算公式［13］如下:

式中:KQ为与飞行器相关的常值参数；g0为海平面的地球引力加速度；Qmax、qmax和nmax分别为热流密度、动压和过载的最大幅值，该约束限制由高超声速飞行器自身的材料和结构所决定。（3）式～（5）式是飞行器再入滑翔过程中必须满足的硬约束条件。

1.3 再入末端约束

再入末端约束是指滑翔飞行段与末端区域能量管理段交班的约束条件，主要包括末端高度约束和末端速度约束，表达形式如下:

式中:rf和Vf分别为给定末端高度和末端速度。

1.4 再入可达区问题

现有研究主要采用再入可达区的外边界来表征再入滑翔飞行器的机动能力，包括两种典型的轮廓外形，即扇形边界和四边形边界。如图1所示，E1和E2是再入点。左侧的扇形可达区域中，E1C1表示再入飞行的最大纵程，外边界A1C1和B1C1由满足再入末端约束的点集构成。在右侧的四边形可达区域中，内边界A2B2表示再入飞行的最小纵程，外边界C2D2则由再入飞行的最大纵程所决定。本文采用扇形边界来描述飞行器的再入可达区。

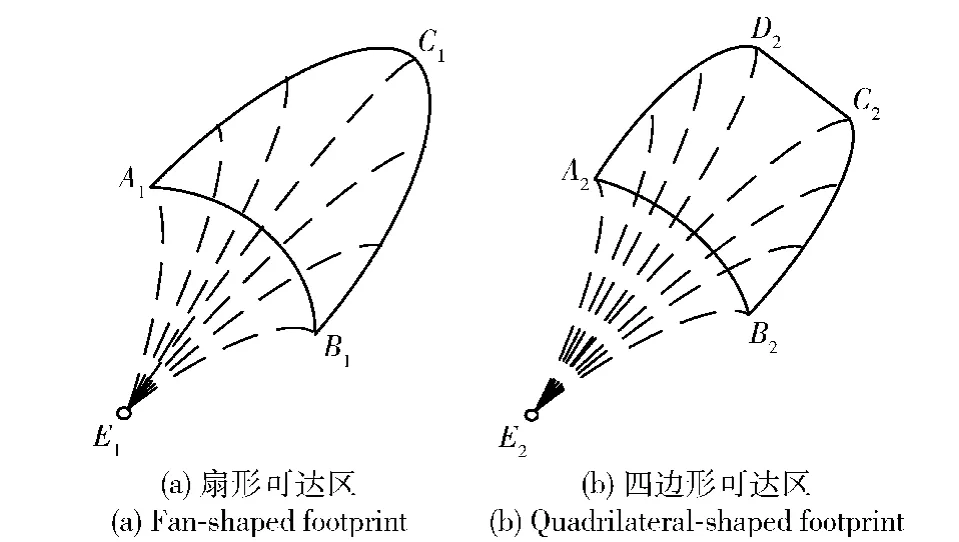
图1 再入可达区典型轮廓Fig.1 Typical shapes of landing footprints

2 再入可达区计算

2.1 概述

为了最大程度地减小待优化变量的搜寻空间以提升计算效率，本文选取标称攻角剖面和参数化的倾侧角剖面作为轨迹控制指令。首先，利用约束PSO算法求解最优滑翔轨迹。其次，通过合理设计倾侧角反转逻辑，快速生成满足约束条件的再入可达区。混合优化算法流程如图2所示。

2.2 约束PSO算法

定义｛x1，x2，…，xn｝为待优化的n个未知参数，约束范围如下:

图2 混合优化方案Fig.2 Flowchart of hybrid optimization scheme

式中:ai和bi为给定常值。

假设种群大小为N，则每个粒子k的位置x（k）和速度v（k）表示如下:

式中:x（k）和v（k）表征未知参数的搜寻空间，并不包含物理意义。根据（7）式可知，每个粒子的位置和速度的约束范围如下:

PSO算法中每个粒子代表优化问题的一个可行解，且对应一个特定的适应度函数值。通过位置更新和速度更新，整个种群的粒子不断搜索各自的最优位置。在每个周期内，通过计算粒子k的适应度函数J，可以得到该粒子当前时刻自身的最优位置pbest（k），进而求解整个粒子群当前时刻的最优位置gbest（k）.若迭代周期超过给定次数则算法终止。此时，粒子群中使适应度函数取得极值的粒子k即为问题的最优解。

每个粒子进行自身认知和群体交流主要依靠位置和速度更新，计算公式［14-15］如下:

式中:c1和c2为学习因子；r1和r2是服从U（0，1）分布的随机数；w是惯性权重，计算公式为

式中:wmax和wmin为最大和最小惯性系数；Nmax为最大迭代周期；Nx为当前迭代周期。

轨迹优化问题包含复杂的终端约束和过程约束，因此，有效地处理等式和不等式约束尤为关键。本文对传统的PSO算法做出改进，对于等式约束，将其进行变换后，作为罚函数项加入到适应度函数中，具体的表达形式如下:

式中:ζp≥0（p=1，2，…，m）为罚函数因子；dp（x）代表与未知参数相关的m个等式约束。

对于不等式约束，本文采用适应度函数极值化的处理方法，即粒子k在更新自身位置或速度时，若不满足任何一个不等式约束，则将该粒子当前时刻对应的适应度函数极值化，即J′（k）=∞，同时将该粒子的速度置0，即v（k）=0.通过对不满足不等式约束的粒子进行适应度函数极值化，可以有效地处理再入轨迹优化问题中存在的硬约束条件。

2.3 轨迹优化设计

考虑到再入飞行器初始下降段的热保护要求，本文采用升力式再入滑翔飞行中典型的二次分段标称攻角剖面，表达形式［16］如下:

式中:α0为再入攻角初值；Vα为飞行器攻角变化的临界速度；K为常值参数。

为了减小约束PSO算法中未知变量的搜索空间，本文选取参数化的倾侧角剖面作为轨迹控制指令，其表达形式如下:

式中:σ0和σ1分别为倾侧角剖面的初值和终值；V1和V2为临界速度。在初始下降阶段，气动特性较弱，故选取常值倾侧角指令σ0作为控制指令。接近末端区域能量管理阶段时，为了保证飞行器的平稳飞行，选取常值倾侧角指令σ1作为控制变量。初始下降段（临界速度为V2）与末端能量管理段（临界速度为V1）之间区域的倾侧角指令则按照线性规律进行递增或递减。

根据再入初始航向角与目标位置的关系，重新定义倾侧角剖面的表达形式。如图3所示，定义Δψ为再入航向角ψ0与目标视线角ψT的差值，则倾侧角剖面的线性递增或递减曲线可以表示为如下形式:

式中:参数K0和K1可由σ0和σ1变换得到，考虑到再入初始航向与目标视线角之间的位置关系，按照如下规则确定参数化倾侧角剖面（16）式、（17）式中的未知参数［12］:

1）若Δψ=ψ0-ψT＞0，则取σ1＞σ0，σ1＞0，即K1＜0，σ1＞0；

2）若Δψ=ψ0-ψT＜0，则取σ1＜σ0，σ1＜0，即K1＞0，σ1＜0.

图3 参数化倾侧角剖面Fig.3 Parameterized bank angle profile

通过将倾侧角剖面进行参数化设计，约束PSO算法中的未知参数仅有4个，即（σ0，σ1，V1，V2）或（K0，K1，V1，V2），有效地提高了轨迹优化速度。为了得到具有最大横程的滑翔轨迹，选取如下适应度函数:

式中:Rcro为再入滑翔飞行的横向航程，近似计算公式为

式中:θt和φt分别是再入滑翔段和末端能量管理段交接时刻的经度和纬度。

改进的PSO算法能够有效地处理再入过程约束和再入末端约束。具体方法如下:每个进化周期内，若任何一个粒子k在更新自身位置和速度时，使得热流密度约束（3）式、动压约束（4）式或过载约束（5）式超出了给定限度，则将该粒子当前时刻对应的适应度函数极值化，并将该粒子的速度置0.这样，可以有效地保证再入轨迹满足以上硬约束条件。对于末端高度约束和末端速度约束，本文将其作为罚函数项附加于适应度函数，具体的表达式如下:

则利用改进的约束PSO算法，能够求解具有最大横程的再入滑翔轨迹。由于篇幅所限，本文对再入滑翔轨迹的平滑性没有进行约束，相关技术细节可参考文献［17］.

2.4 倾侧角反转逻辑

本文设计一种倾侧角正向和逆向反转逻辑，以实现再入滑翔飞行器可达区域的快速估算，基本原理如下:

1）倾侧角正向反转是指当再入飞行速度低于某一临界速度时，对倾侧角指令进行反转，其幅值保持不变。如图4所示，记最大横程轨迹对应的倾侧角剖面为σcmd，给定临界速度为V+，则倾侧角正向反转逻辑的表达形式如下:

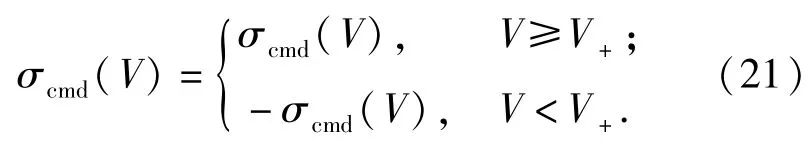
2）倾侧角逆向反转是指当再入飞行速度高于某一临界速度时，对倾侧角指令进行反转，其幅值保持不变。若给定临界速度为V-，则倾侧角逆向反转逻辑的表达形式如下:

再入可达区的近似计算方法为:将最大横程轨迹对应的参数化倾侧角剖面分别进行正向和逆向反转处理，能够快速得到不同临界速度下的反转倾侧角指令集合。倾侧角反转机制仅仅改变控制指令的符号，而不改变其幅值，故反转倾侧角指令集合中的所有控制剖面不会对再入飞行器的纵向制导产生影响，进而保证了再入末端高度和末端速度满足能量管理段的约束要求。利用反转倾侧角指令集合中的控制剖面对运动学方程进行递推解算，可以得到具有不同机动能力的再入轨迹集合，该集合即为再入滑翔飞行器的近似可达区域。本文提出的倾侧角反转逻辑以一条标称再入轨迹（最大航程轨迹或常规约束轨迹）为基准，能够直接生成两组满足约束的轨迹集合，为中途进行任务重规划的飞行器提供变更或选择潜在目标的参考可达区域，体现了本文的求解方案在应对突发事件时具有快速性优势。

图4 倾侧角正向/逆向反转逻辑Fig.4 Forward/backward bank angle reversal logic

3 仿真分析

本文以升力式高超声速再入飞行器CAV-H为对象进行仿真验证，主要特征参数为［18］:飞行器质量m=907.2 kg，气动面积Sref=0.483 9 m2，热流密度约束Qmax=0.6 MW/m2，动压约束qmax=60 kPa，过载约束nmax=2.5 g.

飞行器的初始再入状态如表1所示。末端高度约束和速度约束为hf=23 km，Vf=1 500 m/s.标称攻角剖面参数为K=0.21，α0=30°，VT的Ma数为14.倾侧角指令范围为-60°～60°.

表1 飞行器初始再入状态Tab.1 Initial reentry conditions of the vehicle

约束PSO算法参数为:wmax=0.9，wmin=0.4，c1=c2=1.496 2，Nmax=60，N=30.仿真计算机是Windows XP操作系统，主频3.0 GHz，内存2.0 GB.程序采用标准C/C++语言编写。

图5和图6给出了利用约束PSO算法求解最大横程轨迹的仿真结果，并得出了以下结论:

1）由结果可知，仿真飞行时间约20 min，末端飞行高度和末端飞行速度均满足再入滑翔段和末端区域能量管理段的交班条件要求，验证了引入罚函数处理再入末端约束的可行性。

2）如图5所示，再入滑翔轨迹严格满足热流密度、动压和过载等硬约束条件，说明将适应度函数进行极值化，可以有效处理再入过程约束。

3）如图6所示，改进的PSO算法递推17次后收敛，虽然得到的最大横程轨迹并非全局最优（因为倾侧角剖面进行了参数化设计），但未知参数的减少极大程度上缩小了搜寻空间，使得轨迹优化时间不到4 s，验证了算法的时效性。

图7～图10给出了利用倾侧角正向反转和逆向反转进行再入可达区近似计算的仿真结果，并得出了以下结论:

图5 轨迹优化仿真结果Fig.5 Simulated results of optimal trajectory

图6 适应度函数曲线Fig.6 Result of fitness function

图7 倾侧角逆转采样结果Fig.7 Examples of bank angle profile reversal

1）如图7所示，虽然倾侧角正向和逆向反转所选取的时刻与方向各不相同，但其仅仅改变了控制指令的符号，不改变其幅值，故不会对再入纵向制导产生影响，进而满足了再入末端高度约束和末端速度约束。

2）如图8所示，利用倾侧角正向和逆向反转机制，可以在一条标称再入轨迹的基础上分别生成两组满足终端约束和过程约束的再入轨迹集合，将轮廓相似的两个目标覆盖区域叠加，即可得到近似的再入可达区。

图8 再入可达区仿真结果Fig.8 Simulated result of landing footprint

3）图9给出了倾侧角反转指令集合，该集合由最大横程轨迹的倾侧角剖面直接生成，其反转时刻和反转方向的设计灵活，有利于算法程序的实现，体现了一定的工程应用前景。

图9 倾侧角逆转指令集合Fig.9 Set of bank angle commands

4）图10给出了本文方法与传统伪谱法［11，19］的仿真结果对比。从中可以看出，本文的结果与Gauss伪谱法得出的可达区形状基本一致，由于本文对倾侧角剖面进行了参数化设计，因此计算可达区面积略小于伪谱法的优化结果，然而本文方法仅需求解一条最优轨迹，大大缩短了计算时间，故可用于突发事件下可达区域的快速估算。

4 结论

本文针对升力式高超声速飞行器再入可达区问题，提出了约束粒子群优化和倾侧角反转相结合的混合求解方案，研究分析和仿真结果表明:

1）改进的PSO算法易于实现，且无需根据工程经验预估参数初值，增强了轨迹优化算法的可操作性。

图10 仿真结果对比Fig.10 Comparative results

2）采用参数化倾侧角剖面设计，极大程度上缩小了未知变量的搜寻空间，提升了再入轨迹优化算法的时效性。

3）利用倾侧角正向和逆向反转逻辑直接生成控制指令集合，进而快速得到高超声速飞行器的再入可达区，与传统Gauss伪谱法相比，采用本文方法所求解的可达区结果虽然偏于保守，但可以缩短计算时间，在突发事件下可达区的快速估算方面具有应用前景。

（

）

［1］ Zhao J，Zhou R，Jin X.Progress in reentry trajectory planning for hypersonic vehicle［J］.Journal of Systems Engineering and Electronics，2014，25（4）:627-639.

［2］ Sarah N D，Nesrin S K.Survey of planetary entry guidance algorithms［J］.Progress in Aerospace Sciences，2014，68（1）:22-28.

［3］ 袁宴波，张科，薛晓东.基于Radau伪谱法的制导炸弹最优滑翔弹道研究［J］.兵工学报，2014，35（8）:1179-1186. YUAN Yan-bo，ZHANG Ke，XUE Xiao-dong.Optimization of glide trajectory of guided bombs using a Radau pseudo-spectral method［J］.Acta Armamentarii，2014，35（8）:1179-1186.（in Chinese）

［4］ Zhao J，Zhou R，Jin X.Gauss pseudospectral method applied to multi-objective spacecraft trajectory optimization［J］.Journal of Computational and Theoretical Nanoscience，2014，11（10）: 2242-2246.

［5］ 张冉，李惠峰.基于平衡滑翔的升力再入攻角设计分析及应用［J］.宇航学报，2012，33（11）:1557-1563.ZHANG Ran，LI Hui-feng.Angle of attack operation zone analysis and application based on equilibrium glide condition for lifting reentry［J］.Journal of Astronautics，2012，33（11）:1557-1563.（in Chinese）

［6］ Lu P，Xue S.Rapid generation of accurate entry landing footprints［J］.Journal of Guidance Control and Dynamics，2010，33（3）: 756-767.

［7］ Li H F，Zhang R.Footprint problem with angle of attack optimization for high lifting reentry vehicle［J］.Chinese Journal of Aeronautics，2012，25（2）:243-251.

［8］ 傅瑜，杨卫丽，崔乃刚.升力式再入飞行器覆盖范围计算分析［J］.哈尔滨工业大学学报，2012，44（11）:13-19. FU Yu，YANG Wei-li，CUI Nai-gang.Calculation of reachable landing locations of lift entry vehicle［J］.Journal of Harbin Institute of Technology，2012，44（11）:13-19.（in Chinese）

［9］ 李惠峰，孙国庆，何睿智.基于混合优化算法的RLV覆盖区求解［J］.中国空间科学技术，2012，32（6）:39-46. LI Hui-feng，SUN Guo-qing，HE Rui-zhi.Footprint optimization for RLV based on mix optimal algorithm［J］.Chinese Space Science and Technology，2012，32（6）:39-46.（in Chinese）

［10］ Leavitt J A，Mease K D.Feasible trajectory generation for atmospheric entry guidance［J］.Journal of Guidance Control and Dynamics，2007，30（2）:473-481.

［11］ 李柯，聂万胜，冯必鸣.助推滑翔飞行器可达区域影响因素研究［J］.现代防御技术，2013，41（3）:42-47. LI Ke，NIE Wan-sheng，FENG Bi-ming.Affecting factor of footprint for boost-glide vehicle［J］.Modern Defence Technology，2013，41（3）:42-47.（in Chinese）

［12］ Zhao J，Zhou R.Particle swarm optimization applied to hypersonic reentry trajectories［J］.Chinese Journal of Aeronautics，2015，28（3）:822-831.

［13］ Zhao J，Zhou R.Reentry trajectory optimization for hypersonic vehicle satisfying complex constraints［J］.Chinese Journal of Aeronautics，2013，26（6）:1544-1553.

［14］ Maurice C，James K.The particle swarm-explosion，stability，and convergence in a multidimensional complex space［J］.IEEE Transactions on Evolutionary Computation，2002，6（1）:58-73.

［15］ Gerhard V，Jaroslaw S.Particle swarm optimization［J］.AIAA Journal，2003，41（8）:1583-1589.

［16］ 赵江，周锐.考虑禁飞区规避的预测校正再入制导方法［J］.北京航空航天大学学报，2015，41（5）:864-870. ZHAO Jiang，ZHOU Rui.Predictor-corrector reentry guidance with no-fly zone constraints［J］.Journal of Beijing University of Aeronautics and Astronautics，2015，41（5）:864-870.（in Chinese）

［17］ 赵江，周锐.基于倾侧角反馈控制的预测校正再入制导方法［J］.兵工学报，2015，36（5）:823～830. ZHAO Jiang，ZHOU Rui.Predictor-corrector reentry guidance based on feedback bank angle control［J］.Acta Armamentarii，2015，36（5）:823-830.（in Chinese）

［18］ Zhao J，Zhou R，Jin X.Reentry trajectory optimization based on a multistage pseudospectral method［J］.Scientific World Journal，2014，878193:1-13.

［19］ 汪雷，刘欣，杨涛，等.高超声速滑翔式飞行器目标覆盖范围的计算方法［J］.弹道学报，2014，26（1）:50-55. WANG Lei，LIU Xin，YANG Tao，et al.Footprint calculation for hypersonic glide vehicle［J］.Journal of Ballistics，2014，26（1）:50-55.（in Chinese）

Landing Footprint Computation Based on Particle Swarm Optimization

ZHAO Jiang，ZHOU Rui
（School of Automation Science and Electrical Engineering，Beihang University，Beijing 100191，China）

To enforce the flexibility of the landing footprint computation，a hybrid optimization method based on the constrained particle swarm optimization（PSO）and bank angle reversal logic is proposed for the lifting hypersonic reentry vehicles.The parameterized bank angle profile is developed in order to reduce the searching space of the unknown variables.An improved PSO algorithmis used to optimize the reentry gliding trajectory satisfying both the path and the terminal constraints.The set of bank angle commands is obtained by imposing the forward and backward bank angle reversal logics，which can fast generate the approximate landing footprint for hypersonic reentry vehicles.Based on the high-lifting common aerial vehicle（CAV-H）model，a numerical simulation is performed.The results show that the hybrid optimization method is simple in design and independent of the initial estimation of the unknown parameters.The results also demonstrate the feasibility of the proposed algorithm for rapid generation of the landing footprint.

ordnance science and technology；particle swarm optimization；landing footprint；hypersonic vehicle；bank angle reversal logic

V448.235

A

1000-1093（2015）09-1680-08

10.3969/j.issn.1000-1093.2015.09.012

2014-12-29

国家自然科学基金项目（61273349、61203223）

赵江（1986—），男，博士研究生。E-mail:jzhao@buaa.edu.cn；周锐（1968—），男，教授，博士生导师。E-mail:zhr@buaa.edu.cn