混合梁斜拉桥现浇梁端索道管定位精度控制★

陈 康 黄天贵 李政逊

(中交第一公路工程局有限公司，北京 100024)

0 引言

大型斜拉桥主要由塔、梁、索三大部分组成。斜拉索是连接主塔和主梁的纽带，而索道管是将斜拉索两端分别锚固在主塔和主梁上的重要构件，为了防止斜拉索与索道管口发生摩擦而损坏斜拉索，影响工程质量，以及保证对称，防止锚固定偏心而产生的附加弯矩超过设计允许值，对索道管锚垫板中心和现浇梁顶面索道管出口中心的三维空间坐标位置提出了很高的精度要求，按大型斜拉桥设计规定，一般要求斜拉索、锚具轴线偏差小于±5 mm［1］。斜拉索通常采用扇形布置，现浇梁端的索道管分布在边跨位置，它们分布相对密集，倾角变化大，索道管长度变化大。

本文以永川长江大桥现浇端索道管安装为背景，在现浇端索道管精确定位控制方面进行简单的探讨。

1 工程概况

永川长江大桥桥型为七跨连续半漂浮体系双塔双索面混合梁斜拉桥，跨型布置为(64+2×68+608+2 ×68 +64)m;主梁中跨采用PK 断面钢箱梁，边跨采用同外形的混凝土箱梁，梁高3.5 m，箱梁全宽(含风嘴)37.6 m;中跨标准索距15.5 m，边跨索距10 m，8 m(见图1)。

图1 斜拉索总体布置图

在斜拉桥边跨混凝土梁的施工中，索道管的精密定位十分重要，受实际施工条件限制，现浇梁端索道管的定位施工放样困难，但精度要求高。永川长江大桥，定位精度要求平面位置偏差小于±5 mm，高程偏差小于±2 mm［2］。大桥边跨现浇梁南北岸各长196 m，分别布设19 对索道管，其中倾角最大为80.114°，最小为37.818°，索道管最长为5.293 m，最短为3.310 m。一般情况，索道管越长，体积越大，重量越重，则相对应的定位难度越大。在索道管安装前，放样锚固点中心点位置，提前安装型钢支架，作为初步定位用，以备后期安装微调使用。

2 大桥坐标系统和测量仪器

大桥建立了大桥独立坐标系和投影面，测量仪器使用现代先进仪器。

2.1 大桥独立坐标系和投影面

为了方便设计和施工，以桥轴线右岸端点坐标为起算坐标，桥轴线方位为起算方位角。设计桥面高程面是主要投影面，因桥梁上部结构安装，能否尽量减小变形，关键在此投影面的确定，设计成果的投影面为250 m。

2.2 测量仪器

测量仪器使用徕卡TCRP1201 +R400 全站仪，标称测角精度0.5″，测距在有棱镜模式时的测距精度为1 mm +1.5 ×10－6D，无棱镜模式时的测距精度为2 mm+2 ×10－6D。

3 索道管设计坐标的计算与修正

3.1 索道管设计坐标利用数学模型计算

不考虑边跨现浇梁动态施工特性时的索道管三维坐标旋转模型。现以永川长江大桥南岸边跨现浇梁索道管为例，推导不考虑现浇梁动态施工的特性，即设计成桥状态时的索道管测量放样数据计算的数学模型。

图2 索道管数学模型图

如图2 所示，假设AD 为索道管中心线，A 为索道管下端锚固点，D 为索道管出口点，AB 为索道管中心线在Y 轴面上的投影，AE 为索道管中心线在X 轴面上的投影，BDEC 为索道管出口中心点所在的水平面，L 为索道管设计长度，m 为索道管中心线在BDEC 面的投影，h 为索道管锚固中心点到索道管出口中心点高差，β 为索道管的竖直角，γ 为索道管的水平角，高程已知z锚，索道管锚固点中心点平面坐标已知为(x锚，y锚)，以此建立立体模型，计算如下:

把式(2)代入式(1)可计算出:

把式(3)，式(4)代入式(2)，再将结果代入式(1)可以推算出:

因为，L，β 角，γ 角都为已知量，所以可以计算出h。得出h后，将h 代入式(3)，式(4)可算出Δx 和Δy。

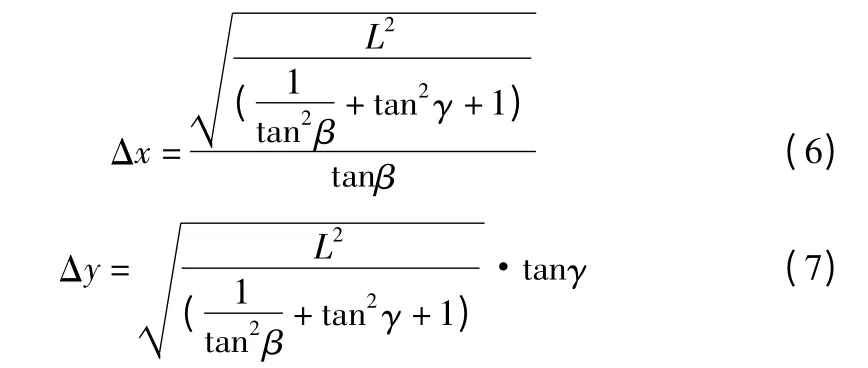
其中，h，Δx 和Δy 三个量全部求出，又已知锚固点三维坐标，可算出索道管出口坐标:

3.2 数据修正

在现浇梁索道管精密定位过程中，由于在钢管支架上立模、钢筋绑扎等施工荷载的增加，往往使现浇梁底模发生沉降，而偏离设计。所以，在索道管的实际定位过程中应充分考虑上述因素并对索道管的实际放样数据做出修正。索道管设计参数的修正应主要考虑桥梁顺桥向(x)、横桥向(y)及坐标高程(z)偏差这三个因素。这三个因素是通过高程和倾斜角的修正来同时完成的，而且要结合现场时间情况进行修正的完善，只理论上进行修正而不与实际情况相结合所定位的索道管是不正确的。永川长江大桥是混合梁斜拉桥，对成桥状态下索道管测量放样数据计算模型进行修正时，应在斜拉索区施工前期，对现浇梁进行24 h 的变形观测，根据变形观测数据与原有的数学计算模型进行对比和修正。但考虑永川长江大桥边跨现浇梁跨径比较大，分三个梁段进行浇筑，所以每完成一个浇筑工况，应重新对现浇端进行24 h 的变形观测，再与数学模型计算的数据进行对比与修正，从而使索道管放样数据计算的方法更趋向科学合理。

1)索道管倾斜角的修正。

由于钢筋绑扎、浇筑过程中锚垫板位置在下方且重量较大，变形量较大，从而导致索道管的倾斜角发生变化。下面就倾斜角的修正做简要分析。如图3 所示，AB 为水平面，AC 为索道管锚块设计坡度线，AC1为索道管锚块实际坡度线，C(C1)为索道管锚固点，β 为索道管倾角，α 为设计坡度，θ 为索道管中心线与设计坡度线的夹角。

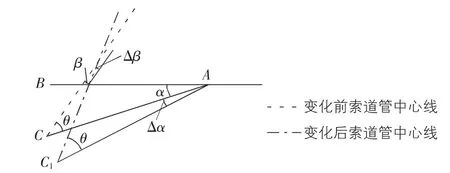
图3 索道管施工前后变化

永川长江大桥索道管现浇梁端，AC 为负坡，α 为负，由图3 可知:

当坡度变化了Δα 时(取向下为正)，C 位置移动到C1，为保证索道管中心线与设计坡度线的夹角θ 不变，α 也必须作相应的改正。结合上文叙述的公式不难看出:

根据上述原理，在索道管定位之前，应先把索道管实际的坡度与设计的坡度之差Δα 和锚固中心点实际与设计高差ΔH，计算测量得出，从而计算出改正后的倾角，即:

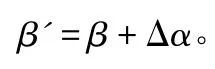
2)现浇梁底模标高定位偏差引起的锚固点高程修正。

假定沉降定位偏差引起的高程偏差为ΔH，为保证斜拉索的线性，现浇梁端索道管的标高也应该改变相同的偏差量，由于索道管上其他坐标的计算都是从锚固点起算的，因此只需对锚固点进行此项修正即可。修正后锚固点的高程为:

4 结语

大型混合梁斜拉桥工程的建设需要测量数据更加精准，对精度的要求更高。理论值必不可少，但还需在理论的基础上结合现场的实际进度、施工条件等对理论值做修正处理，以更加完善的数据进行测量，这样可以保证桥梁整体的精准度。

本文从坐标计算和修正两方面对混合梁斜拉桥现浇端索道管定位精度做了简单的分析，但是对索道管精度定位的因素不只是有本文论述内容，还有其他，如:大气温度、斜拉索垂曲等，都需要根据当时施工的实际条件来适当修正，以保证索道管定位的精度，保证工程质量。

［1］吴栋材，谢建纲.大型斜拉桥施工测量［M］.北京:测绘出版社，1996.

［2］JTG/T F50—2011，公路桥涵施工技术规范［S］.