屈曲约束支撑在教学楼设计中的应用研究★

石 勇 尚世力 卢晓明 岳焱超 王新娣

(1.太原理工大学建筑设计研究院，山西 太原 030024;2.西安交通大学，陕西 西安 710049;3.上海蓝科建筑减震科技股份有限公司，上海 200082)

0 引言

自2008 年汶川地震以后，国家进一步加大了对防灾抗震领域的投入。随后修订的GB 50011—2010 建筑抗震设计规范［1］扩大了隔震和消能减震房屋的适用范围，并对消能技术做了重点介绍。甘肃省，山西省有关部门也相继出台了关于在学校医院等乙类建筑中强制性采用减隔震技术的文件。传统经验表明［2］:单一抗侧力结构体系相比于双重抗侧力结构体系更易于倒塌，且破坏程度更大。纯框架结构就属于一种单一抗侧力体系结构，但是若采用屈曲约束支撑后就会使结构成为双重抗侧力体系，地震发生时，混凝土框架和屈曲约束可以同时为结构抗震的两道防线，其中屈曲约束支撑作为结构抗震的第一道防线，作用类似于电器元件中保险丝，在地震发生时先于框架梁柱破坏，从而使整体结构具有更加优良的抗震性能以及抗侧能力，使得结构更加安全。

屈曲约束支撑在受拉以及受压时均可屈服，延性较好，滞回曲线更为饱满，不仅可以作为抗侧力构件提高结构的侧向刚度，同时又作为消能支撑，在屈服耗能的过程中实现消能减震［3，4］。国际上，将屈曲约束支撑运用于抗震工程实际的做法很多［5，6］，但一般都是用于钢结构建筑中，而将其作为混凝土结构抗侧力构件的应用还在不断的研究中。本文结合某中学教学楼的实例，具体阐述了屈曲约束支撑对框架结构抗震性能的提升作用。

按照抗震设计规范［1］规定要保证结构小震不坏，即在小震时结构处于弹性阶段，弹性阶段设计采用的是PKPM 中SATWE 模型进行弹性设计，可以满足抗震规范［1］对结构小震不坏的要求。只考虑结构在小震不坏是不够的，抗震规范还要求结构在罕遇地震下不倒，以保证在发生大震时人民生命财产安全，大震不倒，需要对结构做弹塑性分析，目前弹塑性分析的软件有很多，本文采用MIDAS GEN 对结构进行弹塑性分析，来验算结构是否满足大震不倒的要求。

1 工程概况

在建的中学位于某8 度区，占地面积1 284 m2，总建筑面积15 020 m2，包括教学楼，行政楼，实验楼等，其中教学楼面积为3 793 m2，该建筑地上5 层，局部6 层，室内外高差0.3 m～1.2 m。本文主要介绍教学楼的屈曲约束支撑的应用情况。

本工程采用框架—支撑结构体系，屈曲约束支撑采用同济大学研制，上海蓝科减震公司经销的屈曲约束支撑，其整体结构模型见图1a)，平面布置图见图1b)。

2 结构设计

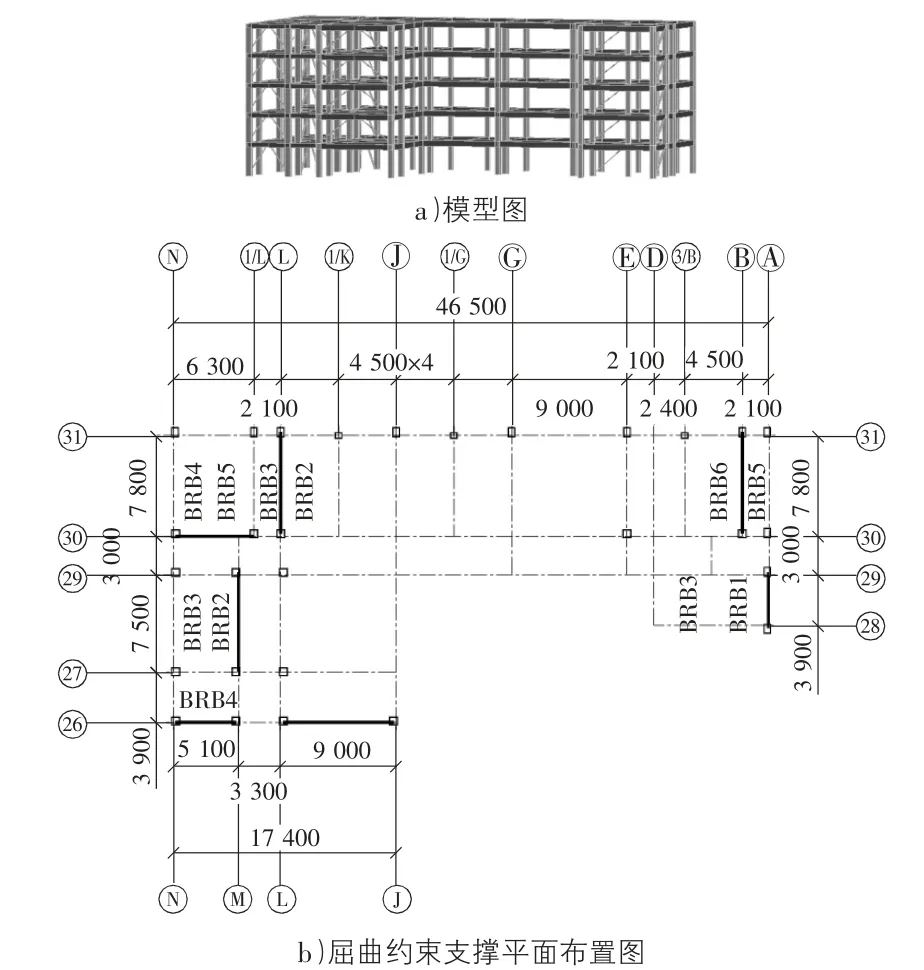
图1 工程结构模型及BRB 平面布置图

结构设计的基本参数和主要构件截面如表1 所示。

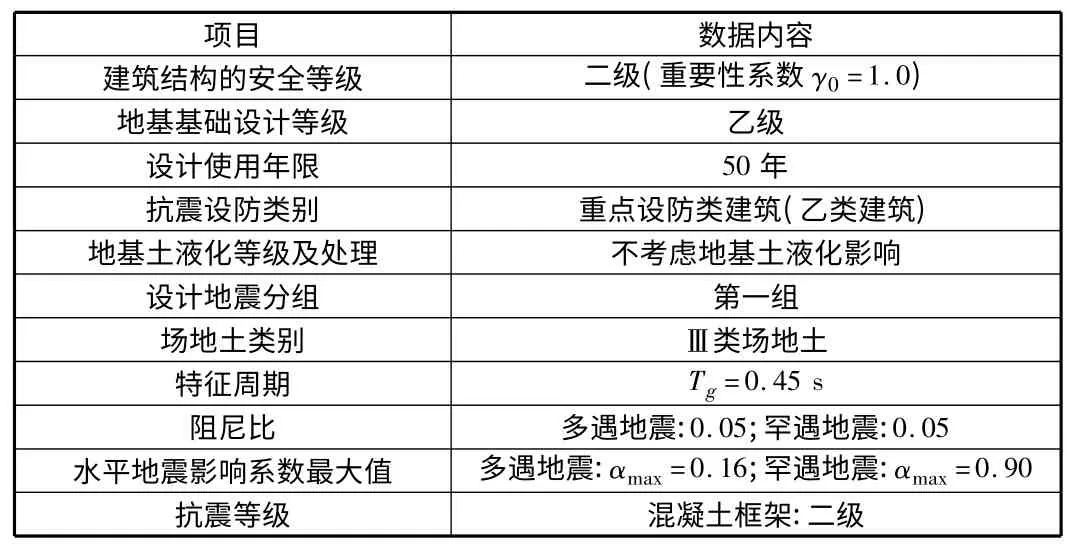
表1 设计基本参数

本项目如果只采用纯框架结构，结构的抗侧刚度将无法满足要求，并且也无法满足规范中层间位移角的要求［7］，此时若采用其他解决方式，比如加大柱截面，势必会影响建筑空间的使用，从而影响建筑的使用功能，因此这种做法是不合理的;而若是改用框剪结构，通过局部布置剪力墙来提高抗侧能力，又会影响建筑的外立面效果，从而带来新的问题;如果采用普通钢支撑，在地震作用下支撑承受轴力会很大，很容易出现屈曲，为避免支撑屈曲势必会加大支撑截面，从而使支撑在地震作用下受力更大［9］，所以这种做法同样不可取。本文采用屈曲约束支撑来设计此教学楼，不仅使结构的抗侧刚度显著提高，同时又能显著减小支撑截面和节点区的剪力，符合结构设计经济安全合理的要求。

在结构的特定位置设置一些屈曲约束支撑，可以使结构的层间位移、扭转位移比、平扭周期比等整体指标满足规范要求。屈曲约束支撑的设计需要根据结构所需抗侧刚度来确定芯板截面。屈曲约束支撑的承载力是通过受力分析计算得到的。屈曲约束支撑型号见表2。

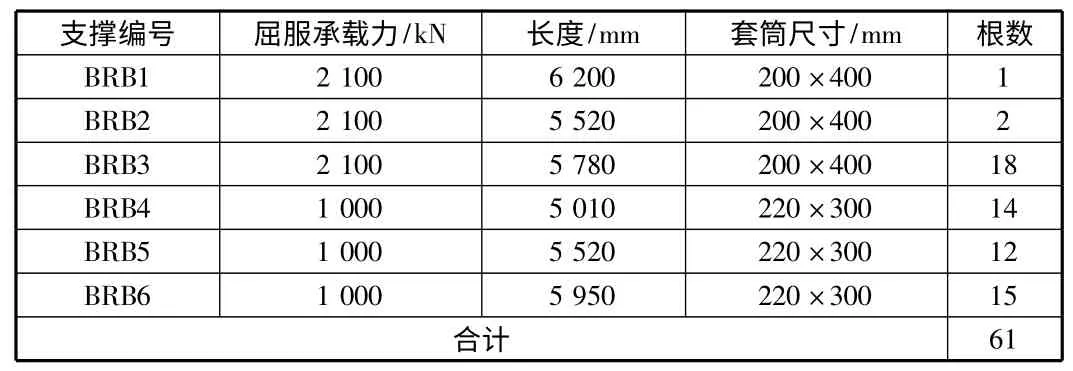
表2 屈曲约束支撑型号表

3 多遇地震作用下的结构分析计算

首先在弹性阶段采用的是SATWE 模块对该结构进行计算分析，并对两种计算方案进行比较:一种是没有用屈曲约束支撑的普通方案，另一种是采用屈曲约束支撑的方案，两种方案的计算结果见表3，表4。

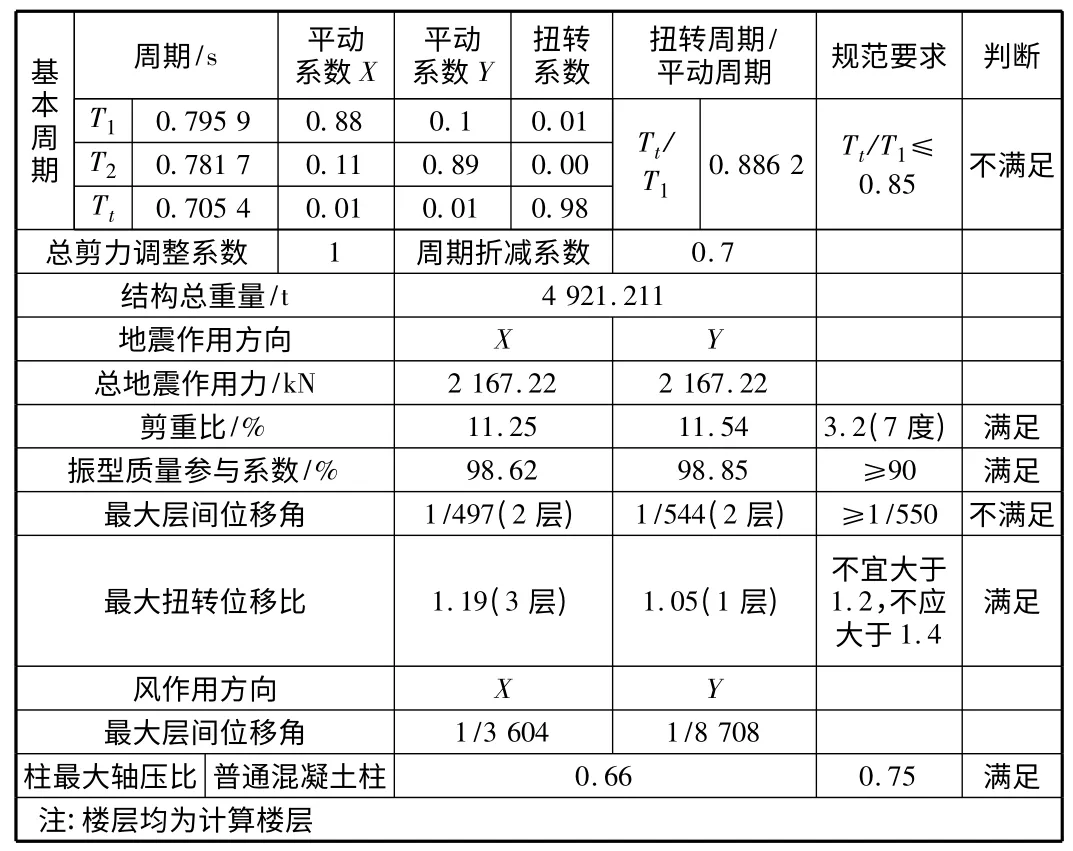
表3 无屈曲约束支撑方案计算结果

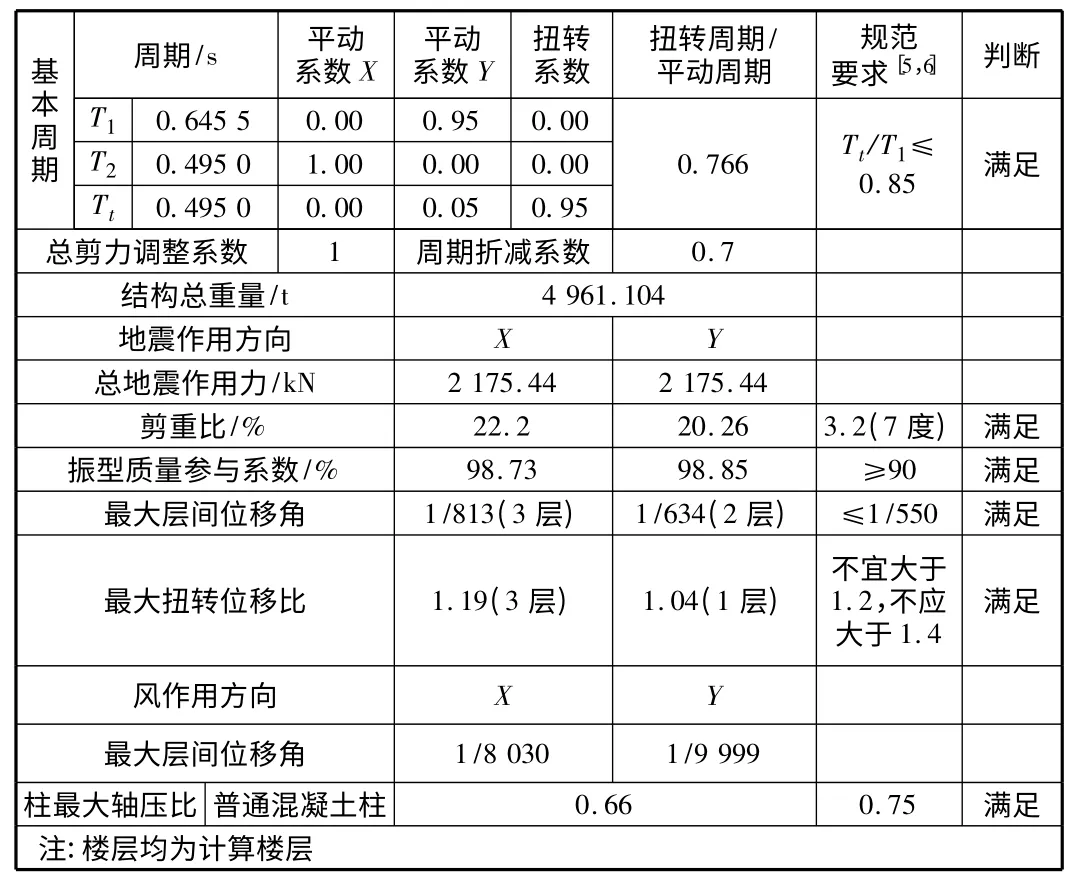
表4 屈曲约束支撑方案计算结果

通过上述计算可以得出，对于纯框架而言结构的抗侧刚度明显不足，X 向和Y 向层间位移角不符合规范;但是采用屈曲约束支撑方案就可以很好的满足规范要求。

图2 表示X 方向和Y 方向的层间位移角曲线，屈曲约束支撑大幅提高了上部结构的抗侧刚度，弱化了地震发生时结构的位移响应。

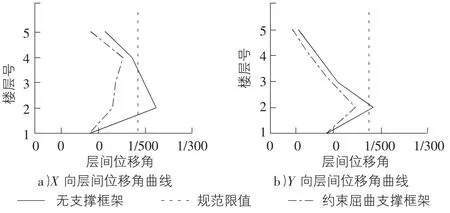
图2 层间位移角曲线

通过PKPM 中的计算可知在多遇地震下，部分楼层BRB 的应力为0.8～0.9，其余多数在0.5 左右，可以满足BRB 在小震下弹性性能要求，预计在设防地震中部分支撑开始屈服，但大部分的支撑仍处于弹性工作阶段。总体上，屈曲约束支撑使结构自重仅仅增加39.893 t，远小于结构自重(不到0.9%)，但是却使得结构的抗侧刚度得到明显改善，使得结构的抗震性能明显增强，并且屈曲约束支撑易于安装，减少了现场作业，提高了施工效率，使综合性效益实现最大化。

4 罕遇地震作用下的结构分析计算

本工程采用MIDAS GEN 对屈曲约束支撑—混凝土框架结构进行PUSHOVER 静力弹塑性分析，来验算结构是否满足抗震规范对结构大震不倒的要求。

4.1 MIDAS GEN 与PKPM 的弹性阶段对比

为了保证MIDAS GEN 分析的可靠性，将MIDAS GEN 与PKPM 的弹性设计阶段进行对比，主要对比参数见表5。

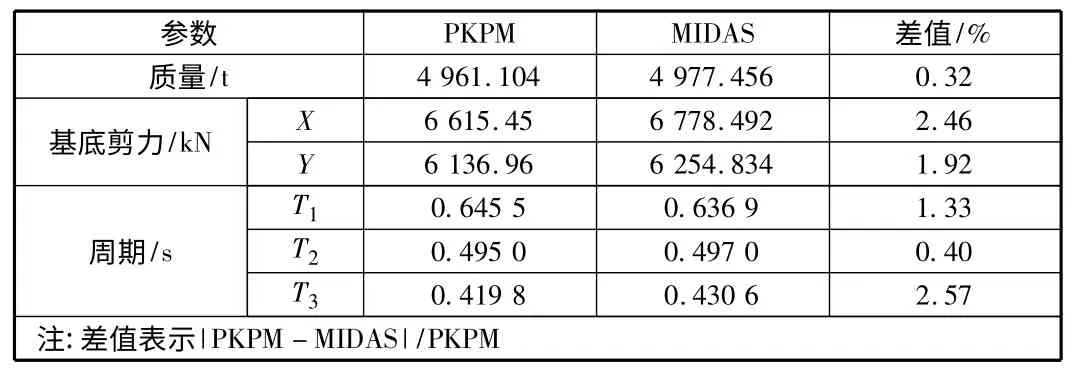
表5 PKPM 与MIDAS GEN 主要参数对照表

通过表5 分析，PKPM 与MIDAS GEN 在弹性阶段计算误差都在10%以内，两个软件计算吻合的很好，因此可以认为静力弹塑性的分析模型跟弹性分析模型是一致的。

4.2 梁、柱、支撑的塑性铰参数设置

梁端设置MIDAS 提供的缺省的自动混凝土梁弯曲My 铰本构模型，柱顶和柱底设置MIDAS 提供的缺省的钢柱自动PMM铰本构模型，屈曲约束支撑根据本身特性定义的P 铰本构模型，参数主要由屈曲约束支撑的屈服强度和刚度折减系数确定，屈服位移由计算机自动计算，屈曲约束支撑的主要参数如表6所示。

4.3 大震作用下的性能点确定

通过对模型X 和Y 方向推覆分析来寻求8 度(0.2g)地震作用下结构的性能点。将PUSHOVER 计算得到的力—位移关系和大震下的反应谱分别转换为能力谱和需求谱，并统一绘在坐标系中，见图3。

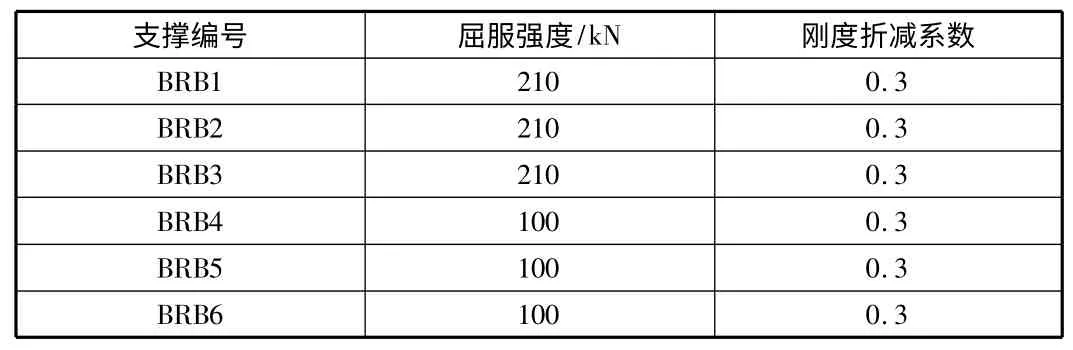
表6 屈曲约束支撑P 铰本构参数

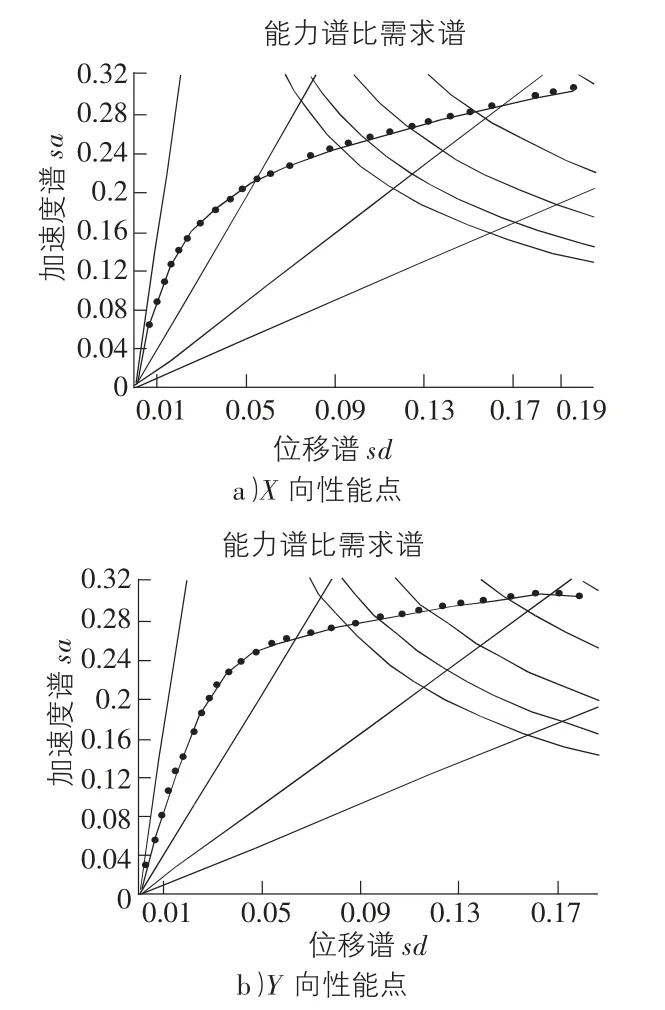
图3 PUSHOVER 分析性能点

由图3 可以得到大震性能点处的基底剪力，定点位移及阻尼比情况，具体值见表7。

表7 性能点处的主要参数值

4.4 罕遇地震下出铰情况

图4 是在罕遇地震下结构中支撑出铰情况，图5 是在罕遇地震下结构中梁出铰情况，图6 是在罕遇地震下结构中柱出铰情况。在罕遇地震下，屈曲约束支撑先于梁柱出铰，在梁柱出铰顺序中，梁先于柱出铰，结构整体设计满足“强柱弱梁”，屈曲约束支撑作为结构第一道防线，最先出铰耗能，屈曲约束支撑消耗的地震能量，使得地震对梁柱的破坏大大减轻，达到了预期设计目的。

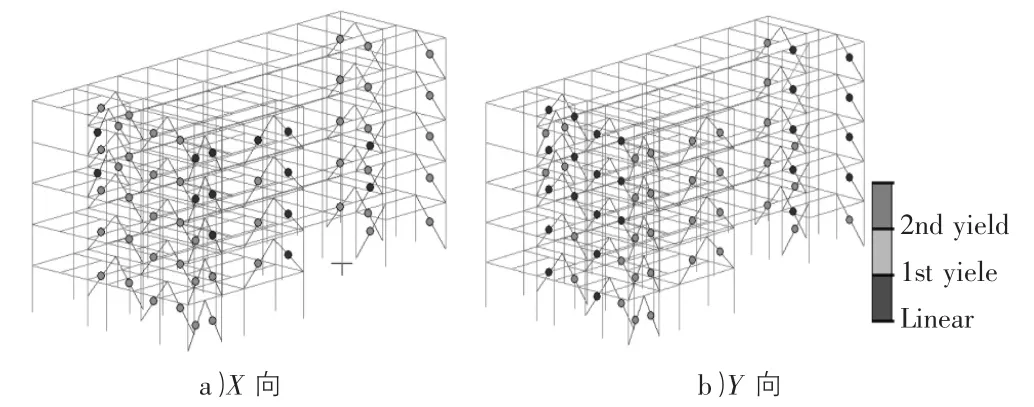
图4 屈曲约束支撑出铰示意图

4.5 罕遇地震作用下弹塑性分析的层间位移及层间位移角

图7 是在罕遇地震作用下进行弹塑性分析得到的层间位移，图8 是在罕遇地震作用下进行弹塑性分析得到的层间位移角，由图7，图8 得到的最大层间位移和最大层间位移角具体数据如表8所示。

图5 梁出铰示意图

图6 柱出铰示意图

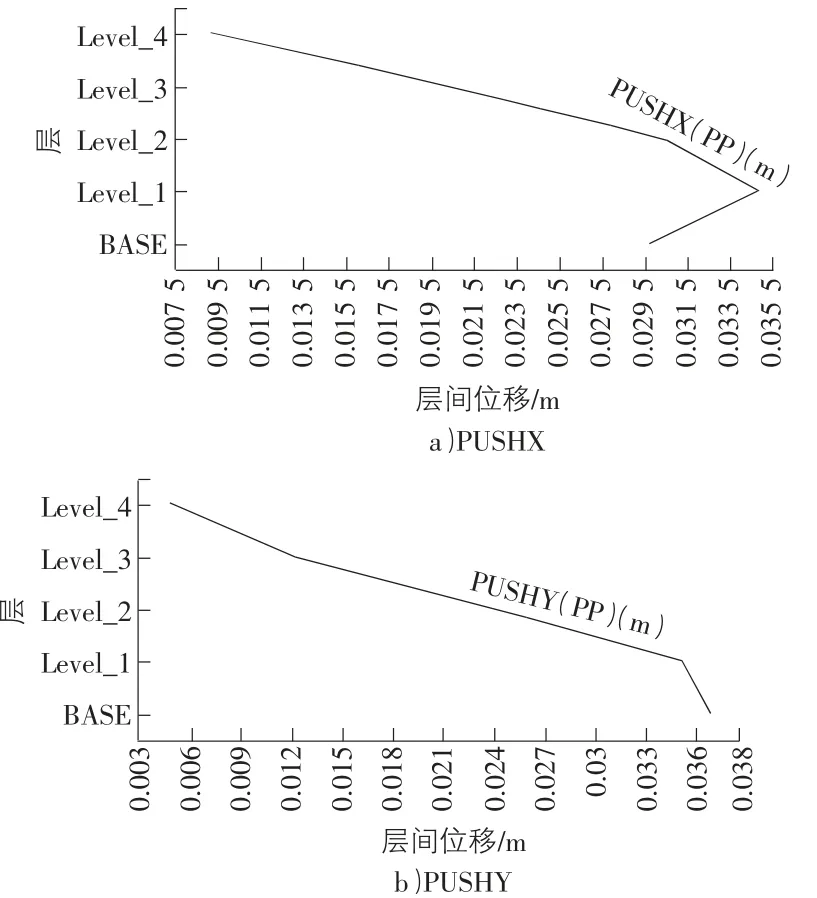
图7 层间位移曲线

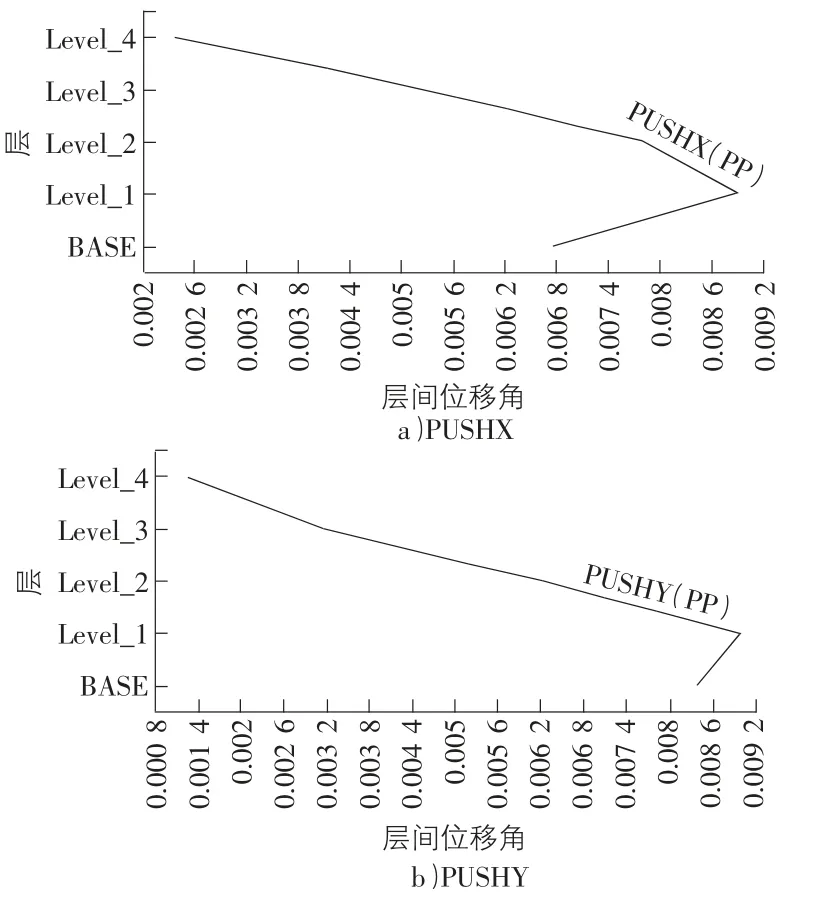
图8 层间位移角曲线

表8 罕遇地震下结构的变形

由上面分析知，在罕遇地震作用下，屈曲约束支撑首先进入出铰耗能，随后梁柱出现塑性铰，其中梁先于柱出铰，整体上结构满足“强柱弱梁”形式，使用屈曲约束支撑能够率先消耗地震能量，大大减小地震力对梁柱的破坏，保护了整体结构，满足大震不倒的抗震设计要求。

5 结语

根据弹性分析和弹塑性分析结果，混凝土框架结构—屈曲约束支撑体系使结构的整体抗震性能得到显著提高。

1)屈曲约束支撑可以为结构提供足够的刚度和承载力。在本工程中采用屈曲约束支撑的方案，能够使各项整体指标均满足规范要求;而没有采用屈曲约束支撑的方案，结构的层间位移角达不到规范要求。

2)该工程选用的屈曲约束支撑满足计算要求，符合小震弹性、中震屈服的设计目标;在罕遇地震下屈曲约束支撑能够继续屈服耗能，构成了结构第一道防线，保护了梁柱，使得梁柱成为第二道防线，满足抗震性能化设计要求。

3)总体上，屈曲约束支撑使结构自重仅仅增加39.893 t，远远小于结构自重(不到0.9%)，屈曲约束支撑易于安装更换，使施工效率显著提高，使综合性效益实现最大化。

［1］GB 50011—2010，建筑抗震设计规范［S］.

［2］汶川地震建筑震害调查与灾后重建分析报告［M］.北京:中国建筑工业出版社，2008.

［3］Jinkoo Kim，Youngil Seo.Seismic design of low-rise steel frames with buckling-restrained braces［J］.Engineering structures，2004，16(5):543-551.

［4］Uang Chia-ming，Nakashima Masayoshi，陆 烨.屈曲约束支撑体系的应用与研究进展(I)［J］.建筑钢结构进展，2005，7(1):1-12.

［5］Xie Q.State of the art of Buckling Restrained Braces in Asia［J］.Journal of construction Steel Research，2005，61(6):39-40.

［6］JGJ 3—2002，高层建筑混凝土结构技术规程［S］.

［7］李国强，胡宝琳，孙飞飞，等.国产TJ 型屈曲约束支撑的研制与试验［J］.同济大学学报，2011，39(5):631-636.

［8］上海蓝科钢结构技术开发公司.TJ 型屈曲约束支撑设计手册［Z］.2010.

［9］解志强.屈曲约束支撑在混凝土框架结构中的工程应用［J］.建筑钢结构进展，2012(10):105-106.

［10］北京迈达斯技术有限公司.midas gen 工程应用指南［M］.北京:中国建筑工业出版社，2012.