改进分解进化算法求解动态火力分配多目标优化模型

张滢，杨任农，左家亮，景小宁，何贵波

（空军工程大学航空航天工程学院，陕西西安710038）

改进分解进化算法求解动态火力分配多目标优化模型

张滢，杨任农，左家亮，景小宁，何贵波

（空军工程大学航空航天工程学院，陕西西安710038）

战前制定合理的火力分配（WTA）方案，可以优化资源配置，用最小的代价获取最大的战场收益。其一，建立了面向多型武器协同进攻作战的动态火力分配（DWTA）多目标优化模型，由多个阶段静态模型构成，各阶段静态模型参数需根据战场态势实时获取；其二，重点研究阶段静态模型求解算法。针对模型特点，设计了一种满足资源约束的编码方式，融合禁忌搜索和拥挤距离策略，提出了一种改进分解进化算法。对比实验验证了算法的可行性、快速性和有效性。

兵器科学与技术；多目标优化；动态火力分配；分解进化算法；禁忌搜索

0 引言

火力分配（WTA）是典型的有约束组合优化问题，具有浓厚的军事应用背景。WTA是指根据作战意图、武器性能等要素，将武器分配用于攻击特定目标的过程。

WTA可划分为静态火力分配（SWTA）和动态火力分配（DWTA）。SWTA只进行一次分配，对应一次攻击，与时间无关。DWTA是一个多阶段分配模型，每个阶段对应一次攻击，前一阶段的决策输出仅作用于该阶段的攻击，下一阶段的决策需根据前阶段的攻击结果进行调整并重新分配。DWTA问题最早由Hosein等［1］提出，近年来对该问题的研究呈上升趋势。建立的模型有基于资产的DWTA模型［1-4］和基于目标的DWTA模型［5-7］，均属于单目标优化模型。资产DWTA模型的目标函数是需保护资产的总存活率，目标DWTA模型的目标函数是攻击目标的总毁伤率。由于涉及需保护的我方资产，这些模型适用于防御型作战。Cai等［8］对WTA问题进行综述，介绍了DWTA的基本概念，对DWTA研究提出了几点展望：建立考虑多型武器协同作战、时间窗口和不确定性等因素的DWTA模型，以及求解这些模型的算法。

WTA属于非确定性多项式（NP）完全问题［9］，理论上可以采用传统的运筹学方法，如分枝定界法、动态规划法等，但算法收敛慢，无法在合理时间内给出满意解，尤其在解决大规模实际问题时更为突出［10-11］。为此，许多学者采用启发式算法求解WTA问题，如遗传算法［12］、免疫算法［13］、粒子群算法［14］，以及融合多种启发式策略的混合算法［2-3，6，15-16］。

为顺应现代战争对快速决策的强烈需求，特别是涉及多型武器协同作战的战役行动，迫切需要研究自动求解WTA问题的模型和方法。为此，本文针对多型武器协同进攻作战的DWTA问题，建立多目标优化模型，结合分解进化和禁忌搜索策略，设计一种求解该模型分解进化的动态火力分配（D-DWTA）算法，并进行仿真测试。

1 DWTA多目标优化模型

定义1 目标时间窗口：目标能被武器攻击的暴露时间。

定义2 武器时间窗口：武器从发现目标到命中目标所需的最短时间，包括武器系统的反应时间和弹药的飞行时间。

DWTA模型由一系列SWTA模型组成，记有s个阶段的DWTA模型为

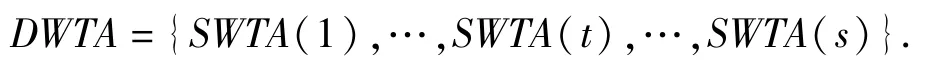
阶段t的决策输出只用于指导该阶段的攻击，需要根据阶段t的攻击结果更新阶段t+1的模型参数。每个阶段SWTA模型只与战场环境进行信息交互，相邻阶段模型不直接关联，如图1所示。

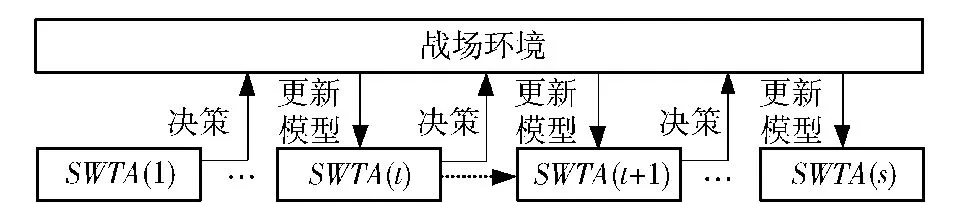
图1 DWTA模型示意图Fig.1 Schematic diagram of DWTA model

考虑在对方领域内进攻作战的DWTA问题，没有需要保护的我方资产。假设在阶段t使用m（t）型武器攻击n（t）个目标，该阶段决策矩阵为（xij（t））n（t）×m（t），xij（t）指阶段t攻击第i个目标需使用j型武器的数量。记

假设1 在每个阶段中允许多种类型武器攻击同一目标。

假设2 在每阶段中每个目标至少分配1枚武器［14］。

多个武器攻击同一目标可能出现攻击冲突。攻击冲突是指前一个武器爆炸造成下一个武器攻击失效的现象。例如，采用2枚电视制导炸弹攻击目标，第1枚炸弹爆炸后目标周边产生烟尘，使得第2枚炸弹无法准确获取目标位置，导致攻击无效。攻击冲突主要是由各武器命中目标的时间差所造成的，避免冲突的有效做法有3种：1）尽量使得所有武器同时命中目标；2）拉开时间差，待爆炸影响消失后再发射下一个武器；3）根据武器特点合理搭配不同类型的武器。如，使用电视制导炸弹和GPS制导炸弹攻击同一目标就不会出现攻击冲突。

定义3 武器攻击冲突因子δ：由武器特性决定。当同时使用多种武器攻击时，若j型武器不会出现攻击冲突，则δ=1，否则δ=0.

假设3 当多个同型武器攻击同一目标，若δj=1，则攻击间隔规定为该型武器的时间窗口；若δj=0，则采取连续攻击方式，尽量使所有武器同时命中目标。

假设4 当多型武器攻击同一目标时，假设每型武器均能在目标暴露的第一时间发现目标，并采取第3种做法避免冲突。

模型参数定义为：

1）δj为j型武器的武器攻击冲突因子；

2）PK（t）=（pkij（t））n×m：pkij（t）∈［0，1］是指在t阶段j型武器攻击i目标的毁伤概率，理论上，在t阶段所有的攻击完成后，i目标的毁伤概率为

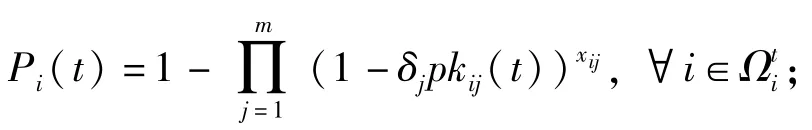
3）Nj（t）：t阶段j型武器的当前可用资产。规定Nj（t）＞0，，为确保模型假设2，需满足；

4）cj：1枚j型武器的成本。攻击i目标需消耗，，则所有攻击的总消耗为；

5）vi（t）：t阶段i目标的价值。在t阶段攻击完成后，从i目标获得的收益为；

考虑收益最大和消耗最小这两个目标函数，则SWTA（t）模型如下：

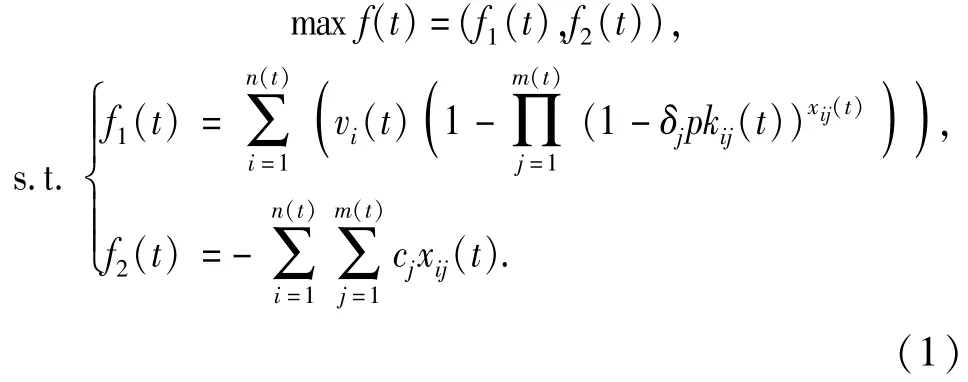
3）时间窗口约束：由模型假设4，为确保武器攻击有效，需满足；

4）xij（t）∈N+，

在t+1阶段，SWTA（t+1）模型可更新的参数有m（t+1）、n（t+1）、PK（t+1）、Nj（t+1）、vi（t+ 1）、ωi（t+1）、.如果我方获取的战场态势信息不足或不明确，将出现不确定性参数，可利用模糊理论修改SWTA（t+1）模型。

2 分解进化多目标优化算法

一般地，多目标优化问题可表述为

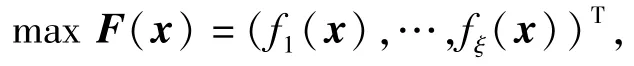
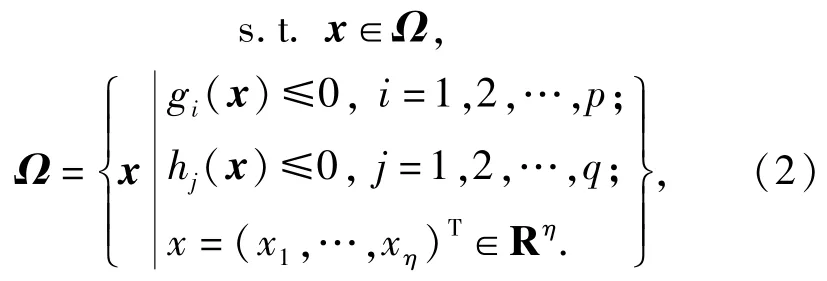
式中：Ω为η维决策空间；（f1，…，fξ）T∈Ψ⊂Rξ为ξ维目标向量；函数F：Ω→Ψ的映射。

MOEA/D算法是由Zhang等［17］于2007年提出的一种较为新颖的算法，是将传统的多目标求解策略与进化算法相结合的优秀范例。算法将ξ个目标函数的优化问题转化为对N个单目标优化子问题的求解。常用的聚合函数构造方法有加权和法、切比雪夫法和边界交集法等。

1）加权和法：对（2）式采用加权和法构造N个单目标优化子问题，则第r（r=1，…，N）个子问题为

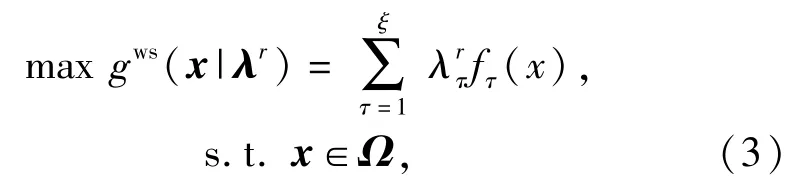
2）切比雪夫法：对（2）式用切比雪夫法构造N个单目标优化子问题，第r（r=1，…，N）个子问题为

定理1 若可行解a*和b*分别是（3）式和（4）式的最优解，则a*和b*是（2）式的Pareto最优解。

证明 反证法。假设a*和b*不是（2）式的Pareto最优解，∃α，β∈Ω，有α≻a*，β≻b*.对于α≻a*，由定义可知［18］，存在集合I1和I2，I1∪I2=｛1，2，…，ξ｝，I1∩I2=Ø且I2非空，使得∀τ∈I1，有fτ（α）=fτ（a*），以及∀τ∈I2，fτ（α）＞fτ（a*）.由于，则，即gws（α|λr）＞gws（a*|λr），这与a*是（3）式的最优解矛盾，因此，a*是（2）式的Pareto最优解。

同理，对于β≻b*，由定义［18］可知，存在集合I1和I2，I1∪I2=｛1，2，…，ξ｝且I2非空，则∀τ∈I1，有fτ（β）=fτ（b*），以及∀τ∈I2，有fτ（β）＞fτ（b*）.而zτ=max｛fτ（x）|x∈Ω｝，则∀τ∈｛1，…，ξ｝，有|fτ（β）-zτ|＜|fτ（b*）-zτ|.且，则gte（β| λr，z）＜gte（b*|λr，z），这与b*是（4）式的最优解矛盾，则b*是（2）式的Pareto最优解。证毕。

因此，通过求解单目标优化子问题，可以得到（2）式的Pareto最优解。

定义3 邻居向量：对于权向量λr∈Rξ，称权向量λs是λr的邻居向量，当且仅当∃θ≥0，满足|λr-λs|≤θ成立。θ值越小，表示权向量λr和λs关系越邻近。

定义4 邻居子问题：称第r个子问题是第s个子问题的邻居子问题，当且仅当对应的权向量λs是λr的邻居向量。一般地，邻居子问题的最优解近似相等。

在MOEA/D算法中，进化种群X=｛x1，x2，…，xr，…，xN｝，其中xr是子问题r的当前最优解。根据邻居关系将进化种群X划分为N个子种群。对∀r∈｛1，…，N｝，将邻居子问题的当前最优解组成子问题r的进化子种群Xr=｛xr1，…，xrT｝.由邻居关系定义可知，越邻近的两个子问题，其目标函数越相近，最优解的相似程度越高。

MOEA/D算法优点在于，用于解决单目标优化问题的算法可以不需修改直接用于求解多目标优化问题，仿真实验表明该算法较其他算法相比，在解的收敛性、均匀性等性能上均表现良好［17，19］。

3 D-DWTA算法

如图1所示的DWTA模型，任何阶段只能确定下一阶段的SWTA模型，后续阶段的SWTA模型参数必须从战场环境实时获取。为此，主要研究阶段SWTA模型的求解算法。（1）式形式的SWTA模型是：1）组合优化问题，其Pareto前沿由若干有限数量的离散点组成；2）约束较为复杂，不易获得可行解；3）就其军事背景而言，对求解算法的速度要求较高，要考虑大规模WTA问题的求解效率。因此，可从以下3个方面对MOEA/D算法进行改进，形成DDWTA算法：

1）收敛速度：模型约束较为复杂，在种群初始化或遗传操作时，经常产生不满足约束的个体，需要花费大量时间重复操作或进行不可行解修复，严重制约算法求解速度。为此，需要合理设计编码方式，尽量减少算法的不可行解修复时间，提高收敛速度。

2）收敛性：定理1在一定程度上确保了MOEA/ D算法的收敛性。然而，在应用分解类进化算法求解某些组合优化问题时，不能保证所有Pareto最优解都是子问题的最优解［20］。也就是说，定理1的逆命题不成立。为此，需在D-DWTA算法中引入某些全局搜索能力强的搜索策略。

3）多样性：MOEA/D算法假设，权向量不同构成的子问题最优解不同。基于这种隐性的种群多样性保持机制，原算法没有采取其他多样性保持策略。对于WTA问题，可以构造无穷个子问题，而Pareto最优解是有限个数。如果仅仅依靠MOEA/D算法的隐性多样性保持机制，可能导致种群过分集中于某些Pareto最优解。为此，需在D-DWTA算法中引入额外的种群多样性保持策略。

3.1 基于资源约束的整数编码

在大规模WTA问题中，满足约束的决策矩阵（xij）n×m为稀疏矩阵。如果直接使用模型的决策变量设计编码，即个体基因型为x=［x11x12…x1mx21…x2m…xn1…xnm］，则在进化时不易得到可行解。

由SWTA模型特点可知，在不考虑弹药补给的情况下，随着阶段t的不断增加，可用武器资产数量不断减少。为此，可设计一种基于资源约束的整数序列编码方式，确保个体满足资源约束。记个体基因型x为

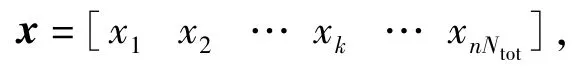
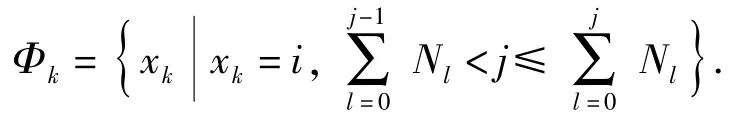
基于资源约束的编码方式认为同一型武器的不同个体在分配时是有区别的（即xk和xij是一种“多对一”的对应关系），实际上增大了搜索空间，但提高了个体出现在可行区域的概率。

3.2 子问题构造

由于模型只有两个目标函数，按照以下方式构造N个均匀分布的权向量［21］：

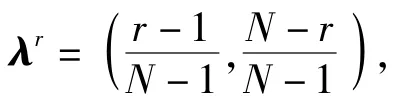
式中：λr∈R2，满足且λr≥0，r=1，2，…，N.随着r的增加，函数f1的重要性将逐渐减小，函数f2的重要性将逐渐增加。

为了消除量纲的影响，对（3）式的第r个子问题的目标函数做如下改进：

3.3 D-DWTA算法描述

算法输入：

1）如（1）式形式的SWTA模型；

2）正整数N：子问题数量；

3）正整数T：子种群规模；

4）终止准则：最大进化代数g_max.

算法输出：

1）PS=｛x1，x2，…｝：非支配个体集合；

2）PF=｛f（x1），f（x2），…｝：近似Pareto前沿。

算法步骤：

步骤1 初始化。

1）初始化进化种群X：随机生成N个可行解，组成进化种群X=｛x1，…，xN｝，置X中个体间最短距离d（X）为无穷大。

3）构造N个子问题：将SWTA模型分解为N个（5）式形式的子问题。为每个子问题随机或按照一定原则分配一个个体，记第r（r=1，…，N）个子问题分配的当前最优解为个体xr.

4）初始化进化子种群：计算任意两个权向量的欧氏距离组成第r个子问题的进化子种群Xr=｛xr1，…，xrT｝.

5）初始化子问题禁忌表：置子问题r的禁忌表为空。

6）初始化非支配解集PS：将X中的非支配个体复制到PS.

步骤2 子问题进化。

1）设置子问题指示符r=1.

2）禁忌搜索生成子代个体yr.

4）更新PS：对于PS中的所有个体，删除被yr支配的个体。如果没有任何个体支配yr，则将yr复制到PS.

5）若d（X）＞0，用yr更新xr，否则转步骤2的第6步。

更新操作：若gws（yr|λr）＞gws（xr|λr），置xr= yr.

6）令r=r+1.若r＜N，转步骤2的第2步，否则转步骤2的第7步。

7）若d（X）＞0，转步骤2的第8步，否则更新种群X.

更新操作：对X∪Y运用NSGA-II算法的快速非支配排序和拥挤距离方法［22］，将前N个最优个体复制到X，并为每个子问题分配X中一个个体。置d（X）为无穷大，转步骤2的第2步。

8）计算d（X）：∀xi，xj∈Xr且i≠j，有

步骤3 终止准则判断。

如果满足终止准则，计算并输出PS和PF，否则转步骤2的第1步。

对算法补充说明：1）步骤2的第8步中‖f（xi）-f（xj）‖表示两个向量的欧拉距离；2）d（X）表示所有进化子种群内个体间最短距离的最小值。若d（X）=0，则进行步骤2的第7步更新种群X，增加种群多样性；3）在子问题进化中引入禁忌搜索策略，如步骤2的第2步，提高全局搜索能力。每个子问题维持一个禁忌表，禁忌对象是子问题的目标函数值，适应度函数为子问题目标函数。当某个子问题的禁忌表已满，但仍需要加入新的禁忌对象，则将禁忌表中的最优对象解禁。对子问题r的禁忌搜索流程为：

1）确定候选解：从子种群Xr中随机选择两个个体，通过单点交叉和标准变异算子产生候选解集。

2）判断候选解的禁忌属性：若候选解集中不存在非禁忌对象，转步骤3，否则令候选解集中非禁忌对象的最佳解为yr，更新禁忌表和“best so far”状态，转步骤4.

3）判断特赦准则：若存在候选解优于问题r的“best so far”状态，则令其为yr，更新问题r的“best so far”状态和禁忌表，否则令yr=xr.

4）结束搜索，输出yr.

D-DWTA算法流程图如图2所示。

4 仿真与分析

实验想定：设有9个目标和7型武器的WTA问题。为统一量纲，将目标价值、武器成本和时间窗口换算为（0，1）之内的小数。模型参数取值如下所示：

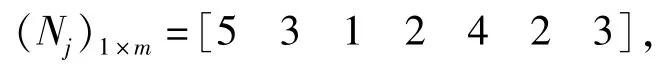
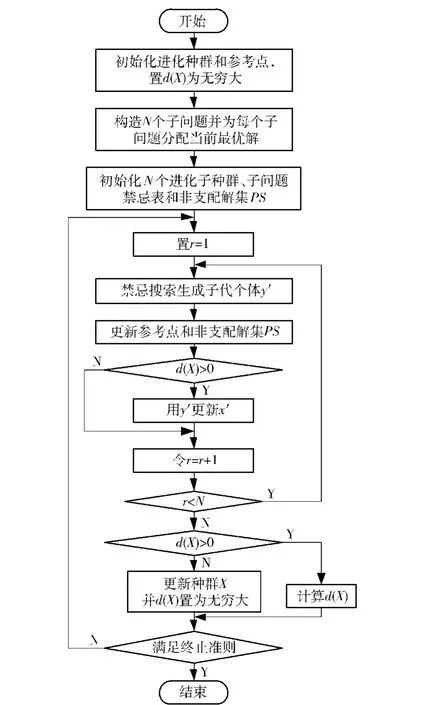
图2 D-DWTA算法流程图Fig.2 Flow chart of D-DWTA algorithm

在酷睿i5、主频2.50 GHz、内存4.0 GB、操作系统Windows7、Matlab2010a环境下进行仿真测试。选取MOEA/D算法［17］和NSGA-II算法［23］与D-DWTA算法进行性能对比。3种算法均采用相同的编码方式，选择、交叉和变异算子，并使用外部种群保存非支配个体。如果进化中产生不满足模型约束的个体，则重复上一步骤，直到得到满足约束的新个体为止。每种算法分别独立运行30次。

定义5 每代相对C值：假设PSg_max是最终输出的近似Pareto最优解集，PSg是第g代进化后得到的近似Pareto最优解集，则每代相对C值定义为

式中：di是集合PSg中每个个体距离集合PSg_max的最小归一化欧式距离。∀ai∈PSg：

4.1 收敛速度分析

参数设置：禁忌搜索的候选解集规模为4，禁忌长度为3，禁忌表长度为20，子种群规模为5.为叙述方便，将MOEA/D算法、NSGA-II算法和D-DWTA算法简记为算法M、算法N和算法D，平均运行时间如表1所示。

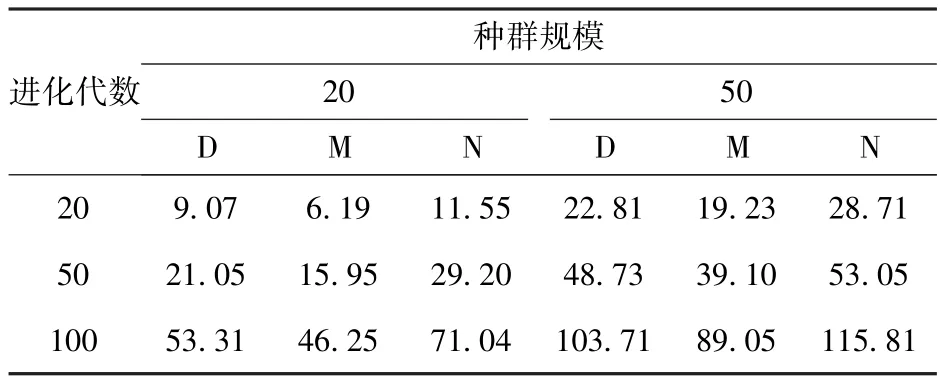
表1 平均运行时间Tab.1 Mean operating times

参数设置：种群规模为20，最大进化代数为100，其他参数不变。计算得出3种算法的平均每代相对C值与进化代数的关系如图3所示。

D-DWTA算法的禁忌搜索和拥挤距离策略增加了计算量，使得D-DWTA算法不是3种算法中运行时间最短的，但是收敛速度最快的。当进化到13代时，D-DWTA算法的平均相对C值为0.019，非常接近算法最终的近似Pareto最优解集。

图3 平均每代相对C值对比Fig.3 Mean C value of each generation

4.2 收敛性和多样性分析

参数设置：禁忌搜索的候选解集规模为4，禁忌长度为3，禁忌表长度为20，种群规模为20，子种群规模为5，最大进化代数为100.采用两个集合C值［23］和S值［18］分别衡量3种算法的收敛性和多样性，用盒图表示统计结果，如图4和图5所示。

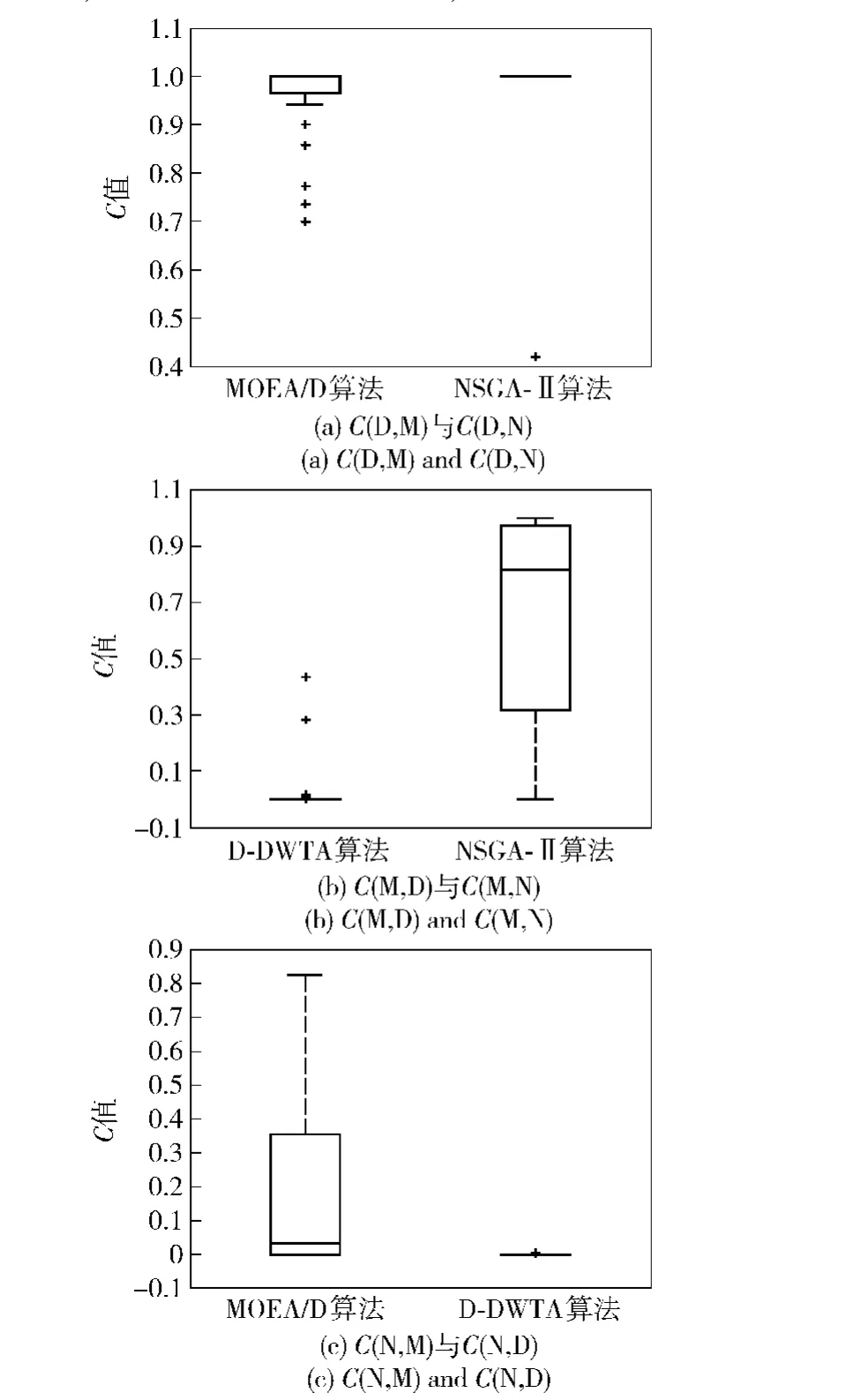
图4 3种算法的C值统计特性Fig.4 C value statistical properties of 3 algorithms

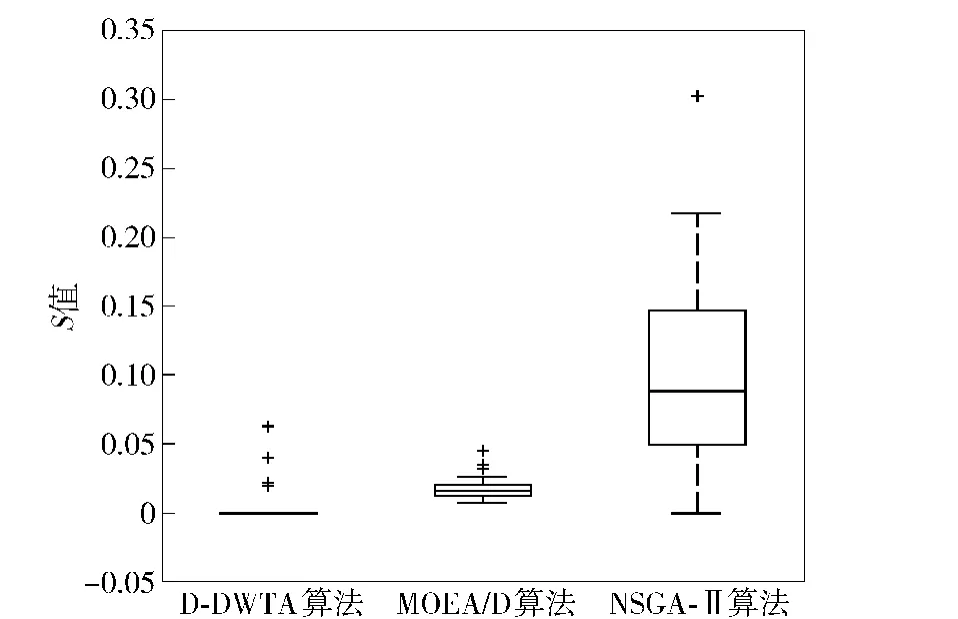
图5 3种算法的S值统计特性Fig.5 S value statistical properties of 3 algorithms

实验结果表明，与MOEA/D和NSGA-II算法相比，D-DWTA算法求解WTA实验想定得到的近似Pareto最优解集是最优的，分布是最均匀的。

5 结论

本文为解决多型武器协同进攻作战DWTA问题，建立了由多阶段SWTA模型构成的DWTA模型。设计了满足资源约束的编码方式缩短不可行解修复时间，提高算法求解速度。在分解进化算法框架下，引入禁忌搜索和拥挤距离策略，提高了D-DWTA算法的收敛性和多样性。为测试算法效率，与MOEA/D和NSGA-II算法进行对比。从仿真结果可知，D-DWTA算法的求解速度不是最快的，但收敛速度最好，得到的近似Pareto最优解是最优、分布最均匀的。本文对DWTA模型的求解思路是，通过求解各阶段SWTA模型最优解得到DWTA模型的相对较优解，下一步工作需设计全阶段最优求解算法。实验中为减小求解难度，所有武器都不存在攻击冲突，即δj=1，j=1，2，…，7，这对武器性能要求比较高，需设计更为合理的实验想定测试算法效率。此外，考虑不确定因素的DWTA模型及其求解方法将是下一阶段研究内容。

（

）

［1］Hosein P A，Athans M.Preferential defense strategies，part II：the dynamic case，LIPS-P-2003［R］.Cambridge，UK：MIT，1990.

［2］Tokgöz A，Bulkan S.Weapon target assignment with combinatorial optimization techniques［J］.International Journal of Advanced Research in Artificial Intelligence，2013，2（7）：39-50.

［3］Xin B，Chen J，Zhang J，et al.Efficient decision makings for dynamic weapon-target assignment by virtual permutation and tabusearch heuristics［J］.IEEE Transactions on Evolutionary Computation，2010，40（6）：649-662.

［4］Xin B，Chen J，Peng Z H，et al.An efficient rule-base constructive heuristic to solve dynamic weapon-target assignment problem［J］.IEEE Transactions on Evolutionary Computation，2011，41（3）：598-606.

［5］Hosein P A，Athans M.Some analytical results for the dynamic weapon-target allocation problem，LIPS-P-1944［R］.Cambridge，UK：MIT，1990.

［6］Leboucher C，Shin Hyo-Sang，Siarry P，et al.A two-step optimisation method for dynamic weapon target assignment problem［EB/ OL］.US：INTECH，2013［2015-03-09］.http：∥dx.doi.org/ 10.5772/53606.

［7］Havens M E.Dynamic allocation of fire and sensors［D］.Monterey，CA，US：Naval Postgraduate School，2002.

［8］Cai H P，Liu J X，Chen Y W，et al.Survey of the research on dynamic weapon-target assignment problem［J］.Journal of Systems Engineering and Electronics，2005，17（3）：559-565.

［9］Lloyd S P，Witsenhausen H S.Weapon allocation is NP-complete［C］∥Proceedings of IEEE Summer Simulation Conference.Reno，NV，US：IEEE，1986：1054-1058.

［10］Ravindra K A，Arvind K，Krishna C J，et al.Exact and heuristic algorithms for the weapon-target assignment problem［J］.Operations Research，2007，55（6）：1136-1146.

［11］Sikanen T.Solving weapon target assignment problem with dynamic programming，Technology Report 55670［R］.［2014-01-10］.http：∥www.sal.tkk.fi/Optinnot/Mat-2.108/pdf-files/esik08b.pdf.

［12］Bryant A J.String-and permutation-coded genetic algorithms for the static weapon-target assignment problem［C］∥Proceedings of the Genetic and Evolutionary Computation Conference.Montral，Canada：IEEE，2009：2553-2558.

［13］阮旻智，李庆民，刘天花.编队防空火力分配建模及其优化方法研究［J］.兵工学报，2010，31（11）：1525-1529. RUAN Min-zhi，LI Qing-min，LIU Tian-hua.Modeling and optimization on fleet antiaircraft firepower allocation［J］.Acta Armamentarii，2010，31（11）：1525-1529.（in Chinese）

［14］刘晓，刘忠，侯文姝，等.火力分配多目标规划模型的改进MOPSO算法［J］.系统工程与电子技术，2013，35（2）：326-330. LIU Xiao，LIU Zhong，HOU Wen-shu，et al.Improved MOPSO algorithm for multi-objective programming model of weapon-target assignment［J］.Systems Engineering and Electronics，2013，35（2）：326-330.（in Chinese）

［15］Leboucher C，Shin Hyo-Sang，Stephane L M，et al.Novel evolutionary game based multi-objective optimisation for dynamic weapon target assignment［C］∥19th World Congress of the International Federation of Automatic Control.Cape Town，South Africa：International Federation of Automatic Control，2014：3936-3941.

［16］丁铸，马大为，于存贵，等.基于禁忌搜索与微粒群优化算法的混合优化策略算法在目标分配问题上的应用［J］.兵工学报，2007，28（9）：1127-1131. DING Zhu，MA Da-wei，YU Cun-gui，et al.Application of hybrid optimization strategy algorithm based on tabu search and particle swarm optimization algorithms for weapon-target assignment problems［J］.Acta Armamentarii，2007，28（9）：1127-1131.（in Chinese）

［17］Zhang Q F，Li H.MOEA/D：a multiobjective evolutionary algorithm based on decomposition［J］.IEEE Transactions on Evolutionary Computation，2007，11（6）：712-731.

［18］公茂果，焦李成，杨咚咚，等.进化多目标优化算法研究［J］.软件学报，2009，20（2）：271-289. GONG Mao-guo，JIAO Li-cheng，YANG Dong-dong，et al.Research on evolutionary multi-objective optimization algorithms［J］.Journal of Software，2009，20（2）：271-289.（in Chinese）

［19］Li H，Zhang Q F.Multi-objective optimization problems with complicated pareto sets，MOEA/D and NSGA-II［J］.IEEE Transactions on Evolutionary Computation，2009，2（3）：284-302.

［20］Ehrgott M，Gandibleux X.A survey and annotated bibliography of multiobjective combinatorial optimization［J］.OR Spectrum，2000，22（4）：425-460.

［21］Mei Y，Tang K，Yao X.Decomposition-based memetic algorithm for multiobjective capacitated arc routing problem［J］.IEEE Transactions on Evolutionary Computation，2011，15（2）：151-165.

［22］Deb K，Pratab A，Agarwal S，et al.A fast and elitist multi-objective genetic algorithm：NSGA-II［J］.IEEE Transactions on Evolutionary Computation，2002，2（6）：182-197.

［23］Zitzler E，Thiele L.Multiobjective evolutionary algorithms：a comparative case study and the strength Pareto approach［J］. IEEE Transactions on Evolutionary Computation，1999，3（4）：257-271.

Improved Decomposition-Based Evolutionary Algorithm for Multi-objective Optimization Model of Dynamic Weapon-target Assignment

ZHANG Ying，YANG Ren-nong，ZUO Jia-liang，JING Xiao-ning，HE Gui-bo
（Aeronautics and Astronautics Engineering Institute，Air Force Engineering University，Xi'an 710038，Shaanxi，China）

A reasonable weapon-target assignment（WTA）scheme is developed to optimize the allocation of limited resources，which brings the maximum awards with minimum costs.A dynamic weapon-target assignment（DWTA）multi-objective optimization model is established，especially for the offensive operation with multi-weapon.The proposed model is composed of several stage static models.The parameters of each stage model are obtained from the battlefield in real time.An algorithm is elaborately studied to solve the stage model based on the hypothesis to deal with the dynamic model.According to the characteristic of the proposed model，an encoding mode is constructed to satisfy the resource constraints.An improved decomposition-based evolutionary algorithm is proposed by mixing of tabu search and crowding distance strategies.Comparative experiments prove that the proposed algorithm is feasible，fast and efficient.

ordnance science and technology；multi-objective optimization；dynamic weapon-target assignment；decomposition-based evolutionary algorithm；tabu search

TP391

A

1000-1093（2015）08-1533-08

10.3969/j.issn.1000-1093.2015.08.022

2014-04-22

张滢（1988—），女，博士研究生。E-mail：zhangying1988@126.com；杨任农（1969—），男，教授，博士生导师。E-mail：cmproof@gmail.com