机动目标拦截含攻击角约束的新型滑模制导律

张尧，郭杰，唐胜景，商巍，张浩强

（北京理工大学宇航学院飞行器动力学与控制教育部重点实验室，北京100081）

机动目标拦截含攻击角约束的新型滑模制导律

张尧，郭杰，唐胜景，商巍，张浩强

（北京理工大学宇航学院飞行器动力学与控制教育部重点实验室，北京100081）

针对导弹带有攻击角约束的机动目标拦截问题，结合积分滑模和全局滑模控制方法的优点，设计了一种全新的导弹滑模制导律（SMGL）。在纵向平面内建立考虑攻击角约束的弹目相对运动方程。采用一种新的非线性饱和函数来构造积分滑模面中的积分项，提出了一种新型的非线性全局积分滑模控制方法，解决了传统积分滑模控制中系统暂态性能恶化的问题，降低了系统的稳态误差，保证导弹在有限时间内以更理想的攻击角命中目标，同时使导弹在整个拦截过程中具有很强的鲁棒性。采用动态面控制方法设计了考虑攻击角约束和自动驾驶仪动态特性的导弹全局非线性积分SMGL，基于Lyapunov稳定性准则证明了闭环系统所有状态最终一致有界。与传统线性积分SMGL和偏置比例导引律进行仿真对比，仿真结果验证了全局非线性积分SMGL的有效性和优越性。

飞行器控制、导航技术；制导律；全局非线性积分滑模；动态面控制；攻击角约束

0 引言

在导弹制导与控制系统设计过程中，制导律的设计起着重要的作用。为了实现在战场中对目标的精确打击，制导律在攻击末端追求很小的脱靶量。然而，随着精确制导技术的不断发展，在制导律的设计过程中，除了需要考虑脱靶量的约束外，在许多打击任务中还需要对导弹制导末端的攻击角进行约束，从而在对目标实施打击时发挥战斗部的最大效能，以达到最佳的毁伤效果。

当目标无机动、自动驾驶仪视为理想环节且控制能量受限时，传统的比例导引律可以获得较好的打击效果。但在打击机动目标时，比例导引律很难达到满意的效果。随着控制理论的发展，针对含攻击角约束的拦截打击问题，相关研究在原有制导律设计思想的基础上提出了新的制导律设计方法，如新型比例导引［1-5］、最优制导律［6-12］、滑模制导律（SMGL）［13-16］等。基于传统的比例导引律，Zhang等［1］提出了一种考虑攻击角约束的偏置比例导引律（BPNGL），同时加入了对剩余时间误差的反馈环节，实现了导弹在时间和攻击角双重约束下对机动目标的有效打击。Byung等［2］针对角度约束下的制导问题研究了一种新型的BPNGL，同时，针对三维空间内考虑攻击角约束的超声速拦截问题。Lu等［3］采用自适应变系数策略对传统比例制导律进行了改进。此外，文献［4］基于平面弹道的几何特征设计了具有末端攻击角约束的圆周轨迹制导律，在此基础上，胡锡精等［5］提出了一种具有碰撞角约束的三维圆轨迹制导律。总体来讲，传统的制导律通过对相应技术的改进，使导弹在拦截非机动目标时弹道性能好，脱靶量小，在满足制导任务的基础上易于工程实现。但其前向攻击能力差，对打击机动目标，末端脱靶量较大，无法精确满足攻击角和制导精度的要求。随着20世纪70年代初现代控制理论的盛行，人们逐渐将传统制导律设计与现代控制理论相结合。自Kim等［6］首次提出考虑攻击角约束的最优制导律以来，很多学者针对不同的应用背景，基于最优控制理论提出了多种依据不同性能指标的具有末端角度约束的最优制导律。Idan等［7］在目标轨迹已知的前提下对于导弹打击机动目标考虑终端落角约束的问题设计了平面运动的最优制导律。Song等［8］以时间最短为性能指标，基于极大值原理设计了含末端弹道倾角限制的Bang-Bang最优制导律。Song等［9］针对变速导弹在垂直平面内打击机动目标的问题提出了一种考虑攻击角约束的最优制导律。文献［10］讨论了采用广义矢量形式的显示含落角约束的最优制导算法。Zhang等［11］利用最优控制方法通过以脱靶量和终端落角为约束针对地面目标设计了三维制导律，通过求解Riccati方程对任意阶系统进行降阶。此外，不少学者在原有最优制导律基础上，结合微分对策理论，提出了双方动态控制的微分对策制导律，使系统的综合性能最优。Shaferman等［12］基于线性二次型理论提出了一种考虑终端落角约束的微分对策制导律。微分对策制导律虽优于比例导引律和最优制导律，但在求解微分对策过程中遇到了两边编制问题，需要采用极小值定理，很难得到解析解，制导律的设计存在较大的保守性。同时，上述制导律的设计均需要完全已知制导过程中目标运动的精确模型以及准确估算导弹运动的剩余时间，状态信息准确度越高，所设计的制导律命中精度就越高。但在实际应用过程中，很多目标的状态信息无法准确测量，尤其是目标加速度，存在很大的估计误差，从而导致此类制导律的工程应用受限。

滑模变结构控制是一种对系统参数摄动和外界干扰等系统不确定性具有很好鲁棒性和稳定性的控制方法。在导弹的制导律设计时，设计者通常以弹目视线角速率或脱靶量作为变量设计滑模面，通过设计导弹的需用过载使所设计的滑模面在有限时间内快速收敛于0，从而实现导弹对目标的有效打击。由于所设计的控制量中变结构控制切换项能够补偿系统中的不确定性，故SMGL因其不用严格依赖目标运动的精确模型而被广泛应用。Sachit等［13］基于零化视线角速率理论，针对水平面内考虑攻击角约束打击机动目标的问题，设计了传统意义上的SMGL.Lee等［14］考虑制导过程中的落角约束，通过构造特征函数提出了一种高性能的SMGL，对所设计的制导律的参数整定问题提出了采用极点配置的整定方法。但是，该制导律对落角约束的设计只是针对固定或低速目标。窦荣斌等［15］通过采用2阶滑模控制思想设计了再入飞行器的末制导律，但在制导末期容易产生控制量的高频颤振。熊俊辉等［16］针对迎击拦截高超声速目标的问题，应用模糊变系数策略设计了一种复合SMGL，降低了制导初期的需用法向过载。但是，由于目标运动的机动性过大，在传统的SMGL拦截机动目标的末制导段，会不可避免地产生导弹需用过载过大或产生振荡，同时也会使导弹在打击任务末期的攻击角不理想。因此，有必要对现有的SMGL进行改进，提出一种针对机动目标拦截的新型SMGL.

众所周知，在传统滑模控制中，当系统存在不确定性和外界扰动时，为了抑制控制量颤振而引入的边界层方法会导致系统状态存在稳态跟踪误差。因此，在滑模面的设计中可以引入积分项来抑制系统的稳态误差，增强系统的鲁棒性。但是，当系统状态的初始误差较大时，积分滑模会导致系统状态存在大的超调和长的调节时间，从而恶化系统的暂态性能。尤其是，当执行机构饱和时，滑模面的积分项会产生积分Windup效应，甚至使系统不稳定［17］。此外，由于传统滑模控制只有在系统状态保持滑模运动阶段时才具有很强的鲁棒性，无法保证系统在全过程中都具有鲁棒性。针对上述不足，本文采用一种新的非线性饱和函数来设计非线性积分滑模面，从而改善系统的暂态性能，减小系统的稳态误差。与此同时，将非线性积分滑模控制（NISMC）方法和全局滑模控制（GSMC）方法［18］的优点相结合，在保证系统暂态性能和小稳态误差的基础上，消除了滑模控制中系统状态在有限时间内从任意初始状态值运动到滑模面的这一阶段，使系统状态在一开始就处于滑动模态，克服了传统滑模控制中的到达阶段不具备鲁棒性的缺点，从而使系统在全局具有强鲁棒性。

在实际工程应用中，当目标机动时，自动驾驶仪的动态特性会对导弹的制导精度造成很大影响。因此，在制导律设计过程中考虑自动驾驶仪动态特性具有十分重要的意义。Chen等［19］和Zhang等［20］均将自动驾驶仪视为1阶惯性环节，并利用最优控制和滑模控制方法对导弹的制导律进行设计。而实际的导弹自动驾驶仪具有高阶动态特性，采用2阶动态特性来描述更为合理。文献［21］结合反馈线性化技术，采用Backstepping方法，考虑到自动驾驶仪动态特性补偿和末端攻击角约束，提出了一种反演递推制导律。在考虑自动驾驶仪动态特性的制导律设计过程中，若采用Backstepping方法设计制导律会含有对视线角速率的2阶导数，工程中不易获得，从而增加了系统设计的复杂度［22］。为了解决上述不足，相关文献［23-24］采用动态面控制方法有效地实现了对视线角速率2阶或高阶导数的实时估测，从而解决了Backstepping方法中的“微分膨胀”问题。

本文基于纵向平面内的弹目相对运动方程，考虑自动驾驶仪2阶动态特性，针对拦截机动目标的攻击角约束问题，应用全局NISMC方法和动态面控制方法，提出了一种全新的导弹全局非线性积分滑模制导律（GNISMGL）利用这种制导律，改善了制导过程中系统的暂态性能，减小了制导末端攻击角的稳态误差，保证了导弹在整个制导过程中具有很强的鲁棒性。

1 问题描述与数学模型

如图1所示，建立纵向平面内拦截过程中弹目相对运动的几何关系。图中：M和T分别为导弹和目标的质心位置；vM和vT分别为导弹和目标的运动速度；aM和aT分别为导弹和目标运动的法向加速度；θM和θT分别为导弹运动的弹道倾角和目标运动的航迹角；q为弹目相对运动的视线角；r为导弹与目标的相对距离。由图1可得纵向平面内的弹目相对运动方程：

图1 纵向平面内弹目相对运动Fig.1 Planar relative motion of missile and target

（2）式两边同时对时间t求导，可得

为方便研究，作出如下假设：

1）目标的法向加速度aT和切向加速度是有界的，且在任意t时刻满足，其中d1和d2为目标加速度的上界。

攻击角为拦截末端导弹的速度矢量和目标的速度矢量之间的夹角。所以，考虑到对攻击角的约束就需要严格限制导弹命中目标（脱靶量为0）时刻的弹道倾角。定义制导结束时刻为tf，导弹期望的攻击角为θd，制导结束时刻所期望的视线角为qd，则考虑攻击角约束的制导律设计问题是指在导弹以零脱靶量命中目标的同时以期望的攻击角对目标实施打击，即

（8）式表明导弹命中目标时目标在导弹的导引头视场范围内，由（2）和（6）式可得

由（7）式可知，如果已知制导结束时刻目标的航迹角θT（tf），对于所期望的导弹攻击角θd，命中时刻存在唯一的导弹弹道倾角θM（tf）与之对应，继而由（6）式和（8）式可得制导结束时刻的期望视线角qd.因此，考虑攻击角约束的制导律设计问题就成了设计合适的制导指令，使弹目相对运动的终端视线角满足q（tf）=qd.

如果已知θT（tf）和qd，那么存在唯一的θM（tf）满足（6）式～（8）式。

2 考虑攻击角约束的导弹GNISMGL设计

在制导律设计之前，首先引入滑模控制中关于有限时间稳定性的定义和判别准则。

定义1［25］考虑如下系统：

式中：f（x）:D→Rn是定义在D上取值于n维空间Rn且满足局部Lipschitz连续性函数。对于所考虑的系统（10）式，f（x）:U→Rn为半开域U上对x连续的函数，且半开域U包含原点。有限时间收敛是对∀x0∈U0⊂Rn，存在一个连续函数T（x）:U0｛0｝→（0，+∞），使得系统（（10）式）的解x（x0，t）满足：当t∈［0，T（x0）］时，存在x（x0，t）∈U0｛0｝和；当t＞T（x0）时，存在x（x0，t）= 0.假设系统（（10）式）的平衡点为x=0，当且仅当系统是强稳定的且有限时间收敛的，系统的平衡点x=0为有限时间稳定。若U=U0=Rn，则平衡点全局有限时间稳定。

引理1［25］对于系统（（10）式），假设存在连续的可微函数V:U→R满足下列条件：

1）V是正定函数；

2）存在正实数c＞0和0＜α＜1，以及一个包含原点的开邻域，使得条件，成立。

则系统（（10）式）是有限时间稳定的。收敛时间T与系统状态的初始值x（0）=x0有关，收敛时间的上界为，其中x0为原点某一开邻域内的任意一点。若且V（x）为径向无界的，则系统（（10）式）是全局有限时间稳定的。

假设导弹的自动驾驶仪为理想环节，则aM= ac，ac为制导过程中导弹运动的法向加速度指令。取状态变量x1=q，，则制导系统的状态方程可以写成如下形式：

为了克服传统积分滑模控制的缺点，改善执行机构饱和时制导系统的暂态性能，减小制导末端攻击角的稳态误差，同时弱化初始条件对系统暂态性能的影响，保证导弹在整个制导过程中都具有很强的鲁棒性。构造如（12）式的全局非线性积分滑模面：

式中：e为制导过程中实际视线角和期望视线角之间的误差，e=q-qd，；KP、KI和η为大于0的设计参数；g（e）为一类具有“小误差放大、大误差饱和”功能的非线性光滑连续函数。为了保证系统的初始状态位于滑模面上，当t=0时，S（0）=0，取

为了说明函数g（e）的特性，引入如下形式的类势能函数［17］：

将（13）式对自变量e求导，可得

式中：φ＞0为误差成型参数。非线性连续函数G（e）和g（e）的函数曲线如图2所示。

图2 类势能函数及其导数的曲线（φ=1）Fig.2 Curves of quasi potential energy function and its derivative（φ=1）

引理2［17］非线性连续函数G（e）和g（e）具有如下性质：

1）若e≠0，则G（e）＞0；若e=0，则G（e）= g（e）=0；

2）G（e）为连续二次可微函数，当|e|＜φ时，g（e）是严格单调递增函数，当|e|≥φ时，g（e）为饱和函数。

由图2可以看出：当系统误差e小于误差成型参数φ时，|g（e）|≥|e|；当系统误差e大于φ时，|g（e）|＜|e|.图2形象地说明了所设计的非线性函数g（e）具有“小误差放大、大误差饱和”的作用。通过选择不同的误差成型参数φ来获得期望的误差状态，从而保证弹目相对运动的视线角q更加趋近于期望视线角qd.

将（12）式改写成（15）式：

对于所构造的全局非线性积分滑模面（（15）式）中的参数选择而言，增大KP可以有效地减小滑模面偏差，但另一方面，KP影响滑模面变化的稳定性，过大的KP会造成滑模面不能稳定收敛，系统状态发散；增大KI可以有效地减小滑模面收敛时的稳态误差，而过大的KI会使滑模面收敛过程中调节时间过长。因此，在设计时必须合理地选取KP、KI和η，使得S=0.

定理1 对于（11）式所描述的制导系统，取（15）式形式的全局非线性积分滑模面，在满足引理1和引理2的基础上，令切换增益，如果考虑攻击角约束的导弹GNISMGL中导弹的法向加速度指令满足：

证明：对（15）式求导可得

将（11）式、（16）式和（17）式代入（18）式中有

构造Lyapunov函数：

将V1对时间t求导后，可得

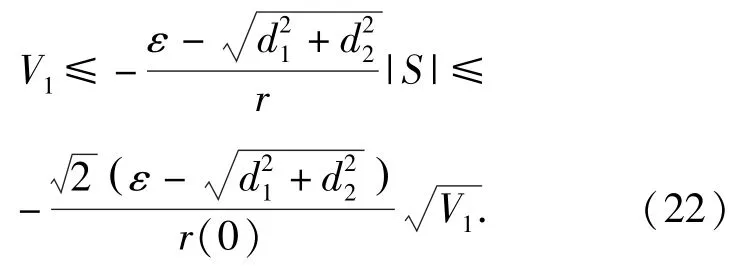
由引理1可知，（22）式表明：系统（（11）式）有限时间稳定，视线角误差e=q-qd在有限时间内收敛至全局非线性积分滑模面（（15）式）.设视线角误差e收敛至滑模面的时间为T1，由引理1可得

（23）式证明了当存在外界扰动时滑模面始终收敛于边界层内，消除了到达过程，视线角误差e和视线角速率误差在初始时刻就落在滑模面（（15）式）上。

至此，证明了视线角误差和视线角速率误差均能够渐进收敛于0，即视线角速率能够在有限时间内渐进收敛于0，同时视线角q能够在有限时间内渐进收敛于期望视线角qd.由（15）式可知：

（25）式表明滑模面S经过一段时间T1后能够渐进收敛于S=0.由此定理1得证。

定理2 对于系统（（11）式），取（12）式形式的滑模面，当导弹命中目标时，视线角误差满足

证明：由（19）式可知，令

则

对（28）式两边同取拉氏变换，有

式中：ζ为Laplace算子。根据终值定理有

因为

构造Lyapunov函数为

（34）式沿（32）式求导得

即

3 考虑自动驾驶仪动态特性和攻击角约束的导弹GNISMGL设计

3.1 制导律设计

在实际制导过程中，自动驾驶仪通过产生相应的控制力或控制力矩对制导回路产生的过载指令进行跟踪，但导弹实际产生的过载和过载指令之间存在一定的滞后，从而影响制导精度。因此，研究考虑自动驾驶仪动态特性的制导律具有一定的实际意义。

将具有高阶动力学特性的自动驾驶仪近似成2阶动态环节：

式中：aM为制导过程中导弹实际的法向加速度；u为制导回路产生的法向加速度指令；ξ和ωn分别为导弹自动驾驶仪的阻尼比和固有频率。

定义两个新的状态：x3=aM和.联立（11）式和（40）式有

针对非线性时变系统（（41）式），结合全局非线性积分滑模控制方法和动态面控制方法，设计考虑攻击角约束和自动驾驶仪动态特性的制导律。

动态面控制方法是一种在Backstepping和多面滑模控制基础上发展而来的控制方法［22］。这种方法在制导律设计中的应用避免了对模型状态变量——视线角速率的2阶微分，克服了Backstepping中的“微分膨胀”问题，而且不需要对系统干扰项的光滑性进行约束，降低了整个系统设计的复杂度。

步骤1 设计x3虚拟控制量.

定义第1个动态面为

将S1对时间t求导，有

式中：K2为正实数。将通过一个时间常数为τ3＞0的一阶低通滤波器，可得滤波后的虚拟控制量x3d：

步骤2 设计x4的虚拟控制量

定义第2个动态面为

将S2对时间t求导，有

选择虚拟控制量x4，使S2→0：

式中：K3为正实数。将通过一个时间常数为τ4＞0的1阶低通滤波器，可得滤波后的虚拟控制量x4d：

步骤3 设计实际控制量u.

定义第3个动态面为

将S3对时间t求导，有

设计实际控制量u，使S3→0：

因此，实际控制量u为

至此，考虑自动驾驶仪动态特性和攻击角约束的导弹GNISMGL设计完成。（53）式即为最终制导回路生成的法向加速度指令。

3.2 稳定性分析

下面对所设计的GNISMGL作用下的闭环系统稳定性进行证明。

首先，定义如下边界层误差：

将（54）式和（55）式分别代入（46）式和（50）式中，有

选取闭环系统的Lyapunov函数为

将（58）式对时间t求导，有

式中：由Young不等式ab≤a2/2+b2/2可得

考虑到（1）式～（4）式中的相关参数及其导数均有界，经计算可得

式中：χ3和χ4均为连续正值函数。给定任意正数κ，存在集合Bκ=｛（S1，S2，S3，y3，y4）T:V≤κ｝为一个紧集。因此，连续函数χ3和χ4在Bκ上有最大值，分别记为M3和M4.其中M3由KP、KI、K2和ε决定，而M4则由KP、KI、ε、K2、K3和τ3决定。由此可得。

由上面分析可知：

式中：α为一正数，则有

因此，S1、S2、S3、y3和y4均一致最终有界，继而x1、x2、x3、x4、x3d、x4d、x3、x4也一致最终有界。对于任意选定的KP、KI、η和ε，当选定的设计参数Ki（i=2，3，4）足够大，且τi（i=3，4）足够小，则α将足够大，那么就可以使ρ/α任意小。这意味着，可以使S1最终有界任意小，即视线角误差e和视线角速率误差均最终有界任意小。

综上所述，可以得到如下定理。

定理3 考虑在引理1和引理2约束下的系统（（41）式）和所设计GNISMGL产生的法向加速度指令（（53）式）所组成的闭环系统。对于任意选定的KP、KI、η和ε，当选定的设计参数Ki（i=2，3，4）足够大，且τi（i=3，4）足够小，可以使S1最终有界任意小，即视线角误差e和视线角速率误差e·均最终有界任意小。

4 仿真结果

为了验证本文所提的考虑攻击角约束和自动驾驶仪动态特性的导弹GNISMGL的有效性和优越性，本节针对导弹拦截机动目标的末制导段进行数值仿真。

仿真实验中，导弹和目标均在铅垂平面内运动，仿真步长为0.01 s.导弹初始位置为xM（0）=0 m，yM（0）=0 m；目标初始位置为xT（0）=4 330 m，yT（0）=2 550 m.假设末制导段导弹无推力作用，即，导弹飞行速度为vM=600 m/s，初始弹道倾角为θM（0）=60°，导弹自动驾驶仪阻尼比为ξ=0.5，固有频率为ωn=10 rad/s；期望视线角qd= 20°；目标的初始速度为vT（0）=300 m/s，初始航迹角为θT（0）=0°，g=9.8 m/s2.对于目标的机动性分以下两种情况进行仿真分析。

算例2 目标做非周期性机动，即

所设计的考虑攻击角约束和自动驾驶仪动态特性导弹GNISMGL的参数设计为KP=1.5，KI=1，η=5，φ=0.003，ε=70，K2=6 000，K3=10，K4=10，τ3=τ4=0.01.

同时，为了进一步说明本文GNISMGL的优越性，将该方法与传统线性积分滑模制导律［27］（LISMGL）和BPNGL进行对比。BPNGL所生成的法向加速度指令为.对于LISMGL的设计，选取如下滑模面：

则LISMGL所生成的法向加速度指令为

同样，考虑自动驾驶仪动态特性设计导弹的LISMGL，选择LISMGL参数为k1=8，k2=12，ε=70，其余参数与上文所述相同。

为了抑制符号函数对SMGL律带来的控制量高频颤振问题，对其进行光滑处理，采用如（73）式所示连续饱和函数代替制导律中的符号函数sgn（·）.

式中：δ为消颤因子，仿真中取δ=0.001.

图3为拦截过程中弹目相对运动曲线。对于拦截两类机动目标，从整体上看，GNISMGL和LISMGL由于均采用了积分滑模方法，二者作用下的导弹运动轨迹存在一定的相似性。与BPNGL相比，在保证有效打击的前提下，GNISMGL使导弹的拦截时间更短，攻击角更为理想。

图4和图5分别为制导过程中弹目相对运动的视线角速率和视线角变化曲线。从图4和图5中可以看出：当目标机动运动时，GNISMGL能够保证视线角速率快速、稳定收敛于0，且收敛速度优于LISMGL和BPNGL，可以更为有效地实现对目标的准确打击；与此同时，由于采用了非线性积分滑模面（（15）式），在制导过程末端，GNISMGL保证视线角能够更加准确地收敛于期望视线角qd=20°，视线角收敛时的稳态误差更小，从而保证导弹以更加接近期望攻击角的角度对目标实施拦截打击。

图3 弹目相对运动轨迹Fig.3 Curves of relative movements between missile and target

图4 视线角速率变化曲线Fig.4 Curves of light of sight angle rate

图6为考虑攻击角约束和自动驾驶仪动态特性的导弹GNISMGL、LISMGL和BPNGL 3种制导律产生的导弹法向过载指令变化曲线。如图6所示，GNISMGL有效减小了导弹末端的需用法向过载。特别是，在算例2中，当t=7 s和t=10 s时，由于目标机动性的影响，目标加速度发生突变，导弹自身的法向过载指令也会发生突变。从图6中可以看出，较之LISMGL和BPNGL，GNISMGL抑制目标机动变化的能力更强，且使导弹在面对目标机动突变时所需的法向过载更小。在制导末端，由于导引头停止工作，LISMGL和BPNGL会出现需用过载颤振或发散现象，而GNISMGL有效抑制了该现象，保证了导弹对机动目标的精确打击。同时，GNISMGL所需的法向过载平稳变化且小于LISMGL和BPNGL.因此，GNISMGL虽然在制导初期使得导弹的需用过载达到限幅，但其降低了导弹拦截末段的需用过载，提高了导弹武器的可靠性，当导弹可用过载一定时，能够使导弹有效地攻击机动性更高的目标。

图5 视线角变化曲线Fig.5 Curves of light of sight angle

图6 法向过载指令曲线Fig.6 Curves of commands of normal overload

图7为GNISMGL和LISMGL中滑模面对比曲线。所设计的全局非线性积分滑模面中由于存在非线性积分项和全局时变项Λexp（-ηt），使得制导开始时刻滑模面S=0，系统的状态就落在滑模面上，制导系统在全局过程中均具有很强的鲁棒性。此外，所设计的非线性积分项改善了滑模面收敛前的暂态性能，减小了滑模面收敛于S=0时的稳态误差，保证攻击时刻导弹的攻击角更接近所设计的期望攻击角。

图7 滑模面变化曲线Fig.7 Curves of sliding mode surface

图8给出了拦截过程中弹目相对距离的变化情况，可以看出GNISMGL能够保证导弹以更小的脱靶量命中目标，保证了导弹对目标的有效拦截。此外，为了验证考虑自动驾驶仪动态特性的GNISMGL设计的工程意义，图9给出它与传统的GNISMGL设计产生的法向过载指令对比曲线。传统的GNISMGL设计产生的法向过载指令为

式中：aMc为传统的GNISMGL设计产生法向过载指令。由图9可以看出，考虑自动驾驶仪动态特性的GNISMGL设计消除了制导回路和控制系统之间的延迟和动态特性，减小了过载指令的响应时间，降低了由于自动驾驶仪动态特性对目标机动时系统制导精度的影响。

图8 弹目相对距离变化曲线Fig.8 Curves of relative distance between missile and target

表1为两种算例下GNISMGL、LISMGL和BPNGL 3种制导律的制导参数对比情况。由表1中数据可以看出，当目标机动运动，GNISMGL能够保证导弹以更小的脱靶量和更为理想的攻击角对目标实施拦截打击，全面验证了GNISMGL的有效性和优越性。

图9 法向过载指令对比曲线Fig.9 Contrast curves of command of normal overload

表1 GNISMGL、LISMGL和BPNGL的制导仿真结果比较Tab.1 Comparison among the guidance simulation results of GNISMGL，LISMGL and BPNGL

为了进一步说明GNISMGL在拦截过程中的鲁棒性，考虑导引头对弹目相对运动相关状态量存在±2%的测量误差，假设：

同时对于算例2中的做非周期性机动的目标以5种不同的初始弹道倾角实施拦截打击（即初始弹道倾角θM（0）分别为0°、30°、60°、90°、120°，其他初始条件与制导系统参数不变，仿真结果如表2所示。

表2 不同初始条件下的GNISMGL的制导仿真结果比较Tab.2 Comparison between the guidance simulation results of GNISMGL under different initial conditions

表2为初始弹道倾角不同，导弹最终命中目标时的仿真结果。由表2可以看出，由于考虑导引头存在探测误差，当考虑自动驾驶仪的动态特性时，在不同初始条件下GNISMGL能够保证制导系统的脱靶量小于1 m，终端视线角与期望视线角之间的误差小于5°.因此，当存在导引头测量偏差时，采用不同的初始发射角（弹道倾角）均能保证导弹在满足所需攻击角的情况下对非周期性机动目标的精确打击。图10形象地表示了不同情况下拦截过程中弹目相对运动轨迹，从而表明了所设计的GNISMGL对测量误差和不同初始条件具有强鲁棒性。

图10 不同初始条件下的弹目运动轨迹Fig.3 Curves of engaged movements between missile and target under different initial conditions

图11和图12为不同初始条件下弹目视线角和视线角速率的变化曲线。由图11和图12可以看出，在不同初始条件下，当考虑导引头测量偏差时，导弹在拦截过程中均能保证视线角有效收敛于期望视线角qd=20°，视线角速率收敛于0.由于存在如（68）式所示的测量误差，在GNISMGL作用下，视线角和视线角速率并未出现明显的发散，只是出现了在期望值附近呈正弦形式的上下波动。因此，说明了在制导系统对期望值的跟踪过程中，GNISMGL对外界扰动具有很强的抑制作用。

图11 不同初始条件下视线角变化曲线Fig.11 Curves of light of sight angle under different initial conditions

图12 不同初始条件下视线角速率变化曲线Fig.12 Curves of light of sight angle rate under different initial conditions

如图13所示，所设计的全局非线性积分滑模面中由于全局时变项Λexp（-ηt），尽管仿真开始时初始条件不同，但仍保证制导开始时刻滑模面S=0，从而使得制导系统在全局过程中均具有很强的鲁棒性。同时，从图13可以看出，虽然仿真过程中存在测量精度上的干扰，继而引起对状态量测量存在摄动，但所设计的全局非线性积分滑模面在保证很小稳态误差的前提下，最终均能收敛于0，很大程度上说明了所设计的GNISMGL是一种对于已知或未知的系统不确定性具有很好鲁棒性和稳定性的制导律。图14和图15分别表示了在不同初始条件下拦截过程中弹目相对距离的变化情况和导弹需用法向过载的变化情况。仿真结果表明，GNISMGL能够保证导弹在需用法向过载限制范围内即便以不同的初始发射条件，均能保证对目标的精确打击。

图13 不同初始条件下滑模面变化曲线Fig.13 Curves of sliding mode surface under different initial conditions

图14 不同初始条件下弹目相对距离变化曲线Fig.14 Curves of relative distance between missile and target under different initial conditions

图15 不同初始条件下导弹法向过载变化曲线Fig.15 Curves of normal overload of missile under different initial conditions

5 结论

针对导弹拦截机动目标的问题，考虑攻击角约束和自动驾驶仪动态特性，结合积分滑模和全局滑模的控制方法，设计了一种全新的非线性积分滑模制导律，并与传统积分滑模制导律和BPNGL进行对比。仿真结果说明了所设计的GNISMGL能够对机动目标实现精确拦截打击，同时有效改善了制导系统的暂态性能，使系统在整个制导过程中均具有很强的鲁棒性，减小了滑模面收敛时的稳态误差，保证导弹能够在制导末端具有更为理想的攻击角。同时针对不同初始条件下的机动目标拦截问题，全面验证了GNISMGL的有效性和优越性。

（

）

［1］Zhang Y A，Ma G X，Liu A L.Guidance law with impact time and impact angle constraints［J］.Chinese Journal of Aeronautics，2013，26（4）：960-966.

［2］Byung S K，Jang G L H，Hyung S H.Biased PNG law for impactwith angular constraint［J］.IEEE Transactions on Aerospace and Electronic Systems，1998，34（1）：277-288.

［3］Lu P，Doman D B，Schierman J D.Adaptive terminal guidance for hypervelocity impact in specified direction［J］.Journal of Guidance，Control，and Dynamics.2006，29（2）：269-278.

［4］Manchester I R，Savkin A K.Circular-navigation-guidance law for precision missile/target engagements［J］.Journal of Guidance，Control，and Dynamics，2006，29（2）：314-320.

［5］胡锡精，黄雪梅.具有碰撞角约束的三维圆轨迹制导律［J］.航空学报，2012，33（3）：508-519. HU Xi-jing，HUANG Xue-mei.Three-dimensional circular guidance law with impact angle constraints［J］.Acta Aeronautica et Astronautica Sinica，2012，33（3）：508-519.（in Chinese）

［6］Kim M，Grider K V.Terminal guidance for impact attitude angle constrainted flight trajectories［J］.IEEE Transactions on Aerospace and Electronic Systems，1973，9（5）：852-859.

［7］Idan M，Golan O M，Guelman M.Optimal planar interception with terminal constraint［J］.Journal of Guidance，Control，and Dynamics，1995，18（6）：1078-1083.

［8］Song T L，Shin S J.Time-optimal impact angle control for vertical plane engagements［J］.IEEE Transactions on Aerospace and E-lectronic Systems，1999，35（2）：738-742.

［9］Song T L，Shin C D，Cho H.Impact angle control for planar engagements［J］.IEEE Transactions on Aerospace and Electronic Systems，1999，35（4）：1439-1444.

［10］Ohlmeyer E J，Phillips C A.Generalized vector explicit guidance［J］.Journal of Guidance，Control，and Dynamics，2006，29（2）：261-268.

［11］Zhang Q Z，Wang Z B，Tao F.Optimal guidance law design for impact with terminal angle of attack constraint［J］.Optik，2014，125（1）：243-251.

［12］Shaferman V，Shima T.Linear quadratic guidance laws for imposing a terminal intercept angle［J］.Journal of Guidance，Control，and Dynamics，2008，31（5）：1400-1412.

［13］Sachit R，Debasish G.Terminal impact angle constrained guidance laws using variable structure systems theory［J］.IEEE Transactions on Control Systems Technology，2013，21（6）：2350-2359.

［14］Lee C H，Kim T H，Tahk M J.Design of impact angle control guidance laws via high-performance sliding mode control［J］. Proceedings of the Institution of Mechanical Engineers，Part G：Journal of Aerospace Engineering，2012，227（2）：235-253.

［15］窦荣斌，张科.基于二阶滑模的再入飞行器末制导律研究［J］.宇航学报，2011，32（10）：2109-2114. DOU Rong-bin，ZHANG Ke.Research on terminal guidance law for re-entry vehicle based on second-order sliding mode control［J］. Journal of Astronautics，2011，32（10）：2109-2114.（in Chinese）

［16］熊俊辉，唐胜景，郭杰，等.基于模糊变系数策略的迎击拦截变结构制导律设计［J］.兵工学报，2014，35（1）：134-139. XIONG Jun-hui，TANG Sheng-jing，GUO Jie，et al.Design of variable structure guidance law for head-on interception based on variable coefficient strategy［J］.Acta Armamentarii，2014，35（1）：134-139.（in Chinese）

［17］李鹏.传统和高阶滑模控制研究及其应用［D］.湖南：国防科学技术大学，2011. LI Peng.Research and application of traditional and higher-order sliding mode control［D］.Hunan：National University of Defense Technology，2011.（in Chinese）

［18］Liu J K，He Y Z.Fuzzy global sliding mode control based on genetic algorithm and its application for flight simulator servo system［J］. Chinese Journal of Mechanical Engineering，2007，20（3）：13-17.

［19］Chen R H，Speyer J L，Lianos D.Optimal intercept missile guidance strategies with autopilot［J］.Journal of Guidance，Control，and Dynamics，2010，33（4）：1264-1272.

［20］Zhang Z X，Li S H，Luo S.Composite guidance laws based on sliding mode control with impact angle constraint and autopilot lag［J］.Transactions of the Institute of Measurement and Control，2013，35（6）：764-776.

［21］刁兆师，单家元.考虑自动驾驶仪动态特性的含攻击角约束的反演递推制导律［J］.宇航学报，2014，35（7）：818-826. DIAO Zhao-shi，SHAN Jia-yuan.Back-stepping guidance law with autopilot lag for attack angle constrained trajectories［J］. Journal of Astronautics，2014，35（7）：818-826.（in Chinese）

［22］曲萍萍，周荻.考虑导弹自动驾驶仪二阶动态特性的三维制导律［J］.航空学报，2011，32（11）：2096-2105. QU Ping-ping，ZHOU Di.Three dimensional guidance law accounting for second-order dynamics of missile autopilot［J］.Acta Aeronautica of Astronautica Sinica，2011，32（11）：2096-2105.（in Chinese）

［23］Zhou D，Qu P P，Sun S.A guidance law with terminal impact angle constraint accounting for missile autopilot［J］.Journal of Dynamic Systems，Measurement，and Control，2013，135（5）：1-10.

［24］Hou M Z，Liang X L，Duan G R.Adaptive block dynamic surface control for integrated missile guidance and autopilot［J］. Chinese Journal of Aeronautics，2013，26（3）：741-750.

［25］Bhat S P，Bernstein D S.Finite-time stability of homogeneous systems［C］∥Proceedings of American Control Conference.Albuquerque，New Mexico，US：IEEE，1997：2513-2514.

［26］Khalil H.Nonlinear systems［M］.New Jersey，US：Prentice Hall，1996：83-87.

［27］Zhang Z X，Li S H，Luo S.Terminal guidance laws of missile based on ISMC and NDOB with impact angle constraint［J］.Aerospace Science and Technology，2013，31（1）：30-41.

A Novel Sliding Mode Guidance Law with Impact Angle Constraint for Maneuvering Target Interception

ZHANG Yao，GUO Jie，TANG Sheng-jing，SHANG Wei，ZHANG Hao-qiang
（Key Laboratory of Dynamics and Control of Flight Vehicle of Ministry of Education，School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China）

A novel missile sliding mode guidance law（SMGL）in which a missile intercepts maneuvering target is proposed，which is based on a combination of the advantages of integral sliding mode control and global sliding mode control.The relative motion equations of missile and target，in which the impact angle constraints are considered，are established within the perpendicular plane.A new nonlinear saturation function is adopted to construct an integral term in global integral sliding mode surface，and then an improved nonlinear global integral sliding mode control technique is presented，which solves the problem about system transient performance deterioration and decreases the steady state errors.It is obvious that the designed guidance law enables the missile to hit target at a desirable impact angle in finite time，and the missile to be of strong robustness during the whole interception.The missile global nonlinear integral SMGL in which the autopilot dynamics and impact angle constraints are considered is investigated by adopting dynamic surface control.It is demonstrated that all states in the closed loop system are ultimatelybounded on the account of Lyapunov stability theorem.The simulation results verify the effectiveness and superiority of global nonlinear integral SMGL.

control and navigation technology of aircraft；guidance law；global nonlinear integral sliding mode；dynamic surface control；impact angle constraint

TN765.1

A

1000-1093（2015）08-1443-15

10.3969/j.issn.1000-1093.2015.08.011

2014-10-10

国家自然科学基金项目（11202024）；航空科学基金项目（2012ZA720002）

张尧（1991—），男，博士研究生。E-mail：bit_fsdzhangyao@sina.com；郭杰（1981—），男，讲师。E-mail：guojie1981@bit.edu.cn；唐胜景（1959—），男，教授，博士生导师。E-mail：tangsj@bit.edu.cn