现代物流装卸单元的技术优化策略及模型分析

王静

西北政法大学商学院，陕西西安710063

现代物流装卸单元的技术优化策略及模型分析

王静

西北政法大学商学院，陕西西安710063

为了提高货物的流通速度，提高物流设施、设备空间的利用率，以装卸单元为研究对象，基于码放策略分析，运用装卸单元最少化方法，设计并建立物流装卸单元体积优化的数学规划模型。研究结果表明：码放策略是为了优化装卸单元的堆码空间，使单元的填充能力达到最大；装卸单元最少化是一种能满足一定的约束条件，将订单所需要的货物填充到最少的装卸单元中去的一种方法；针对模型特殊结构，提供了基于体积优化的装卸单元模型可使体积的利用率最大的建模方法。通过实例仿真验证，该方法具有较好的可行性和实用性。能达到物流单元的标准化和合理化，使包装尺寸和集装单元的尺寸符合一定的标准。

物流装卸单元；码放策略；体积优化；数学规划模型

装卸单元的优化对物流单元的标准化和合理化至关重要。合理组织装卸能够降低物流成本，提高配送效率。为使包装尺寸和集装单元的尺寸符合一定的标准，首先应确定码放策略。码放的优化是一个多维混合优化问题［1，2］。在运筹学中，采用的是体积比较的方法，即对给定的填充单元和装卸单元，找出所有可能的排列组合方式。进而根据填充约束条件，比较填充度，找出码放最优的模式［3，4］。这种方法对解决填充单元大小不同的问题，还有一定的难度。由于装卸单元中填充什么单元或填充多少，不应是对码放优化的问题。因此本文提出在物流操作中，按给定的填充任务完成装卸单元的填充工作的码放策略，研究将订单所需要的货物填充到最少的装卸单元中去的方法，在此基础上建立了物流装卸单元体积优化的数学规划模型，并给出了填充度ŋpack与经验系数fstr的关系求解，从而达到物流单元优化的目的。本文将探讨用数学规划方法求解物流装卸单元的优化问题。

1 码放策略分析

1.1 同种规格的填充单元的平行码放策略

将填充单元放在荷重载体的一角，使填充体的每一个面按预先给定的方向与装卸单元的里表面平行，无缝隙地一个挨一个，使各层码放方式相同，上下对应。

如果填充单元的长边l与装卸单元的长边L对齐，宽边b与装卸单元的宽边B对齐，高度h与装卸单元的高度H对齐，则装卸单元的填充能力为：

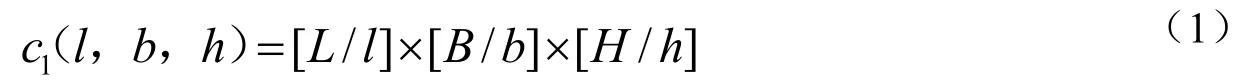
如果存在高度方向约束，码放方案可通过调整长、宽方向的对应关系，比较装卸单元的填充能力得到：此时，最优码放策略就是两种方案中装卸单元的填充能力最大的一种。此时，装卸单元的填充能力C2A为：

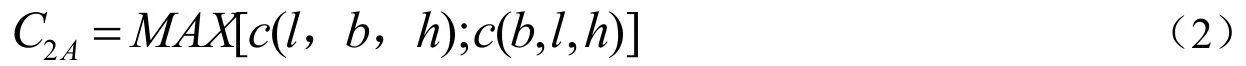
如果存在摆放约束，最优的码放策略应首先选择填充单元的标签粘贴面，使装卸单元的填充能力最大。此时填充单元的摆放模式即为最优码放模式。此时，装卸单元的填充能力C2B为

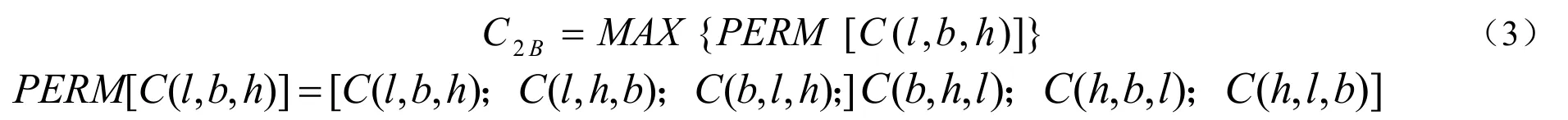
在装卸单元与填充单元的尺寸不匹配时，根据平行码放策略，按不同长度方向码放填充单元时的剩余长度。很显然，在装卸单元和/或填充单元的尺寸可调时，剩余长度是可避免的。由此，产生了第二种码放策略。

1.2 剩余空间利用策略

如果装卸单元的内空尺寸和填充单元的外部尺寸存在下列整数关系。

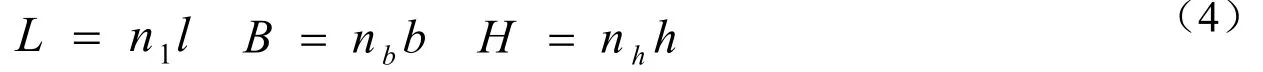
则由尺寸适配的优化策略，装卸单元的填充能力C为：

采用这种方式可使单元的填充度ηpack=100%。

如果装卸单元的内空尺寸和填充单元的外部尺寸之间不存在整数关系，可通过下列方法进行调整。

（1）在剩余空间，保持高度对应关系不变的平行码放策略

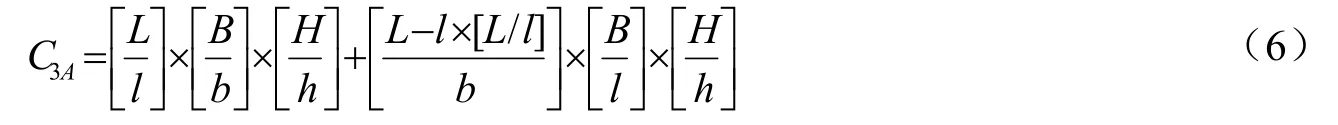
（2）在剩余空间，高度对应关系可变的平行码放策略第一步：如果剩余长度，可在长度方向继续堆码。将填充单元的长和宽的对应关系或宽与长的对应关系交换。

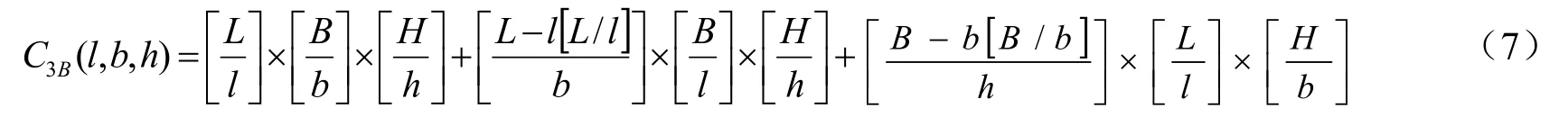
将平行码放策略，剩余空间利用与高度方向约束及摆放约束结合所得到的策略称为码放策略4A；将平行码放策略，剩余空间利用摆放约束结合所得到的策略，称为码放策略4B。则采用这两种策略时，装卸单元的填充能力计算就需将式（3）中的用式（6）的C3A或式（7）的C3B代替。

1.3 不同填充策略的填充度比较

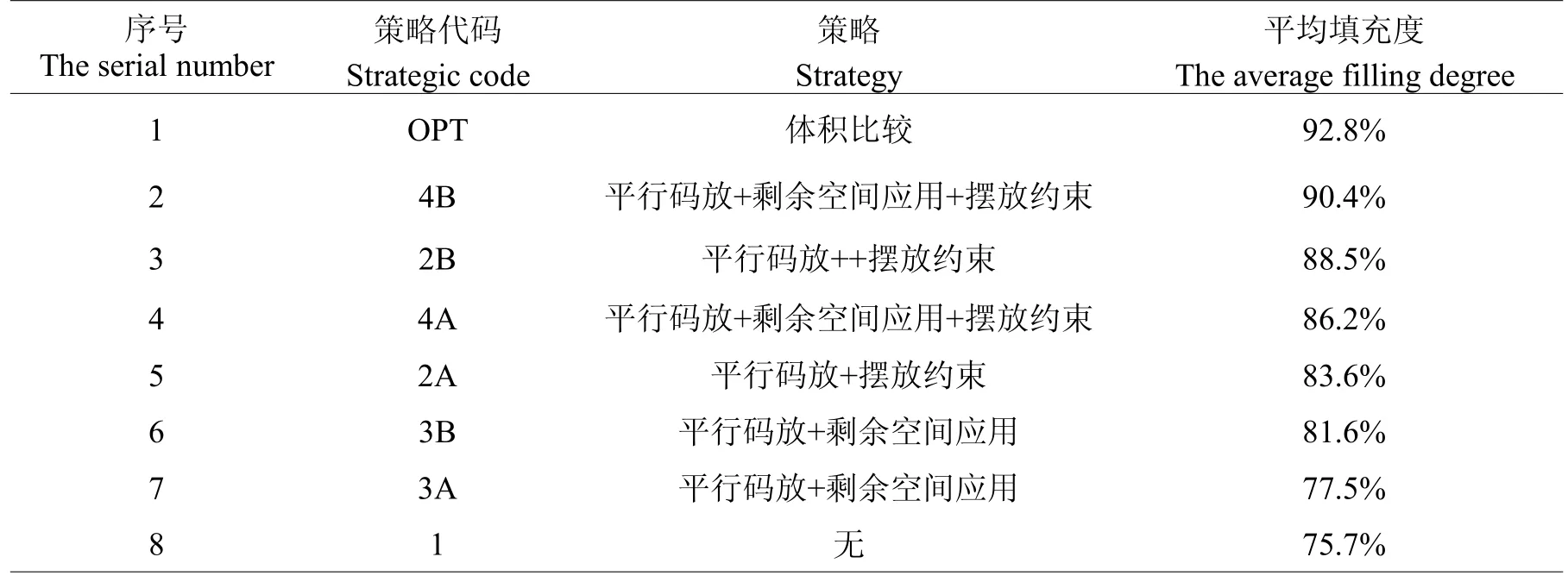
表1 不同的码放策略的填充度比较Table 1 Filling degree of comparison of different strategy pattern

表1给出了由50个不同的填充任务，按不同的码放策略在托盘上码放时的填充度。其中每个立方体填充单元的平均体积为18 L，填充单元的l：b=1.46，托盘的填充空间为1323 L。

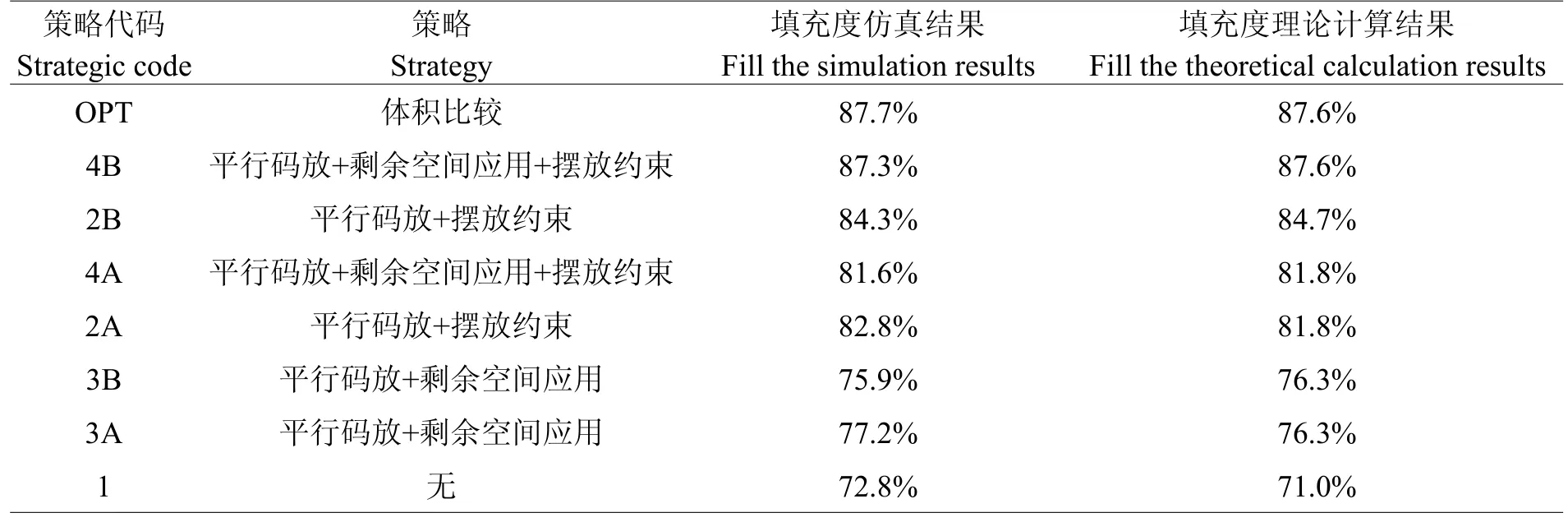
表2 不同码放策略的填充度仿真结果比较Table 2 Different strategy pattern of filling degree of the simulation results

表2表示了用50个立方体填充单元在托盘上码放时的填充度随机仿真结果，托盘的填充空间是填充单元平均体积的100倍。填充单元的l：b=1.46，b：h=2.2。

由表1和表2出发，不断变化体积比VLE/υFE、装卸单元的内空尺寸和有向外朝向要求的面，继续仿真计算，可得如下结论：

（1）随着体积比VLE/υFE的增加，不同码放策略的填充度都会不同程度地减小；

（2）当体积比VLE/υFE≥100时，即填充单元的尺寸小于装卸单元内空尺寸的1/5时，按码放策略4B所得的平均填充度与按体积比较优化所得结果相差不到0.5%；

（3）当体积比VLE/υFE＜10时，即填充单元的尺寸大于装卸单元内空尺寸的1/3时，按体积比较优化的平均填充度与按码放策略4B所得的结果高出10%；

（4）按码放策略2B和码放策略3B进行码放，所得的平均填充度基本一致；

（5）当体积比VLE/υFE≥100时，按码放策略2B和码放策略3B进行码放，所得的平均填充度比体积比较优化所得结果小5%；

（6）当体积比VLE/υFE＜10时，按码放策略2B和码放策略3B进行码放，所得的平均填充度比体积比较优化所得结果小10%。

2 装卸单元最少化方法

2.1 装卸单元最少化的约束条件

经常性的约束条件有如下几项。

2.1.1 目的地约束一个装卸单元只能装载送达同一目的地的货物。如果一个填充任务要将一些货物发往多个目的地，目的地的顺序与订单顺序一致，可按订单顺序分别填充货物［5］。此时多种货物混装是允许的。

如果填充货物的目的地顺序与装卸单元中的送货单元顺序一致，送达一个目的地的送货单元不能和送达其他地方的送货单元混装在一个装卸单元中。此时，装卸单元中的订单可有多个，且货物可有多种。考虑顺序约束时，意味着装车的顺序应与到达的目的地的顺序相反，避免重复装卸；在仓库中意味着货物的先进先出。

2.1.2 许用承载能力约束即要求不超过填充单元的承压能力和装卸单元的许用荷重。为此，填充时应首先码放重的、大的和承压能力较大的填充单元，在往上填充轻的、小的和承压能力较小的填充单元。

式中，mFA为每个任务的填充量；G为装卸单元的净重；g为填充单元的平均质量。

2.1.3 填充能力与填充量的配合约束即每个任务的填充量mFA应是装卸单元的填充能力CLE和所需装卸单元个数MFA的整数倍，通过填充量配合的策略防止截断损失［6］。比如在生产过程中，生产量应是托盘装填能力的整数倍；补货时，每次托盘上的补货量或库存量应能保证托盘能力得到充分发挥；运输时，运输工具的能力应得到充分满足。

对于填充任务而言，填充能力的配合策略意味着通过选择填充的荷重载体使装卸单元的填充能力得到充分发挥。对于托盘的填充任务就存在不同规格的托盘和不同大小的托盘填充高度，使托盘的填充能力得到充分发挥。对于运输工具的选择，就应根据装卸单元的大小，使运输工具的填充能力得到充分发挥［7］。

在装卸单元的填充能力满足时，所需的装卸单元的个数应为整数MFA。

很显然，填充能力的配合策略并不能完全防止截断损失，但能改善装卸单元的填充度。若要进一步改善填充度，可将填充量配合的策略和填充能力的配合策略结合起来。

2.2 装卸单元数量的优化

海运、空运和汽车运输的货物都是处于混合状态，其运量可用填充货物的总质量mA或填充货物的总体积mB表示。

如果装卸单元的质量为GLE，体积为VLE，则装卸单元的质量体积比。

如果填充单元的平均体积为υA，平均质量为gA，当填充单元的平均质量体积比时，则由质量定义的装卸单元（A类单元）填充能力为

如果填充单元的平均体积为υB，平均质量为个gB，当填充单元的质量体积比γB=gB/υB＜γLE时，对于某一填充度ηpack，由体积定义的装卸单元（B类单元）填充能力为：

当运输工具按质量和体积分区装货时，所需要的装卸单元总数

其中由mA/CA确定的填充单元只满足了装卸单元承载能力的要求，而空间没有充分运用；由mB/CB所确定的填充单元只满足了装卸单元空间利用的要求，而承载能力没有充分运用［8］。

如果装卸单元按质量、体积混装时，由质量定义的填充单元的最优数CAopt和满足一定填充比的、由体积定义的填充单元的最优数CBopt，存在如下关系。

解此方程组，可得混装单元的填充单元的分配数为：

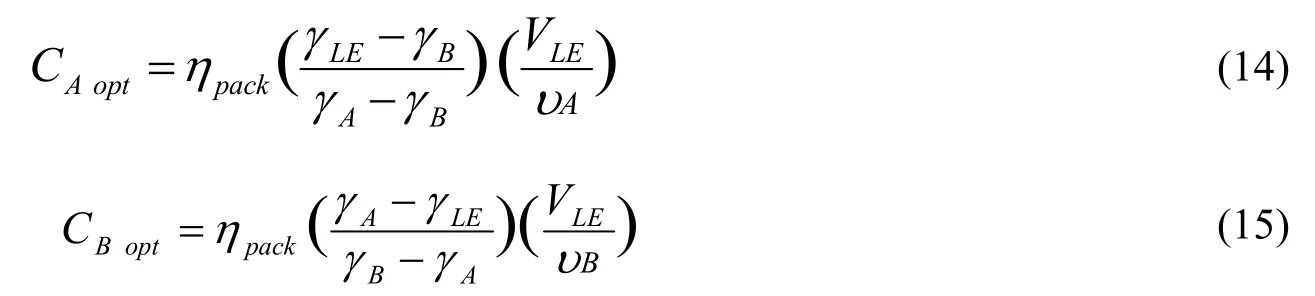
如果存在关系：γA＞γLE＞Bγ，按下列方法，可得由每个装卸单元的装填最优数CAop和CBop，确定每种装卸单元的个数。

第一步：按最优数CAopt和CBopt填充装卸单元，直到由运输任务mA和mB所确定的所有的填充单元全部装完。所需的混装装卸单元个数MAB为：

第二步：如果装填混装单元后，（mA—MABCAopt）＞0，需要补充A类装卸单元

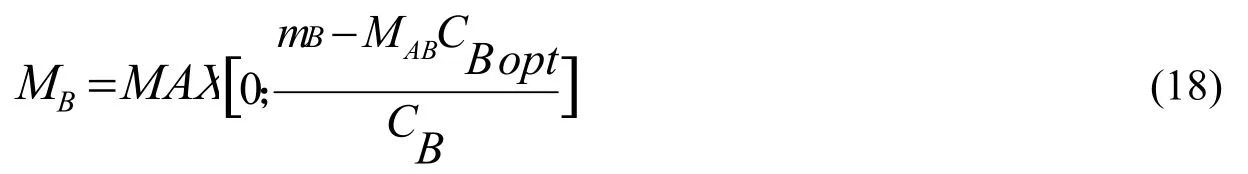
则所需要的不同种类的装卸单元数的总和的最小值Mopt为：

且γA＞γLE＞Bγ，通过装卸单元数量优化，可减少所需要的装卸单元数20%。

3 物流装卸单元体积优化的数学规划模型

装卸单元的体积利用率Vη是每个任务的填充量mFA与填充单元的体积υFE的乘积和MFA个装卸单元的总容积之比，即

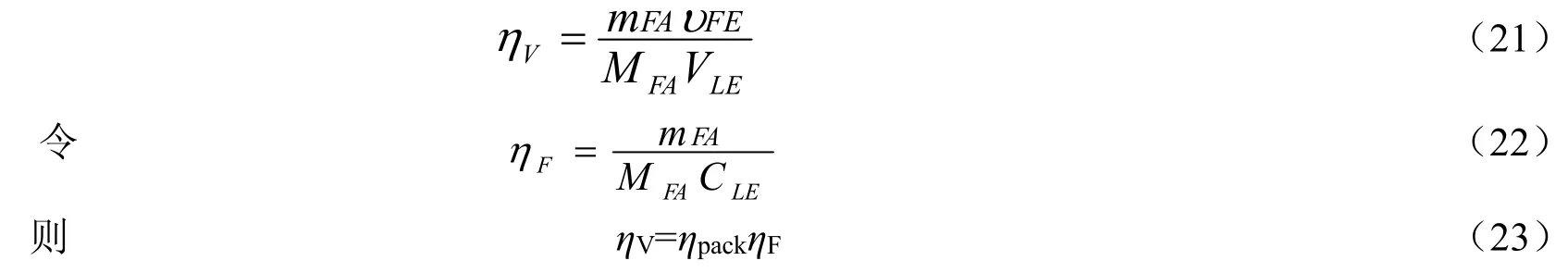
填充度ηpack与码放策略有关，通过理论分析和计算机仿真，ηpack与经验系数fstr的关系可用下式表示［9］。

其中经验系数fstr的数值与码放策略的对应关系见表3。

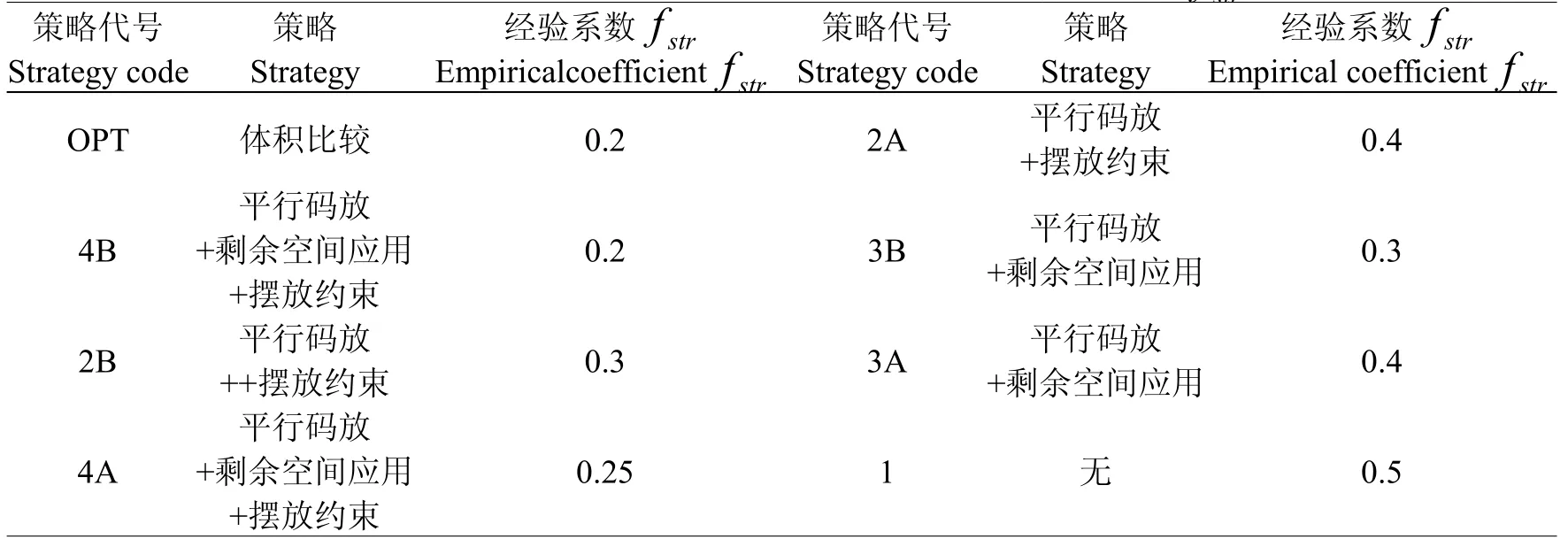
表3 各种码放策略的经验系数fstrTable 3 The experience coefficient of various strategy patternfstr

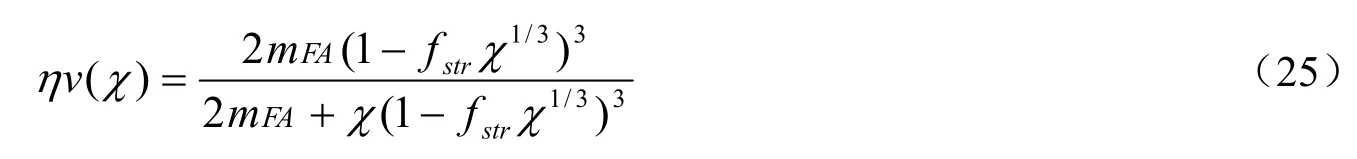
在mFA=800，经验系数fstr=0.5时，体积利用率ηV与相对填充体积χ的关系见图1。最优的装卸单元的体积VLE=200 υFE，最优的体积利用率ηV=70%。

对式（25）求导，并令导数为零，可得

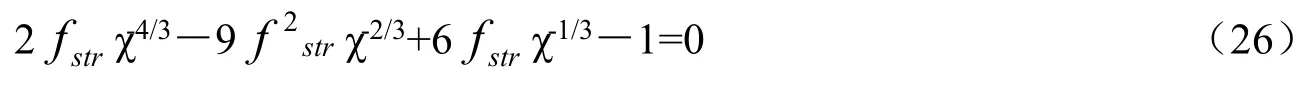
式（26）的求解可通过设定经验系数fstr求解。图2表示了fstr=0.30和fstr=0.20两种情况下，最优的相对填充体积χopt与填充单元数mFA的关系。

大多数情况，最优相对填充体积χopt的求解可通过下列近似公式进行计算。

因此，在不考虑填充能力与填充量的配合性约束时，装卸单元的最优体积应为

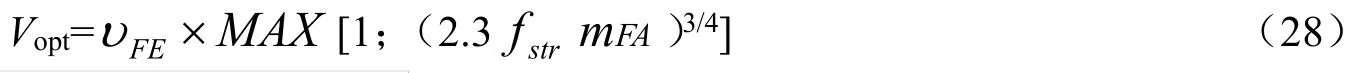
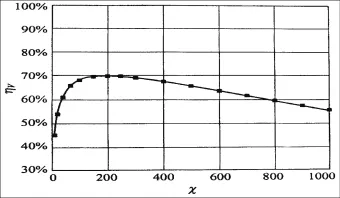
图1 体积利用率vη与相对填充体积χ的关系Fig.1Volumeutilizationratiovηandtherelativevolume filledχrelationship

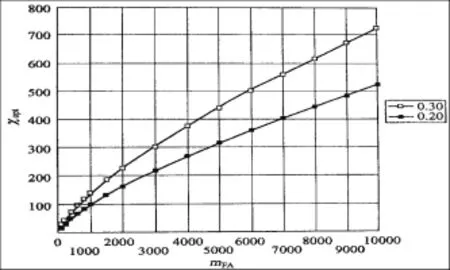
图2 最优相对填充体积χopt与填充单元数mFA的关系Fig.2Theoptimalrelativefillingvolumeχoptandfillingunit numbermFArelationship

4 实例仿真

这里以某物流中心的装卸单元为例，进行了上述体积优化的装卸单元模型的仿真与验证。装卸单元的质量体积G0=40。货物分4类8件，第一类货物有3种，G11=6，G12=9，G13=5；第二类货物有2种，G21=8，G22=9；第三类货物有1种，G31=15；第四类货物有2种，G41=16，G42=20。

寻求最优解的次序与计算过程如表4～7所示［10］：

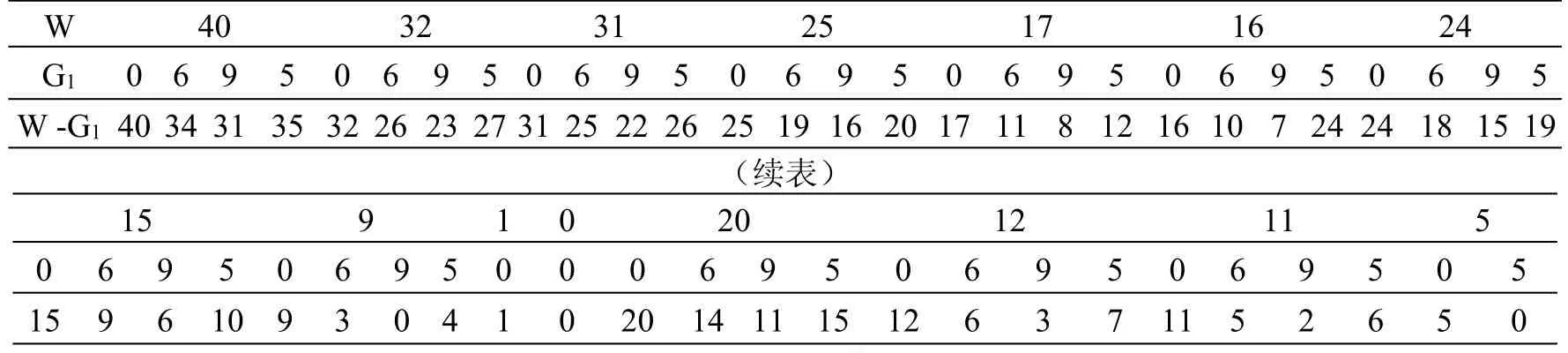
表4 第一阶段计算表Table 4 The first phase calculation table

表5 第二阶段计算表Table 5 The second phase calculation table

表6 第三阶段计算表Table 6 The third phase calculation table

表7 第四阶段计算表Table 7 The fourth phase calculation table

所求各组最优解，每组装卸单元的质量体积都是40，达到最优的体积利用率，充分利用了物流的装卸能力。

5 结语

（1）码放策略分析是为了优化装卸单元的堆码空间，使单元的填充能力达到最大。装卸单元最少化为了减小填充任务的截断损失，将填充任务所需要的装卸单元数最少化。

（2）装卸单元最少化方法是一种能满足一定的约束条件，将订单所需要的货物填充到最少的装卸单元中去的一种方法。

（3）通过以上研究，建立了物流装卸单元体积优化的数学规划模型。物流成本随装卸单元的数量、体积和总重的增加而增加，装卸单元的数量则随装载体积的增加而减小，基于成本优化的装卸单元的问题，即对于给定的填充任务或订单系列，寻求体积优化的装卸单元。基于体积优化的装卸单元模型可使体积的利用率最大。

（4）针对模型特殊结构，提供了切实可行的建模方法。通过实例仿真验证，该方法具有较好的可行性和实用性。能达到物流单元的标准化和合理化，使包装尺寸和集装单元的尺寸符合一定的标准。

［1］Holger Luczak.Logistik-Benchmarking［M］.Heiderberg：Springer.2004：128-133

［2］Domschke Drexl.Logistik：Standorte［M］.Muechen：Oldenbourg.1996：148-156

［3］张莹.运筹学基础［M］.北京：清华大学出版社，1995：205-214

［4］赵刚.物流运筹［M］.四川：四川人民出版社，2002：156-163

［5］张晓川.现代仓储物流技术与装备［M］.北京：化学工业出版社，2003：189-195

［6］Wu H J，Dunn S.Environmentally Responsible Logistics Systems［J］.International Journal of Physical Distribution and Logistics Management，1995，25（2）：20-23

［7］方仲民.物流系统规划与设计［M］.北京：机械工业出版社，2003：122-131

［8］朱伟生.物流成本管理［M］.北京：机械工业出版社，2003：222-227

［9］蔡临宁.物流系统规划——建模及实例分析［M］.北京：机械工业出版社，2003：186

［10］秦明森.物流作业优化方法［M］.北京：中国物资出版社，2003：103-106

Modern Logistics Technology Optimization Strategy and Model Analysis of Loading and Unloading Unit

WANG Jing
Northwest University of Political Science and Law School，Xi'an 710063，China

In order to improve the velocity of circulation of goods，improve the utilization rate of logistics facilities，equipment，space，loading and unloading unit as the research object，based on strategy analysis pattern，and using the methods of handling unit at least，to design and establish the logistics handling unit volume optimization mathematical programming model.The research results show that the strategy pattern is to optimize the loading/unloading unit of stack space，maximize the filling ability of the unit；Handling unit minimization is a kind of can satisfy certain constraint conditions，the order will be the goods need to fill into the least handling unit of a method；In view of the special structure model，provides a handling unit models based on volume optimization modeling method can make the utilization rate of the volume of the largest.Through example simulation validation，the method has better feasibility and practicability.To achieve standardization and rationalization of logistics units，make the packing size and the size of container is in accordance with certain standards.

Logistics handling unit；strategy pattern；volume optimization；mathematical programming model

F127

A

1000-2324（2015）01-0121-07

2013-02-13

2013-04-22

中国博士后科学基金第五十四批面上资助项目（2013M541552）；2013年度陕西省社科基金资助研究项目（13D085）；中国建筑第八工程局有限公司科技研发项目（2012-28）；中铁十四局常电扩建工程项目（2014-3）；西安市科学技术局产业技术创新计划项目（CXY1429（1））

王静（1970-），女，陕西西安人，副教授，硕士生导师，马克思主义理论博士后，管理科学与工程博士后，主要从事中国特色社会主义理论与实践、物流工程与管理研究.E-mai：wjing818@126.com