马克思·比尔数模思维中的设计原理
王彤蕾
(安徽师范大学 美术学院,安徽 芜湖 241000)
马克思·比尔数模思维中的设计原理
王彤蕾
(安徽师范大学美术学院,安徽芜湖241000)
任何一种设计的诞生都是由于物理缺陷和心理缺陷导致的,人类为了弥补缺陷而想出的设计.舍勒认为“人类既然缺乏专门化的器官和本能,自然就不能适应他自身的特殊环境.”本文将从马克思·比尔的数模思维的海报设计.
设计;目的因;本质特征;设计资源;方法论;设计原理;数模思维
1 设计原理的概述
设计的原理是把艺术的形式结合于社会各行业表现出来.艺术设计包括服装、环境、平面、工业等.把材料转换为产品.设计原理就是为了告诉人们设计的产生分析以及设计的目的因和设计的限制和设计的资源.原理就是探究这些问题并总结出来的方法论.
设计的目的因有三个方面:第一个是设计的功能性.苏格拉底曾经说过“凡是我们用的东西如果被认为是美的和善的那就都是从同一观点-它们的功用去看的.那么,篓筐能说是美的吗?当然,一面金盾却是丑的,如果篓筐适用而金盾不适用.苏格拉底的这段话就是说一个设计的东西美和善的标准就是它的功能性.如果一个设计的东西没有功能,也不能称为美的东西.适合性法则不折不扣地主宰着功能和功能美的实现,如果设计的东西仅仅只停留在美没有功能的作用,设计也不能称为一个好的设计.但是没有功能的也未必没有用.随着时代的发展,可能功能性和美观性在一个设计产品中并不都是同时存在的,越来越多的产品只是注重自己的思维表达也不太注重功能性.例如米兰的时装周里的一些衣服的设计,不仅仅考虑功能,有很多衣服是不能穿出去的,只能体现设计师的设计思维,也就是说没有功能的未必没有用的.还记得我在十月中旬的文博会,我看到用藤条做的衣服和裙子,所以说现代的设计不是说有功能就一定没用,藤条做的衣裙虽然在功能上欠缺实用,但是设计思维还是很新颖的.我们知道没有功能的东西并非无用.物的“用”是一个复杂的范畴,它不仅仅是对人的生理需求的满足,对心理的需求也仍然要满足,所以对于设计的目的我们不能仅仅只停留在功能方面,而要深入到人类心理行为研究.通过对所见的现代设计而言,功能不仅仅是设计的主要目的.第二个是设计的易用性,设计的易用性通俗来说这个设计作品好用或不好用,这是设计原理最重要的一方面,解决的是物与人类的产品效能的关系.“易用性”包含的范围有四个方面.首先有效性我认为是一个设计能为大众达到的预期效果;其次易学性应该指的是一个设计产品能够有的难度范围,并且为大众提供服务支持和帮助;再次是适应性,适应性应该指的是不同的人对产品的不同适应能力;最后指的是使用态度,是指产品设计对受众的影响及受众对产品的态度.设计的创造性特征.创造性是设计的本质属性,设计思维本身就具有创造性特征.生活和艺术之间没有籓篱,方法和规范之间也没有规限.用通俗的话来说“设计来源于生活,往往高于生活”.设计只有通过丰富的创造才会使设计的思维更加开拓.
对设计资源的整合施加不同的意识与态度,会产生资源意义不同程度的改造,对于设计而言,资源的整合再加上自己的想法意识就能成为好的作品.
2 具体艺术的发生背景及马克思·比尔的生平简介
2.1具体艺术的发生背景
马克思·比尔的数模设计引入到具体艺术中是一种将感性思维转换为理性思维.具体艺术指的是用具体的点、线、面来表现的海报艺术形式.去表达他们的艺术风格,其实具体艺术是抽象艺术的一种.具体艺术以色彩、空间、光感、和运动等作为艺术表现形式,以数学的规律性作为一种法则,并以新的法则运用在设计中.这种形式法则会带来设计的秩序美.马克思·比尔将几何形的构造引入到设计中,将数学的秩序美来表现海报的设计感.具体艺术消除所有自然现象,将绘画的具体元素点、线、面来进行数学规律的再设计从而创造出抽象性的构成简单、和谐的艺术作品.他认为具体艺术是“努力用可感觉和可触动的形式再现抽象的思想.有意识或无意识的存在,绘画或雕塑都与数模思维有密切联系,他坚持将康定斯基和马列维奇的艺术精神作为自己创作的依据.他认为数学规律就一定要用在艺术创作原则中.在他创作具体艺术的时候,向大家极致地表现出点、线、面的各个元素共存在海报设计艺术当中.
2.2比尔的生平简介
马克思·比尔(MaxBill,1908-1994)是具体艺术的杰出代表.1908年12月出生瑞士的一个小乡村,1924-1927年在苏黎世工艺美术学校学习.1927-1929年当过银匠学徒,学习过房屋建筑.1929迁居苏黎世,从事建筑、绘画、版画、和雕塑活动.1944年在贝士举办首个具体艺术国际展览.1950-1976年担任过院长,国会议员及环境设计专业的教授.1994年12月去世,享年86岁.
3 马克思·比尔的作品分析
比尔运用的设计手法是将数学内在规律与平面设计相结合的手法,并极致地展现出点、线、面在平面设计中所体现的艺术特点.在他众多作品中,能够很清楚地看出作者的思维轨迹在艺术中的运用.同一主题下的变异作品是马克思·比尔的典型作品.我们能够从作品中看到“数模思维”是如何表现在设计作品中的.
3.1关于主题
中心是由一个没有合起来的等边三角形向外延展.第三边向外展开,并继续以线条不断向外延伸.线条连接三角形的第三条边向外形成一个向外延展的正方形,以同样方式形成一个正五边形、正六边形、正七边形,并最终形成一个等边八边形.我们可以看到,从等边三角形开始的一条边被打开后作为第一个正多边形结束,又组成另外一个正多边形的开始,这一条边又开始无限伸展,规律中又带着变化,看似有规律但其实有无限地伸展力,形成看似完成而又未完成的变化的意味.
3.2“点”的运用
这个点的海报设计是十分的巧妙.每个正多边形的顶点以小色点的形式表现出来,并去除连接线,以单独色点为独立部分,而双色点就是多边形相连接的部分,色点的规律是依照主题的规律而言,无限延展的而无封闭的线条,使得这幅作品即是运动而又在变化之中的.

3.3“线”的运用
这张图形是由主题图形构成.等边三角形的一边是圆的直径,并依此延展.每个正多边形的闭合部分都是半圆.每两个为直径的圆形都是正多边形的闭合部分为间隔.圆形是由正多边形的线展开而多为直径的圆形构成,这幅作品是由多边形和为直径的圆形构成.
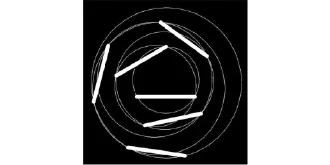
通过对这张图的分析,这张设计作品是由大大小小的圆形构成的.第一个圆形是以等边三角形的三个点为基础,第二个圆形是由正四边形的四个顶点为基础的,以此类推第三个圆形是由正五边形的五个顶点为寄出的,至到第四个,第五个………由圆形和线段组成的螺旋图形.马克思?比尔的设计作品必须要用数学的几何思维来进行作品分析,他的作品看似具体,实则非常抽象.
3.4“面”的运用

这张图是由六个正多边形闭合而组成的.每个正多边形都赋予相应的颜色.通过颜色的划分将正多边形进行清楚划分,颜色是由黄、绿、青、蓝、紫、红的颜色的循环.每个多边形都是切着图形的一边而构成的.图形也有延展规律,也有色彩循环,每个图形都是无限延展.

从这张图的分析结果来看,中心的圆与其它六个圆是相切的,每个圆圈的色彩仍然是由黄、绿、青、蓝、紫、红等相邻两个圆的重合部分为白色,由内到外的旋转色带效果.
3.5“点”“线”“面”的综合运用
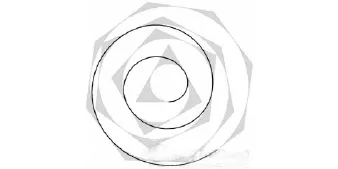
本幅作品是马克思·比尔的点、线、面综合的设计作品,在各个正多边形添入内切圆.内切圆的螺旋方向是沿着正多边形的一边向外螺旋延伸,而渐开线与圆的连线的方向是相反的.双向互相增添了更丰富的效果.
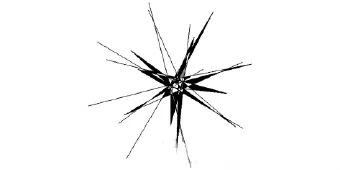
在设计图的外围的放射线上都有黑和白覆盖的区域,而中心的区域是由多边形的对角线构成,形成放射性的绚目效果.
在通过对马克思·比尔作品分析可以看出,马克思·比尔将数学思维运用在整个艺术领域中.在这一系列的作品中,作者将数学规则融入到设计中.其主题是无限延展的线段的组合.作者清楚明了地向大家展示了他将自己的数学规则运用到自己的创作中,并在基础规则中,有以全新的角度赋予在自己的“变异”作品中.用图形、色彩进行全新设计.仅凭审美看的是很难理解其中的规律,只有具有一定的理性思维才能分析出马克思·比尔的作品.我们要用“解析的几何形式”才能理解马克思·比尔的作品.马克思·比尔的作品就体现设计的创造性,作者能将数学思维运用在艺术中.马克思?比尔说过艺术作品来源于纯粹的精神世界.在这个过程中,我们似乎看到了数学与艺术的和谐组合.解读马克思·比尔的作品必须要用纯粹的感知来感受作品,视觉和心理相协调.这是一种真正超脱自然的精神作品.数学思维成为设计手段,表现出绚丽色彩,一切的有规律的设计,看似又无规律,可延展.马克思·比尔的作品是有联系的,运动的.
4 结语——几何的艺术
数模思维是一种理性思维,而艺术是一种感知的表现形式.而马克思·比尔能将数模思维与艺术的表现形式相结合可以说是一个独一无二的创意性的想法.并且马克思·比尔也是将资源进行整合,例如他发现几何的内在规律和图形进行一个巧妙地结合,就变成一幅有节奏感、运动感的设计作品.所以说对资源的整合是设计的一个重要方法.他运用了几何图形,色彩的有序排列,将数学的逻辑思维运用在艺术设计中,用很有规律性、逻辑性的组合运用在艺术图形中.任何一个图形在不断延展中给欣赏者带来更多的想象力.马克思·比尔的作品全新构筑了以数模思维和艺术的表现形式.
马克思·比尔的作品始终围绕数模思维,他将数模思维与平面设计图形相结合是一种创新的设计作品.使得我们在欣赏作品的同时也感受到数学逻辑思维的魅力.看似作品是一种静止,但无限延展又给人一种运动感、节奏感和娘的效果.马克思·比尔的作品运用了规律性的数学语言进行创作,是具体艺术的典型代表,并且将惯有的平面艺术设计推向一个全新的领域与高度.
〔1〕黄厚石,孙海燕.设计原理[M].南京:东南大学出版社,2005.1.
〔2〕[美]H·H·阿纳森[M].西方现代艺术史绘画·雕塑·建筑,天津人民美术出版社,1994.582.
〔3〕转引自http://www.rado.com.cn/press/gallery/artist10.htm.
〔4〕百度百科http://baike.baidu.com.
J05
A
1673-260X(2015)11-0187-03

