国内生产总值预测——基于ARIMA模型的实证分析

冯潇潇

（安徽财经大学 金融学院，安徽 蚌埠 233030）

国内生产总值预测
——基于ARIMA模型的实证分析

冯潇潇

（安徽财经大学 金融学院，安徽 蚌埠 233030）

该文基于ARIMA模型在分析预测不平稳时间序列的独特优势，根据1978-2013年的国内生产总值对2014-2016年的国内生产总值进行预测，预测结果一方面表明模型ARIMA能够很好地拟合我国GDP走势，ARIMA模型是一种精度较高且切实有效的方法模型，另一方面表明我国经济走势较好，这不仅有助于政府制定更加贴合实际的经济金融政策，而且有助于投资者选择更优的个人投资计划.

ARIMA模型；国内生产总值；短期预测

国内生产总值（GDP）是指在一定时期内（一个季度或一年），一个国家所生产出的全部最终产品和劳务的价值.国内生产总值常被用来估测一国的经济发展状况，其走势始终是政府、企业和公众关注的重点.国内学者就曾对GDP的预测进行过研究.华鹏，赵学民（2010）曾通过建立ARIMA模型对广东省生产总值进行了短期预测［1］，王龙兵、陈希镇和王利 （2012）采用ARIMA模型来拟合1991年到2010年的GDP数据并预测之［2］.

人们所建立的回归模型大多都是以经济金融理论为基础的，即根据经济金融理论找出对某变量有影响的其他变量，建立合适的模型，然后收集数据对模型进行估计.但在很多情况下这种建模思想是行不通的，因为根据经济理论对因变量有影响的某些因素我们可能无法观测或度量；或者虽然可以观测或度量，但得到的数据频率可能会大大低于因变量的数据频率.而ARIMA模型的建模思想是不采用其他变量，而是因变量仅对它的滞后值以及随机误差项的现值和滞后值回归，因为因变量之后值、随机误差项的滞后值中已经包含了有关某些我们无法观察的变量对因变量影响的信息，对滞后项回归相当于间接利用了这些信息.利用这种建模思想所得到的模型就是ARIMA模型，下面我们将利用ARIMA模型预测我国未来三年的GDP.

1 ARIMA模型简介以及建模方法［3］

1.1 ARIMA模型的概念

所谓ARIMA模型，是指通过一定的方法先将非平稳时间序列转化为平稳时间序列，然后因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型.在实际中，对于许多不平稳的金融时间数据，我们可以通过差分一次或多次的方法将其转变为平稳序列.如果序列｛｝经过d次差分得到平稳序列｛｝，并且用ARMA（p，q）过程对建立模型，即为一个ARMA（p，q）过程，则我们称为（p，d，q）阶自回归单整移动平均过程，简称ARIMA（p，d，q）.引入滞后算子L， ARIMA（p，d，q）过程可表示为：其中 Ø （L）=1-Ø1L-Ø2L-…-ØpLp，ØL=1+Ø1L+Ø2L2+…+Ø1Lq，｛εt｝为均值为0，方差为的白噪音过程.

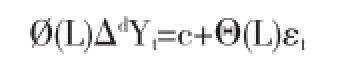
1.2 B-J方法论

在建立ARIMA模型的方法论上时，博克斯和詹金斯率先提出了Box-Jenkins方法论，简称B-J方法论.

该方法论的步骤如下：

步骤1：模型识别.在对模型识别之前，先对原序列进行平稳性检验，若序列是平稳序列，可直接对模型进行识别.若序列不平稳，应首先根据原序列的走势选择相应的变换方法使序列平稳，常用的变换方法有差分变换和对数差分变换，最重要的是确定差分阶d.在ARIMA模型的识别过程中，主要用到自相关函数和偏自相关函数以及它们各自的相关图来确定ARIMA模型的自回归阶数p与移动平均阶数q.

步骤2：模型估计，当确定合适的d，p，q后，下一步便是利用最小二乘法、极大似然法等方法来估计模型中所含自回归和移动平均项系数.

步骤3：模型的诊断检验，即检验所选择的模型是否能够很好地拟合数据，所采用的方法通常是检查应用模型之后的残差序列是否为白噪音过程.若是，则可以认为所选择的模型能够很好地拟合数据；否则需要回到第一步，重新开始.

步骤4：模型预测.ARIMA建模方法得以流行的原因之一就在于它的成功预测.在许多情形下，用ARIMA模型所进行的预测会比传统的结构计量模型得出更可靠的结果，特别是对于短期预测效果更好.

2 应用ARIMA模型对我国GDP进行短期预测

Eviews是专门用于时间序列分析的软件，通过该软件，我们可以很好地发现所研究的时间序列的规律并进行预测.

下面通过建立基于ARIMA的GDP预测模型预测2014年的我国GDP值.

2.1 原始数据分析及预处理

图1 1978-2013年我国GDP曲线

1978年到2013年的GDP数据可以从国家统计局网站上查到.从图1可以看出1978-2013年我国的GDP曲线图是呈指数形式增长的.因此需要对原始数据作一些处理.取原始时间序列的对数形式，并记为lnGDP，再将其一阶差分，将得到的序列记为dlnGDP.应用单位根检验方法检验GDP、lnGDP、dlnGDP的平稳性可以看出GDP、lnGDP不平稳而dlnGDP在5%的显著性水平下是平稳时间序列，因此d=1.

2.2 模型阶数的确定及诊断检验

图2 dlnGDP序列的相关图

从dlnGDP序列的自相关函数图和偏自相关函数图中我们可以观察出，dlnGDP序列的自相关函数是1阶截尾的，偏自相关系函数也是1阶截尾的，所以我们取模型的阶数P=1和q=1，对lnGDP序列建立ARIMA（1，1，1）模型，即对dlnGDP序列建立ARMA（1，1）模型，输出结果如图2.

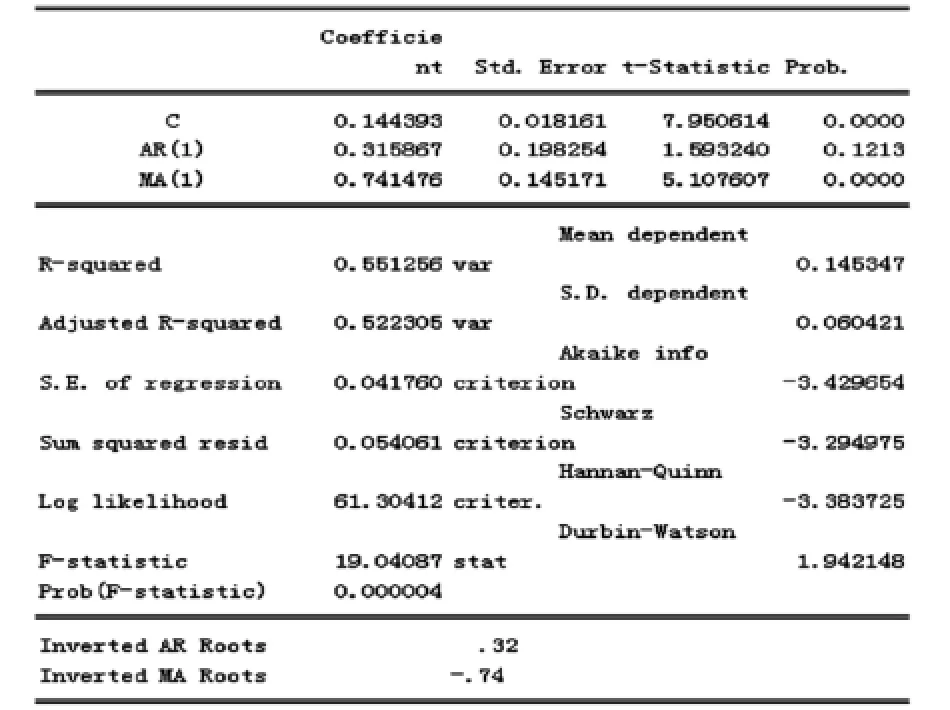
图3 ARIMA（1，1，1）的输出结果

由图3可知，在15%的显著性水平下，该模型的参数都是显著的；AR的特征根和MA的特征根的倒数都在单位圆之内；在eviews的菜单里检验该模型的残差序列可知该残差序列为白噪声过程，如图4所示.因此我们认定模型ARIMA（1，1，1）可以用来拟合序列lnGDP.其方程可以表示为

dlnGDPt=lnGDPt-lnGDPt-1

dlnGDPt=0.144393+0.315867dlnGDPt-1++0.741476

由lnGDP的实际值和预测值以及残差图可以看出该模型的拟合优度是很高的，如图5.

图4 ARIMA（1，1，1）模型残差的相关图

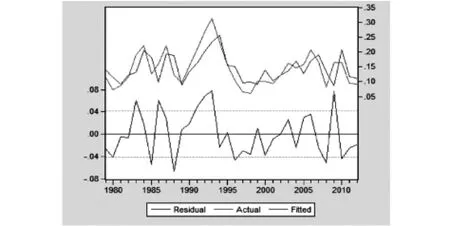
图5 实际值和预测值以及残差

2.3 GDP的预测

基于ARIMA模型的我国GDP预测值2014年为637013亿元，2015年为728745亿元，2016年为839329亿元.

国家统计局于2015年1月20日的公布全年经济数据中国内生产总值为636463亿元，预测值与实际值绝对误差为550亿元，相对误差为0.0864%.由此看出，ARIMA （1，1，1）模型对年度GDP序列具有很好的预测作用.

3 结论

ARIMA过程比ARMA过程在预测不平稳的时间序列数据上更具有优势，比AR和MA过程在回归中所包含的部分更全面，由以上预测和分析结果可知，ARIMA模型确实是一个十分有效的模型.随着时间的推移，在已有的年份数据之后再加上新的数据，还可以继续预测下一期GDP，并且预测结果将更加准确.ARIMA模型的预测作用是十分广泛的.不止GDP，ARIMA还可以用来预测各项投资、储蓄额，这样不仅可以了解我国的经济总量，还可以及时了解我国的经济结构，以便全面把握我国经济运行状况.

〔1〕华鹏，赵学民．ARIMA模型在广东省GDP预测中的应用［J］．统计与决策，2010（12）：166—167.

〔2〕王龙兵，陈希镇，王利.基于ARIMA模型的我国GDP短期预测［J］.科学技术与工程，2012，12（8）.

〔3〕邹平.金融计量学（第二版）［M］.上海：上海财经大学出版社，2010.153-171.

F062.4

A

1673-260X（2015）05-0066-02