推力滚针轴承摩擦力矩特性研究

邓四二，李猛，卢羽佳，代彦宾

（1.河南科技大学机电工程学院，河南洛阳471003；2.浙江兆丰机电股份有限公司，浙江杭州311232）

推力滚针轴承摩擦力矩特性研究

邓四二1，2，李猛1，卢羽佳1，代彦宾1

（1.河南科技大学机电工程学院，河南洛阳471003；2.浙江兆丰机电股份有限公司，浙江杭州311232）

基于滚动轴承动力学理论，建立了推力滚针轴承动力学微分方程，采用精细积分法和预估-校正Adams-Bashforth-Moulton多步法相结合的算法求解其动力学微分方程，在此基础上建立了推力滚针轴承摩擦力矩数学模型。研究了工况参数和结构参数对推力滚针轴承摩擦力矩特性的影响，结果表明：推力滚针轴承摩擦力矩主要分量为滚针-滚道间滑动摩擦，在高速时，保持架-滚针间摩擦也成为主要分量，且较小的兜孔间隙有利于降低轴承摩擦力矩；推力滚针轴承存在一个最佳转速使用范围，使轴承摩擦力矩最小；轴承摩擦力矩与轴向载荷呈正比，且比例系数随着转速的增大而减小；滚针修缘可明显降低轴承摩擦力矩，比较其修缘类型，全凸圆弧修缘滚针更有利于降低轴承摩擦力矩；随着滚针个数和有效长度的增大，轴承摩擦力矩随之增大；随着滚针直径的增大，轴承摩擦力矩减小；应合理优化这些参数，以降低轴承摩擦力矩。

机械学；推力滚针轴承；摩擦力矩；动力学；滚针修缘

0 引言

推力滚针轴承具有轴向刚度大、承载能力强、安装所需空间小等特点，广泛应用于军用车辆的自动变速器等动力传输单元。随着军用车辆动力性能要求越来越高，有效地提高车辆燃油效率已成为发展趋势，而推力滚针轴承作为车辆动力传输单元的重要组成部分，降低推力滚针轴承功耗显得非常重要。

轴承摩擦力矩是产生轴承功耗的根源，国内外学者对滚动轴承摩擦力矩特性做了许多研究:自20世纪50年代起，Palmgren［1］对各种类型和尺寸的轴承进行摩擦力矩试验，并将试验数据回归分析，拟合得到计算轴承摩擦力矩的经验公式。滚针轴承由于其滚子较大的长径比，因而摩擦特性不同于其他类型轴承，Chiu等［2］在试验的基础上提出了向心和推力滚针轴承摩擦力矩的经验计算公式。文献［3-4］分析滚针与滚道不同接触位置的相对滑动和接触区平均压力，在仅考虑滚针-滚道间滑动摩擦情况下，推导出简化的推力滚针轴承摩擦力矩理论计算公式并加以试验验证。Takamizawa等［5］重点研究了滚针与保持架间的摩擦，提出了低摩擦力矩推力滚针轴承的保持架设计方法。国内有关推力滚针轴承的研究［6-7］大多是关于推力滚针轴承滚针-滚道间接触问题的有限元分析，对降低推力滚针轴承摩擦功率损失的研究较少。上述研究针对推力滚针轴承摩擦力矩进行了许多有益的探讨，但上述推力滚针轴承摩擦力矩的经验和理论计算公式仅考虑了滚针-滚道间的滑动摩擦，忽略了推力滚针轴承其他摩擦因素（如滚针与保持架兜孔间摩擦等）和润滑油流变特性对推力滚针轴承摩擦力矩的影响。鉴于此，本文综合考虑推力滚针轴承运转中的摩擦来源和润滑油流变特性，在推力滚针轴承动力学分析的基础上建立推力滚针轴承摩擦力矩数学分析模型，并以某型号推力滚针轴承为例，对轴承使用工况参数和结构参数与轴承摩擦力矩特性关系进行分析，其研究成果可为低摩擦力矩推力滚针轴承的设计提供一定的理论依据。

1 轴承动力学模型

1.1 运动分析

如图1所示，假设轴承座圈固定，轴圈以角速度ωs旋转，保持架和滚针公转角速度为ωc，第j个滚针自转角速度为ωrj.

由图1可得，第j个滚针与轴圈和座圈在半径为y的接触点处相对滑动速度为

图1 滚针与垫圈接触点线速度Fig.1 Linear velocity of contact point between needle and washer

第j个滚针与轴圈和座圈在半径为y的接触点处平均速度为

式中:上标S和H分别代表轴圈和座圈；Dw为滚针直径；dm为轴承节圆直径；l为滚针有效长度。

1.2 轴承内部相互作用力模型

1.2.1 滚针与滚道间接触力

推力滚针轴承在轴向力Fa和倾覆力矩M（或偏心的轴向载荷）作用下，滚针与垫圈间几何位移关系如图2所示。

图2 滚针与垫圈位移与变形示意图Fig.2 Schematic diagram of the displacement between needle and washer

由图2可得，第j个滚针第i片与轴圈接触处的弹性变形量为

式中:Cji为第j个滚针第i片的凸度减少量。

第j个滚针第i片与座圈接触处的弹性变形量为

由此可得每一切片与轴圈和座圈间的法向接触力为

式中:A=1.36η0.9，η为两接触体的综合弹性常数；为考虑各切片间相互影响，第j个滚针第i片与轴圈和座圈接触处弹性变形量的修正系数，具体计算方法参见文献［9］。

第j个滚针与轴圈和座圈间的法向接触力为

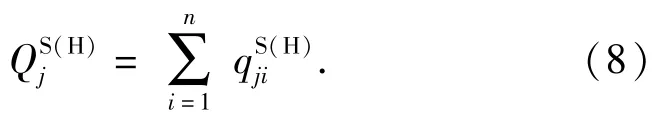
第j个滚针受到的附加力矩为

1.2.2 滚针与滚道间拖动力

由于滚针与滚道不同接触点处线速度不同，且滚针与滚道间的接触负荷分布不均，因此不同接触点处油膜拖动系数也不相同。第j个滚针第i片的油膜拖动系数μji由弹流拖动系数和边界润滑摩擦系数通过油膜参数插值得到［10-11］。

滚针与轴圈和座圈间的拖动力为

由拖动力产生的附加力矩为

1.2.3 滚针与保持架间作用力

滚针与保持架兜孔间的作用力主要考虑滚针与保持架兜孔过梁的流体动压力和由接触变形引起的弹性碰撞力。本文考虑滚针歪斜对滚针与保持架间作用力的影响，使用“切片法”计算滚针与保持架间的作用力。由于滚针与保持架间作用力较小，各切片间相互影响较小，所以采用“经典切片法”，切片方法与上文相同。在轴承运转过程中，滚针与保持架兜孔位移变形关系如图3所示。坐标系OPXpZp为保持架兜孔坐标系，βj为滚针歪斜角，Δzcj为滚针几何中心在兜孔坐标系下的位移。

图3 滚针与保持架兜孔位移变形示意图Fig.3 Schematic diagram of the displacement between roller and cage pocket

由图3可得第j个滚针第i片的几何中心在兜孔坐标系下的位移zcji为

则第j个滚针第i片与保持架间作用力qcji为

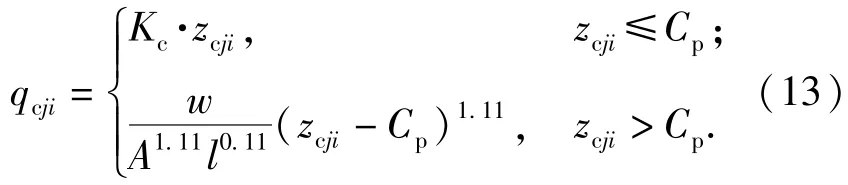
式中:Kc为试验确定的线性逼近常量，对于滚针轴承Kc=67/Cp，Cp=0.5（Dp-Dw）为保持架兜孔间隙，Dp为兜孔直径。第j个滚针第i片与保持架间作用力qcji的方向根据zcji判定，当zcji≥0时，滚针受到保持架的推力，反之，受到保持架的阻力。

滚针与保持架兜孔间作用力Qcj和恢复力矩Mcj为

1.2.4 轴承动力学微分方程

考虑由滚针公转和自转产生的陀螺力矩Mgj= Jrωrj×ωc、离心力和由离心力产生的滚针与上下垫圈间静摩擦力滚针的受力如图4所示。

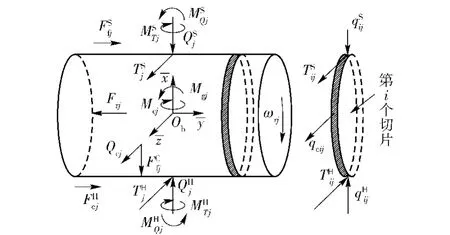
图4 滚针受力示意图Fig.4 Schematic diagram of roller forces

由图4可得第j个滚针的动力学微分方程为

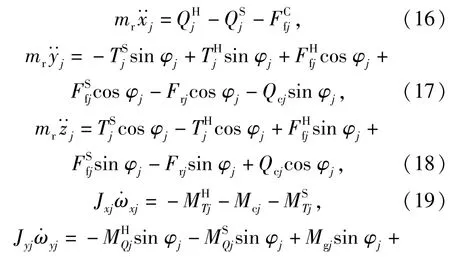
式中:mr为滚针质量；μs、μh为静摩擦系数，与滚针离心力有关；为第j个滚针质心在惯性坐标系｛O；X，Y，Z｝下的线加速度；Jxj、Jyj、Jzj为第j个滚针在惯性坐标系｛O；X，Y，Z｝下的转动惯量；ωxj、ωyj、ωzj为第j个滚针在惯性坐标系｛O；X，Y，Z｝下的角加速度。

2 轴承摩擦力矩

推力滚针轴承运转过程中，引起轴承摩擦力矩的主要因素有滚针与滚道间材料的弹性滞后、滚针与滚道间的滑动摩擦、滚针与滚道间的粘性滚动阻力，滚针与保持架间的摩擦以及油气阻力。这5个因素引起的摩擦力矩之和即为推力滚针轴承摩擦力矩。其各因素的计算公式如下。

2.1 滚针与滚道间弹性滞后引起的摩擦力矩

滚针在轴圈和座圈滚道上滚动时，由于材料的弹性滞后性质产生的能量损失［13］为

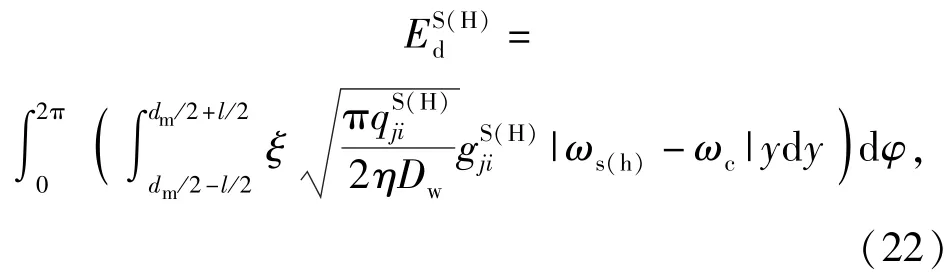
式中:ξ为材料弹性滞后系数，对钢可取ξ=0.01；ωh=0 r/min为轴承座圈转速。

根据能量守恒定律，因滚针与滚道间弹性滞后，引起的推力滚针轴承摩擦力矩分量［14］为

2.2 滚针与滚道间滑动摩擦引起的摩擦力矩

滚针在轴圈和座圈滚道接触处，由相对滑动产生的能量损失为

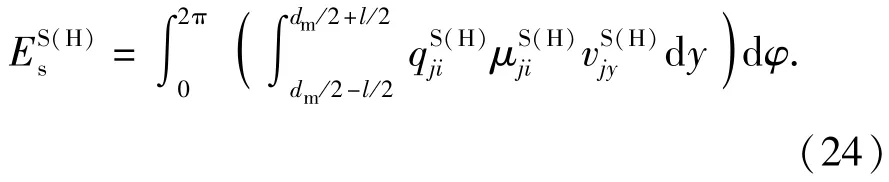
根据能量守恒定律，因滚针与滚道间相对滑动，引起的推力滚针轴承摩擦力矩分量为

2.3 滚针与滚道间粘性滚动阻力引起的摩擦力矩

推力滚针轴承滚针与滚道间粘性滚动阻力引起的能量损失［15］为

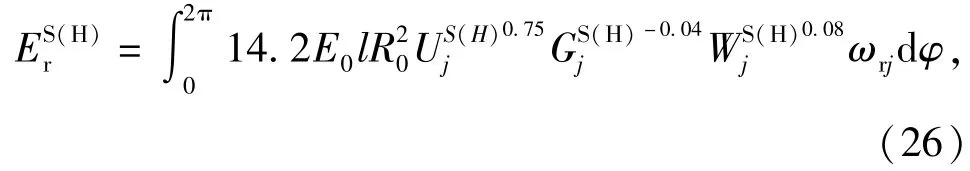
式中:E0是两接触物体的当量弹性模量；R0为等效曲率半径；分别为第j个滚动体与轴圈和座圈的速度参数、材料参数、载荷参数。

根据能量守恒定律，因滚针与滚道间粘性滚动阻力引起的推力滚针轴承摩擦力矩分量为

2.4 保持架兜孔处摩擦引起的摩擦力矩

由滚动体与保持架兜孔间摩擦引起的能量损失为

根据能量守恒定律，因滚针与保持架兜孔间摩擦引起的推力滚针轴承摩擦力矩分量为

2.5 油气阻力引起的摩擦力矩

轴承在旋转过程中，每个滚子在气体混合物中运动时，都会受到油气阻力，此作用力引起的能量损失为

式中:ρm为油气混合物密度；Cd为绕流阻力系数，其具体计算方法参见文献［13］。

根据能量守恒定律，因油气阻力引起的推力滚针轴承摩擦力矩分量为

2.6 轴承总摩擦力矩

将以上轴承各摩擦力矩分量进行叠加，即得到推力滚针轴承总摩擦力矩:

3 轴承摩擦力矩特性分析

在滚动轴承动力学理论的基础上，建立了推力滚针轴承动力学微分方程，采用精细积分法和预估-校正Adams-Bashforth-Moulton多步法相结合的算法求解其动力学微分方程。在此基础上，利用建立的推力滚针轴承摩擦力矩数学模型计算其摩擦力矩。

本文以某型号推力滚针轴承为例，研究工况参数和结构参数对推力滚针轴承摩擦力矩特性的影响。其轴圈、座圈、滚动体材料为GCr15，保持架材料为Q195A，引导方式为自引导。轴承主参数如表1所示。

表1 轴承主参数Tab.1 Main parameters of bearing

一般轴承按照载荷为20%额定动负荷，用经验公式确定最大滚子载荷，进而进行滚子凸度设计。参照文献［13］的标准凸度设计方法，滚针修缘类型和凸度量如表2所示。在本文研究中，滚针采用对数母线修缘。

表2 滚针修缘类型和凸度量Tab.2 The type of crowned needle roller and crowning quantity

3.1 推力滚针轴承摩擦力矩的影响因素

本文所提出的推力滚针轴承摩擦力矩理论计算主要由滚针与滚道间材料的弹性滞后、滚针与滚道间滑动摩擦、滚针与滚道间粘性滚动阻力、滚针与保持架间摩擦以及油气阻力等5个因素所引起的摩擦力矩分量组成。图5为轴向载荷1 000 N时，在不同转速下，推力滚针轴承各摩擦力矩分量的计算值。由图5可以看出，在转速低于2 500 r/min时，由滚针与滚道间滑动摩擦引起的摩擦力矩分量是推力滚针轴承摩擦力矩的主要组成部分，占轴承总摩擦力矩的95%左右，而滚针与滚道间粘性滚动阻力，滚针与保持架间的摩擦，材料的弹性滞后，以及油气阻力引起的摩擦力矩分量对轴承总摩擦力矩影响依次减小；随着轴承转速的提高，滚针与滚道间的滑动摩擦依然是影响轴承摩擦力矩的主要因素，但由滚针与保持架间摩擦引起的摩擦力矩分量迅速增大，特别是在高速时，约占轴承总摩擦力矩的30%，而由滚针与滚道间粘性滚动阻力、油气阻力和材料的弹性滞后引起的摩擦力矩依次减小。因此，对于低摩擦力矩推力滚针轴承的设计，应注重减小滚针与滚道间的滑动摩擦，在高速条件下，也应考虑保持架结构参数的设计，以减小滚针与保持架间摩擦，进而减小轴承摩擦力矩。

图5 推力滚针轴承各摩擦力矩分量计算值Fig.5 Calculated components of friction torques of needle roller thrust bearings

3.2 工况参数对推力滚针轴承总摩擦力矩的影响

3.2.1 转速对总摩擦力矩的影响

图6为轴向载荷1 000 N时，推力滚针轴承转速对摩擦力矩的影响。由图6可以看出，随着轴承转速的提高，轴承摩擦力矩呈现先减小再增加的趋势。这是由于在较低的转速时，滚针与滚道间润滑油膜尚未形成，滚针与滚道间滑动摩擦系数较大，随着轴承转速的增大，润滑油膜逐渐形成，滚针与滚道滑动摩擦系数逐渐减小，所以轴承摩擦力矩减小。当轴承转速继续增大时，润滑油引起的粘性滚动阻力、滚针与保持架间的摩擦阻力和油气阻力等也随之增大，从而造成轴承摩擦力矩随轴承转速的继续增加而迅速增大。因此，推力滚针轴承存在一个最佳的转速使用范围。由于转速为影响推力滚针轴承摩擦力矩重要的工况参数，在以下研究中，选取500 r/min、2 500 r/min和4 000 r/min分别代表推力滚针轴承的低、中、高3种转速条件，分析在这3种转速条件下，其他参数对推力滚针轴承摩擦力矩特性的影响。

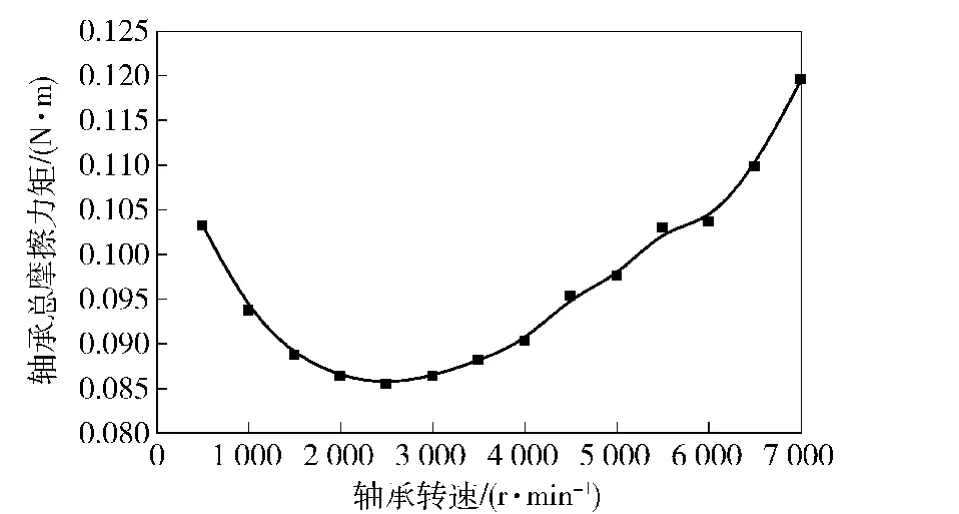
图6 轴承转速对轴承总摩擦力矩的影响Fig.6 Effect of rotating speed on bearing friction torque

3.2.2 轴向载荷对总摩擦力矩的影响

图7为在3种转速条件下，轴向载荷对轴承摩擦力矩的影响。由图7可以看出，在3种转速条件下，随着轴向载荷的增大，轴承摩擦力矩也随之增加，轴向载荷与轴承摩擦力矩基本呈正比，这与文献［4］的推力滚针轴承摩擦力矩试验结果是一致的。但不同转速条件下，轴向载荷与摩擦力矩间的比例系数并不相同，随着轴承转速的增大而减小，这主要是由于随着轴承转速增大，滚针与滚道间润滑油膜厚度增加，其滑动摩擦系数减小，进而使比例系数减小。

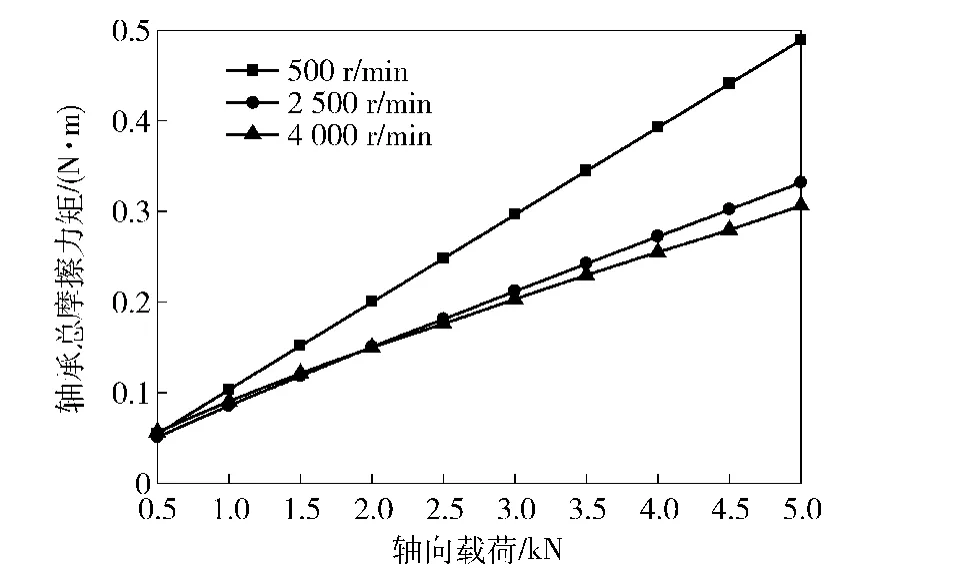
图7 轴向载荷对轴承总摩擦力矩的影响Fig.7 Effect of axial force on bearing friction torque

3.3 结构参数对推力滚针轴承总摩擦力矩的影响

3.3.1 滚针修缘类型对总摩擦力矩的影响

图8为轴向载荷1 000N时，在3种转速条件下，不同滚针修缘类型对轴承摩擦力矩的影响。由图8可以看出，在3种转速条件下，滚针修缘可明显降低推力滚针轴承的摩擦力矩，这是由于滚针修缘有利于减小滚针两端的接触负荷，进而减小由滚针两端的滑动摩擦引起的能量损失，因此可明显降低轴承摩擦力矩。由于不同修缘类型的滚针沿轴线方向接触负荷分布不同，所以修缘类型对轴承摩擦力矩影响很大，当滚针修缘类型为全凸圆弧修缘时，轴承摩擦力矩最小，当滚针修缘类型分别为圆心在中心圆弧修缘，圆心在两侧圆弧修缘和对数母线修缘时，轴承摩擦力矩依次增大。因此，在满足推力滚针轴承承载能力的条件下，应尽量选择全凸圆弧修缘类型的滚针，以降低推力滚针轴承摩擦力矩。

图8 滚针修缘类型对轴承总摩擦力矩的影响Fig.8 Effect of needle roller crowned type on the bearing friction torque

3.3.2 滚针有效长度对总摩擦力矩的影响

图9为轴向载荷1 000 N时，在3种转速条件下，滚针有效长度对轴承摩擦力矩的影响。由图9可知，在3种转速条件下，随着滚针有效长度的增大，轴承摩擦力矩呈线性增大趋势，这是由于随着滚针有效长度的增加，滚针两端的相对滑动加剧，由滑动摩擦产生的能量损失增大，因此推力滚针轴承的摩擦力矩呈增大趋势。这与文献［4］的推力滚针轴承摩擦力矩试验结果相一致。因此在设计低摩擦力矩推力滚针轴承时，应综合考虑轴承使用条件，合理确定滚针有效长度，以降低推力滚针轴承摩擦力矩。

图9 滚针有效长度对轴承总摩擦力矩的影响Fig.9 Effect of effective length of needle roller on bearing friction torque

3.3.3 滚针个数对摩擦力矩的影响

图10为轴向载荷1 000 N时，在3种转速条件下，滚针个数对轴承摩擦力矩的影响。从图10中可以看出，在3种转速条件下，随着滚针个数的增加，轴承摩擦力矩呈缓慢增大趋势，这是由于随着滚针个数的增多，滚针所受的润滑油粘性滚动阻力和油气阻力增大，但这两部分对轴承摩擦力矩贡献较小，因此轴承摩擦力矩增加的幅度较小；在高速条件下，当滚针个数达到一定数量时，轴承摩擦力矩急剧增大，这是由于随着滚针数量的增多，滚针与保持架间耦合作用增强，滚针与保持架频繁接触，进而导致滚针与保持架间摩擦阻力急剧增大，所以轴承摩擦力矩急剧增加。因此，在设计低摩擦力矩推力滚针轴承时，特别是在高速条件下，应尽量使滚针个数小于一定数量。

图10 滚针个数对轴承总摩擦力矩的影响Fig.10 Effect of needle roller number on bearing friction torque

3.3.4 滚针直径对总摩擦力矩的影响

图11为轴向载荷1 000 N时，在3种转速条件下，滚针直径对轴承摩擦力矩的影响。由图11可以看出，在3种转速条件下，随着滚针直径的增大，轴承的摩擦力矩也随之降低。这是由于较大的滚针直径，有利于润滑油膜的形成，使滚针与滚道间的滑动摩擦系数减小，进而降低推力滚针轴承的摩擦力矩。因此，在满足轴承安装空间的条件下，应尽量选择较大的滚针直径，以降低推力滚针轴承的摩擦力矩。

图11 滚针直径对轴承总摩擦力矩的影响Fig.11 Effect of diameter of needle roller on bearing friction torque

3.3.5 保持架兜孔间隙对轴承总摩擦力矩的影响

图12为轴向载荷1 000 N时，在3种转速条件下，保持架兜孔间隙对轴承摩擦力矩的影响。由图12可知，在低、中速条件下，保持架兜孔间隙对轴承摩擦力矩几乎没有影响，这主要是由于在低、中速条件下，影响轴承摩擦力矩的主要因素为滚针与滚道间的滑动摩擦，而保持架与滚针间摩擦对轴承摩擦力矩影响很小。在高速条件下，随着保持架兜孔间隙的增大，轴承摩擦力矩呈增大趋势，这主要是由于随着兜孔间隙的增大，滚针在兜孔中的歪斜加剧，滚针两端与保持架兜孔间接触更加频繁，导致滚针与保持架兜孔间的能量损失增大，进而使轴承摩擦力矩增大。因此，设计高速低摩擦力矩推力滚针轴承时，在保证滚针在保持架兜孔中不被卡死的前提下，应尽量选取较小的兜孔间隙，以减小推力滚针轴承的摩擦力矩。

图12 保持架兜孔间隙对轴承总摩擦力矩的影响Fig.12 Effect of cage pocket clearance on bearing friction torque

3.4 对比验证

采用Hatazawa等［3］所进行的推力滚针轴承总摩擦力矩试验对本文分析模型进行对比验证。其试验轴承主参数为:滚针直径2.0 mm，滚针有效长度4.3 mm，轴承节圆直径40 mm，滚针个数24个，润滑油型号为机械油ISO VG10.在轴向载荷5 000 N，转速分别为500 r/min、1 000 r/min、2 000 r/min的条件下，本文计算结果和文献［3］试验结果对比如表3所示。由表3可知，本文计算结果与文献［3］试验结果基本相符，在不同转速条件下，轴承摩擦力矩误差率小于7%，说明本文所建立的模型能准确地描述推力滚针轴承的摩擦力矩特性。产生误差的主要原因是许多重要的参数如润滑油温度等，在文献［3］试验中并没有给出，而是假设与本研究中的部分参数一致。

表3 计算结果与试验结果对比Tab.3 Comparison of calculated results

4 结论

本文基于滚动轴承动力学理论，建立了推力滚针轴承动力学微分方程，在此基础上建立推力滚针轴承摩擦力矩数学模型。并以某型号推力滚针轴承为例，研究工况参数和结构参数对推力滚针轴承摩擦力矩特性的影响，得出以下结论:

1）推力滚针轴承摩擦力矩主要分量为滚针与滚道间的滑动摩擦。在高速时，滚针与保持架间的摩擦也成为轴承摩擦力矩的主要组成部分，且较小的保持架兜孔间隙有利于降低轴承摩擦力矩。

2）推力滚针轴承存在一个最佳的转速使用范围，使轴承摩擦力矩最小；轴承摩擦力矩与轴向载荷呈正比，且随着轴承转速的增大，其比例系数逐渐减小。

3）滚针修缘可明显降低轴承摩擦力矩，比较其修缘类型，全凸圆弧修缘滚针更有利于降低轴承摩擦力矩。因此在满足轴承承载能力条件下，应尽量选择全凸圆弧修缘滚针，以降低轴承摩擦力矩。

4）随着滚针个数和有效长度的增大，轴承摩擦力矩也随之增大，随着滚针直径的增大，轴承摩擦力矩减小。因此应根据具体的工况条件和安装空间，合理优化这些参数，以降低轴承摩擦力矩。

（

）

［1］ Palmgern A.Ball and roller bearing engineering［M］.Burbank，Philadephia:SKF Industries，Inc，1969.

［2］ Chiu Y P，Myers M.A rational approach for determining permissible speed for needle roller bearings［J］.SAE Transactions，1998，107（2）:330-337.

［3］ Hatazawa T，Kawaguchi T，Kagami J.Frictional characteristics of needle roller thrust bearing:part 1 and 2［J］.Japanese Journal of Tribology，2003，48（5）:453-471.

［4］ Hatazawa T，Kawaguchi T.Frictional torque of needle roller thrust bearing［J］.Tribology Transactions，2009，52（1）:127-132.

［5］ Takmizawa W，Toyama M，Sato H，et al.Development of lowfriction-torque thrust needle roller bearing［J］.Journal of Lubrication Technology，1979，101（3）:293-326.

［6］ 郑志坚，潘伶.基于ANSYS的推力滚子轴承接触分析［J］.福州大学学报:自然科学版，2009，37（2）:224-227. ZHENG Zhi-jian，PAN Ling.Contact analysis of thrust roller bearing based on ANSYS［J］.Journal of Fuzhou University:NaturalScience Edition，2009，37（2）:224-227.（in Chinese）

［7］ 乔淑香，邓四二，高银涛，等.基于ANSYS的推力滚针轴承垫圈应力分析［J］.轴承，2009（5）:40-42. QIAO Shu-xiang，DENG Si-er，GAO Yin-tao，et al.Strain stress analysis to washer of needle roller thrust bearing based on ANASYS［J］.Bearing，2009（5）:40-42.（in Chinese）

［8］ Harris T A.The effect of misalignment on the fatigue life of cylindrical roller bearings having crowned rolling members［J］.Journal of Lubrication Technology，1969，2（4）:294-300.

［9］ Yang H S，Cheng G D，Deng S E，et al.Analysis of the rollerrace contact deformation of cylindrical roller bearing using a improved slice method［C］//International Conference on Mechatronic Science，Electric Engineering and Computer.Jilin:IEEE，2011: 711-714.

［10］ Tomoya S，Kazayoshi H.Dynamic analysis of cage behavior in a tapered roller bearing［J］.Journal of Tribology，2006，128（3）: 604-611.

［11］ 王燕霜，邓四二，杨海生，等.滚/滑接触中HKD航空润滑油拖动特性试验研究［J］.兵工学报，2009，30（7）:958-961. WANG Yan-shuang，DENG Si-er，YANG Hai-sheng，et al.A-nalysis of traction characteristics of HKD aviation lubricating oil in rolling/sliding contacts［J］.Acta Armamentarii，2009，30（7）: 958-961.（in Chinese）

［12］ 杜辉，周彦伟，邓四二，等.高速圆柱滚子轴承零件间相互作用力瞬态动力学分析［J］.轴承，2005（9）:9-12. DU Hui，ZHOU Yan-wei，DENG Si-er，et al.Transient dynamics analysis on interaction between components of high speed cylindrical roller bearings［J］.Bearing，2005（9）:9-12.（in Chinese）

［13］ 邓四二，贾群义.滚动轴承设计原理［M］.北京:中国标准出版社，2008. DENG Si-er，JIA Qun-yi.Rolling design principles［M］.Beijing:Standards Press of China，2008.（in Chinese）

［14］ 邓四二，李兴林，汪久根，等.角接触球轴承摩擦力矩特性研究［J］.机械工程学报，2011，47（5）:114-120. DENG Si-er，LI Xing-ling，WANG Jiu-gen，et al.Frictional torque characteristic of angular contact ball bearings［J］.Journal of Mechanical Engineering，2011，47（5）:114-120.（in Chinese）

［15］ Matsuyama H.High efficiency and tribology in rolling bearings［J］.JTEKT Engineering Journal:English Edition，2012，1009E:108-113.

Study of Friction Torque of Needle Roller Thrust Bearings

DENG Si-er1，2，LI Meng1，LU Yu-jia1，DAI Yan-bin1
（1.School of Mechatronics Engineering，Henan University of Science and Technology，Luoyang 471003，Henan，China；2.Zhejiang ZhaoFeng Mechanical and Electronic Co.，Ltd.，Hangzhou 311232，Zhejiang China）

The dynamic differential equations of needle roller thrust bearings are established based on the dynamic theory of rolling bearings.The precise integration method and the predicting-correcting Adams-Bashforth-Moulton multistep method are used to solve the equations，and the friction torque mathematic models of needle roller thrust bearings are built.The influences of working conditions and structural parameters on the friction torque of needle roller thrust bearings are investigated.The results show that the slip friction between roller and raceway is main component of the friction torque of needle roller thrust bearings.the friction between cage and roller also becomes the main component at high speed，and a small pocket clearance is in favor of reducing the friction torque.An optimal speed can be selected，which makes the friction the smallest.The friction torque is in direct proportion to the axial load，and the proportional coefficient decreases with the rise of rotating speed of bearings.The roller profile modification can reduce the friction torque evidently，the full arc profile modification is the most propitious to reduce the friction torque compared to crowned shapes.the friction torque increases with the rise of roller number and effective length，and the friction torque decreases with the rise of the roller diameter.Theseparameters should be rationally optimized to reduce the friction torque.

mechanics；needle roller thrust bearing；friction torque；dynamics；roller profile modification

TH133.33

A

1000-1093（2015）07-1347-09

10.3969/j.issn.1000-1093.2015.07.026

2014-10-26

国家“十二五”科技攻关项目（JPPT-125-171）；河南省科技创新人才计划项目（144200510020）

邓四二（1963—），男，教授，博士生导师。E-mail:dse@haust.edu.cn；李猛（1989—），男，硕士研究生。E-mail:limengbearing@126.com