火箭助飞鱼雷不同齐射方式下的捕获概率分析

田恒斗，侯代文，房毅，孙文豪

（91439部队，辽宁大连116041）

火箭助飞鱼雷不同齐射方式下的捕获概率分析

田恒斗，侯代文，房毅，孙文豪

（91439部队，辽宁大连116041）

针对火箭助飞鱼雷打击远距离目标时捕获概率大幅下降的问题，依据其对目标搜索方式及反潜作战的特点，提出了一种与传统“同一点齐射”不同的“人工散布齐射”方式；并基于全概率的基本思想，构建了描述两种齐射方式捕获概率的数学解析模型；计算了打击目标前置点和现在点两种典型作战样式下，二者在不同射击距离上的捕获概率。计算值与仿真实验结果吻合良好，表明在远距离上打击目标现在点时，人工散布齐射的捕获概率优于同一点齐射。

概率论；火箭助飞鱼雷；齐射方式；人工散布；捕获概率

0 引言

火箭助飞鱼雷是一种集鱼雷技术和导弹技术于一体的远程反潜武器，它利用助飞火箭使鱼雷在空中高速飞行至目标区域，然后伞降入水对目标潜艇实施搜索、跟踪和攻击［1］。相对于传统的反潜鱼雷，其具有速度高、射程远、突击能力强和发射平台安全性好等诸多突出优势，从而成为了世界各国竞相发展的热点，相关的作战使用研究也取得了众多成果［2-5］。文献［2-3］的研究结果均表明，单枚火箭助飞鱼雷对远距离目标射击时，其捕获概率会大幅下降。对此，在作战使用中常采用多雷齐射的方式以提高其作战效果［4］。不过，针对火箭助飞鱼雷齐射方式下对目标捕获概率模型的研究，目前尚鲜有文献报道。

有鉴于此，为进一步丰富火箭助飞鱼雷的作战使用理论及方法研究，在文献［4］提出的瞄准同一点齐射方式的基础上，本文提出了一种火箭助飞鱼雷人工散布齐射方式；并采用全概率的基本思想，对这两种不同的齐射方式，构建形式上统一的齐射捕获概率数学解析模型，再针对每种齐射方式，分别形成完整的计算解析式；又依据火箭助飞鱼雷打击目标“前置点”和“现在点”［5］两种不同作战样式时目标散布规律的不同，具体计算分析了这两种典型作战样式下，人工散布齐射和同一点齐射在不同射击距离上的捕获概率，并与仿真实验结果对比，以初步检验所得解析模型及计算结果的正确性。

1 两种齐射方式的基本概念

火箭助飞鱼雷齐射是指发射两枚或两枚以上火箭助飞鱼雷对同一目标进行射击，且使鱼雷同时（或在较短的时间间隔内）抵达预定入水点，并同时对目标潜艇展开搜索和攻击的射击方式［4］。

文献［4］中的齐射方式，其核心思想是各枚火箭助飞鱼雷均瞄准目标散布中心这同一点进行射击，故本文将其称之为“同一点齐射”。

火箭助飞鱼雷能有效搜索捕获目标潜艇的区域可等效为以其入水点为圆心的一个圆形区域［3］。显然，采用同一点齐射时，各枚鱼雷的搜索域存在较大重叠。而反潜作战中，通常仅需一枚鱼雷命中目标，即可对潜艇构成致命毁伤。故在目标散布范围较大时，如果科学地分开设置各枚鱼雷的入水点，可以形成覆盖范围更大的联合搜索域，则有可能进一步提高火箭助飞鱼雷齐射的作战效果。据此，本文提出了如图1所示的“人工散布齐射”方式（以两雷齐射为例），即将每枚火箭助飞鱼雷的射击瞄准点T1、T2人为地偏离目标散布中心E某一距离L，从而形成一个更大的有效搜索区域，以提高至少一枚鱼雷捕获目标的概率。

2 两种齐射方式的捕获概率模型

为计算分析上述两种齐射方式在不同作战样式下的捕获概率，下面将首先采用全概率的基本思想，构建形式上统一的齐射捕获概率基本模型，再针对每种齐射方式具体细化其解析模型。为便于建模，下文中描述目标散布和鱼雷落点散布的各解析式均建立在以目标散布中心为原点，以真北方向为y轴正方向，以正东为x轴正方向的直角坐标系下。

图1 人工散布齐射示意图Fig.1 Artificial scatter salvo mode of rocket-assisted torpedoes

2.1 齐射捕获概率的基本模型

在目标散布范围内其位于坐标（x，y）点的概率可由其目标分布密度函数fE（x，y）表示。且目标分布具有互不相容性，即目标若位于（x，y）点则不可能再出现在其他位置点上。又设目标位于（x，y）点时，被至少一枚鱼雷捕获的条件概率为PTE（x，y）.则根据连续型全概率公式［6］，火箭助飞鱼雷齐射方式下目标被捕获的概率P可表示为

式中:积分区间Ω为目标散布范围；fE（x，y）依据所采取的作战样式（打击目标“前置点”或“现在点”）确定。

（1）式即为可同时描述同一点齐射和人工散布齐射两种方式下捕获概率的基本模型。当然，该式也可表示单雷射击时的捕获概率。下面具体分析两种齐射方式下，条件概率PTE（x，y）的计算方法。

2.2 同一点齐射的PTE（x，y）

根据文献［3］，对火箭助飞鱼雷而言，如果目标位于其捕获圆内，则认为该雷能够捕获目标。显然，该条件等价于鱼雷落入以目标位置点（x，y）为圆心，以鱼雷捕获圆半径R为半径的圆域内。所以一枚鱼雷捕获目标的概率p0等于该雷落入上述圆域内的概率。为便于与目标点（x，y）区分，以（ε，η）代表鱼雷落点，则p0可表示为

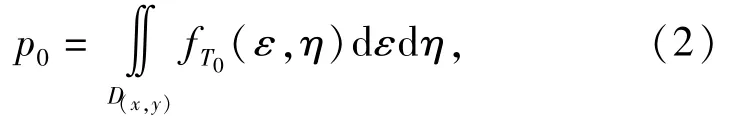
式中:积分区间D（x，y）为

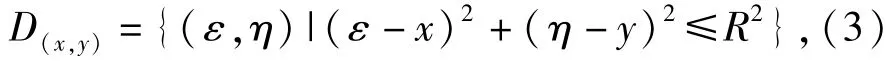
式中:捕获圆半径R由文献［3］中的方法计算确定；fT0（ε，η）为描述鱼雷落点散布的分布密度函数。同一点齐射方式下鱼雷瞄准目标散布中心射击，其落点散布中心为坐标原点，服从二维正态分布，fT0（ε，η）可表示为［2］

式中:σT为鱼雷落点散布均方差。

而同一点齐射方式下，各枚鱼雷落点散布中心均为坐标原点，其落点分布密度函数一致，又因为积分区间D（x，y）相同，则各雷对目标的捕获概率p0也一致。故该齐射方式下至少一枚鱼雷捕获目标的概率PTE（x，y）可表示为

式中:n为发射鱼雷的枚数。

2.3 人工散布齐射的PTE（x，y）

采用人工散布齐射时，设第i枚鱼雷的瞄准点为（ai，bi），则其落点分布密度函数fTi（ε，η）为

相应的该枚鱼雷对目标的捕获概率pi为

且积分区间D（x，y）同（3）式。则该齐射方式下至少一枚鱼雷捕获目标的概率PTE（x，y）为

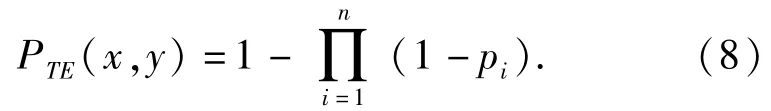
综合（1）式～（8）式，即构建出了计算同一点齐射和人工散布齐射两种方式下对目标捕获概率的数学解析模型。下文将针对打击目标“前置点”和“现在点”两种典型作战样式下，目标分布密度函数fE（x，y）的区别，具体计算分析两种齐射方式在不同射击距离上的捕获概率。

3 对“前置点”齐射的捕获概率

3.1 对“前置点”射击时的fE（x，y）

在本文坐标系下，对目标前置点射击时，目标散布中心为坐标原点。又根据文献［3］的分析，目标位置点（x，y）与坐标原点的偏差（Δx，Δy）可表示为

式中:vE、β为目标的航速、航向；t为从发射舰接收目标指示到鱼雷入水的时间，包括系统反应时间和鱼雷飞行时间，其中飞行时间可近似为射击距离Df与鱼雷空中飞行速度vf的比值；ΔvE、Δβ为相应的航速、航向误差；（Δx0，Δy0）为解算射击诸元时依据的目标初始位置点误差，均由探测平台对目标运动要素的观测误差引起。

式中:X=（x，y）T；Kφ为协方差矩阵，

3.2 对“前置点”不同齐射方式的捕获概率

下面以两枚鱼雷齐射为例，基于前述构建的解析模型，采用数值积分的方法计算打击目标“前置点”时，两种齐射方式在不同射击距离上获得的捕获概率。其中，人工散布射击的瞄准点分别设定为（0.5R，0）、（-0.5R，0）.为与文献［3］中单雷射击的捕获概率值对比分析，计算中所涉及鱼雷和目标的其他相关参数均与文献［3］一致。在射击距离［15 km，50 km］区间内，两种齐射方式捕获概率的计算结果如图2所示，为便于对比将文献［3］中单雷对前置点射击时的捕获概率值一并绘于图2中。

同时，为了初步检验本文解析模型的正确性，进行基于蒙特卡洛法的计算机模拟仿真实验。仿真实验中，两枚鱼雷同时对目标展开搜索，其中任意一枚鱼雷捕获目标即判定目标被捕获，该次仿真实验成功，两枚鱼雷均耗尽航程且都未捕获目标，判定该次仿真实验失败，每一状态下仿真实验做2 000次［9］。其中单枚鱼雷对目标搜索过程的仿真程序及参数设置与文献［3］一致。仿真实验结果亦绘制于图2中。

由图2可见，仿真实验结果与解析模型计算值吻合良好，其偏差不大于5%，初步证明了在打击目标前置点这种作战样式下，本文所得齐射捕获概率解析模型的正确性。由图2中计算结果可见，在打击目标前置点时，采用同一点齐射方式，对目标的捕获概率高于单雷射击，且随射击距离的增加，提高的幅度变大，在50 km的最大射击距离处，捕获概率提高7%左右。在文中设置的人工散布射击瞄准点条件下，人工散布射击方式的捕获概率值小于同一点齐射方式，略大于单雷射击的捕获概率。

图2 不同齐射方式对“前置点”射击的捕获概率Fig.2 Calculated acquisition probabilities at prepositive point in different salvo modes

进一步的计算分析表明，调整人工散布射击瞄准点与目标散布中心的距离L，会改变其捕获概率。L分别取0.2R、0.5R、0.8R时，人工散布射击的捕获概率如图3所示。由图3可见，对目标前置点射击时，人工散布齐射的散布距离L越小，其捕获概率越高，但仍小于同一点齐射方式的捕获概率；且散布距离L过大时（如图3中L=0.8R），人工散布齐射的捕获概率反而小于单雷射击的捕获概率。故在打击目标前置点作战样式下，不宜采用人工散布齐射方式。

图3 对“前置点”射击时不同散布距离下人工散布齐射的捕获概率Fig.3 Acquisition probabilities at different scatter ranges at prepositive point in artificial scatter salvo mode

4 对“现在点”齐射的捕获概率

4.1 对“现在点”射击时的fE（x，y）

在打击目标现在点作战样式下，因目标的航速、航向均未知，为确定其分布密度函数fE（x，y），需先对目标的航速、航向做出一定假设。当前相关领域研究中，通常有如下两种方式:一是假设目标航速、航向都服从均匀分布［10-12］；二是假设目标航速服从瑞利分布，航向服从均匀分布［13-14］。下面分别讨论两种假设条件下，对应的目标分布密度函数fE（x，y）.

1）假设目标航速服从［0，vEmax］区间内的均匀分布，航向服从［0，2π］区间内的均匀分布。根据文献［10-12］的研究，该假设条件下，目标散布服从以其初始位置点为圆心，以vEmaxt为半径的圆域内的均匀分布。其中，vEmax为目标最大可能航速，t为从接收目标指示到鱼雷入水的时间。则在本文坐标系下，描述现在点射击方式时目标散布的分布密度函数fE（x，y）为

2）假设目标航速服从以常规潜艇经济航速vE（或核动力潜艇的一般航速）为均值的瑞利分布，航向服从［0，2π］区间内的均匀分布。根据文献［13-14］的研究结论，该假设条件下，目标散布服从二维正态分布，在本文坐标系下可表示为

式中:σE0为目标初始位置点散布误差，与（12）式、（13）式中的σx0、σy0含义一致，可取σE0=σx0=σy0；t仍为从接收目标指示到鱼雷入水的时间。

4.2 对“现在点”不同齐射方式的捕获概率

下面仍以两枚鱼雷齐射为例，采用与前述3.2节相同的解析计算和模拟仿真方法及相关参数，分析打击目标“现在点”时，在前述两种不同的目标航速分布假设条件下，两种齐射方式在不同射击距离上的捕获概率。

4.2.1 目标航速服从均匀分布

取目标最大可能航速与文献［3］中一致，vEmax=24 kn；人工散布齐射的散布距离L取1/2的目标散布圆半径，即两枚鱼雷瞄准点分别为（0.5vEmaxt，0）、（-0.5vEmaxt，0）.模拟仿真实验中，目标航向、航速在［0，2π］和［0，vEmax］内按均匀分布生成，目标初始位置按二维正态分布生成。

在上述设置条件下，所得解析计算和仿真实验结果如图4所示，文献［3］中单雷对现在点射击的捕获概率也一并绘于图中。

图4 目标航速均匀分布假设下不同齐射方式对“现在点”射击的捕获概率Fig.4 Acquisition probabilities at current point in different salvo modes based on uniform distribution of target velocity

调整人工散布射击瞄准点与目标散布中心的距离L，分别取为0.2、0.5、0.8倍的目标散布圆半径时，目标航速服从均匀分布假设情况下，人工散布射击在不同射击距离上的捕获概率如图5所示。

图5 目标航速均匀分布假设下对“现在点”射击时不同散布距离L对应的捕获概率Fig.5 Acquisition probabilities at different L at current point based on uniform distribution of target velocity

由图5可见，射击瞄准点相对目标散布中心的散布距离L，显著影响人工散布射击方式的捕获概率。在文中设置条件下，L=0.5vEmaxt时人工散布射击的效果相对最优，L=0.2vEmaxt时其效果降低但仍优于同一点齐射，在L=0.8vEmaxt时虽优于单雷射击，但其捕获概率已低于同一点齐射。

4.2.2 目标航速服从瑞利分布

目标航速取常规潜艇经济航速vE=10 km/h［14］，人工散布射击的瞄准点分别设定为（0.5R，0）、（-0.5R，0）。模拟仿真实验中，目标航速按均值为vE的瑞利分布生成，其他参数设置同上。

在上述设置条件下，所得解析计算和仿真实验结果如图6所示。目标航速服从瑞利分布时，单雷对现在点射击捕获概率的结果也一并绘于图6中。

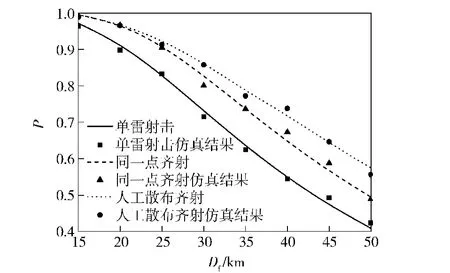
图6 目标航速瑞利分布假设下不同齐射方式对“现在点”射击的捕获概率Fig.6 Acquisition probabilities at current point in different salvo mode based on Rayleigh distribution of target velocity

L分别取0.2R、0.5R、0.8R时，目标航速服从瑞利分布假设情况下，人工散布射击在不同射击距离上的捕获概率如图7所示。

图7 目标航速瑞利分布假设下对“现在点”射击时不同散布距离L对应的捕获概率Fig.7 Acquisition probabilities at different L at current point based on Rayleigh distribution of target velocity

由图7可见，在目标航速服从瑞利分布假设条件下，射击瞄准点散布距离L对人工散布射击方式捕获概率的影响更为复杂。在文中设置条件下，L= 0.5R时人工散布射击的效果仍相对最优；L=0.2R时其效果降低但仍优于同一点齐射；但当L=0.8R时，其变化较为复杂，在小于22 km的射击距离内，其捕获概率甚至小于单雷射击的捕获概率，在大于35 km的距离上其捕获概率开始优于L=0.2R的捕获概率，特别是当射击距离大于45 km时，其捕获概率出现了超过L=0.5R对应捕获概率的趋势。

4.2.3 两种目标航速假设条件下不同齐射方式射击效果的综合比较

综合图4、图6可见，在打击目标现在点时，两种目标航速分布假设条件下，解析模型计算值与仿真实验结果均吻合良好。由图4、图6中结果均可见，在打击目标现在点时，采用同一点齐射和人工散布齐射方式，对目标的捕获概率均高于单雷射击。特别是采用人工散布齐射时，随射击距离的增加，捕获概率提高的幅度显著增加；在对应的人工散布射击瞄准点条件下，图4所示目标航速采用均匀分布假设时，50 km的射击距离上相对于单雷射击其捕获概率提高近25%；图6所示目标航速采用瑞利分布假设时，相同射击距离上捕获概率提高近17%。综合对比分析两种不同齐射方式在不同射击距离上的捕获概率可见，两种目标航速分布假设条件下，在大于30 km的较远距离上，人工散布齐射的捕获概率均高于同一点齐射的值，且随射击距离的增加，优势更为明显。在文中设定的人工散布射击瞄准点条件下，在50 km射击距离上，图4所示的目标航速采用均匀分布假设时，人工散布齐射的捕获概率高出同一点齐射10%左右；图6所示的目标航速采用瑞利分布假设时，人工散布齐射高于同一点齐射8%左右。

同时，综合图5、图7可见，在打击目标现在点作战样式下，采用人工散布齐射方式时，存在一个最佳的散布距离。特别是在目标航速服从瑞利分布假设的条件下，对应不同的射击距离其最佳的瞄准点散布距离L不同。并且，最佳散布距离L还应受鱼雷齐射数量、鱼雷自导作用距离、鱼雷落点精度、以及目标最大可能航速等诸多因素的共同影响。鉴于问题的复杂性，限于文章篇幅，宜在后续研究中进行更详细深入的专门论述。

5 结论

本文在传统的“同一点齐射”方式基础上，根据反潜作战及火箭助飞鱼雷对目标搜索方式的特点，提出了一种新的火箭助飞鱼雷“人工散布齐射”方式。为定量分析两种齐射方式的捕获概率，基于全概率的基本思想，构建了形式上统一的齐射捕获概率基本模型，并针对每种齐射方式，分别形成了完整的计算其捕获概率的数学解析式。又针对打击目标“前置点”和“现在点”两种典型作战样式，具体计算了人工散布齐射和同一点齐射在不同射击距离上的捕获概率，且计算值与仿真实验结果吻合良好，初步表明了所得解析模型的正确性。综合分析计算结果可知，相对于单雷射击，在打击目标前置点时，采用同一点齐射方式可使捕获概率获得一定程度的提高，而不宜采用人工散布齐射方式；而在打击目标现在点作战样式下，特别是目标距离较远时，人工散布齐射方式的优势十分显著。

当然，本文通过建模、计算和仿真研究，仅是提出了火箭助飞鱼雷人工散布射击的基本思想和模型，并初步论证了其有效性，而对不同条件下最优散布参数选择的原则和方法等问题，后续还将进行深化研究，以为火箭助飞鱼雷作战使用提供一种有效的方法。同时，现有模型尚未考虑目标规避、水声对抗等因素，也有待后续更深入的研究和完善。

（

）

［1］ 薛晓中，邵大燮，金友兵.火箭助飞鱼雷的弹道分析［J］.兵工学报，2001，22（4）:452-455. XUE Xiao-zhong，SHAO Da-xie，JIN You-bing.Ballistic characteristics of rocket assisted torpedo［J］.Acta Armamentarii，2001，22（4）:452-455.（in Chinese）

［2］ 周明，徐德民，刘影，等.溅落点散布误差对火箭助飞鱼雷射击效率影响研究［J］.系统工程理论与实践，2007，27（9）: 153-158. ZHOU Ming，XU De-min，LIU Ying，et al.Infection of impact dispersion to the rocket assisted torpedo fire efficiency［J］.Systems Engineering-Theory&Practice，2007，27（9）:153-158.（in Chinese）

［3］ 田恒斗，曹庆刚，侯代文，等.火箭助飞鱼雷捕获概率的解析模型［J］.兵工学报，2013，34（7）:916-921. TIAN Heng-dou，CAO Qing-gang，HOU Dai-wen，et al.Analytical model of rocket-assisted torpedo's acquisition probability［J］. Acta Armamentarii，2013，34（7）:916-921.（in Chinese）

［4］ 门金柱，周明，郑亚波.双舰齐射火箭助飞鱼雷协同攻潜研究［J］.鱼雷技术，2010，18（4）:316-320. MEN Jin-zhu，ZHOU Ming，ZHENG Ya-bo.Simulation of rocket assisted torpedo salvo attack from a two-warship formation［J］. Torpedo Technology，2010，18（4）:316-320.（in Chinese）

［5］ 周明，徐德民.火箭助飞鱼雷对随机机动目标的射击效率仿真［J］.火力与指挥控制，2007，32（4）:116-119. ZHOU Ming，XU De-min.Study on fire efficiency for attacking random maneuvering target by the rocket-assisted torpedo［J］.Fire Control and Command Control，2007，32（4）:116-119.（in Chinese）

［6］ 盛骤，谢式千，潘承毅.概率论与数理统计［M］北京:高等教育出版社，2008. SHENG Zhou，XIE Shi-qian，PAN Cheng-yi.Probability theory and mathematical statistics［M］.Beijing:Higher Education Press，2008.（in Chinese）

［7］ 寇祝，周明.基于超视距通道的火箭助飞鱼雷射击效率研究［J］.鱼雷技术，2009，17（2）:57-60. KOU Zhu，ZHOU Ming.Study on fire efficiency of rocket-assisted torpedo based on over-the-horizon fire channel［J］.Torpedo Technology，2009，17（2）:57-60.（in Chinese）

［8］ 邢昌风，李敏勇，吴玲.舰载武器系统效能分析［M］.北京:国防工业出版社，2008. XING Chang-feng，LI Min-yong，WU Ling.Effectiveness analysis of shipborne weapon system［M］.Beijing:National Defense Industry Press，2008.（in Chinese）

［9］ 孟庆玉，张静远，宋保维.鱼雷作战效能分析［M］.北京:国防工业出版社，2003. MENG Qing-yu，ZHANG Jing-yuan，SONG Bao-wei.Torpedo operational effectiveness analysis［M］.Beijing:National Defense Industry Press，2003.（in Chinese）

［10］ 赵晓哲，沈治河.海军作战数学模型［M］.北京:国防工业出版社，2004. ZHAO Xiao-zhe，SHEN Zhi-he.Mathematical model of naval operation［M］.Beijing:National Defense Industry Press，2004.（in Chinese）

［11］ 陈玉文.海面机动目标散布规律及反舰导弹搜索区的划分［J］.飞航导弹，1999，29（7）:6-10. CHEN Yu-wen.Sea-surface target spreading regularity and the search area division of anti-ship missile［J］.Aerodynamic Missile Journal，1999，29（7）:6-10.（in Chinese）

［12］ 戚学文，严建钢，谢宇，等.直升机吊放声纳应召搜潜模型［J］.火力与指挥控制，2014，39（3）:47-50. QI Xue-wen，YAN Jian-gang，XIE Yu，et al.Study on antisubmarine searching models of dipping sonar carried by helicopters［J］.Fire Control and Command Control，2014，39（3）:47-50.（in Chinese）

［13］ 屈也频.反潜飞机搜潜效能评估与决策建模［M］.北京:国防工业出版社，2011. QU Ye-pin.Effectiveness evaluation and decision modeling on searching submarine of antisubmarine aircrafts［M］.Beijing:National Defense Industry Press，2011.（in Chinese）

［14］ 蒋志忠，杨日杰，张林琳，等.基于先验目标分布的磁探仪应召搜潜最佳圆周搜索半径研究［J］.兵工学报，2011，32（9）:1099-1105. JIANG Zhi-zhong，YANG Ri-jie，ZHANG Lin-lin，et al.Study on optimal circle search radius of magnetic anomaly detector on call based on priori target distribution［J］.Acta Armamentarii，2011，32（9）:1099-1105.（in Chinese）

Analysis of Acquisition Probability of Rocket-assisted Torpedo in Different Salvo Modes

TIAN Heng-dou，HOU Dai-wen，FANG Yi，SUN Wen-hao
（Unit 91439 of PLA，Dalian 116041，Liaoning，China）

The acquisition probability declines dramatically when the rocket-assisted torpedoes attack a distant target.To solve this problem，the salvo mode of artificial scatter，which is different from traditional salvo，is presented according to the searching mode of rocket-assisted torpedo and the features of antisubmarine operation.The analytical models for two kinds of salvo modes are developed based on the basic idea of total probability.The acquisition probabilities at different shooting ranges under the operation modes of attacking the prepositive point and current point of torpedo are calculated by two models，respectively.The results agree well with the simulation test results.When the current point shooting mode is adopted，the acquisition probability using the salvo mode of artificial scatter is higher than that by traditional salvo at long shooting range.

probability theory；rocket-assisted torpedo；salvo mode；artificial scatter；acquisition probability

TJ630

A

1000-1093（2015）07-1370-07

10.3969/j.issn.1000-1093.2015.07.029

2014-08-01

总装备部预先研究项目（51314020301）

田恒斗（1981—），男，工程师。E-mail:wudi19820314@foxmail.com