利用单相跳闸后信息的输电线路单相接地单端精确测距方法

耿建昭 王 宾 董新洲

（清华大学电机系电力系统及发电设备安全控制和仿真国家重点试验室 北京 100084）

0 引言

故障测距方法根据所用电气量数量的不同，可以分为单端法[1,2]和双端法[3,4]，根据所用原理的不同可以分为阻抗法和行波法[5]。双端法在原理上能够实现故障精确测距，但经济性差，而且不适用于单端供电或多 T接输电线路。单端行波法因难以有效识别故障点反射波头，并未大面积推广应用。实际中单端阻抗法因稳定、简单、经济而被广泛应用。

传统的单端阻抗测距方法受到过渡电阻和对端系统的影响，测距精度较差[1,2,6-9]。主要难点在于对故障支路电流或电压相位的精确估计，文献[10]提出了利用测量点负序电流估计故障点相位的单端测距方法，该方法较传统的采用零序电流或相电流估算方法，其测距精度有很大提高，但对于两端系统阻抗角相差很大的情形仍存在较大误差。而且以上的估计方法均为近似方法，无法获得故障距离在理论上的精确解。

在超、特高压输电线路上，90%以上的故障都是单相接地故障，普遍采用综合重合闸方式[11]。基于此，文献[12]提出了基于 R-L模型的单相重合闸线路故障测距方法，利用断路器单相跳闸后非全相运行信息计算对端系统阻抗实现单端精确测距，为单端阻抗测距提供了新思路，但该方法利用R-L模型，未考虑线路分布电容、相间耦合、潜供电流等因素影响，不适用于分布参数特性明显的高压输电线路，因此论文故障测距精度的提高也有限。

针对以上问题，本文利用故障后以及单相跳闸后的信息，基于分布参数建模，并考虑单相跳闸后故障相与健全相相间耦合的影响，提出了一种新单端测距方法。该方法能够利用单端电气量精确计算出包括对端系统电动势、系统阻抗、故障距离和过渡电阻在内的所有网络未知参数，实现了单相接地故障的单端精确测距。

1 利用单相跳闸后信息的输电线路单相接地故障单端测距方法

1.1 过渡电阻和对端系统的影响

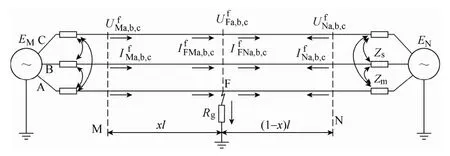
假设如图1所示的系统在输电线路F点发生A相接地故障。

基于传统集中参数模型，线路M端故障相电压UMA可以表示为

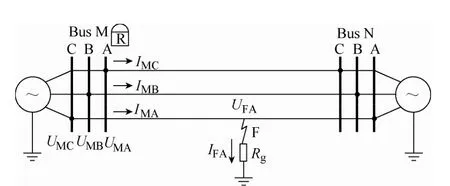
图1 输电线路单相接地故障示意图Fig.1 SLGF at F point in a transmission line

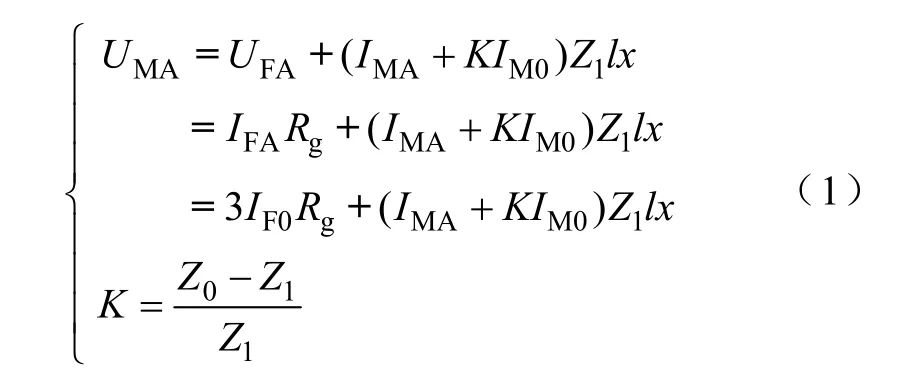
式中，UFA为故障点电压；IMA和IM0为M端故障相电流和零序电流；IFA和IF0分别为故障支路相电流和零序电流；Rg为过渡电阻；Z0、Z1分别为单位长度线路零序和正序阻抗；l为线路全长；x为故障距离百分比。式中IFA无法通过测量得到的，其值受到 N端系统电动势和阻抗的影响，仅通过式（1）无法求得故障距离x。现存的单端阻抗方法多利用M端测量的零序（负序）电流估测故障支路电流IFA（IF0）的相位，以期在IFA的过零点通过式（1）计算故障距离。但是IFA的相位亦受到对端系统阻抗的影响，如图2所示。

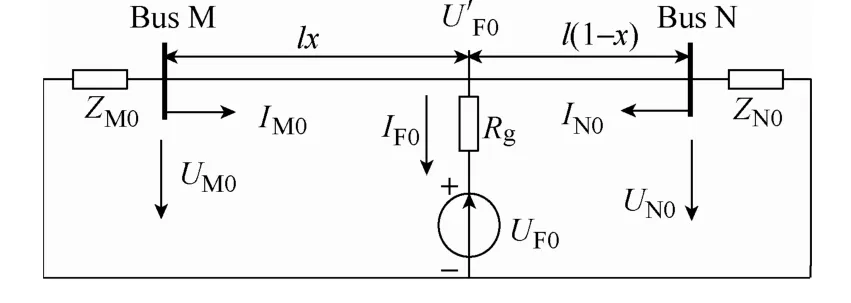
图2 单相接地零序等效电路Fig.2 Zero-sequence equivalent system configuration

图2中IM0和IF0的关系可表示为

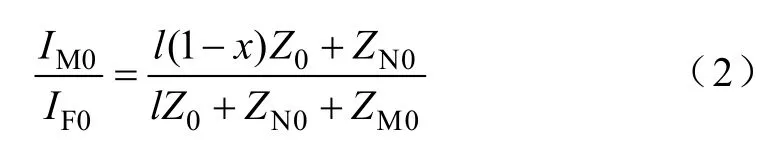
式中，ZN0和ZM0分别表示N和M端等值系统的零序阻抗。由式（2）可知，当ZN0绝对值很小（N为强系统），而且阻抗角与ZM0的阻抗角相差较大时，用IM0估计IF0的相位将存在较大误差。因此，仅利用故障后电气量的单端阻抗测距方法均为近似算法，受到过渡电阻和对端系统阻抗的影响，精度很难提高。

1.2 算法基本思路

高压输电线路单相接地故障采用单相跳闸，1s后重合闸的运行方式，以保证系统的稳定性和供电可靠性。单相跳闸后，系统的拓扑结构将发生改变，从而可以为故障测距提供额外信息，综合故障后跳闸前以及单相跳闸后两个时间断面的信息，便可实现单相接地故障单端精确测距。

本文方法将故障距离、过渡电阻、对端系统电动势、对端系统阻抗均视为未知参数，通过求解系统方程获得所有参数的精确解。发生单相接地故障时，系统方程可列写为

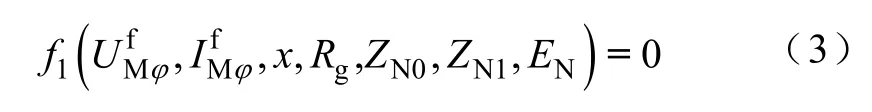
式中，f1为由系统结构决定的一组表达式；和为M侧电压电流测量值；EN为N端系统故障相电动势；ZN1为N端系统等效正序阻抗。

故障相跳闸后，系统方程可列写为

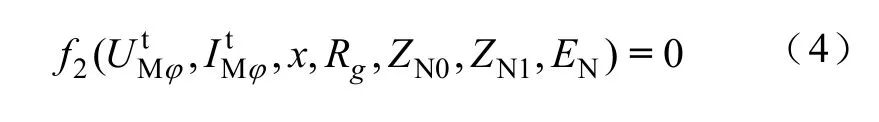
式中，f2为由跳闸后系统结构决定的一组表达式；和跳闸后 M 侧电压电流测量值。联立式（3）和式（4），就可解出包括故障距离在内的所有系统未知参数，但需遵循如下假设：

（1）故障为永久性故障，在故障后单相跳闸前和单相跳闸后过渡电阻Rg保持恒定。

（2）由于故障后跳闸前以及跳闸后两个时间断面信息仅间隔几个工频周波，因此假定N端系统电动势和阻抗保持不变。

1.3 方程的具体推导

本方法采用分布参数线路模型以考虑分布电容的影响。首先给出符号说明如下。

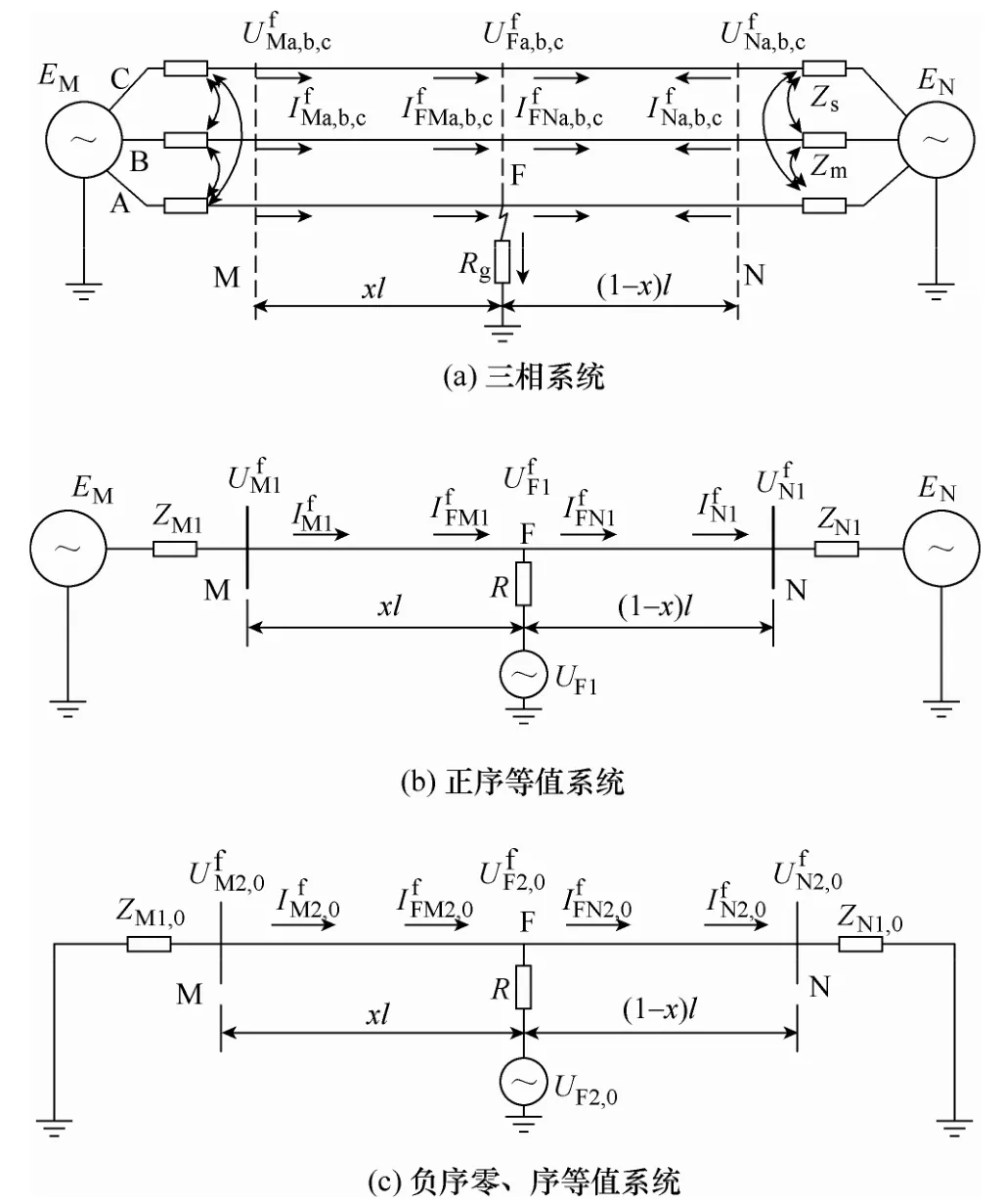
图3 基于分布参数的输电线路单相接地故障示意图Fig.3 SLGF at the F point in a distributed parameter transmission line

Zc0、Zc1为线路零序和正序波阻抗；γ0、γ1为线路零序和正序传播系数；sinh、cosh为双曲正弦和双曲余弦函数；α为相序变换旋转因子，α=0.5+j/2。

1.3.1单相接地故障后跳闸前阶段

发生单相接地故障的系统除故障点外，其他部分仍三相对称，如图3a所示，因此可以利用相序变换将系统解耦，如图3b和图3c所示。

把故障距离x和过渡电阻Rg作为未知参数，则线路 N端的电压电流可用首端电流电压测量量表示为

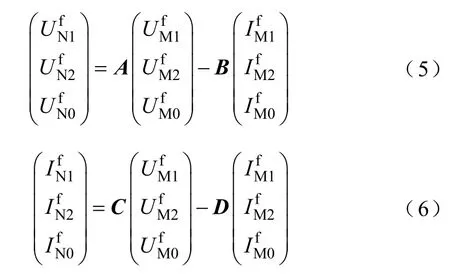
式中，A、B、C、D分别为3×3的系数矩阵，如式（7）～式（10）所示，具体推导请见附录。线路N端的边界条件可以用式（11）表示。

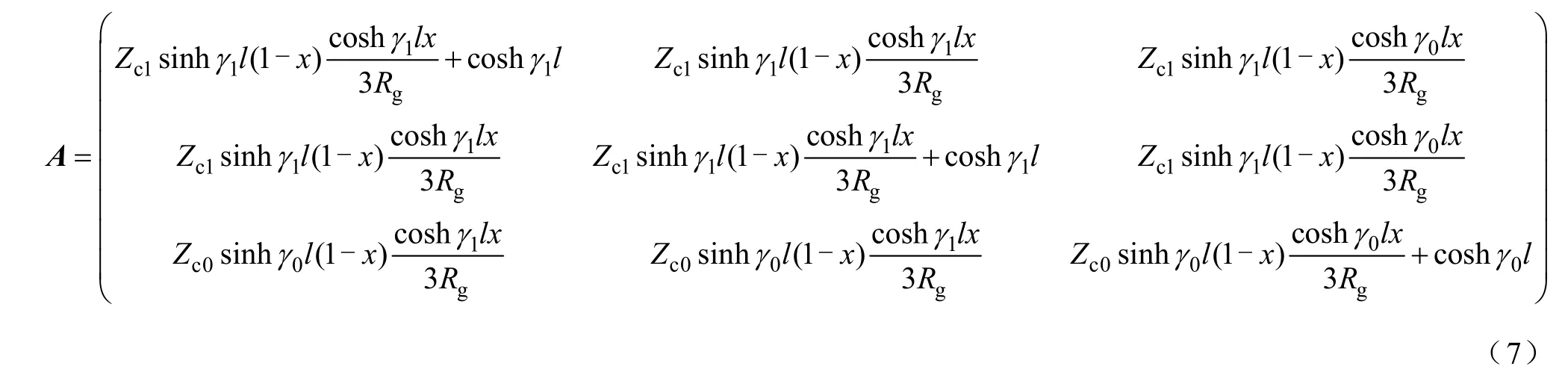
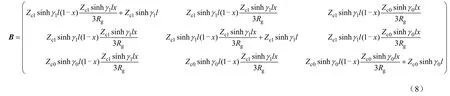
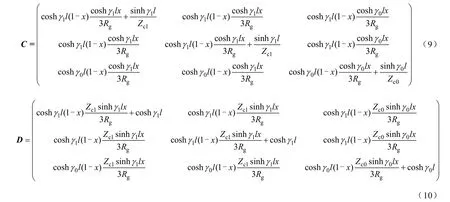
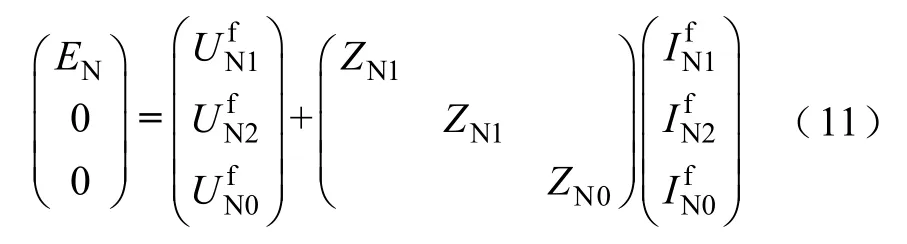
式（5）、式（6）和式（11）即为式（3）所示的系统方程的具体形式。

1.3.2单相跳闸后阶段

故障相断路器从线路两端跳闸后的系统结构图如图4所示。

虽然系统结构发生了变化，但由于线路首末端电压电流关系只与测量点之间的系统结构有关，因此仍然满足

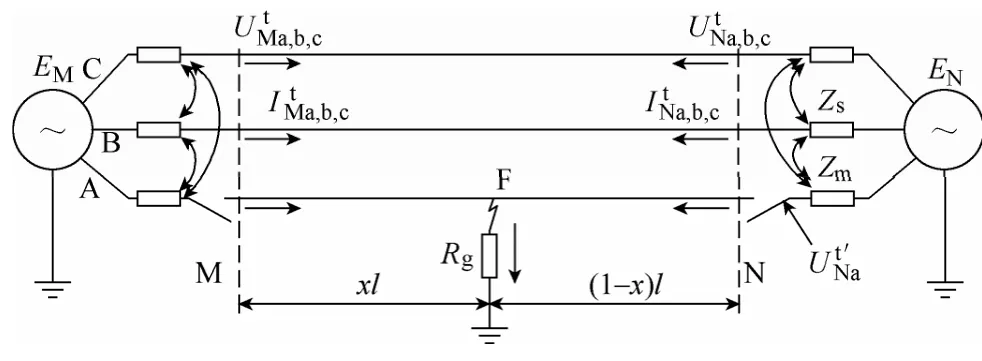
图4 单相跳闸后的系统示意图Fig.4 System during post-single-phase-trip

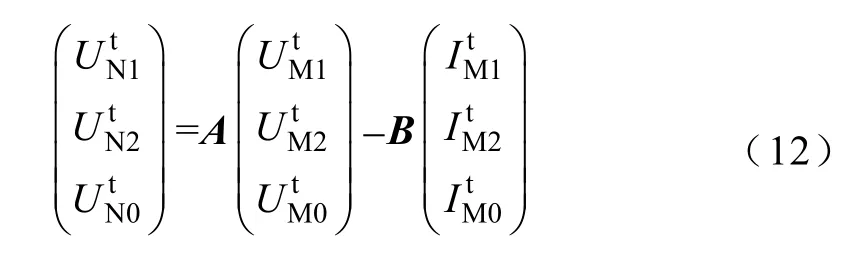
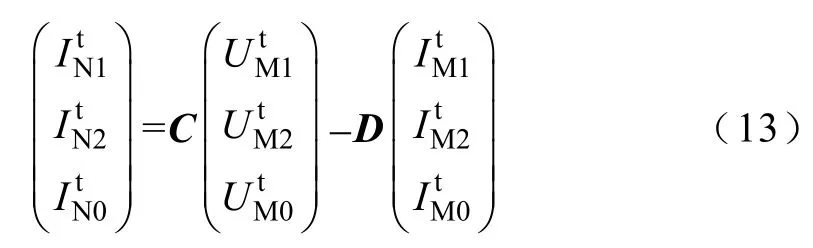
式中，A、B、C、D的含义与式（5）和式（6）中相同。与跳闸前的区别仅仅在于N端的边界条件发生了变化，可表示为

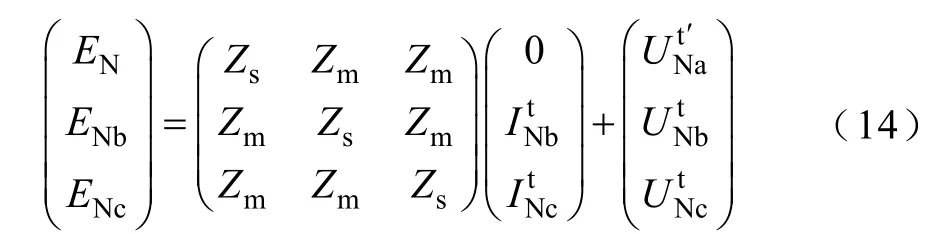
式中，ENb和ENc分别为N端系统B、C相电动势；Zs、Zm分别为N端系统的自阻抗和相间互阻抗；为N端母线侧的故障相电压，由于断路器已跳开，与线路侧故障相电压并不相等。式（14）中的相变量与序变量的关系可以表示为

综合式（14）～式（17），用 N端线路侧电压电流序量表示的边界条件表示为

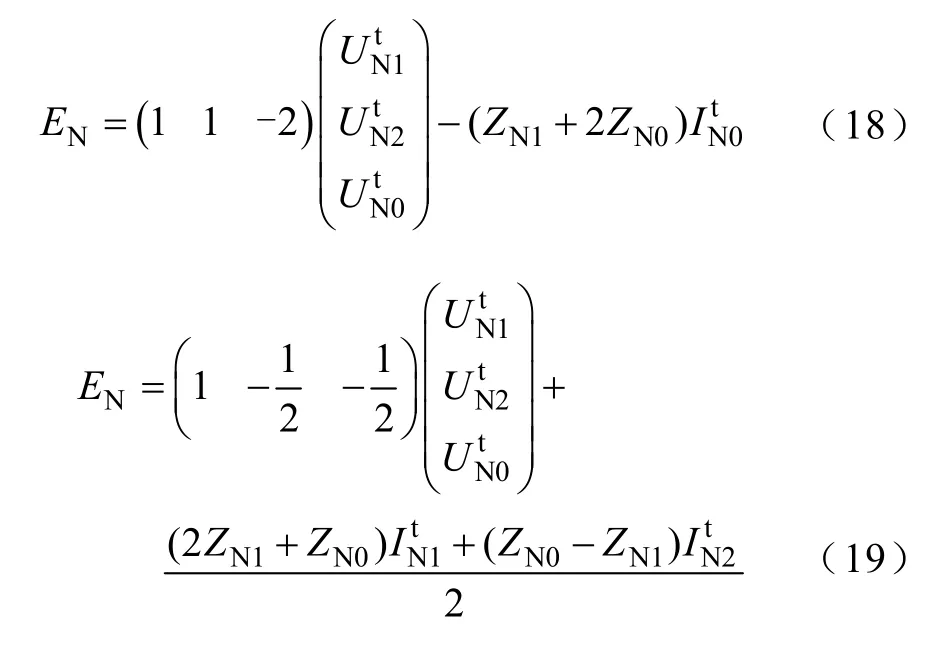
式（12）、式（13）和式（18）、式（19）即为式（4）所示的跳闸后系统方程的具体形式。

联立式（5）、式（6）、式（11）～式（13）、式（18）和式（19）即可求得故障距离、过渡电阻、N端系统的电动势、正序和零序阻抗等所有网络未知参数。

1.4 利用单相跳闸后信息的单相接地故障单端测距方法

求取式（5）、式（6）、式（11）～式（13）、式（18）和式（19）组成的方程组的解析解比较困难，因此本文选用迭代方法求解，具体步骤如下：

（1）设定故障距离x和过渡电阻Rg的初值，如设x=0，Rg=1Ω。

（3）将步骤（2）中求得的ZN1和ZN0代入式（11）的第一个方程，求得故障后N端系统故障相电动势，为与后续结果区分，此处记作。

（5）计算误差值F(x,Rg)

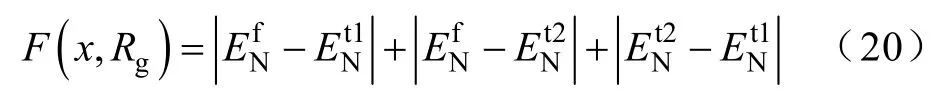
（6）以步长Δx和ΔR分别增加x和Rg，重复步骤（2）～（5），遍历所有的故障距离和过渡电阻组合，求得误差最小值所对应的x和Rg即为故障距离和过渡电阻真实值。

以上计算中，所用的故障后电压电流和跳闸后电压电流在时间上相差0.02s的整数倍；故障距离x的范围为[0,1]，Δx越小计算结果越精确，但同时会增大计算量，本文中Δx取 0.005；考虑到过渡电阻值一般在几欧姆到几百欧姆之间，Rg的范围设为[1,1 000] Ω，ΔR取为1Ω，总共需要201×1 000次迭代，用2.1GHz主频的笔记本电脑约需30s得到测距结果。故障测距算例测如图5所示。

2 算法性能验证

2.1 算法性能验证概述

对所提算法，基于EMTP-ATP 软件进行仿真验证，分析了不同故障距离、不同过渡电阻、不同负载情况以及不同系统阻抗对算法精度的影响。

图5 迭代误差F(x, Rg)收敛于故障点示意图，400km长的线路在距首端150km发生经100Ω过渡电阻的单相接地故障Fig.5 Demonstration ofF(x,Rg),a 150km,100Ω single-phase-to-earth fault in a 400km line

仿真模型结构与图3a所示相同，系统参数借鉴晋东南—荆门1 000kV特高压输电线路参数[10]，线路长度从 100km变化至 500km，EM和EN分别为1.106 2倍和1.106 9倍的额定电压，EN落后44°。不同线路长度所得测距结果基本一致，因此以下分析中以线路长度400km为例，线路参数和系统阻抗见表1。

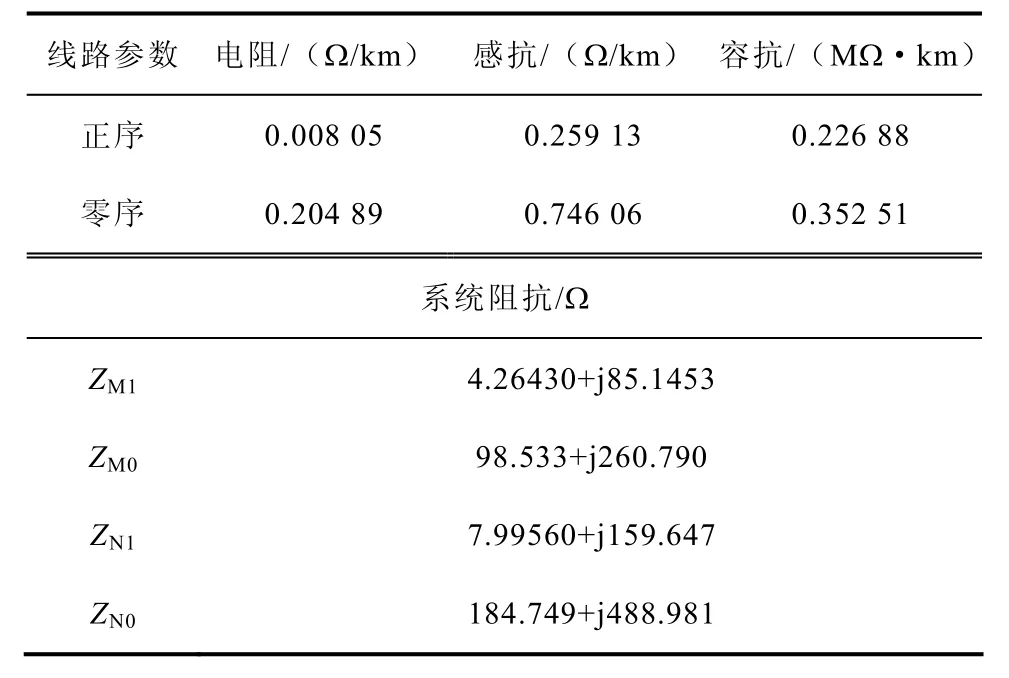
表1 1 000kV系统参数Tab.1 Parameters for 1 000kV simulation system

2.2 故障距离的影响

故障距离从距首端 2km一直增长到距首端399km，步长为10km左右，过渡电阻固定为120Ω，部分测距结果见表2。

2.3 过渡电阻的影响

过渡电阻值分别设为5Ω、10 Ω、50 Ω、100 Ω和 200 Ω，用于仿真低阻、中阻和高阻故障，不同故障距离，不同过渡电阻下的误差曲线如图 6所示。

表2 不同故障距离的测距结果Tab.2 Location results under different fault distances

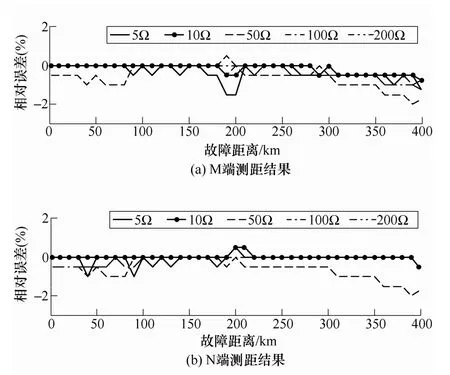
图6 测距误差曲线Fig.6 Relative error of the proposed algorithm

由图6可见，绝大多数测距结果相对误差小于1%，最大误差出现在长故障距离、大过渡电阻（200 Ω）情况，误差约为2%。造成误差的主要因素一方面在于故障的暂态过程使得电压电流相量的计算存在误差，另一方面在于EMTP-ATP的计算机制：仿真计算中，首末端的电压电流并不完全满足式（5）、式（6）和式（12）、式（13）所示的传输方程，最恶劣情况下存在接近2%的误差。

2.4 负载的影响

改变EM和EN的夹角以仿真不同的负载情况，过渡电阻设为50 Ω，其他参数与表1中相同，M侧测距结果见表3。

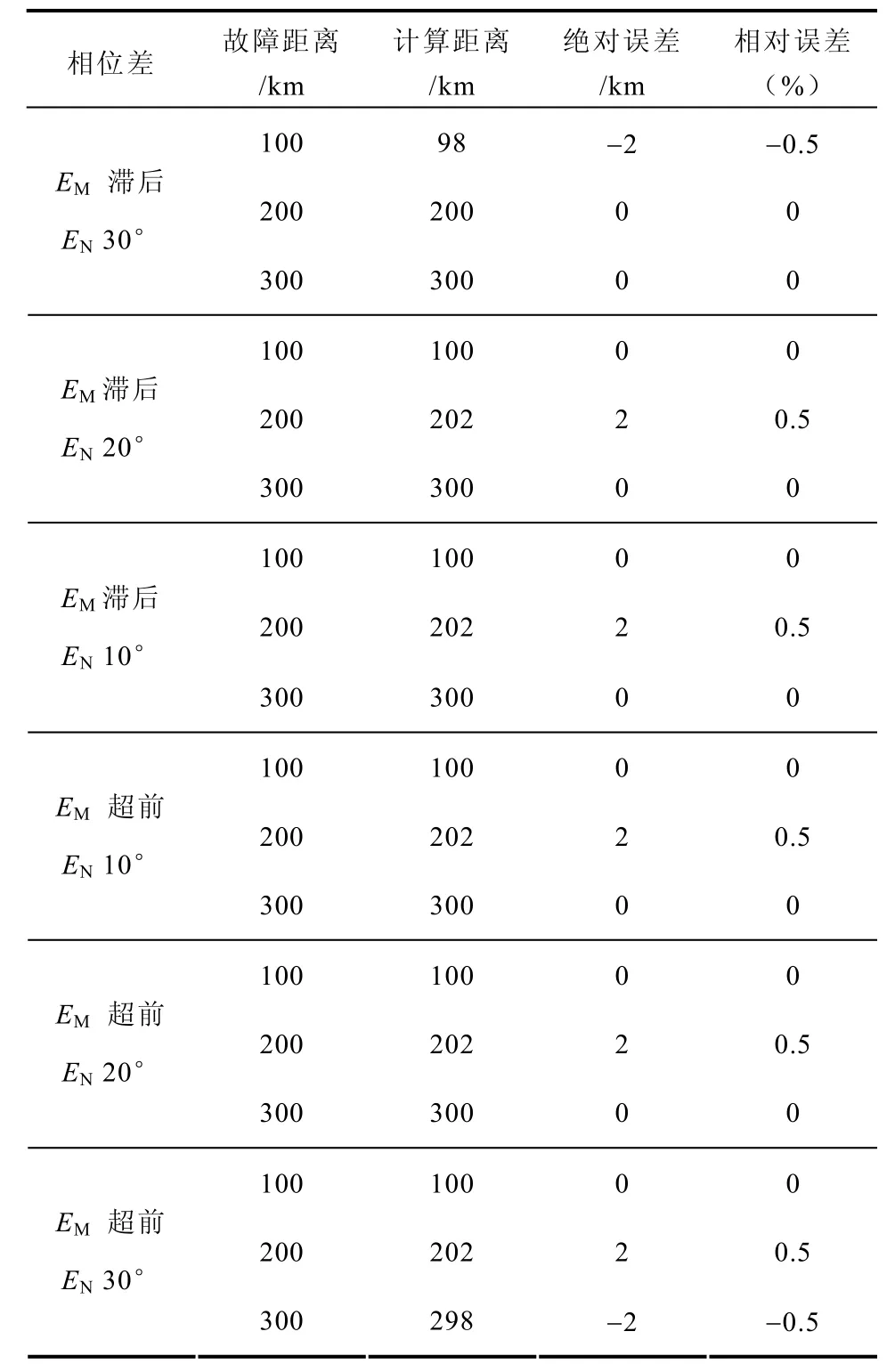
表3 不同负载情况的测距结果Tab.3 Location results under different load conditions

2.5 系统阻抗的影响

为验证在弱系统侧（系统阻抗大）本方法的测距精度，改变ZM1和ZM0的幅值和阻抗角，使其远小于N端系统的阻抗值，并使两侧系统阻抗角具有较大差别，过渡电阻为50 Ω，N侧的测距结果见表 4。

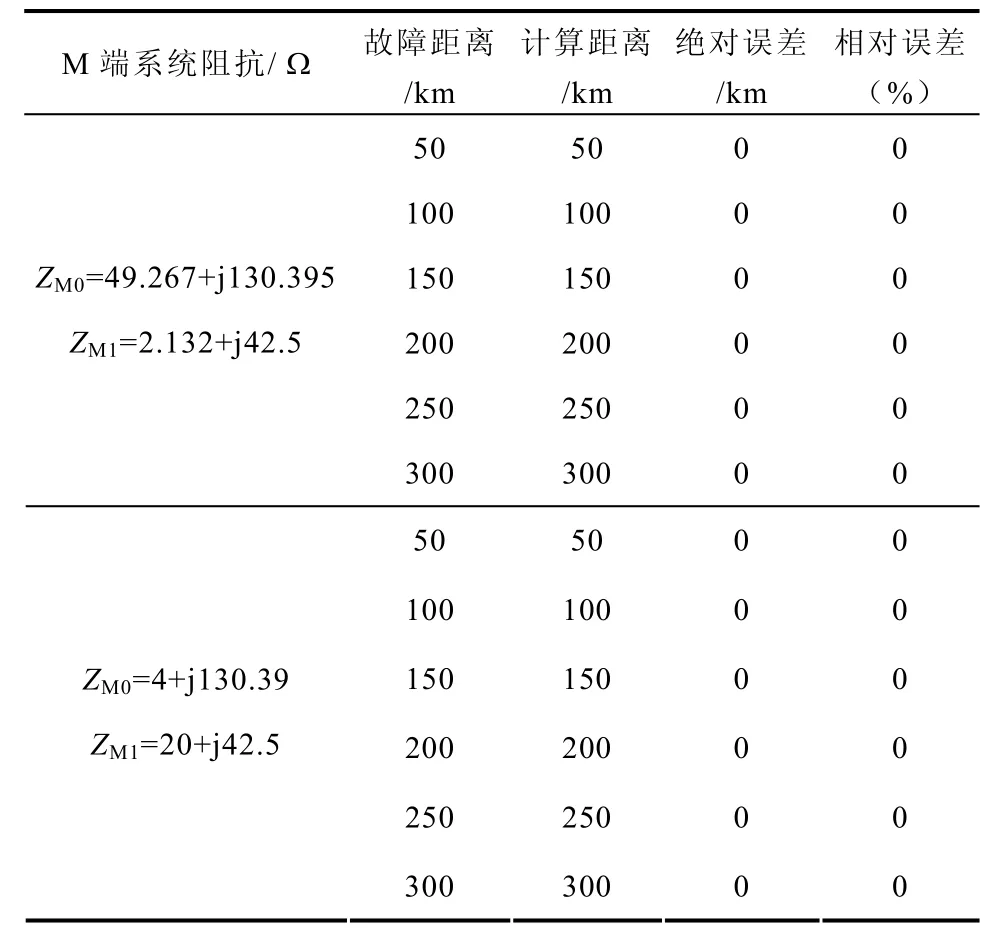
表4 不同系统阻抗的测距结果Tab.4 Location results under different system impedances

由表4可见，本文算法不受系统阻抗的影响，在弱系统侧仍然能够有很高测距精度。而基于故障支路电流相位估测（无论是零序还是负序）的单端测距方法，在上述情况下测距结果均存在很大误差。

2.6 系统阻抗和电动势精确计算值

将计算所得的故障距离和过渡电阻值代入式（7）～式（10），通过求解式（5）、式（6）和式（11）即可得到对端系统电动势和阻抗值。在系统参数与2.5节相同的情况下，表5列出了M端系统电动势和阻抗的测量结果（N端为测量端）。

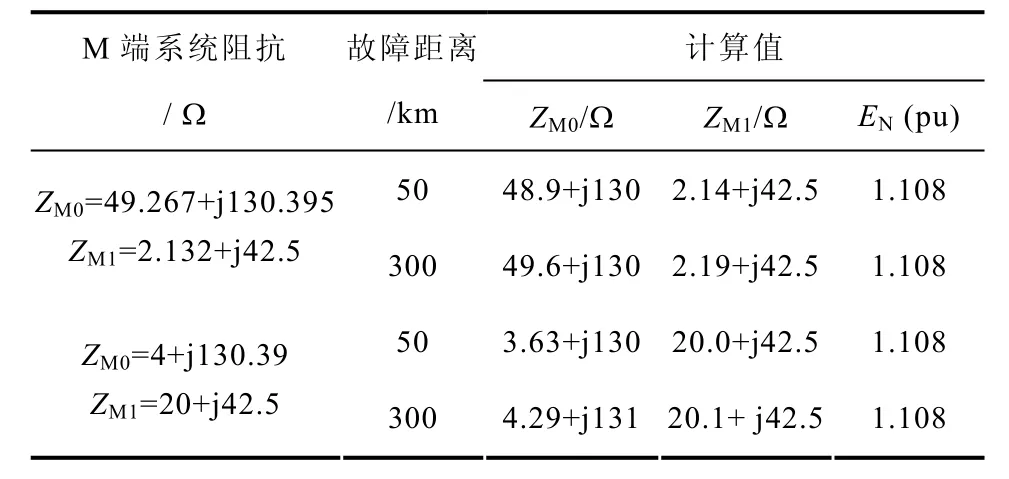
表5 对端系统电动势和阻抗的计算结果Tab.5 Results of electric potential and impedances of the opposite system

由表5可见，本文方法对对端系统电动势和阻抗的计算同样具有非常高的精度。

2.7 对比分析

为验证算法性能，下面将本文算法与文献[12]方法进行对比分析。所采用仿真模型与文献[12]中第 4节一致。故障算例与文献[12]中表 4一致。两种方法的测距误差见表6。

表6 测距性能对比Tab.6 Performance comparison

由表 6可见，对于文献[12]中的算例，本文方法的测距误差在一个计算步长之内，精度远高于文献[12]中所述的采用RL线路模型的近似方法。

3 结论

（1）本文推导了基于分布参数的输电线路发生单相接地故障时，首末端电压电流关系表达式。

（2）提出了利用单相跳闸后信息的分布参数输电线路单相接地故障单端精确测距方法。

（3）基于大量的仿真结果，验证了本文所提方法对不同故障距离、不同过渡电阻、不同负载情况以及不同系统阻抗条件下均具有很高的测距精度。

本文仅针对永久性故障进行了讨论，对于瞬时性故障以及理想金属性接地故障，仅需修改跳闸后阶段的系统方程，相关内容将在后续工作中体现。

附录 线路首末端电压电流关系推导

附图1 单相接地故障系统图App.Fig.1 Single-line-to-ground fault in a transmission system

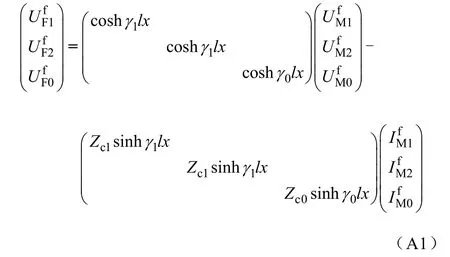
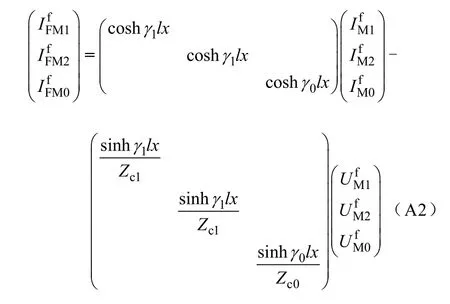
在故障点的边界条件可以表示为

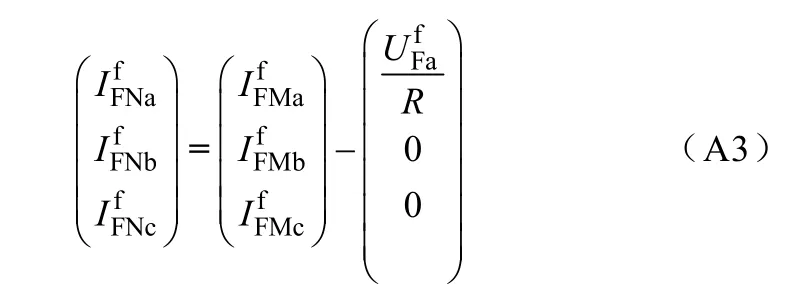
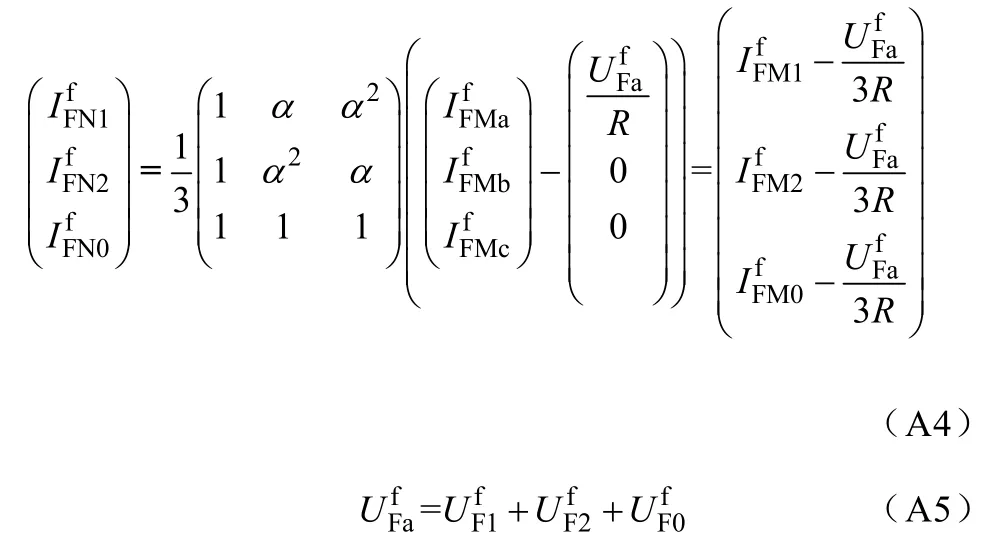
由式（A1）～式（A5）可得

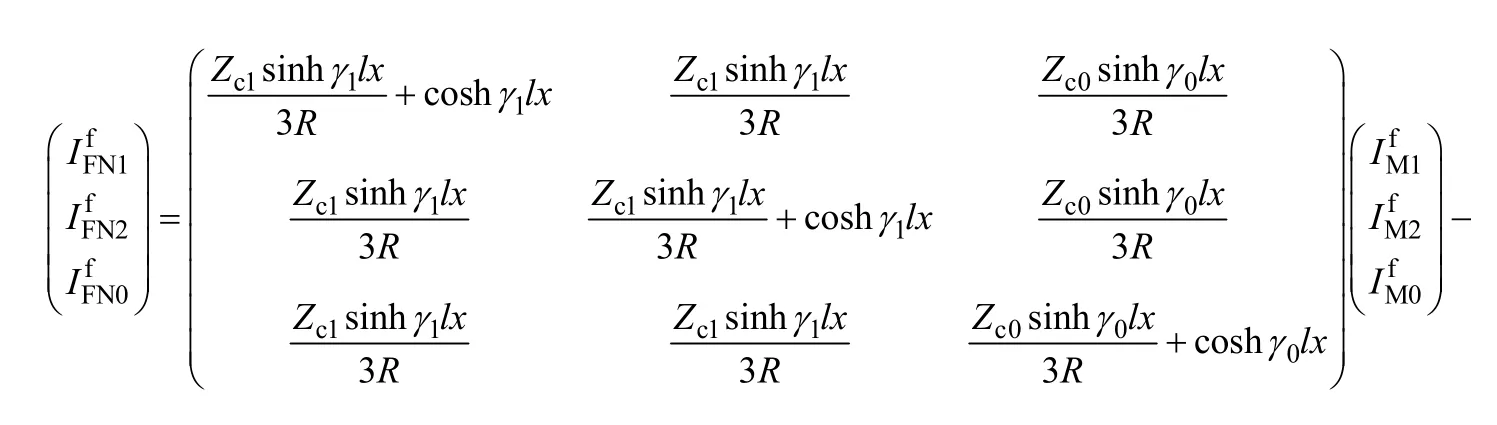
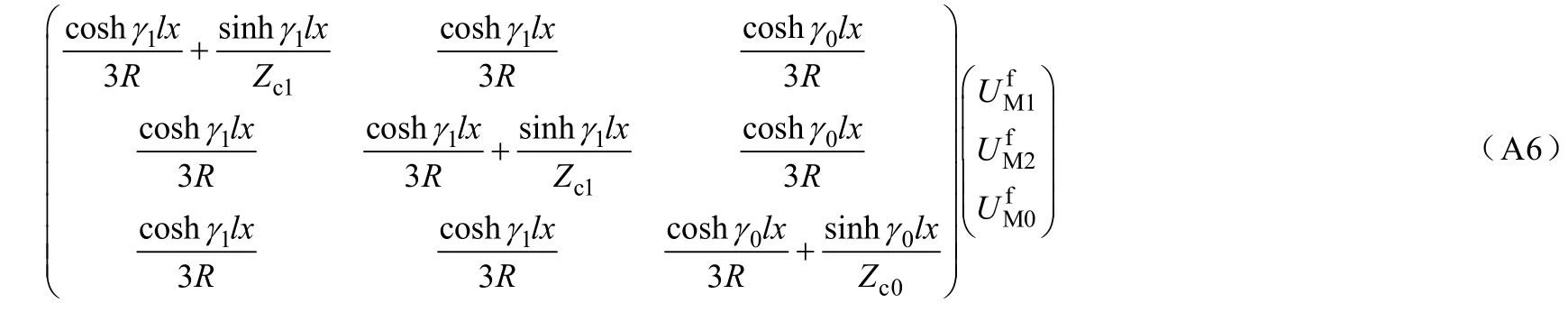
故障点和N端的电压电流关系同样满足线路的传输方程，如式（A7）和式（A8）所示：

将式（A1）、式（A6）代入式（A7）、式（A8）即可得到式（5）、式（6）及A、B、C、D。

[1] Takagi T,Yamakoshi Y,Yamaura,M,et al.Development of a new type fault locator using the one-terminal voltage and current data[J].IEEE Transactions on Power Apparatus Systems,1981,PAS-101(8):2892-2898.

[2] 葛耀中.新型继电保护与故障测距原理与技术[M].西安:西安交通大学出版社,1996.

[3] Johns A T,Jamali S.Accurate fault location technique for power transmission lines[J].IEE Proceedings C Generation Transmission & Distribution,1990,137(6):395-402.

[4] Kezunovic M,Perunicic B.Automated transmission line fault analysis using synchronized sampling at two ends[C].1995 IEEE Power Industry Computer Application Conference,1995:407-413 .

[5] 董新洲.小波理论应用于输电线路行波故障测距研究[D].西安:西安交通大学,1996.

[6] 胡帆,刘沛,程时杰.高压输电线路故障测距算法仿真研究[J].中国电机工程学报,1995,15(1):67-72.

Hu Fan,Liu Pei,Cheng Shijie.Investigation of the high voltage transmission line fault location by digital simulation[J].Proceedings of the CSEE,1995,15(1):67-72.

[7] 张哲,陈德树.高压输电线路故障测距中的伪根问题及其改进方法[J].中国电机工程学报,1992,12(6):11-17.

Zhang Zhe,Chen Deshu.False root and its modifycation for fault locating on electric power transmission lines[J].Proceedings of the CSEE,1992,12(6):11-17.

[8] 蔡德礼.高压输电线路故障点定位的一种新的计算机方法[J].重庆大学学报:自然科学版,1982,6(2):1-17.

[9] 李志民,陈学允.基于单侧信息的输电线路故障测距新方法[J].中国电机工程学报,1997,17(6):416-420.

Li Zhimin,Chen Xueyun.A novel algorithm for power transmission line fault location using the oneterminal current data[J].Proceedings of the CSEE,1997,17(6):416-420.

[10] 王宾,董新洲,薄志谦,等.特高压长线路单端阻抗法单相接地故障测距[J].电力系统自动化,2008,32(14):25-29.

Wang Bin,Dong Xinzhou,Bo Zhiqian,et al.An impedance fault location algorithm for UHV long transmission lines with single-line-to-ground faults[J].Automation of Electric Power Systems,2008,32(14):25-29.

[11] Haun R K.13 years' experience with single-Phase reclosing at 345 kV[J].IEEE Transactions on Power Apparatus Systems,1978,PAS-97(2):520-528.

[12] 杨铖,索南加乐,李亚利.基于 R-L模型的单相重合闸线路故障测距方法[J].电力系统自动化,2010,34(10):71-74.

Yang Cheng,Suonan Jiale,Li Yali.Study on the fault location algorithm based on R-L model for transmission lines with single-pole reclosure [J].Automation of Electric Power Systems,2010,34(10):71-74.

[13] 邱关源,罗先觉.电路[M].5版.北京:高等教育出版社,2006.