三种绝缘气体下开关设备的温度场及流场对比与分析

张俊民 高荟凯 冯 昊

（北京航空航天大学自动化科学与电气工程学院 北京 100191）

1 引言

密封式中压开关设备不仅具有较高的运行可靠性，而且还在减小占地面积、节约土地资源方面占有优势，故近年来逐渐受到关注。SF6气体是一种性能优良的绝缘气体，已被广泛地应用于开关设备中。然而 SF6气体是一种温室气体，对全球温室效应有一定的影响，因此在开关设备的设计中减少、限制甚至禁止 SF6气体的使用，逐渐成为开关设备发展的趋势[1]。空气是最常见的绝缘气体，N2也是廉价和环保的气体，开始逐渐受到关注和使用。因此将空气、N2作为SF6气体的替代气体应用于开关设备中，具有较大的研究意义。近年来国内外学者对寻求 SF6气体替代气体进行了大量的研究。文献[2,3]从N2和N2与SF6混合气体的击穿特性的角度，来讨论将 N2和 N2与 SF6混合气体作为替代气体的可行性，认为SF6/N2混合气体具有较好的绝缘特性，替代可行。文献[4]从绝缘水平角度，讨论将 N2或C4F8作为 SF6气体的替代气体有哪些优点和缺点。虽然N2容易获得，且其为最环保气体之一，但绝缘能力较SF6低。C4F8在均匀电场中的绝缘强度为SF6气体的1.18～1.25倍左右，但其仍为温室气体，且价格昂贵。文献[5]从开断性能、燃弧特性、电弧温度形态的角度，讨论了空气、CO2、N2等气体对SF6气体的可替代性；文献[6]中介绍了一种用含碳气体与O2的混合气代替SF6作为GIS用绝缘气的技术，但是在电弧中能生成CO和O3。这些文献都对寻求SF6气体替代气体提出了宝贵的指导意见。

温升是影响开关设备安全性能的重要指标，温升过高直接影响开关设备的安全稳定性。因此要寻求替代 SF6气体的环保气体，开关设备中元件在替代气体里的温升是分析其可行性的重要参数之一。但国内外从温升的角度讨论替代气体的可行性的文章非常少，目前为止尚未见到关于 SF6气体和替代气体对开关设备温升影响对比分析的公开文献报道。

封闭条件下载流回路的发热和散热是研究温升的关键之一。开关设备的发热源于零件的焦耳热损耗，考虑到集肤、邻近和涡流效应，如果直接计算会带来很大误差；而散热也是集传导、对流和辐射等传热方式耦合的复杂物理过程，故发热与散热过程可采用数学建模和数值计算方法来研究。在数值计算中，需要对电磁场、温度场与气流场进行耦合求解。由于开关设备的三维模型较为复杂，数值分析过程中网格剖分数目多，从而给开关设备温度场的数值计算带来较高的难度。

本文以某型号开关设备为研究对象，首先根据电磁场理论，利用棱边单元法计算了初始温度下载流导体和外壳的焦耳损耗（含集肤效应的影响和涡流损耗）。然后基于热传导微分方程、流体运动控制方程及辐射换热方程，建立了开关设备内部传导、对流和辐射换热的耦合传热数学模型，并采用壁函数方法处理边界对流换热问题。采用有限容积法对方程进行离散，求解开关设备分别在 SF6、N2、空气中温度场和气流场，得到开关设备在这三种气体中的三维温度场与气流场的分布，并对计算结果进行对比与分析。

2 数学模型

在开关设备内，载流导体的电阻损耗，外壳的涡流损耗以及接触电阻损耗是热量产生的主要来源；而其散热则通过传导、对流和辐射这三种形式进行。载流导体上各元件及与之相连的各固体元件间主要以传导方式传热，温度升高的各元件又通过自然对流换热和热辐射两种方式将热传递到周围环境，然后经外壳传到开关设备的周围空气中。

2.1 焦耳热损耗数学模型

在开关设备涡流损耗的数值分析中，采用磁矢量位A来进行计算。当主导体回路通额定交流电流时，其控制方程如下[7]：

式中μ——磁导率；

J——总电流密度矢量；

Js——源电流密度矢量；

Je——涡流密度矢量；

σe——材料电导率；

忽略位移电流的影响。

焦耳热损耗包括主回路中的电流（考虑集肤效应和邻近效应）及外壳中的感应涡电流产生的损耗。这些损耗使用有限元方法计算，受主回路电流、材料特性、导体尺寸和温度的共同影响。20℃时，主导体和外壳的单位体积焦耳热损耗表达式如下[7]：

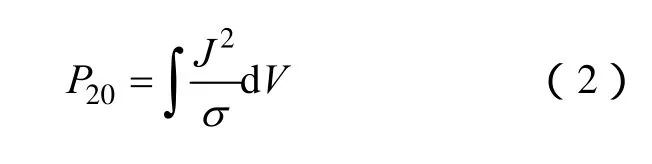
在主回路导体中，可以忽略Je，即Js与J相等，所以当温度升高时，随着电阻率的线性增大，焦耳热损耗也近似线性的增大。温度为T（T＞20℃），主回路导体焦耳热损耗表达式如下：

式中α——电阻温度系数。

在外壳中，J=Je，Js=0。固定频率下，涡流损耗与电阻率成反比[8]，故外壳焦耳热损耗表达式如下：

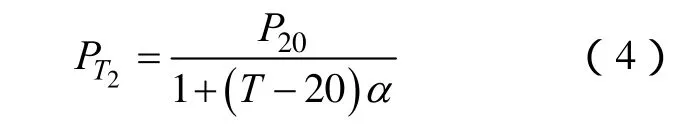
接触电阻焦耳热损耗表达式如下：

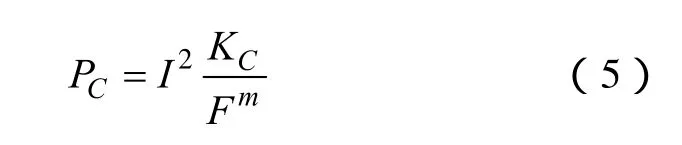
式中I——额定电流；

F—— 接触压力，由厂家给出；

m—— 与接触形式有关的系数（对点、线、面接触，其值分别为0.5、0.7、和1）；

KC—— 与接触材料、表面状态、接触形式等有关的物理量。

以上所计算的三种焦耳热损耗均会被作为热源加入到温度场与气流场的计算中，实现电磁场与气流场的耦合。

2.2 温度场与气流场数学模型

开关设备内散热涉及传导、对流和辐射等传热方式。封闭开关设备内零件众多，气体流动状况复杂，可采用标准k-ε湍流模型对传热和散热进行描述[9]。控制方程包括质量、动量、能量守恒方程以及k方程和ε方程，求解的变量包括速度、温度、湍流脉动动能k和脉动动能耗散率ε等。变量的控制方程可以写成统一的形式，其通用控制方程如下[10]：

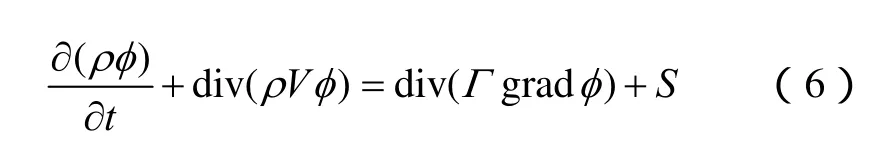
式中ρ——密度；

φ—— 温度、速度和压强的通用变量；

V—— 速度矢量；

Γ—— 扩散系数；

S—— 源项，其中包括了焦耳热损耗Φ1及辐射散热量Φ2。

Φ1即为上一小节所述的焦耳热损耗，包括：载流回路损耗，外壳损耗和接触电阻损耗。

由于发热体表面与周围环境气体存在温度差，因此两者之间存在辐射换热。两者的辐射换热量为

式中σ——斯特潘·玻尔兹曼常数，其值为5.67×10-8W/(m2·K4)；

ξ—— 发热体热源辐射度，计算中取常数；

A—— 热源表面积；

Th——发热体表面温度；

Ta——周围环境气体温度。

这里辐射换热包括了载流导体与柜体以及柜体向外围空气的辐射。

主回路与周围气体的对流传热计算中采用了标准k-ε湍流模型并将壁函数[11]作为气固界面的边界条件。壁函数法的使用避免了在k-ε模型计算壁面传热中的网格加密问题，大大节省了计算机的运行时间和存储空间[12,13]，同时，也避免了在计算对流传热系数中对壁面温度反复迭代求解的过程[14]。

壁函数法在计算壁面与气体的对流换热时，引入了变量无量纲速度u+、距离y+和温度T+，其计算方法如下：

壁函数法假设与壁面相邻的第一个节点是布置在旺盛的湍流区域内，此区域的速度u+与温度T+的分布服从相应的对数分布律，即用公式将壁面物理量与湍流核心区的相应物理量联系起来。壁面上的切应力τW与热流密度qW即按第一个近壁节点与壁面上的速度与温度之差来计算，其公式如下：

求解式（8）～式（12），可以求出热流密度qW，从而得到湍流粘性系数ηt和湍流导热系数λt的表达式如下：

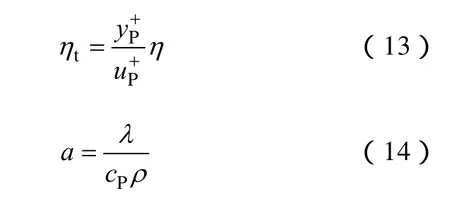
式（8）～式（14）中qW——壁面热流密度；

TW,uW——壁面上的温度与速度；

TP,uP—— 近壁节点P的温度与速度；—— 无量纲距离、速度和温度；

σL—— 分子普朗特数；

ρ—— 流体密度；

cP—— 流体定压比热容；

cμ—— 经验常数；

λ—— 流体热导率；

v—— 流体运动粘度；

η—— 流体粘性系数。

3 仿真计算

3.1 开关设备模型

本文以某型号开关设备为模型，来研究 SF6、N2、空气对开关设备内温度场及气流场的影响。该开关设备为圆筒式户外型气体绝缘金属封闭开关设备。其内部的主要设备包括母线、断路器、电压、电流互感器、三工位隔离开关等。该开关设备三相为分筒式结构，每相构造相同，外壳由铝制及钢制圆筒和绝缘套环组成。开关设备的额定电压40.5kV，额定电流2 000A，额定频率50Hz。

由于该开关设备三相构造相同，因此在计算分析中取其中一相即可。所建开关设备模型及载流回路元件分布如图1所示。导电外壳包括四通套筒1、2、3，二通套筒，母线套管等组成，如图1a中所示；载流回路包括导电杆，触指，导电带，导电板，动导电杆，静导电杆，外接母线等，如图1b所示。计算域边界设置成环境温度。计算时，坐标原点取在开关设备接线板的顶点，见图1左下角处。

图1 开关设备几何模型Fig.1 The model of switchgear

3.2 参数设置与初始条件

由汤逊理论[15]可知，增大气体压力能较大程度的提高开关设备内气体的绝缘能力。N2和空气的绝缘能力均低于SF6，约为SF6气体的1/3。因此，在保证三种气体绝缘能力相当，且气压较低的前提下，分别设计空气和 N2的初始压力值为 0.25MPa，SF6的初始压力值为0.08Mpa。三种气体的初始温度T0均为20℃。数值计算中涉及到三种气体的热力学参数包括密度、粘度、比热、热导率和热膨胀系数等，其值可参见文献[16]。

开关设备内载流回路的零件材质主要为纯铜，绝缘套管为环氧树脂，外壳主要为铝材，少数钢材。各材料物理参数详见参考文献[16,17]。

利用棱边单元法，计算出工频额定电流下载流回路及外壳的功率损耗，本文不再详细赘述其具体过程。这些功率损耗都作为热源加入温度场的计算，并考虑功率损耗随温度的变化而改变。

图1中主要零部件在额定电流下，20℃时的功率损耗见表1。

表1 主要零件功率值（20℃）Tab.1 Power loss of components（20℃）

3.3 网格剖分

本文所计算的开关设备模型复杂，零件数目多，每一相有138个零件，且形状多不规则，因此网格的剖分难度比较大。计算中采用直角坐标系和六面体网格剖分，计算域内六面体网格数目为120万左右。网格剖分如图2所示。

图2 网格剖分Fig.2 The mesh of numerical calculation

3.4 计算结果与分析

3.4.1温度场

三种气体下的开关设备温度分布如图3所示。

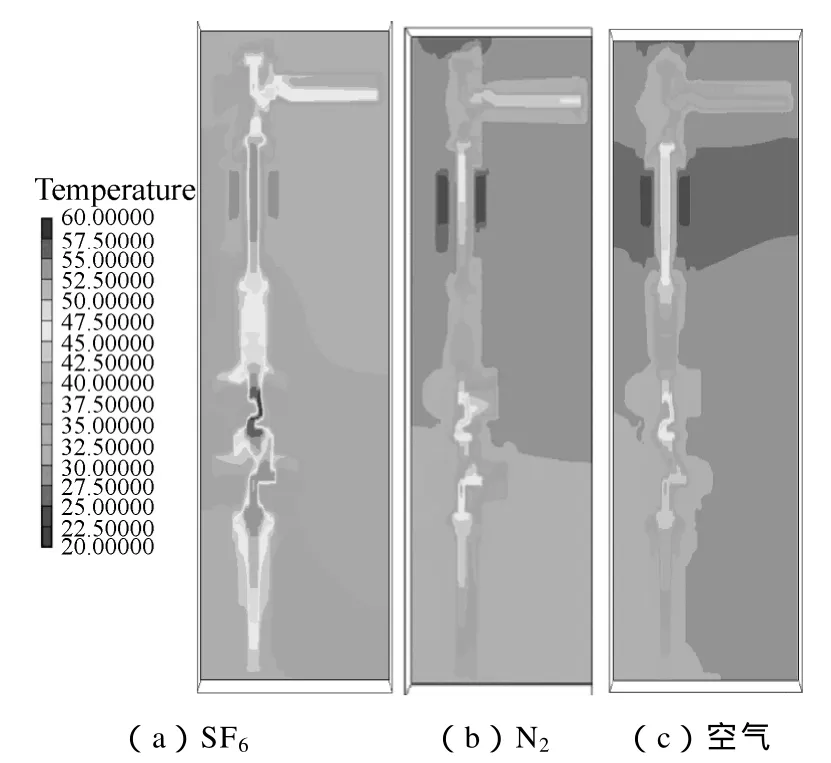
图3 三种气体下开关设备温度分布Fig.3 Temperature field of switchgear in three gases

从图3可以看出，温度最高部分均集中在导电带和上导电杆处。造成温度高低差异的主要原因有元件电阻值的大小不等、各元件的体积大小不同以及周围气流流动情况。电阻值较高而体积较小的元件，温度就会偏高。如图中导电带部分，电阻较高，同时导体尺寸较小，则温度较高。同时温度偏高的元件也会将热量传给与其相邻的元件，所以使得回路中与其相连的元件温度值也较高。计算结果显示，载流回路在 N2和空气中的温度低于在 SF6的温度。

3.4.2三种气体中温升对比分析

读取各元件温度值，将三种气体环境下载流回路的温度绘制成曲线，如图4所示。图中的横坐标为零件编号，即将载流回路上元件按图1所示顺序从左到右的依次编号；纵坐标为载流回路元件的温度的与初始温度T0的比值。

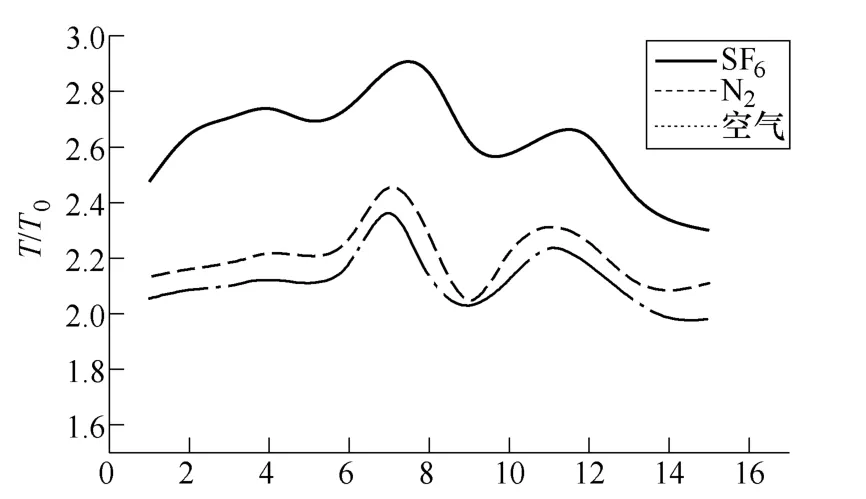
图4 三种气体环境下载流回路温度Fig.4 The temperature of current carrying conductor in three gases

由图4可以看出，三种气体环境下开关设备载流回路的温度分布基本一致，但在 SF6气体中的温升最高，而N2和空气中的温升比较接近。

如果载流导体产生的热量传递到气体内是相同的，则决定气体散热能力的参数主要为热扩散系数。热扩散系数越大，气体导热能力越好；相反，热扩散系数越小，气体导热能力越差。热扩散系数α与热导率λ、气体比热容cP、气体密度ρ有关，即a=λ/(cPρ)，由此可计算出三种气体的热扩散系数大小关系为：a空气＞aN2＞aSF6，且 N2的热扩散系数略高于空气的。

所以，在三种气体条件下，当开关设备中绝缘气体导热能力较差，即热扩散系数较小时，载流回路传递到气体中的热量不能较快地在气体中扩散，进而也不能及时通过外壳传到周围空气中，故与导热能力好—热扩散系数较大的气体相比，其载流回路的温升相对较高。因此，当其他条件相同时，气体的热扩散系数越小，载流回路的温升越高；热扩散系数越大，气体中导电回路温升越低。故 SF6中载流回路温升高于N2和空气中载流回路的温升。从温升角度来看，开关柜中有可能用 N2或空气作为SF6的替代气体。

3.4.3气流场

SF6气体中开关设备的气流场如图 5所示，在N2和空气中的气流场与SF6气体中的基本相同，因此不再赘述。

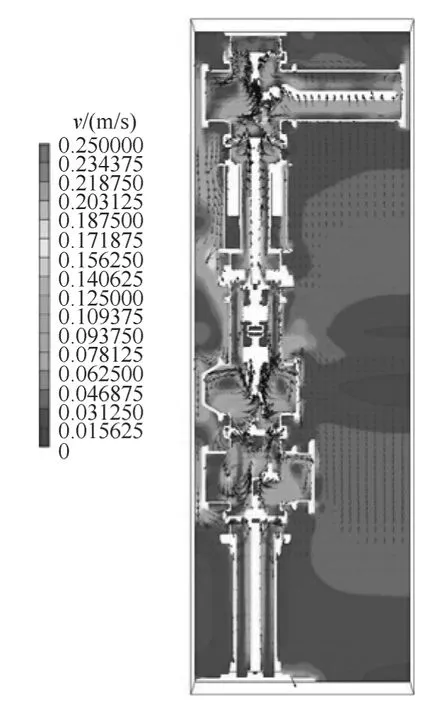
图5 SF6气体环境下流场Fig.5 Fluid field in the switchgear filled with SF6

图5中的速度矢量箭头大小和颜色尺度分别明显出计算区域内气体的流动方向及流速大小。

由于载流回路不断散发热量，使其周围气体温度升高，温度较高的气体将上升。影响开关设备中气流流速快慢的主要因素有开关设备内部结构，换热表面的形状，元件表面与流体之间的温差。开关设备内气流通道截面小，此处的流速就高。元件表面温度高，附近气流受热较快，流速也就高。从图中可以看出，开关内部内有气孔处，及导电带、导电杆等温度高处气流流速快。由于该开关设备结构为细长圆柱形，气流通道长而窄，故气流速度较低。

3.4.4气流场分布比较

三种气体环境下流速分布规律基本一致，但流速大小略有差别，其中 SF6气体的流速高于 N2和空气的，N2的流速与空气的接近。图6所示的三种气体中载流回路导电带处气流场，可以反映出这一差别。

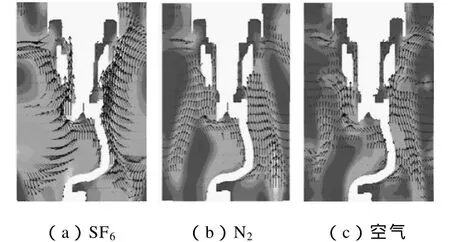
图6 三种气体中导电带处气流场Fig.6 Fluid field around conductive band in three gases

当开关设备结构相同时，影响气体流速快慢的主要因素是流体的粘度和元件表面温度。流体的粘度越小，流动过程中气流所受阻力也越小，因此流速越快；相反，粘度越大，气流流速越慢。元件表面温度越高，气流流过时受热越快，因此流速也越快。三种气体比较：SF6粘度最小，N2粘度稍小于空气；并且由3.4.1中已知，载流回路的温度在SF6中最高，N2中温度与空气中温度接近。因此，这两个因素的影响，使得三种气体中，SF6气流流速快，N2气流流速与空气流差别不大。然而，尽管SF6气体中的流速高于其他两种气体，但由于在开关柜中为自然循环对流，其未能够使温升降低到N2和空气中的温升。

4 结论

（1）计算出了载流导体和外壳在工频和额定状况下的焦耳热损耗；确立了传导、对流和辐射耦合传热的数学模型，并采取壁函数处理固体与流体界面的对流换热问题，并在此基础上对开关设备三维温度场和气流场进行了数值计算与分析。

（2）模拟了开关设备三维温度场和气流场，分别得出了在 SF6、N2、空气中开关设备内温度场和气流场的分布，结果表明三种气体环境下开关设备的温度分布基本一致，温升大小为 SF6内最高，氮气内与空气内的近似相等。载流回路最高温度处均集中于导电带和导电杆处。三者的流速分布大体分布相同，流速大小为 SF6中气体流速快，氮气流速与空气流速相近。

（3）通过比较开关设备中三种气体的温度场和气流场分布，在满足绝缘条件前提下，从温升方面考虑，由于空气、氮气中温升低于SF6气体内温升，因此使用空气、氮气作为SF6气体的替代气体是可行的。

[1] 徐建源, 任春为, 司秉娥, 等. 40.5kV SF6充气式开关柜三维电场分析[J]. 中国电机工程学报, 2008,28(15): 136-140.

Xu Jianyuan, Ren Chunwei, Si Binge, et al. Three dimensional electric field analysis of 40.5kV SF6cubicle gas-insulated metal-enclosed switchgear[J]. Proceedings of the CSEE, 2008, 28(15): 136-140.

[2] 李慧芬. SF6气体替代面临的诸多挑战[J]. 高电压技术, 2000, 26(3): 50-51.

Li huifen. Many challenges to substitution for SF6[J].High Voltage Engineering, 2000, 26(3): 50-51.

[3] 孙鹏程, 王帮田, 洪文芳, 等. SF6/N2混合气体绝缘特性的实验研究[J]. 中国电力, 2012, 45(12): 71-75.

Sun Pengcheng, Wang Bangtian, Hong Wenfang, et al.Experimental studies on electrical insulation performances of SF6/N2gas mixtures[J]. Electric Power,2012, 45(12): 71-75.

[4] 张强华, 谭燕, 邬建刚. 40.5kV无SF6C-GIS开关柜研究[J]. 高压电器, 2011, 47(6): 29-38.

Zhang Qianghua, Tan Yan, Wu Jiangang. Research of 40.5kV non SF6C-GIS[J]. High Voltage Apparatus,2011, 47(6): 29-38.

[5] 贾申利, 赵虎, 李兴文, 等. SF6替代气体灭弧性能的研究进展综述[J]. 高压电器, 2011, 47(11): 87-97.

Jia Shenli, Zhao Hu, LI Xingwen, et al. Survey of recent researches on the arc quenching characteristics of SF6substitute gases[J]. High Voltage Apparatus,2011, 47(11): 87-97.

[6] Uchii T. Gas in sulated switch gear: US, 0221626[P].2007-09-27.

[7] Joong Kyoung Kim. A novel coupled magneto-thermalflow analysis for temperature rise prediction of power apparatus[J]. Electrical Machines and Systems, 2008(43):585-588.

[8] 雷银照. 电磁场[M]. 北京: 高等教育出版社, 2008.

[9] 张俊民, 侯振华, 张春朋, 等. 27.5kV GIS母线室三维温度场的数值计算[J]. 电工技术学报, 2011,26(12): 62-67.

Zhang Junmin, Hou Zhenhua, Zhang Chunpeng, et al.Three dimensional thermal field numerical calculation of 27.5kV gas-insulated switchgear bus bar’s cabinet[J]. Transactions of China Electrotechnical Society,2011, 26(12): 62-67.

[10] 陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2001.

[11] Kim S W. Coupled finite-element-analytic technique for prediction of temperature rise in power apparatus[J]. IEEE Transactions on Magnetic, 2002, 38: 921-924.

[12] Chico X Albets. Analysis of wall-function approaches using two equation turbulence models[J]. International Journal of Heat and Mass Transfer, 2008, 51: 4940-4957.

[13] Barakos G. Natural convection flow in a square cavity revisited: laminar and turbulent models with wall functions[J]. International Journal for Nmerical Methods in Fluids, 1994, 18: 695-719.

[14] Ho S L, Li Y. A 3-D study of eddy current field and temperature rises in a compact bus duct system[J].IEEE Transactions on Magnetics, 2006, 42(4): 987-990.

[15] 王胜辉. 高电压绝缘技术[M]. 北京: 华北电力大学出版社, 2002.

[16] 刘光启. 化学化工物性数据手册[M]. 北京: 化学工业出版社, 2002.

[17] 方昆凡. 工程材料手册[M]. 北京: 北京出版社,2002.