基于切换模型的双向AC-DC变换器控制策略

田崇翼 李 珂 张承慧 庄飞飞 叶保森

（山东大学控制科学与工程学院 济南 250061）

0 引言

在能源需求和环境保护的双重压力下，分布式发电技术获得了越来越多的重视和应用，微电网技术作为分布式电源和电网连接的桥梁和缓冲也成为当前的研究热点[1,2]。目前常用的微网结构有交流微网、直流微网和交直流混合微网[3-6]。

在交直流混合微电网中，通常需要双向AC-DC变换器作为能量接口单元，控制直流和交流母线功率流动，以保证微网功率平衡、维持母线电压稳定并提高系统电能质量。目前多数研究交直流混合微电网的控制文献都采用小信号建模方法来分析双向AD-DC变换器[7-9]，基于状态空间平均的小信号法简单易用，便于稳定性分析以及控制器的设计。然而，交直流微网中含有大量波动性很强的微源，双向 AC-DC变换器工作点需要大范围的突变。小信号平均模型是通过忽略模型中高次项而近似得到，这种近似得到变换器小信号模型的建模方法存在大信号扰动时，系统可能出现不稳定、建模精度不高等诸多问题[10]。近年来，混杂系统理论和应用的不断进步为电力电子系统建模和控制提供了一种新的工具。文献[11]给出了切换线性自治系统稳定控制条件，提出通过设计切换序列使系统状态趋近于一个稳定切换平衡点。文献[12]进一步研究线性切换系统稳定切换律的设计问题，并以三种典型的DC-DC变换器进行了实际控制。文献[13]以双向DC-DC变换器为例研究了切换系统的能控性和能观性，文献[14]基于切换理论研究了三相PWM整流器在周期性切换律下的稳定性问题。文献[15,16]研究了切换模型下的APF控制并取得很好的效果。文献[17]探讨了基于切换理论下开关变换器统一建模问题。采用电力电子混杂系统建模可以直接对系统大信号过程建模，不存在任何近似，得到模型较为精确，因此更能真实反映电力电子系统的实际物理工作过程。

本文基于切换系统理论，首先建立双向AC-DC切换动态模型，然后采用储能函数作为系统Lyapunov函数，以系统能量衰减最快为目标设计了最优切换控制策略。同时为了便于控制器数字化实现，建立了切换系统单步预测模型并对控制策略进行离散化处理。由于直接对系统大信号过程进行建模，本文所得到的模型比较精确，增强了双向AC-DC变换器抗大范围扰动的能力。相对于传统的SVPWM调制方法，该算法无需进行矢量计算，对复杂电路的建模和分析更方便。本文最后进行了仿真模拟并搭建了实验平台，仿真和实验结果表明所采用的建模方法和控制策略有效。

1 双向AC-DC变换器切换系统模型

1.1 切换系统理论基础

切换系统是一类重要的混杂系统[18]，它是由几个连续时间子系统或离散时间子系统及作用在其中的切换规则构成的统一动态系统。在切换过程中，每一时刻系统的状态只符合其中1个子系统的规律。通过在多个子系统之间进行适当切换，以实现一定的性能要求。切换信号可根据时间、状态或由更复杂的方式产生。一般切换系统模型可以表示为

式中，σ(t,x)∶[0,∞]→{1, 2, …,m}为分段常值函数，右连续，称为系统切换信号，对于由开关管组成的电力电子电路来说，m=2l，l为开关管对数。σ=k时表示系统处于第k个子系统。x为系统的状态变量；u为系统输入。电力电子电路中，每一种开关组合分别对应一种电路拓扑，由此可以得到相应子系统的连续状态方程，不同开关组合的变化可以看作是离散事件，因此可以把变换器的实际工作过程描述为在特定切换规则的控制下不同连续子系统之间的切换。

1.2 双向AC-DC切换建模

双向AC-DC结构如图1所示，其中，Ea、Eb、Ec为交流侧三相电压；ia、ib、ic为交流侧三相电流；Udc为直流侧电压。R、L分别为滤波电抗器的电阻和电感；Ura、Urb、Urc为输入整流器的三相离散电压信号；C为滤波电容；kp(p=a, b, c) 表征开关器件状态，定义kp=1表示第p对开关上桥壁开通，下桥壁关断，k=0表示下桥壁开通，上桥壁关断。

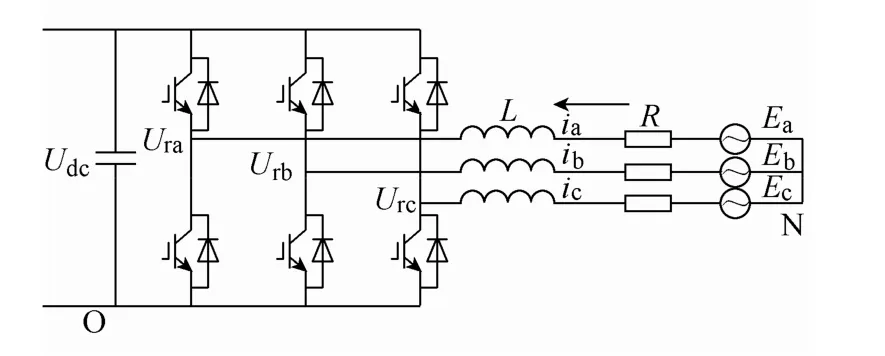
图1 双向AC-DC变换器结构图Fig.1 Principle of AC-DC converter

根据基尔霍夫电压定律，可以求出双向AC-DC变换器电流电压动态方程

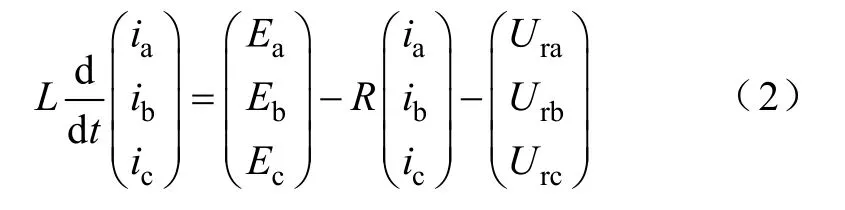
式中

双向AC-DC变换器正常工作过程中，ka、kb、kc共对应8种有效开关组合，即:000、001、010、011、100、101、110、111。其中000和111组合作用相同，因此定义7种有效的切换模态，即σ(x)∈{1,2, ··, 7}，则系统开关函数可以表示为

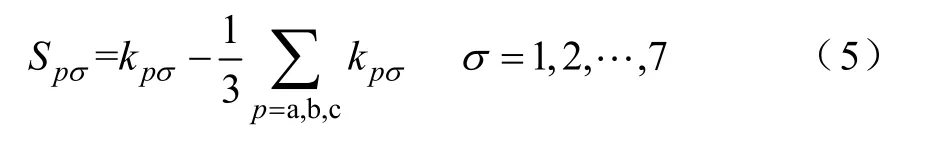
式中，pSσ表示第p对开关在切换到σ模式时的值，引入状态变量x=(ia, ib, ic)T，针对每一种开关组合，可以得到一种电路拓扑和相应的状态方程。假定三相交流电压对称，并忽略三相交流线路电阻电感的不对称性，得到双向AD-DC变换器切换模型为

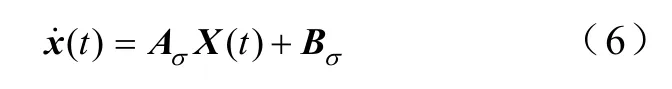
其中

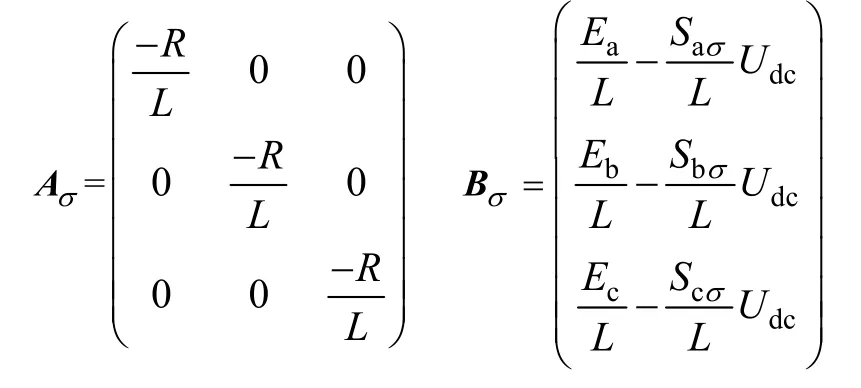
2 最优切换路径设计

双向AC-DC的电流跟踪控制目标是使得系统状态满足x(t)=x*,x*为外部给定的参考值，可以视为系统的切换平衡点。由式（6）可知，通过控制σ(x)选择不同值，就可以得到对应的电力电子器件驱动信号，从而使得AC-DC变换器切换到不同的状态方程。因此需要设计系统的最优切换规则，从而在保证系统全局稳定的前提下，控制状态变量的运动轨迹使之尽快收敛于切换平衡点。

2.1 最优切换律设计

引理1如果切换系统的所有子系统具有共同的Lyapunov函数V(x)，其中V(0)=0，并满足

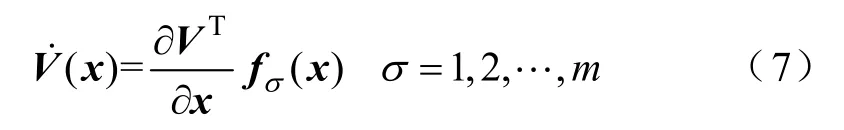
则切换系统在任意切换路径渐近稳定。

对于双向AC-DC而言，由于其含有储能元件，所以本文选择其储能函数作为共同Lyapunov函数，设F=diag{L, L, L}，则有共同Lyapunov函数

设计切换律

如果能够证明在该切换律下，切换系统整个运行区间都能够保证，则表示切换系统将能够收敛于期望的切换平衡点，而且收敛速度最快。

证明:设τ 为满足的所有向量集合，定义切换系统各个子系统凸组合为

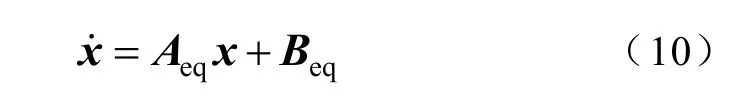
令ζ=x-x*，式（10）可以变化为

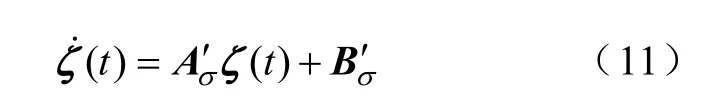
式中

切换系统共同Lyapunov函数的导数可以表示为

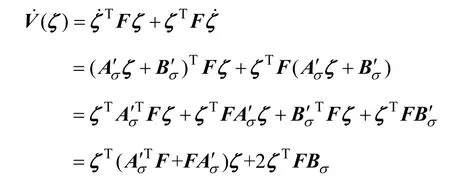
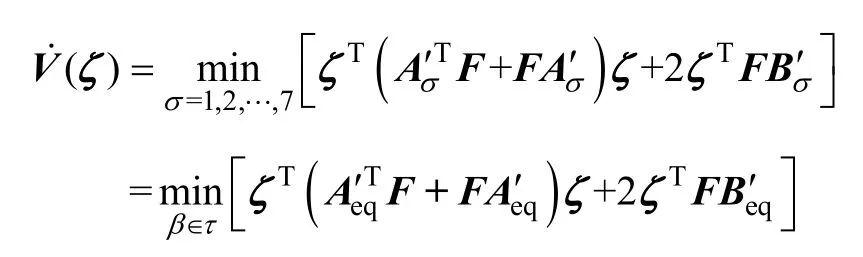
由 AC-DC切换系统模型可知，无论β如何取值，始终有=d iag ｛ - 2R, - 2R, - 2R｝＜0。

将x*=(i*a, i*b, i*c)T代入式（11）得

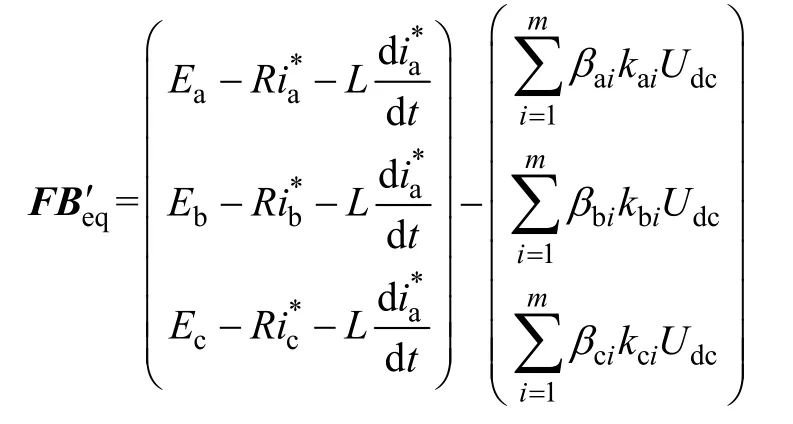
根据双向 AC-DC电路的物理特性可知，正常工作时，双向AC-DC直流侧电压Udc大于其交流侧电压Ep(p=a, b, c)减去线路阻抗上的压降(电阻和电感上的压降)，因此存在一组βi(0＜βi＜1)，使得FBeq≤0，从而可以得到min[2ζTFBeq]≤0。

2.2 基于单步预测的切换律离散化

设 AC-DC变换器采用固定周期采样，采样周期为ΔT，设采样周期开始时双向 AC-DC变换器状态为X(t)，AC-DC每次都在下一个采样周期更新开关管的控制型号，当采样周期ΔT足够小时，有

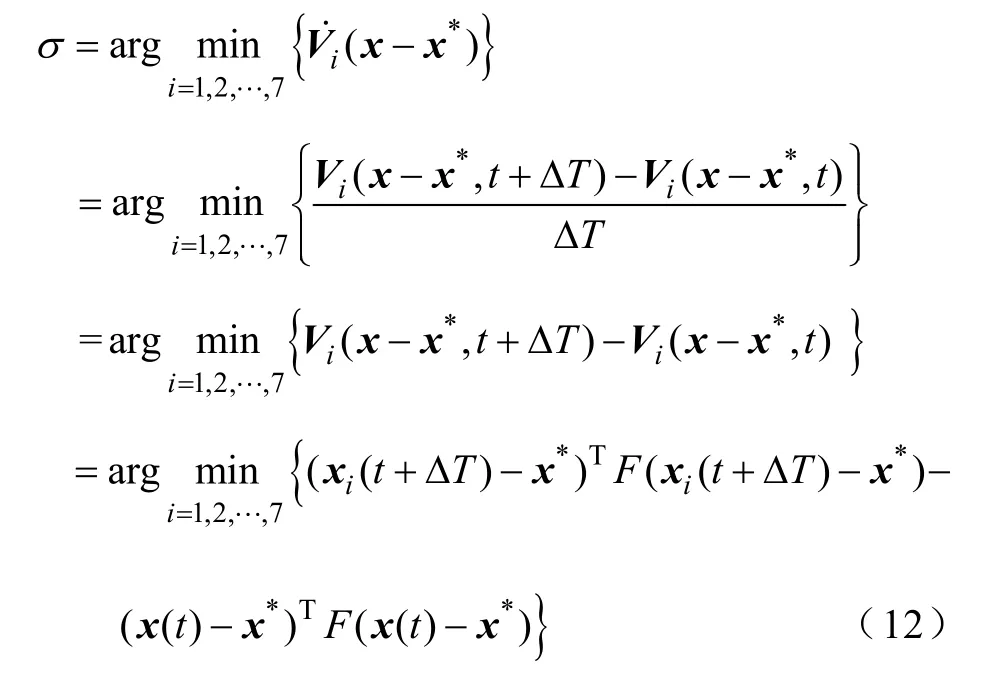
式中，x(t)为t时刻的实时采样值，x*为给定，因此公式的后一项为确定数值，对σ的选择没有影响，上式可以进一步简化为

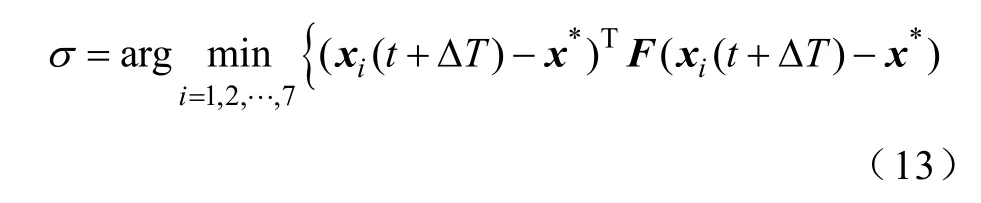
对线性系统状态方程进行求解，可以得到

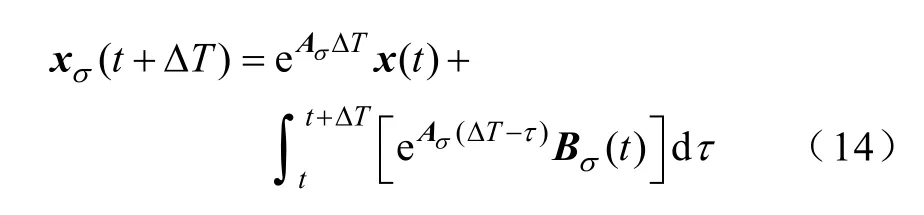
考虑到实际工作中，AC-DC系统采样速度很快，可以认为在一个采样周期内U(t)、E(t)均保持不变，为了方便数字处理器运算，用状态变量的商差代替微商对上式进行离散化

综上，最优切换律的物理意义可以由图2所示。当切换系统选择不同的切换路径时，经过一个采样周期后得到的不同的状态变量xi(t+ΔT)，各xi(t+ΔT)和期望的状态点x*的距离Ji也不相同，最优切换律实际上选择了一个离x*最短距离的模态为下一个周期的控制信号，从而保证系统收敛最快。

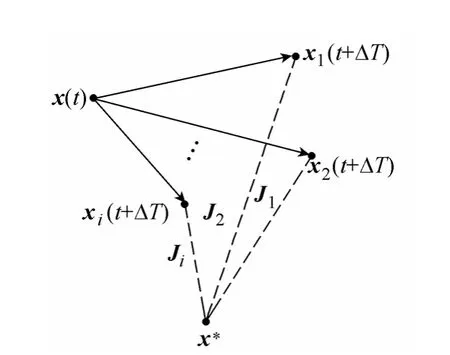
图2 最优切换控制序列物理意义Fig.2 Principle of optimal switching path

3 交直流混合微电网中双向AC-DC的控制策略

在交直流混合微网、电池储能等多数场合中，双向AC-DC变流器被用来控制系统交流侧和直流侧间的能量流动，以保证交直流侧能量平衡，维持直流母线电压恒定。为此采用电压电流双闭环控制策略，控制策略如图3所示。其中电压外环采用PI控制，以直流母线电压稳定为控制目标。为了防止电压扰动造成频繁切换，采用了滞环给定方式，和分别为整流和逆变过程电压给定。整流和逆变分别采用正向和负向电压调节器，二者输出限幅后相加作为电流内环的给定，＞0时系统工作于整流状态，双向变换器从交流侧传递能量到直流母线；＜0时工作于逆变状态。为保证系统工作在单功率因数状态时，将设置为0。

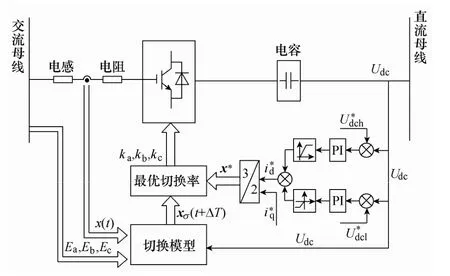
图3 双向AC-DC变换器控制策略图Fig.3 Block diagram of control of bi-directional AC-DC converter

4 仿真分析与实验验证

4.1 仿真分析

在Matlab/Simulink 环境下搭建仿真模型，双向AC-DC参数如下:滤波电感L=7mH；线路阻抗R=2，采样周期ΔT=100μs；直流母线电容C=470μF；电压外环PI调节器比例常数Kp=0.8，积分常数Ki=0.2；整流和逆变运行时的Udc分别为685V和700V；电网电压为380V/50Hz。

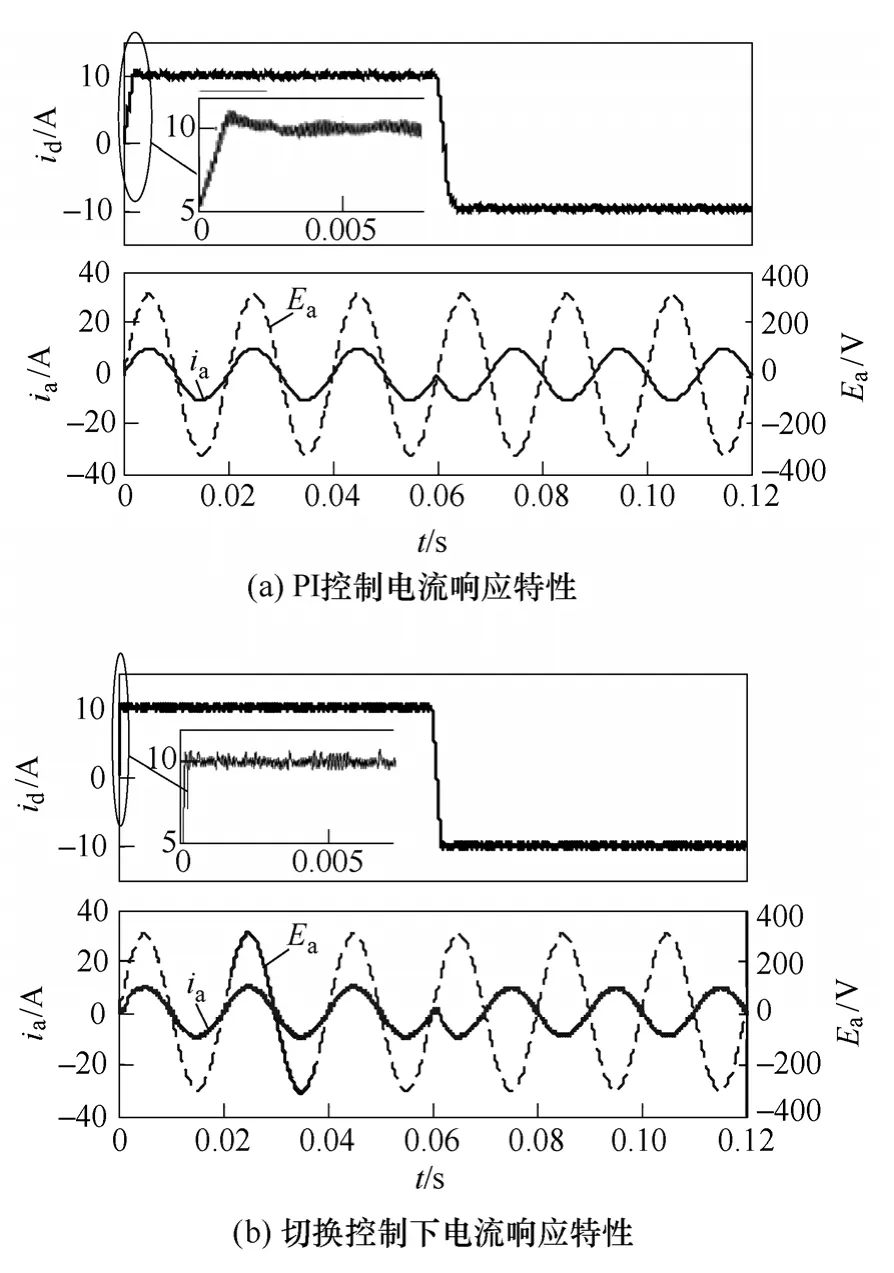
图4 电流环仿真结果Fig.4 Current loop simulation results

图5是模拟微网功率流动变化过程的双闭环控制的仿真结果，仿真过程中对直流母线突加突卸2kW负载，双向变换器由1kW逆变→1kW整流→1kW逆变。由图5可知，负载切换过程中直流母线电压能够在约0.01s内稳定，电压波动幅值最大不超过7%，仿真结果表明，本文控制策略能够有效控制微网中交流和直流间的功率流动，维持电压稳定。

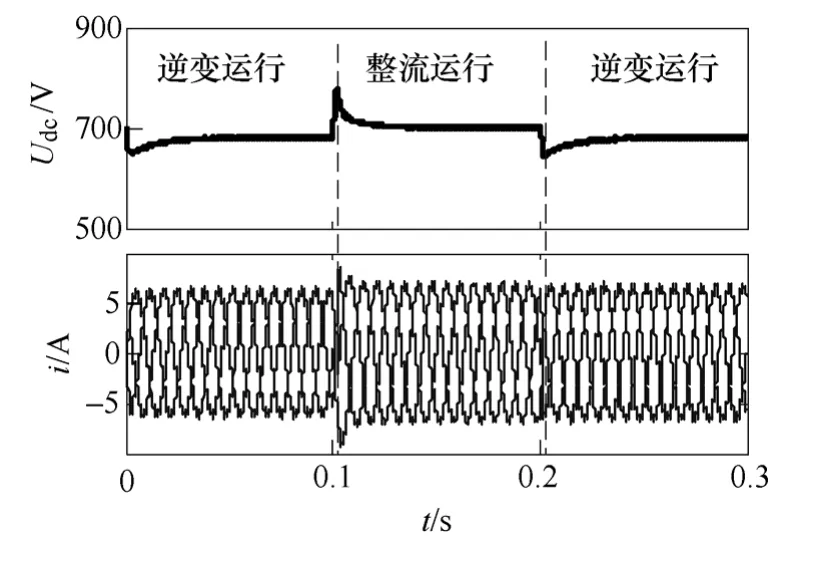
图5 双闭环仿真结果Fig.5 Double-loop simulation results

4.2 实验验证

采用与仿真相同的参数，在实验室搭建了AC-DC双向变换器实验系统，其中主控制器采用dsPACE MicroautoboxII-1401，采用Chroma-62150H-1000S可编程电源模拟可再生能源向直流母线提供功率，电阻箱用来模拟用电负载。设置系统采样周期ΔT=100μs，开关死区Td=3μs。

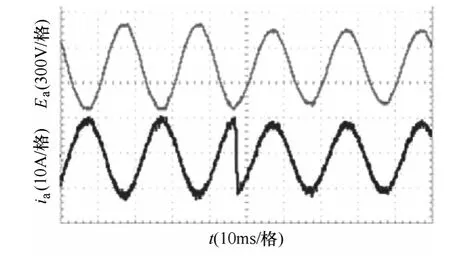
图6 电流环实验结果Fig.6 Experimental waveforms of current loop control

双闭环实验结果如图7所示，其中图7a是变换器由逆变切换整流过程中a相电压电流波形和直流母线电压变化图。其中图7b是变换器由整流切换逆变过程中a相电压电流波形和直流母线电压变化图。由实验结果可知，双向AC-DC工作过程中电流正弦度良好，且可以实现整流和逆变之间的平滑无缝切换。

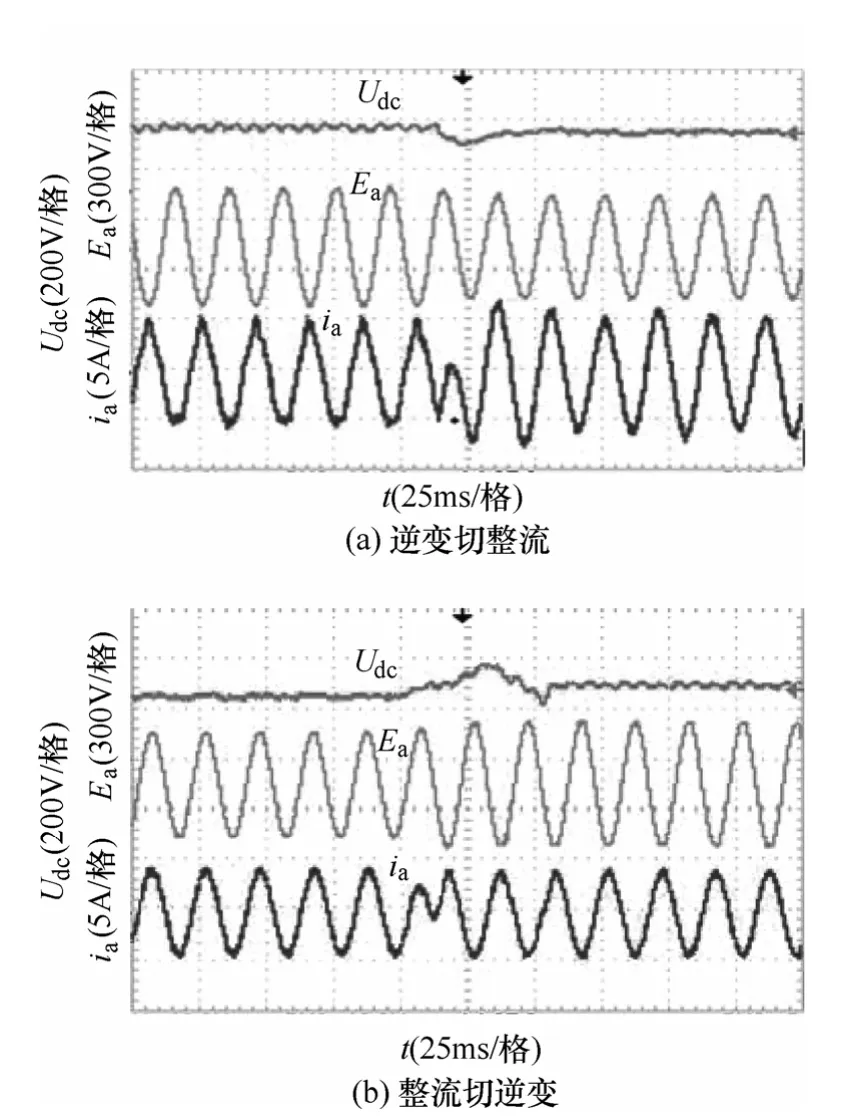
图7 双闭环实验结果Fig.7 Experimental waveforms of double closed-loop control

5 结论

本文基于切换理论建立了双向AC-DC变换器的切换动态模型，以系统储能函数能量收敛最快为目标设计了最优切换序列控制算法，并证明了其稳定性。通过切换系统单步预测模型对切换律进行离散化。仿真和实验结果表明系统静态和动态控制效果都较好；验证了模型的正确性以及控制策略的有效性。

相对于传统的平均状态建模方法，切换系统理论建模更利于描述电力电子电路的变结构行为，而且通过设计切换路径完成开关管控制，不需要任何PWM调制策略，原理简单、实现容易。

[1] Marnay C, Robio F J, Siddiqui A S. Shape of the micro-grid[C]. IEEE Power Engineering Society Winter Meeting, Columbus, OH, USA, 2001, 1:150-153.

[2] 王成山, 李鹏. 分布式发电、微网、智能配电网的发展与挑战[J]. 电力系统自动化, 2010, 34(2):10-14.

Wang Chengshan, Li Peng, Development and challenges distribution generation, the micro-gird and smart distribution system[J]. Automation of Electric Power Systems, 2010, 34(2): 10-14.

[3] Lasseter R H, Akhil A, Marnay C, et al. White paper on integration of distributed energy resources, the certs microgrid concept[C]. Consortium for Electric Reliability Technology Solutions, 2002: 1-27.

[4] Barnes M, Ventakaramanan G, Kondoh J, et al. Real world micro-grids—an overview[C]. IEEE International Conference on System of Systems Engineering, San Antonio, TX, USA, 2007: 1-8.

[5] 吴卫民, 何远彬, 耿攀, 等. 直流微网研究中的关键技术[J]. 电工技术学报, 2012, 27(1): 98-113.

Wu Weimin, He YuanBin, Geng Pan, et al. Key technologies for DC micro-grids[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 98-113.

[6] Salehi V, Mohamed A, Mohammed O A. Implementation of real-time optimal power flow management system on hybrid AC/DC smart microgrid[C].Industry Applications Society Annual Meeting (IAS),2012 IEEE Digital Object Identifier, 2012: 1-8.

[7] Yukita K, Shimizu Y, Goto Y, et al. Study of AC/DC power supply system with DGs using parallel processing method[C]. Proceedings of IEEE International Power Electronics Conference, Sapporo,Japan, 2010.

[8] Liu X, Wang P M, Loh P C. A hybrid AC/DC microgridand its coordination control[J]. IEEE Transactions on Smart Grid, 2011, 2(2): 278-286.

[9] 张犁, 吴田进, 冯兰兰, 等. 模块化双向 AC/DC变换器并联系统无缝切换控制[J]. 中国电机工程学报, 2012,32(6): 90-96.

Zhang Li, Wu Tianjin, Feng Lanlan, et al. Seamless switching control for modular bi-directional AC/DC converter parallel systems[J]. Proceedings of the CSEE, 2012, 32(6): 90-96.

[10] 马皓, 祁峰, 张霓. 基于混杂系统的DC-DC变换器建模与控制[J]. 中国电机工程学报, 2007, 27(36):92-96.

Ma Hao, Qi Feng, Zhang Ni. Modeling and control for DC-DC converters based on hybrid system[J].Proceedings of the CSEE, 2007, 27(36): 92-96.

[11] Decarlo R A, Branicky M S, PetterssonS, et al.Perspective sand results on the stability and stabilizability of hybrid systems[J]. Proceedings of the IEEE, 2000, 88(7): 1069-1082.

[12] Deaecto G S, Geromel J C, Garcia F S, et al. Switched affine systems control design with application to DC-DC converters[J]. IET Control Theory and Applications, 2010, 4(7): 1201-1210.

[13] 胡宗波, 张波, 邓卫华, 等. 基于切换线性系统理论的DC/DC 变换器控制系统的能控性和能达性[J].中国电机工程学报, 2004, 24(12): 165-170.

Hu Zongbo, Zhang Bo, Deng Weihua, et al.Controllability and reach ability of DC/DC converters as switched linear system[J].Proceedings of the CSEE,2004, 24(12): 165-170.

[14] 李琼林, 刘会金, 宋晓凯, 等. 基于切换系统理论的三相变换器建模及其稳定性分析[J]. 电工技术学报, 2009, 24(11): 90-95.

Li Qionglin Liu Huijin Song Xiaokai, et al. Modeling and stability analysis of three-phase converter based on switching system theory[J]. Transactions of China Electrotechnical Society, 2009, 24(11): 90-95.

[15] 李春文, 汤洪海, 郑雪生, 等. 三相 APF的切换系统建模与二次最优控制[J]. 中国电机工程学报,2008, 28(12): 66-72.

Li Chunwen, Tang Honghai, Zheng Xuesheng, et al.Modeling and quadratic optimal control of threephase apf based on switched system[J]. Proceedings of the CSEE, 2008, 28(12): 66-72.

[16] 郭晓云, 刘会金, 曹玉胜. 基于切换仿射线性模型的三相 APF电流控制方法[J]. 中国电机工程学报,2011, 31(4): 59-66.

Guo Xiaoyun, Liu Huijin, Cao Yusheng. A novel current control method for three-phase apf based on switched affine model[J]. Proceedings of the CSEE,2011, 31(4): 59-66.

[17] 李继方, 韩金刚, 汤天浩. 基于切换系统的开关变换器统一建模[J]. 华南理工大学学报(自然科学版),2011, 39(10):157-163.

Ma Hao, Qi Feng, Zhang Ni. Unified modeling of switching converters based on switching system[J].Journal of South China University of Technology(Natural Science Edition), 2011, 39(10): 157-163.

[18] 程代展, 郭宇蓦. 切换系统进展[J]. 控制理论与应用, 2005, 22(12): 954-960.

Cheng Daizhan, Guo Yuqian. Advances on switchedsystems[J]. Control Theory and Applications, 2005,22(12): 954-960.