大型潜水电机混合偏心时转子副临界振动的研究

鲍晓华 李福英 方 勇 王汉丰 程志恒 狄 冲 梁 娜

（合肥工业大学电气与自动化工程学院 合肥 230009）

1 引言

大型潜水电机主要用于大型矿山排水、城市污水处理系统以及抢险救灾、地表灌溉等场合。随着潜水电机制造业的发展，潜水电机的需求数量不断增长，在潜水电机的设计和制造过程中，由于材质的不均匀性，或是机械加工和装配上的误差，使得定转子存在一定的偏心。大型潜水电机常年工作于深水之下，其特殊的工作环境对转子振动提出新的挑战，又由于其检修工作的困难，这要求潜水电机拥有极高的运行稳定性。正确计算和预测故障下的转子振动状态，不仅可以优化电机设计，还为今后电机安全高速运行奠定了坚实的理论基础。N. M.Elkasabgy等学者指出，80%定转子偏心源于机械装配，而60%的机械故障源于偏心[1-3]。因此偏心下电机性能参数研究是必要的。

根据偏心几何的特征，气隙偏心可以分为轴向均匀偏心和轴向不均匀偏心两种基本类型。其中，轴向均匀偏心又可分为静态偏心（SE）、动态偏心（DE）以及混合偏心（ME）[4,5]，轴向不均匀偏心即斜偏心（IE）[6]。静偏心指定转子不同心，转子以自身几何轴心为旋转轴。动偏心指定转子不同心，但转子以定子的几何轴心为旋转轴。混合偏心指静偏心和动偏心的组合，即定转子不同心，转子以正常电机定转子的几何中心为旋转轴（见图1）。目前国内针对电机气隙偏心的研究相对国外较少，气隙偏心研究多为静态偏心、动态偏心和混合偏心特征量[7-8]的提取，很少涉及偏心下转子振动问题。实际上，静态偏心总是和动态偏心同时存在。由于制造和安装的误差，即使新制造的电机也会存在固有的静态偏心[9]。且在电机运行过程中，转子受到初始单边磁拉力的影响而弯曲，又产生一定的动偏心。

根据电机设计及电磁基础理论，电机振动可大致归类为三种：电磁振动、机械振动和空气动力振动。其中电磁振动和机械振动一直是国内外电机学者们研究的重要课题，并且取得了一定的研究成果。姚志远等人针对杆截面的突变会降低波传播效率的问题，提出基于连续变截面兰杰文振子的设计方法，以此优化电机的输出性能[10]。莫岳平等人通过 ANSYS有限元模态分析，阐述了最优振动模态的选择[11]。K.N.S等人建立定转子三维模型，采用3D FEA方法，分析了由多种因素引发的电机振动[12]，但并未考虑转子副临界共振对电机的安全运行的影响。

由转子动力学可知，由于转子非对称刚性或是转子重力的影响，致使电机转子工作在某一转速时，转子挠度达到峰值，此时转子转速大小为临界转速大小的一半，这样的转速被称为副临界转速，或称为次临界转速以及亚临界转速。副临界转速时产生的转子共振现象简称为副临界振动。

随着计算机的发展及仿真软件的完善，在电机转子振动[13]，偏心建模[14,15]，偏心仿真[16,17]，偏心检测[18,19]等方面国内外学者已经做了很多研究。Kyung-Ho-Ha等人分析了不平衡电磁力对转子涡动轨迹的响应，通过预测转子轴承系统的机械动力性能降低振动，优化电机性能[20]。在非对称转子副临界转速理论计算分析方面，林富生等人理论分析并实验研究了带初始弯曲的刚度不对称转子的稳定性和动态响应，提出副临界现象的存在[21]。针对某种特种电机进行具体的副临界共振分析，尤其是定转子偏心状态下，却研究甚少。本文针对大型潜水电机，基于副临界转子振动对电机的影响，分析副临界转速的部分影响因素，阐述副临界转速与额定转速的关系和副临界共振机理的发生条件。

大型潜水电机由于其较大的转子质量，以及其特殊的工作环境，使其转子共振性能不同于一般的感应电机和高速电机。为了避免共振，降低转子挠度，更好的优化电机性能，只研究临界转速时转子的共振现象是远远不够的。本文引入转子副临界状态下的共振概念，分析了混合偏心对转子副临界共振的影响，研究了副临界转速与偏心量的关系，探讨了副临界转速与潜水深度的关系，并在此基础上实现了对存在混合偏心电机的谐波共振的部分研究。最后以一个 4 000kW，4极潜水电机为例进行验证。

2 混合偏心转子模型的建立

基于混合偏心转子的运动特性，建立了混合偏心转子仿真模型和计算模型，如图1所示。本文的计算仿真分析均建立在图1所定义的坐标系上。

图1 混合偏心转子计算模型Fig.1 The calculation model of mixed eccentricity

由图1可知气隙长度表达式可以表达为

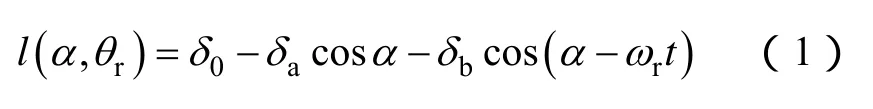
式中δ0——平均气隙长度；

δa,δb——静态偏心，动态偏心量；

α——定子空间角度；

ωr——转子旋转角速度；

气隙长度的逆表达式可以表示为

由此式（2）可大致表示为

表1 分析模型指标和材料属性Tab.1 The index and material properties for analysis model

本文针对4 000kW，电机气隙为3.5mm的大型湿式潜水电机进行仿真，分析其混合偏心转子状态下的电机转子性能。表1列举了仿真模型的性能参数和材料属性。实际应用中可以通过套筒的方法实现混合偏心，即在轴承内外圈均装配套筒，继而通过调节套筒的厚度实现混合偏心的效果[22]。

3 混合偏心对转子副临界共振的影响

由于混合偏心转子的影响，电机气隙磁导发生变化，产生不平衡电磁拉力，极大程度的影响了电机系统的电磁刚度，这不仅增加了转子的稳定挠度，降低了转子的临界转速，还影响了转子的共振点和共振状态，危及电机的安全运行。

3.1 混合偏心时的不平衡电磁力

转子混合偏心时，由于气隙磁导的变化，定转子气隙间不平衡磁拉力也发生了变化。本文建立了电机模型，采用有限元方法对气隙间磁感应强度进行仿真。并通过场计算器对仿真结果进行后处理，实现气隙间电磁力的仿真及分析。根据工程电磁场理论可知

式中，A为矢量磁位。

假设铁心磁导率无限大，其定转子间磁感应强度如图2所示。

图2 气隙磁通密度图Fig.2 The flux density for air-gap

由于假设的偏心量比较小，因此气隙磁通密度变化不明显。图2为1%的静偏心（SE）、1%动偏心（DE）时的混合偏心气隙磁通密度变化图。由于齿槽谐波、剖分等因素，磁通密度变化与标准的正弦波存在一定的误差，影响电磁力的幅值，但是不改变其频率成分及变化趋势。

为适应气隙长度的变化，有限元计算中气隙网格变化如图3a所示，图3b为定子电流变化图。

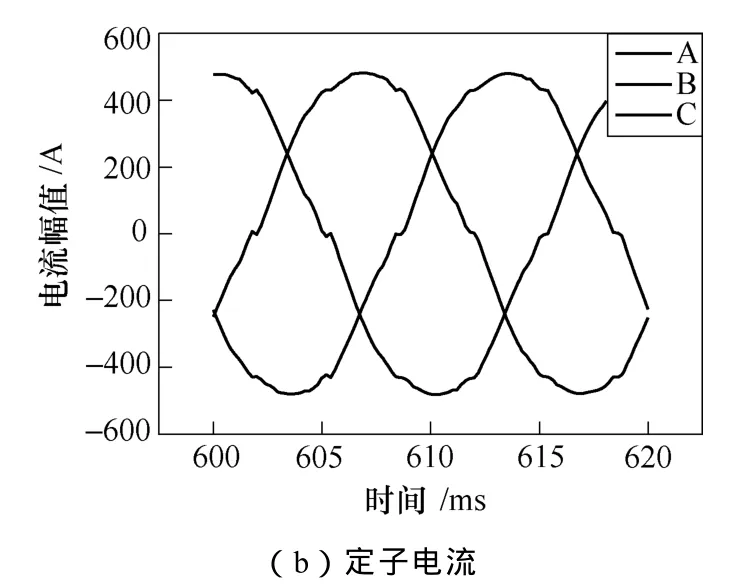
图3 定子电流图Fig.3 Plot mesh of air-gap and stator current

根据Maxwell应力张量法，电机定转子气隙间径向电磁力矢量可表示为

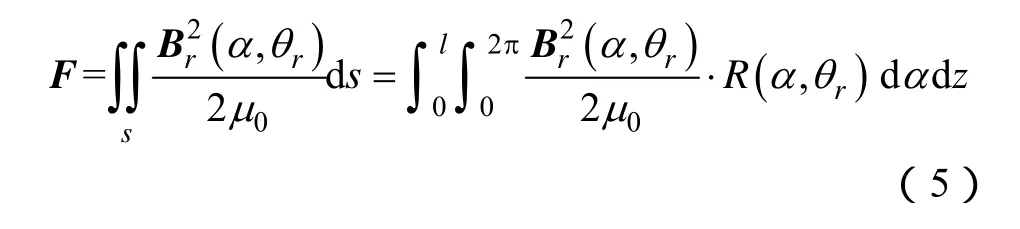
式中l——铁心长度；

R(α,θr)——平均气隙半径（见图1），其可表示为

式中，转子旋转角度θr=ωrt。

假设径向气隙电磁力全由径向磁通密度产生，即忽略切向磁通密度，则在一个电周期内，不同混合偏心下气隙电磁力的时间谐波的傅里叶分解如图4所示，从图中可以得到不同混合偏心下的各种谐波频率，其中存在接近于转子固有频率（见表 2）的谐波频率。

图4 傅里叶分解图Fig.4 Fourier decomposition

图5描绘了0.4s时不同混合偏心度下转子固有频率与同等条件下谐波频率的对比，其中谐波频率是由非线性磁拉力所产生，从图中可以得出，作用于转子上的激振力频率与转子固有频率比较接近，可能激起转子共振。（注：图中的点为该偏心量下接近固有频率的激振频率值。）

图5 固频和激频的关系Fig.5 The frequency relation between nature and excitation

3.2 混合偏心时的副临界特性

电机作为一个机电耦合系统，是一个磁与力的综合体。当转子存在混合偏心时，其不仅影响了气隙磁场、系统性能，还改变了转子的临界转速，影响转子的副临界特性。考虑到实际潜水电机应用中采用的是滚动轴承, 可以假设电机支承方式为刚性支承。

副临界转速的求解一般采用解析法和有限元法，其解析法表达式如下：

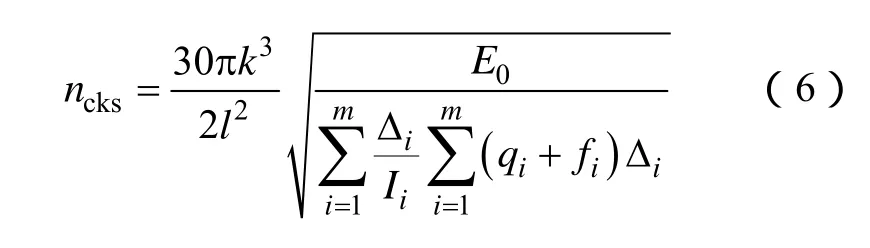
式中k——临界转速的阶数；

l——转轴在两个支点间的长度；

E0——基准弹性模量；

Δi——位置函数；

Ii——各轴段截面惯性矩；

qi——各轴段质量线密度；

fi——各轴段磁拉力线密度。

根据电机设计原理，考虑实际情况下的电机类型、磁场分布等影响，其各轴段铅垂方向磁拉力总和可表示为Fi=0 .3πDlefδe/δ/ 2μ0，为保持fi和qi单位的一致性，其各轴段磁拉力线密度总和可表示为

式中D——转子外径。

混合偏心气隙长度δe可以表示为

式中δs——静偏心量；

δr——动偏心量；

k——拟合系数（此处取0.32）。

将表达式（8）代入式（7），可以得出副临界转速具有时变特性（见图6）。为减少仿真时间，节约资源，取电机稳定运行区域0.4～0.8s。

从图6可以看出，副临界转速在稳定区域0.4～0.8s间呈现先增后减的趋势。在不同的混合偏心度下，副临界转速变化的范围也有所不同，而且静态偏心的影响程度高于动态偏心，动态偏心受时间的影响度高于静态偏心。

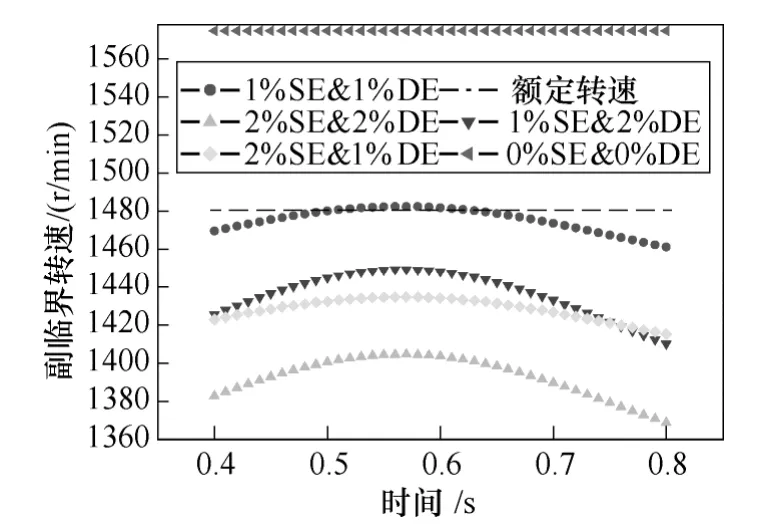
图6 副临界转速与时间的关系Fig.6 The variation of sub-critical speed with time

图6阐述了，当转子存在1%的静偏心和1%的动偏心时，转子的副临界转速最接近的额定转速，易发生副临界共振现象，应予以避免。

本文采用解析-有限元法，分析混合偏心度对副临界转速的影响。根据转子动力学，将不平衡磁拉力等效为作用于转子上的电磁刚度，则其副临界转速可简化表示为

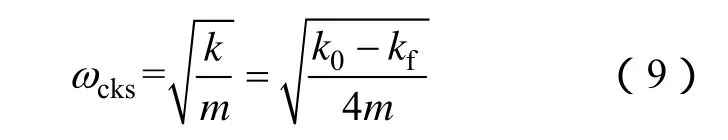
式中kf——电磁刚度；

k0——弯曲刚度（见图7）；

m——转子铁心质量；

k——等效后的转子刚度，根据材料力学，等效转子刚度可表示为

式中E——弹性模量；

J——转动惯量；

l——铁心段长度；

a——仿真等效误差系数，考虑到材料、长度仿真等多种等效与误差，本文中a=0.97（由图7a解析得出）。

表2列出了不同转子混合偏心度下固有频率和临界转速的数值，以0.4s时的数据为例，其他时刻变化趋势一致。由该表格可以得出转子固有频率随混合偏心度增加而降低，如图7所示。

表2 固有频率和临界转速对比表Tab.2 The natural frequency and critical speed

图7 三维仿真转子模型Fig.7 3-D simulation model of rotors

图7为转子模型和转子初始附加载荷值。不平衡磁拉力作用于图中轴段z1～z2，所以可通过改变该段的等效转子刚度以达到仿真的效果。

以0.4s、0.5s、0.6s时副临界转速随偏心度的变化为例，分析副临界转速与偏心度的关系如图8所示。由图8和表格2可以得出，整体上副临界转速随偏心度的增加而降低，但在混合偏心下，对比不同的静偏心和动偏心时（即被对比模型同时存在不同的静偏心和动偏心，例如本文中1%SE&2%DE与2%SE&1%DE，即图中2和3位置处），由于仿真误差，副临界转速幅值存在一定的波动。由于解析计算（式（7）～式（9））中存在经验系数，使得理论计算值与仿真值之间存在一定的误差（见图8b）。

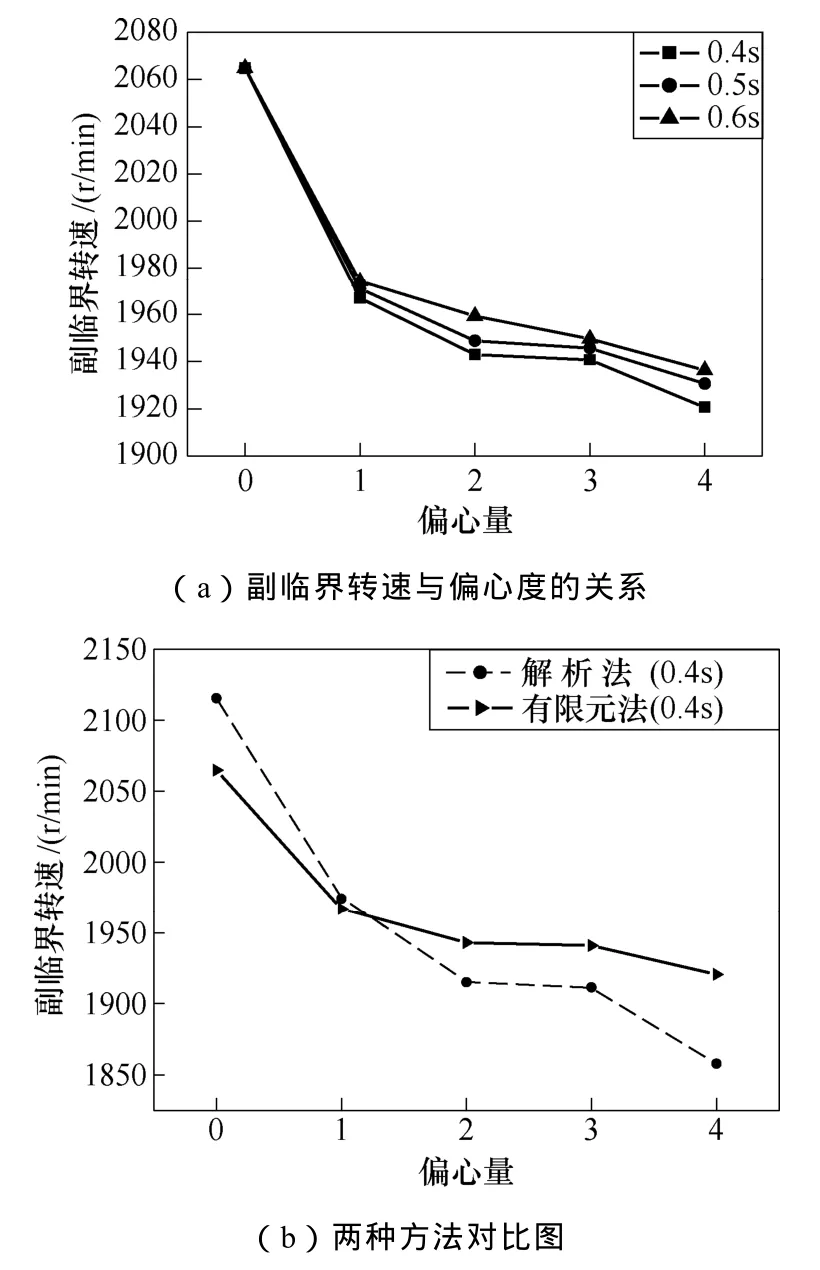
图8 副临界和偏心度的关系Fig.8 The variation of sub-critical speed with eccentricity

随着时间的增加，转子副临界转速的变化区域位于0.4s上下波动，即转子副临界转速随时间呈不规则的周期性变化。图8中的0～4分别代表偏心度为 0%SE&0%DE、1%SE&1%DE、1%SE&2%DE、2%SE&1%DE、2%SE&2%DE。

4 潜水深度对副临界共振的影响

大型潜水电机一般工作于水深1 000m以下，受到水压的影响，电机性能发生变化，这不仅降低副临界转速，还引发转子振动。本文采用有限元-解析法对其进行分析。

考虑到大型潜水电机特殊的工作环境，加入潜水深度的影响，式（6）可表示为

式（9）可表示为

式中hi,kh——水压密度和等效的水压刚度。

由于水下压强未直接作用于转子上，本文采用等效的方法，利用Ansys软件仿真压强对定子挠度的影响（见图8），得到气隙偏心量的表达式为

式中δh——压强引起的气隙偏心量（见图 9），以最大挠度值为主，k取0.32。

图9 定子挠度位移云图Fig.9 The displacement nephogram of stator deflection

图 10为副临界转速随潜水深度和时间变化图,从图中可以得出转子副临界转速随潜水深度的增加而降低。但随时间呈不规则变化，因此在电机投入工程运行前，需要模拟多段时间值，确保电机的安全运行。图中时间范围是0.4～0.6s，潜水深度范围为0～5 000m。

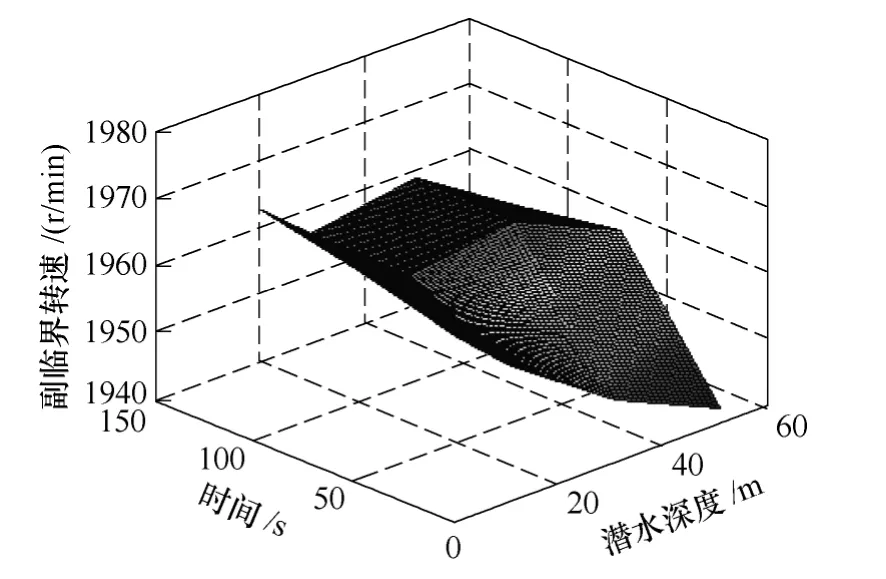
图10 副临界转速和潜水深度的关系Fig.10 The variation of sub-critical speed with diving depth

5 结论

随着潜水电机高功率、高转速的发展，转子振动问题的研究迫在眉睫。与高速电机相比，大型潜水电机转速相对较低，因此为了更好的利用转子动力学，分析低转速区转子涡动轨迹等问题，本文引入副临界转速，在比较全面考虑大型潜水电机定转子结构特点的基础上，创建了混合偏心下的定转子模型及三维力学分析转子模型。

根据工程电磁场理论，采用有限元方法，分析并仿真了大型潜水电机混合偏心下定转子气隙间磁通密度分布和气隙电磁力激振频率。又通过电磁刚度，耦合磁力效应，分析在不同的混合偏心系统中，转子的副临界转速变化，得到了副临界转速与偏心度的关系：随偏心度的增加而降低。当定转子达到一定的偏心度，副临界转速将接近于电机的额定转速，又考虑到激振频率的存在，易引发转子的副临界共振，危及电机安全运行。

考虑到大型潜水电机特殊的工作环境，计算并仿真了潜水深度对转子副临界转速的影响，得到潜水深度和副临界转速的关系以及副临界转速与时间的关系。

本文的研究可为工程中提高电机可靠运行等方面提供一定的参考，同时为转子动力学的进一步应用奠定了基础。

致谢本文中的样机及相关数据由合肥恒大江海泵业股份有限公司研究院提供，在其研究院工作人员的大力支持下完成，在此向他（她）们表示衷心的感谢。

[1] Elkasabgy N M, Eastman A R, Dawson G E. Detection of broker bar in the cage rotor on an induction machine[J]. IEEE Transactions on Industry Applications, 1992, 28(1): 165-171.

[2] 鲍晓华, 吕强. 感应电机气隙偏心故障研究综述及展望[J]. 中国电机工程学报, 2013, 33(6): 93-100.

Bao Xiaohua, Lü Qiang. Review and prospect of air-gap eccentricity faults in induction machines[J].Proceedings of the CSEE, 2013, 33(6): 93-100.

[3] Xia Changliang, Song Zhanfeng. Wind energy in China: current scenario and future perspectives[J].Renewable and Sustainable Energy Reviews, 2009,13(8): 1966-1974.

[4] 赵向阳, 葛文韬. 基于定子电流监测无刷直流电动机转子动态偏心的故障模型仿真研究[J]. 中国电机工程学报, 2011, 31(36): 124-130.

Zhao Xiangyang, Ge Wentao. Simulation research of fault model of detecting rotor dynamic eccentricity in brushless DC motor based on motor current signature analysis[J]. Proceedings of the CSEE, 2011, 31(36):124-130.

[5] Faiz J, Ebrahimi B M, Akin B, et al. Dynamic analysis of mixed eccentricity signatures at various operating points and scrutiny of related indices for induction motors[J]. IET Electric Power Applications, 2010,4(1): 1-16.

[6] Li Xiaodong, Wu Qing, Nandi S. Performance analysis of a three-phase induction machine with inclined static eccentricity[J]. IEEE Transactions on Industry Applications, 2007, 43(2): 531-541.

[7] Hossein Torkaman, Ebrahim Afjei, Peyman Yadegari.Static, dynamic, and mixed eccentricity faults diagnosis in switched reluctance motors using transient finite element method and experiments[J]. IEEE Transactions on Magnetics, 2012, 48(8): 2254-2264.

[8] Ebrahimi B M, Faiz J. Diagnosis, performance analysis of three-phase permanent magnet synchronous motors with static, dynamic and mixed eccentricity[J]. IET Electr. Power Appl., 2010, 4(1): 53-66.

[9] Dorrell D G, Thomson W T, Roach S. Analysis of airgap flux, current, and vibration signals as a function of the combination of static and dynamic airgap eccentricity in 3-phase induction motors[J]. IEEE Transactions on Industry Applications, 1997, 33(1):24-34.

[10] 姚志远, 杨东, 赵淳生. 杆结构直线超声电机的结构设计和功率流分析[J]. 中国电机工程学报, 2009,29(24): 56-60.

Yao Zhiyuan, Yang Dong, Zhao Chunsheng. Structure design and power flow analysis of bar-structure linear ultrasonic motors[J]. Proceedings of the CSEE, 2009,29(24): 56-60.

[11] 莫岳平, 胡敏强, 徐志科, 等. 超声波电机振动模态有限元分析[J]. 中国电机工程学报, 2002, 22(11):93-97.

Mo Yueping, Hu Minqiang, Xu Zhike, et al. The finite element analysis on the vibration mode of ulirasonic motor[J]. Proceeding of the CSEE, 2002, 22(11):93-97.

[12] Srinivas K N, Arumugam R. Analysis and characterization of switched reluctance motors: part II –flow, thermal, and vibration analyses[J]. IEEE Transactions on Magnetics, 2005, 41(4): 1321-1332.

[13] 何成兵, 顾煜炯, 邢诚. 短路故障时汽轮发电机组轴系弯扭耦合振动分析[J]. 中国电机工程学报,2010, 30(32): 84-90.

He Chengbing, Gu Yüjiong, Xing Cheng. Coupled flexural and torsional vibrations analysis of turbine generator shaft systems caused by circuit fault[J].Proceedings of the CSEE, 2010, 30(32): 84-90.

[14] 孙晓东, 陈龙, 杨泽斌, 等. 考虑偏心及绕组耦合的无轴承永磁同步电机建模[J]. 电工技术学报,2013, 28(3): 63-70.

Sun Xiaodong, Chen Long, Yang Zebin, et al. Modeling of a bearingless permanent magnet synchronous motor considering rotor eccentricity and coupling relationship of windings[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 63-70.

[15] 仇志坚, 邓智泉, 王晓琳, 等. 计及偏心及洛仑兹力的永磁型无轴承电机建模与控制研究[J]. 中国电机工程学报, 2007, 27(9): 64-70.

Qiu Zhijian, Deng Zhiquan, Wang Xiaolin, et al. Study on the modeling and control of a permanent magnet type bearingless motor considering rotor eccentricity and Lorenz force[J]. Proceedings of the CSEE, 2007,27(9): 64-70.

[16] Dooso Hyun, Sungho Lee, Jongman Hong, et al.Detection of airgap eccentricity for induction motors using the single-phase rotation test[J]. IEEE Transactions on Energy Conversion, 2012, 27(3): 689-696.

[17] Lamamura B A T, et al. Study of static and dynamic eccentricity of a synchronous generator using 3-D FEM[J]. IEEE Transactions on Magnetics, 2010, 46(8):3516-3519.

[18] 孙一航, 武建文, 廉世军, 等. 结合经验模态分解能量总量法的断路器振动信号特征向量提取[J]. 电工技术学报, 2014, 29(3): 228-236.

Sun Yihang, Wu Jianwen, Lian Shijun, et al. Extraction of vibration signal feature vector of circuit breaker based on empirical mode decomposition amount of energy[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 228-236.

[19] Ebrahimi Bashir Mahdi, et al. Advanced eccentricity fault recognition in permanent magnet synchronous motors using stator current signature analysis[J]. IEEE Transactions on Industrial Electronics, 2014, 61(4):2041-2052.

[20] Kyung Ho Ha, et al. Orbital analysis of rotor due to electromagnetic force for switched reluctance motor[J]. IEEE Transactions on Magnetics, 2000, 36(4):1407-1411.

[21] 林富生, 孟光. 有初弯的刚度非对称转子的动力学特性分析及实验研究[J]. 应用力学学报, 2002,19(3): 96-101, 168-169.

Lin Fusheng, Mengguang. The analysis and experiment of dynamics for asymmetric rotor with initial bending[J]. Chinese Journal of Applied Mechanics, 2002,19(3): 96-101, 168-169.

[22] Subhasis Nandi, Sang Bin Lee. et al. Detection of eccentricity faults in induction machines based on nameplate parameters[J]. IEEE Transactions on Industrial Electronics, 2011, 58(5): 1673-1683.