基于贮存可用度的导弹武器装备检测周期确定方法

陈智芳

(中国空空导弹研究院，河南 洛阳 471009)

0 引 言

导弹武器装备的检测周期影响着其贮存可用度，检测周期越短，且通过检测发现故障即进行修复，就可确保导弹武器装备具有较高的贮存可用度，反之，贮存可用度就会较低。为此，许多专家学者开展了定期检测方面的研究，这些研究主要从可靠性角度出发，探讨了定期检测对贮存可靠性的影响［1－2］，建立了贮存可靠性模型［3－4］，给出了可靠性模型参数估计［5－6］，并进行了模型的数字仿真研究［7］。

然而，仅从贮存可靠性角度来确定检测周期存在一定不足，未考虑到维修性、测试性、保障性等因素的影响。对于导弹武器装备，更应该关注其贮存可用度，因为贮存可用度综合考虑了可靠性、维修性、测试性、保障性等因素，直观反映了导弹武器装备一旦需要即可投入使用的能力。为此，本文认真分析了导弹武器装备的贮存过程以及贮存可用性与可靠性之间的关系，建立了贮存可用度与检测周期之间的数学模型，并给出了检测周期的确定方法，为工程实践中更合理地确定检测周期、更方便地开展使用维护工作提供了参考。

1 导弹武器装备贮存过程分析

随着科学技术与工业能力的发展，导弹武器装备具有了越来越强的长期贮存能力，而导弹武器装备的大部分服役过程是在贮存状态中度过的。贮存过程中，受温度、湿度等环境因素的影响，导弹武器装备不可避免地会出现故障，如:温度变化过快会使装药表面结露受潮，并会导致电子晶体管损坏;湿度过大会导致橡胶件塑性和强度下降，还会使火帽中的击发药作用不可靠甚至瞎火［8］。这就要求在其出现故障后，能尽早发现并及时修复好，始终确保其可用度保持在一定水平以上，以满足战备任务需求。

为此，需要对处于贮存状态的导弹武器装备进行检测。受限于人力、物力、财力等因素，检测不可能每时每刻都进行，只能有间隔、周期性地进行定期检测。然而并不是所有的故障都能通过检测被发现，这反映在故障检测率上，故障检测率是指用规定的方法能够检测到的故障与故障总数之比。在能够发现故障的情况下，就需要对故障进行修复，而修复工作需要在一定时间内完成，这个时间一般是综合考虑战备任务需求、平均维修时间、平均保障资源延误时间等因素后权衡得出的，在相关的技术文件中予以明确。受保障资源、保障能力、管理体制等因素的影响，在该规定时间内完成修复工作具有一定概率，这种概率是维修度。完成修复后，导弹武器装备重新处于贮存状态。

2 基于贮存可用度的检测周期确定方法

2.1 贮存可用性与可靠性关系分析

导弹武器装备的贮存可用性是指处于贮存状态的导弹武器装备在需要开始执行任务的任一时刻，其处于正常(无故障)状态且可投入使用的能力，用贮存可用度来进行度量:

式中:Azc为贮存可用度;Nky为可用产品数;N 为产品总数。

对于可修复产品，其贮存可用性与可靠性、测试性、维修性、保障性等因素有关;对于不可修复产品，其贮存可用性仅与可靠性、保障性有关［9］。

导弹武器装备为可修复产品，根据其使用特点，更应该关注其贮存可用性，因为贮存可用性反映了导弹武器装备一旦需要就能立即投入使用的能力［10］。

对处于贮存状态的导弹武器装备而言，从贮存状态转入使用状态时，需进行装备装配、调校、检测、加注燃料等工作，而这些工作均有明确的技术要求和操作规范，且操作人员均为经过专业培训的专业技术人员，故由于这些因素导致装备不可用的概率Psw很小，则装备的贮存可用度Azc与贮存可靠度Rzc之间存在如下关系:

在不进行检测、修复的情形下，贮存可用度的变化趋势和规律与贮存可靠度保持一致。根据“浴盆曲线”原理，处于贮存期内的装备，其故障率基本不变，可靠度函数为指数函数形式，故贮存过程中可用度函数也呈指数函数形式。

2.2 贮存可用度模型

为确保导弹武器装备贮存过程中的贮存可用度，就需要对其进行定期检测。检测过程中若发现故障，需要及时进行修复，使可用度得到提高，然后重新以指数函数形式下降。

需要说明的是，虽然进行检测、修复能使可用度得到提高，但受故障检测率、维修率、修复时间等因素的影响，可靠度不可能恢复到1，可用度不可能恢复到(1－Psw)。所以，如果根据“第1 次达到最低贮存可用度”来确定检测周期，后续贮存过程中的最低贮存可用度便得不到保证。

贮存可用度的变化(从第2 次检测开始)是一种周期性变化。每次检测前，贮存可用度降低到最低值(根据战备需要确定)，进行检测、修复后，可用度得到提高，然后重新以指数函数形式下降，在下一次检测前达到最低值。贮存可用度的变化趋势和规律如图1 所示。

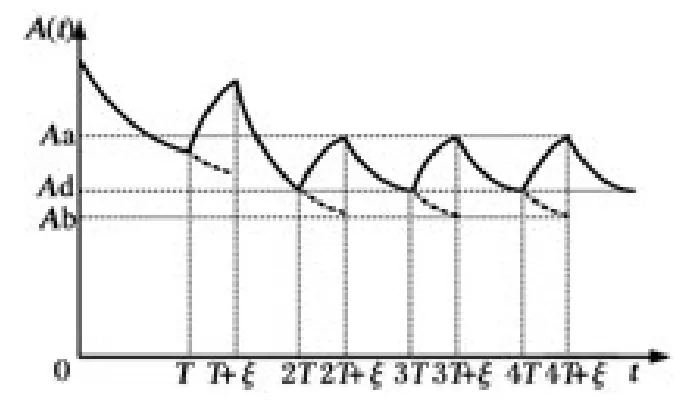
图1 贮存可用度变化趋势和规律

图1 中，Ad为确保装备满足战备需要所要求的最低贮存可用度;T 为检测周期;ξ 为修复时间;Aa为进行检测修复情形下达到(kT +ξ)(k =2，3，4，…)时的贮存可用度;Ab为kT(k =2，3，4，…)时检测合格的产品达到(kT +ξ)(k =2，3，4，…)时的贮存可用度。

设在第k(k =2，3，4，…)次定期检测前，装备的贮存可用度达到Ad;检测时的故障检测率为γ;维修率为μ;考虑到维修时间、保障资源、管理体制等因素，可用于修复的最长时间为ξ;且ξ 时间内的维修度为M，则对于该批产品而言，由于检测、修复而提高的可用度为

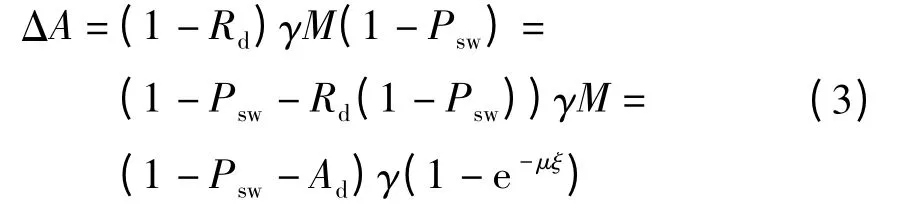
对于该批产品而言，此次检测时合格的产品经过ξ 时间后，贮存可用度为

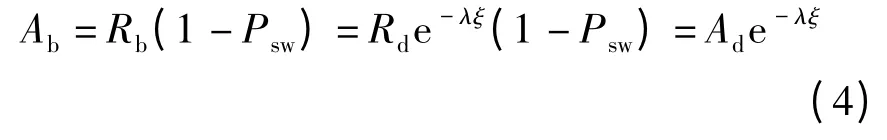
则对于该批产品而言，此次检测并进行修复后，贮存可用度为

贮存可用度从Aa开始，重新以指数函数形式下降，至下一个检测周期时(经历时间为t =T－ξ)，达到Ad，即

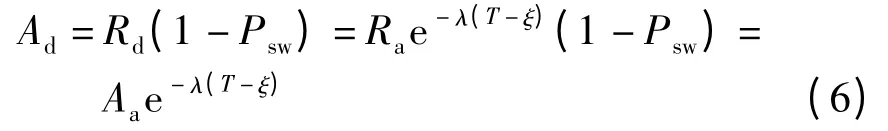
综合式(3)～(6)，得到贮存可用度与检测周期之间的数学关系模型如下:

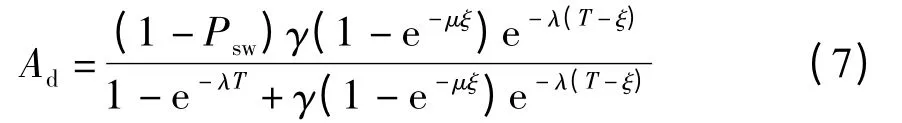
2.3 贮存过程中检测周期确定方法

工程实践中，常根据战备需要提出一个最低贮存可用度，这时，就可根据上文建立的数学模型，求得对应于最低贮存可用度的检测周期。

根据式(7)，得

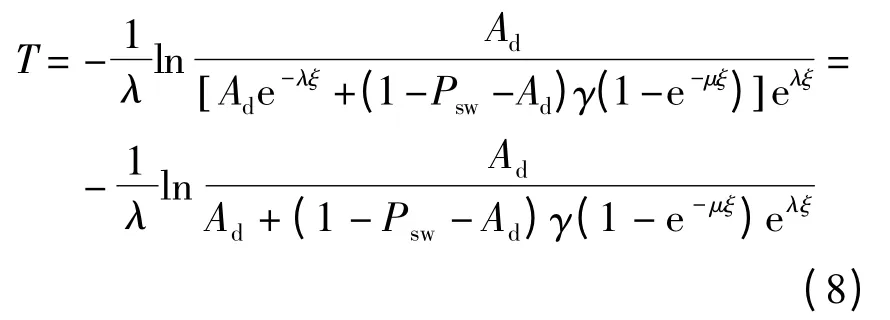
根据此模型，也可求得确保最低贮存可用度的第一次检测时间t1满足:

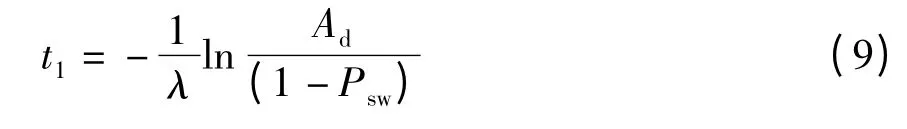
3 应用实例

以某型空空导弹武器装备为例，该导弹以全弹形式贮存，检测合格后，仅需进行简单的结构件装配即可投入使用。装配工作有明确的操作规范，且操作人员为经过专业培训的专业技术人员，故由于装配等因素导致导弹不可用的概率很小，可设为Psw=0.01。

根据该型导弹研制过程中开展的设计分析与试验验证工作，并根据类似产品的实际使用经验，可得:贮存状态失效率λ =9.919 4 ×10－6;库房所用检测设备的故障检测率γ =95%;维修率μ =1/240 =0.004 2;考虑到维修时间、保障资源、管理体制等因素，装备管理体制规定的可用于修复的最长时间ξ=15 d=360 h。

将上述数据代入式(8)～(9)，可得对应于最低贮存可用度的检测周期和第一次检测时间，如表1 所示。

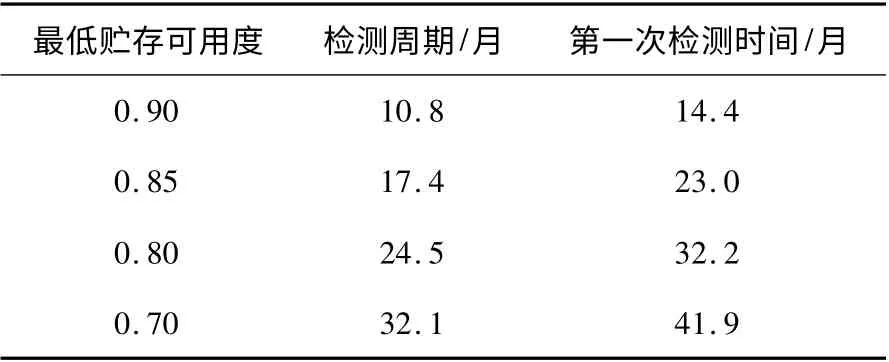
表1 最低贮存可用度对应检测周期和第一次检测时间

该型导弹在实际贮存过程中，检测周期为18个月。根据对用户的实际调研分析结果，每18个月检测一次基本能够保证85%以上的导弹合格可用，与本方法确定的检测周期基本一致，表明该方法是合理可行的。

4 结 论

本文建立的贮存可用度与检测周期之间的数学模型充分考虑了导弹武器装备的实际贮存过程，综合了可靠性、维修性、测试性、保障性等因素，能够有效利用导弹研制过程中的设计与试验数据来求得检测周期，改进了主要根据可靠性信息和类似产品使用经验来确定检测周期的不足之处。结合某型导弹的相关数据所开展的应用结果与实际调研分析结果基本一致，表明该方法具有工程实践应用价值，可以为确定导弹武器装备的检测周期提供参考。

［1］张金春，刘超. 定期检测对导弹武器系统贮存可靠性的影响分析［J］. 战术导弹技术，2008(1):44－48.

［2］王宇翔，王国华，袁洪. 定检对导弹引信系统可靠性的影响分析［J］. 电子产品可靠性与环境试验，2003(4):13－15.

［3］李光辉，赵磊. 基于Weibull 分布的定期检测贮存系统的可靠性模型［J］. 鲁东大学学报(自然科学版)，2012，28(3):219－222.

［4］徐廷学. 基于定期检测的导弹贮存可靠性研究［J］.弹箭与制导学报，2008，28(1):248－250.

［5］孙亮，徐廷学，代莹.基于定期检测的导弹贮存可靠性预测模型［J］. 战术导弹技术，2004(4):16－19.

［6］张永进，赵明. 基于定期检测的贮存可靠性模型及其参数估计［J］. 系统工程理论与实践，2008(10):82－88.

［7］熊海林，沈永福，邓方林，等. 库存导弹定期检测模型的数字仿真研究［J］. 系统仿真学报，2000，12(3):219－221.

［8］李志强，王茜，张孝虎，等. 空空导弹PHM 系统总体设计研究［J］. 航空兵器，2014(5):55－59.

［9］王自力. 可靠性维修性保障性要求论证［M］. 北京:国防工业出版社，2011.

［10］顾辉，宋笔锋. 地空导弹武器系统可用性评估［J］.火力与指挥控制，2010，35(6):50－52.