基于Hilbert-Huang变换的1 000kV输电线路雷电绕击与反击识别方法

罗日成 李 稳 陆 毅 黄 彪 胡宗宇

（1. 长沙理工大学电气与信息工程学院 长沙 410004 2. 国电永福发电有限公司 桂林 541805 3. 国网岳阳供电公司 岳阳 414000 4. 国网益阳供电公司 益阳 413000）

1 引言

前苏联和日本为了防护雷电过电压，都对特高压架空输电线路作了精心的防雷设计。尽管国外在特高压线路设计时认为特高压架空输电线路耐雷水平很高，但运行后仍多次发生雷击跳闸事故[1]。前苏联1 150kV特高压线路在6年的运行时间内发生雷击跳闸 21次，跳闸率高达 0.7次/（km·a）。特高压输电线路一般长达数百公里，由于受到输电走廊的地形、气候等因素的影响，极易遭受雷击，从而产生过电压，造成绝缘子闪络，引起跳闸停电[2]。研究表明，雷击是造成输电线路跳闸的主要原因，它又分为绕击和反击两种[3,4]。绕击和反击的机理及过程不同，防护措施也不同。若对线路雷击方式进行有效识别，就能给线路安全运行及防雷工作提供正确的指导，给防雷措施的制定提供理论依据。

先导发展法从气体放电的物理过程出发，先导的发展速度与加在绝缘子串两端的瞬时电压和先导发展长度有关，通过计算先导发展长度来判断是否闪络，理论上适用于任何波形，能直观、合理地描述绝缘击穿过程[5]。同时，研究发现对于500kV及以上的输电线路，由于杆塔高度的增加，雷电波在杆塔及线路中的折、反射作用对于杆塔节点电位变化的影响很大，且最终影响线路雷电过电压[6-8]，所以将先导发展模型应用于输电线路雷电绕击与反击的识别，更符合实际情况，且克服了电气几何模型对识别结果的影响。

本文首先在考虑雷电先导发展过程的基础上，利用ATP-EMTP软件建立了1 000kV输电线路雷电绕击与反击的仿真模型，然后运用Matlab软件对仿真数据进行分析，采用HHT方法来提取特高压线路中雷电过电压信号的特征量，并计算其方差贡献率，以此判断绕击与反击。本文首次将希尔伯特-黄变换应用于特高压输电线路雷电绕击与反击识别，克服了傅里叶算法和Prony算法难以处理非平稳信号的缺点，并规避了小波算法中小波基难以选取的问题[9]，能够从非平稳的高频振荡信号中准确提取动态振荡特性以及丰富的系统故障暂态信息。实测技术中采用磁带、磁钢棒等方法通过测量雷电流波形参数来进行绕击与反击的识别，由于此类装置不能重复测量，数据获取工作量大，依靠工作经验来判别，容易出现误判[9]。本文所提出的雷电绕击与反击识别方法只需通过变电站录波装置记录的雷电过电压信号即可对雷击方式进行准确识别。仿真及实测数据验证结果表明：本文方法能为1 000kV输电线路防雷的分析和设计提供理论参考。

2 输电线路雷电暂态仿真模型

2.1 先导法模型

先导发展是长间隙放电的特有现象，本文用非线性电感模型模拟雷电先导发展的长间隙放电。它是一种高精度、长间隙放电的先导法模型，能够模拟放电前驱电流的发展过程。非线性电感模型依据外加电压到达间隙的临界放电电压为先导开始条件，只要放电时间不是特别短，先导开始时间对模拟精度的影响不大。非线性电感模型的电路如图 1所示[11]。

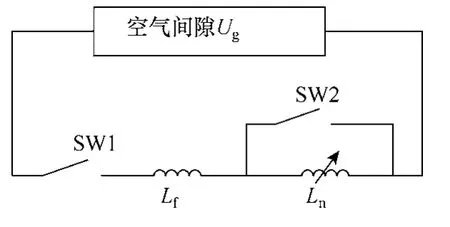
图1 先导发展的非线性电感模型Fig.1 Nonlinear inductance model

图 1中，Ln是放电间隙的等值非线性电感，以φn-i的形式给出其值。Lf表示闪络后稳态电弧的等值线性电感。SW1表示先导发展开始的开关，当间隙电压达到先导开始电压Vm时闭合。SW2表示闪络的开关，当间隙电流达到闪络电流if时或者间隙电压为零时闭合。上述相关参数的计算方法[11]为

式中，D为间隙长，m；L0为小电流领域的等值电感；n为大电流领域的等值电感-电流特性的斜率；I0为等值电感为L02n时的电流，即拐点电流；Vm为先导开始电压；if为闪络电流。

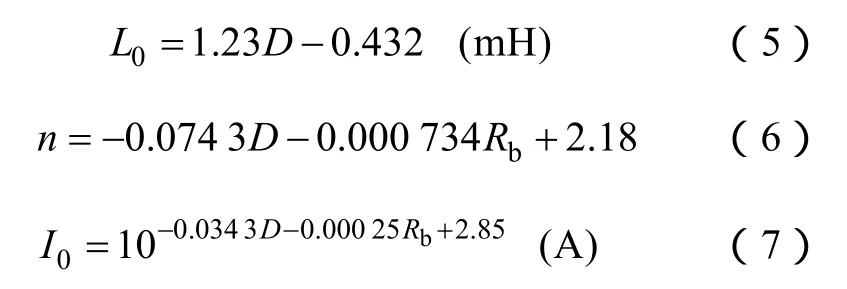
式中，Rb是从间隙等效得到的系统等值阻抗，可在闪络点插入 1A电流源后计算得到，也可取 100～300Ω范围内的值，此值对计算结果的影响不大。式（1）～式（7）中相关参数的取值和适用条件，读者可参阅文献[11]，此处不再赘述。

2.2 铁塔模型

1994年Yamada和Ishii[12]用直测法对特高压塔进行了测量，提出了基于EMTP的多层传输塔模型。将铁塔分成四段，用无损线路和R-L并联电路的串接来模拟铁塔，Rf为塔脚接地电阻，如图 2所示。

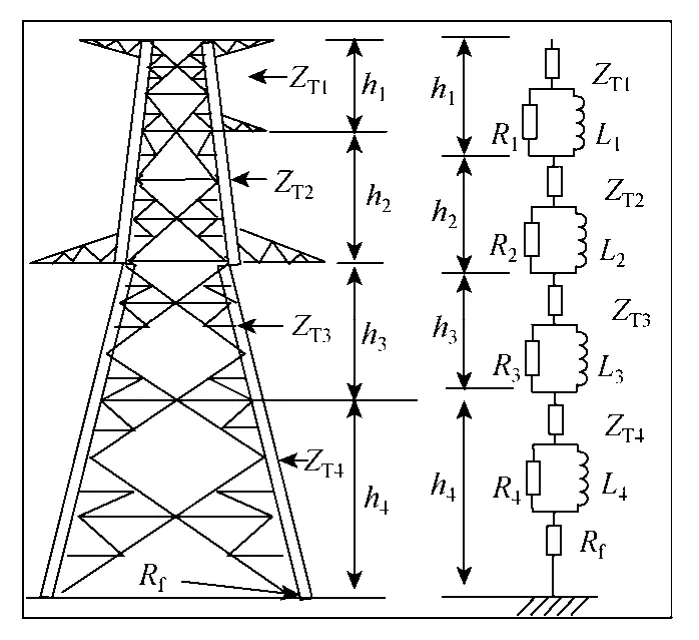
图2 多层传输塔模型Fig.2 Multistory transmission tower model

铁塔分段模型中各段中的阻尼电阻Ri和阻尼电感Li根据文献[12]中给出的公式来计算。

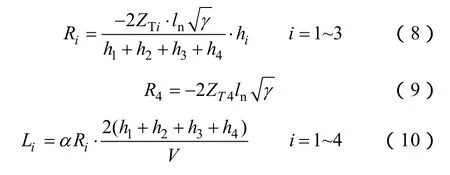
式中，hi各段相应的长度；ZTi为铁塔波阻抗；γ为铁塔整体的衰减系数；V为冲击波在铁塔中的传播速度；α为阻尼系数。文中参数取值按文献[12]：ZTi=120Ω（i=1～4），γ=0.7，V=300m/μs，α=1。

3 输电线路的雷电过电压电磁暂态仿真

3.1 仿真条件

利用ATP-EMTP以1 000kV线路为例，建立了考虑先导发展的过程仿真模型，研究雷电绕击与反击的暂态特性。仿真中雷电流模型为2.6/50μs的双指数波；根据 DL/T620—1997，文中雷电流对应的雷电通道波阻抗取400Ω；绝缘子串采用考虑先导发展的非线性电感模型；杆塔采用多层传输塔模型，接地电阻为10Ω；线路采用JMarti·模型且考虑了冲击电晕的影响[13]。仿真模型如图3所示。

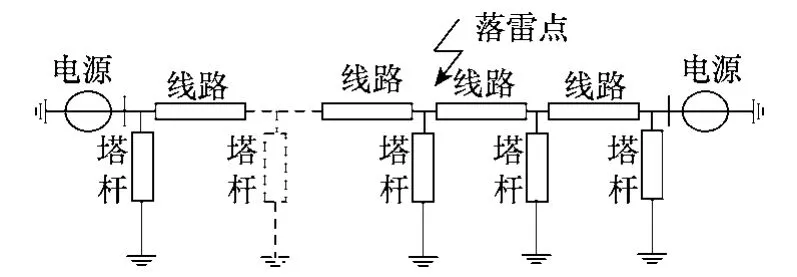
图3 输电线路模型Fig.3 Transmission line model

3.2 先导发展对雷电过电压的影响

基于本文所搭建的考虑了先导发展的雷电过电压仿真模型，研究反击时先导发展对线路过电压的影响。仿真结果如图4所示。

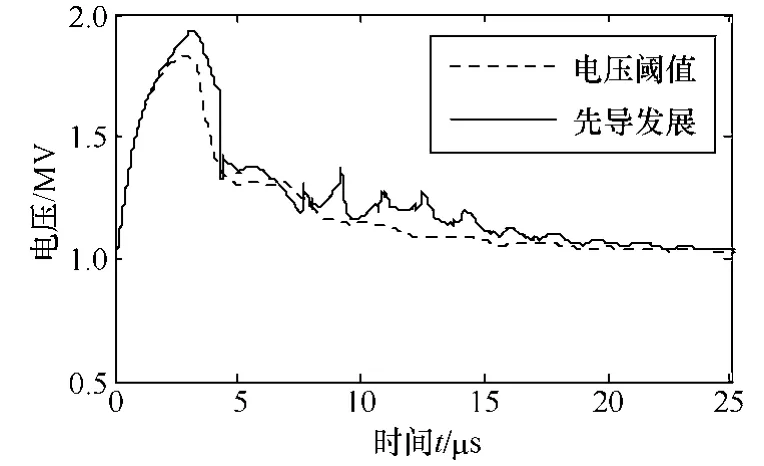
图4 线路电压仿真波形Fig.4 Simulation waveforms of voltage on transmission line

图4中虚线表示没有考虑先导发展（电压阈值模型）的过电压波形，实线表示考虑了先导发展仿真得到的线路过电压波形。从图4中可以看出实线与虚线相比，幅值更大、波头更陡、电压上升速度更快且波头过后的时间内振荡幅度更大，衰减慢。由此可见，采用先导法的线路过电压波形的波头更陡、振荡持续时间更长，这是因为先导法考虑了雷电波在杆塔及输电线路中的折、反射以及工频电压叠加的影响，也更符合实际情况[14]。因此，在研究输电线路绕击与反击识别时，考虑先导的发展对线路雷击过电压的影响，将更加接近实际的物理过程。

本文分别以雷击A相线路和杆塔顶部进行雷电绕击与反击仿真分析，相应的雷电过电压波形分别如图5和图6所示。从图5和图6的仿真波形可以看出，考虑先导发展的雷电绕击与反击波形具有波头陡、幅值大的特点，并且非闪络相和闪络相电压都发生了高频振荡，实际过电压录波中很难从波形图上直观地判断雷击类型。为了能够对输电线路的绕击与反击进行快速且准确的识别，本文通过提取过电压信号中的特征量进一步区分雷击类型。

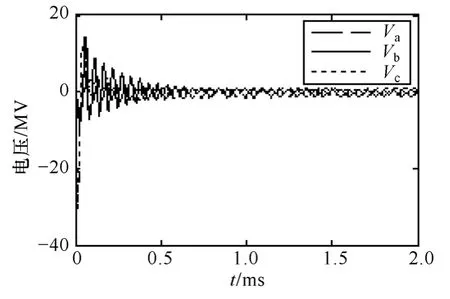
图5 绕击过电压波形Fig.5 Shielding failure overvoltage

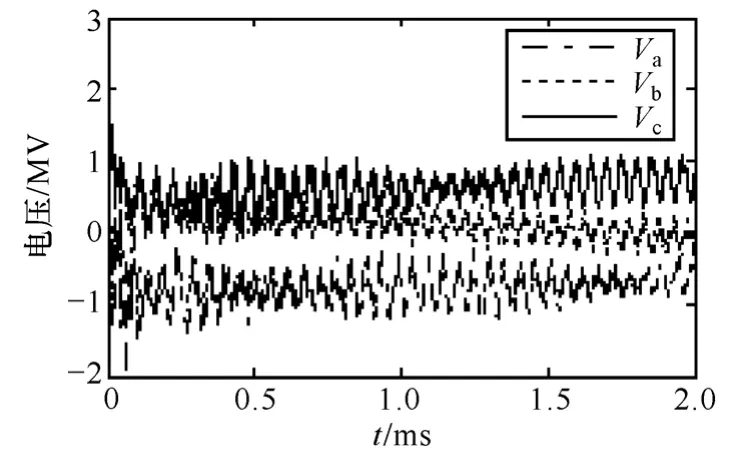
图6 反击过电压波形Fig.6 Back striking overvoltage

4 输电线路雷电过电压识别判据

Hilbert-Huang（HHT）方法是黄锷根据近代知名数学家 Hilbert的数学理论而提出的。HHT方法由两部分组成：经验模式分解（Empirical Mode Decomposition，EMD）和Hilbert变换。HHT方法具有良好的自适应性、快速性，非常适合对非平稳、非线性信号的分析[9,15]。

4.1 固有模式函数（Intrinsic Mode Function，IMF）

事实上，定义一个有意义的瞬时频率要求函数关于局部零平均值对称，并且过零点和极值点数量相同。因此提出了IMF的定义[16]：

（1）整个数据范围内，极值点的数量与过零点的数量必须相等或相差一个。

（2）在任意点处，所有极大值点形成的包络线和所有极小值点形成的包络线的平均值为零。

4.2 经验模式分解EMD

Hilbert变换不能对一个任意信号的频率内容做完整分析，是由于多数信号不是IMF，在任意时刻，信号可能包含多个频率模式，因此对一个信号的频率特性进行完整分析时，需首先对该信号进行 EMD分解，得到IMF。EMD分解可形象地描述为“筛选”过程[16,17]，步骤如下：

（1）提取原始信号所有的极大值和极小值；然后用三次样条函数曲线分别将所有的局部极大值点和极小值点进行连接，形成上、下包络线。上、下包络线之间应包含所有的原始信号数据。设上、下包络线的均值函数为m1，计算原始信号x(t)与包络均值函数m1的差值函数，记为h1。

（2）一般情况下，h1不是一个IMF，需要加以平滑化。用h1代替x(t)，重复步骤（1），直到得到一个满足IMF条件的函数，记为c1，则c1为原始信号x(t)的第一个满足固有模式函数条件的分量。

（3）将c1从原始信号x(t)中分离出来，得到残余项，记为r1

然后将r1作为“原始信号”，重复步骤（1）和（2），得到第2个满足固有模式函数的分量，并记为c2。反复循环步骤（1）～（3），则可以求出原始信号x(t)的第n个满足固有模式函数的分量。则有

（4）rn变成单调函数时，原始信号x(t)分解结束，可以得到EMD的分解结果为

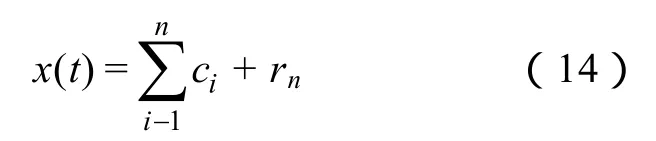
式中，rn称为残余函数。

信号经过 EMD分解后，得到一系列平稳的时域信号，这些时域信号的频率依次降低，其中c1包含了原始信号中的最高频率成分，c2次之，而rn是包含频率最低的成分[18]。

4.3 希尔伯特谱分析

EMD分解结束后就得到了所有IMF，对第i阶固有模式分量ci(t)进行Hilbert变换

以ci(t)为实部、(t)为虚部构造解析信号

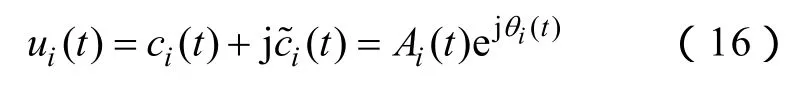
其中

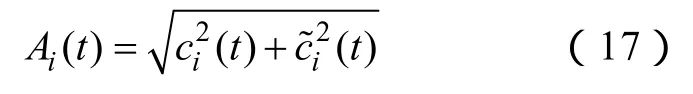
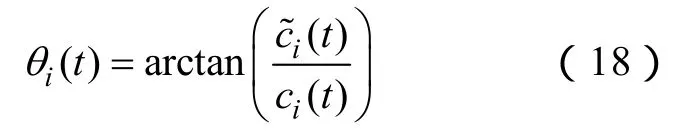
瞬时频率为

则原始信号x(t)可以表示为

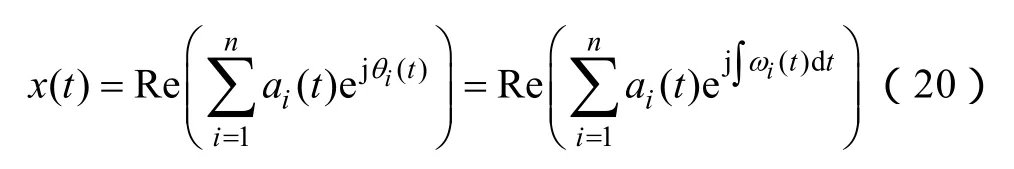
这里，没有考虑余项rn，因为它只是单调函数或常量，Re表示取实部运算。由希尔伯特变换得出的振幅和频率都是时间的函数，将这种振幅的频率-时间分布定义为Hilbert幅值谱(,)Htω，简称Hilbert谱，记作

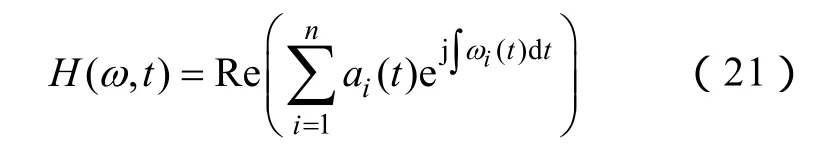
如用三维图形表达幅值、频率和时间之间的关系，可以把振幅用灰度的形式显示在频率-时间平面上。

4.4 过电压信号的HHT分析及特征量提取

由 3.2节可知，雷电过电压波形振荡频率高且包含大量的谐波，而且暂态过程中的特征频率分量不固定，是一种典型的非平稳信号。因此，利用HHT对于非平稳信号分析非常适合的特点，将HHT运用在特高压线路的雷击过电压信号分析和处理中是可行的。文章以雷击线路A相为例，运用HHT方法对线路雷电绕击与反击过电压信号进行特征量提取和绕、反击识别。具体分析步骤如下，对应的流程如图7所示。

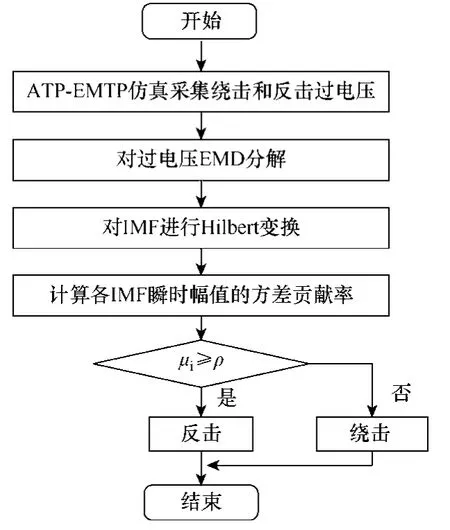
图7 绕击与反击识别系统流程图Fig.7 Identification flowchart of shielding failure and backing striking

（1）利用ATP-EMTP软件仿真分析，获得绕击与反击产生的过电压波形。

（2）对绕击与反击过电压进行 EMD分解，得到若干阶相应的IMF。绕击与反击过电压信号对应的EMD分解结果分别如图8和图9所示。

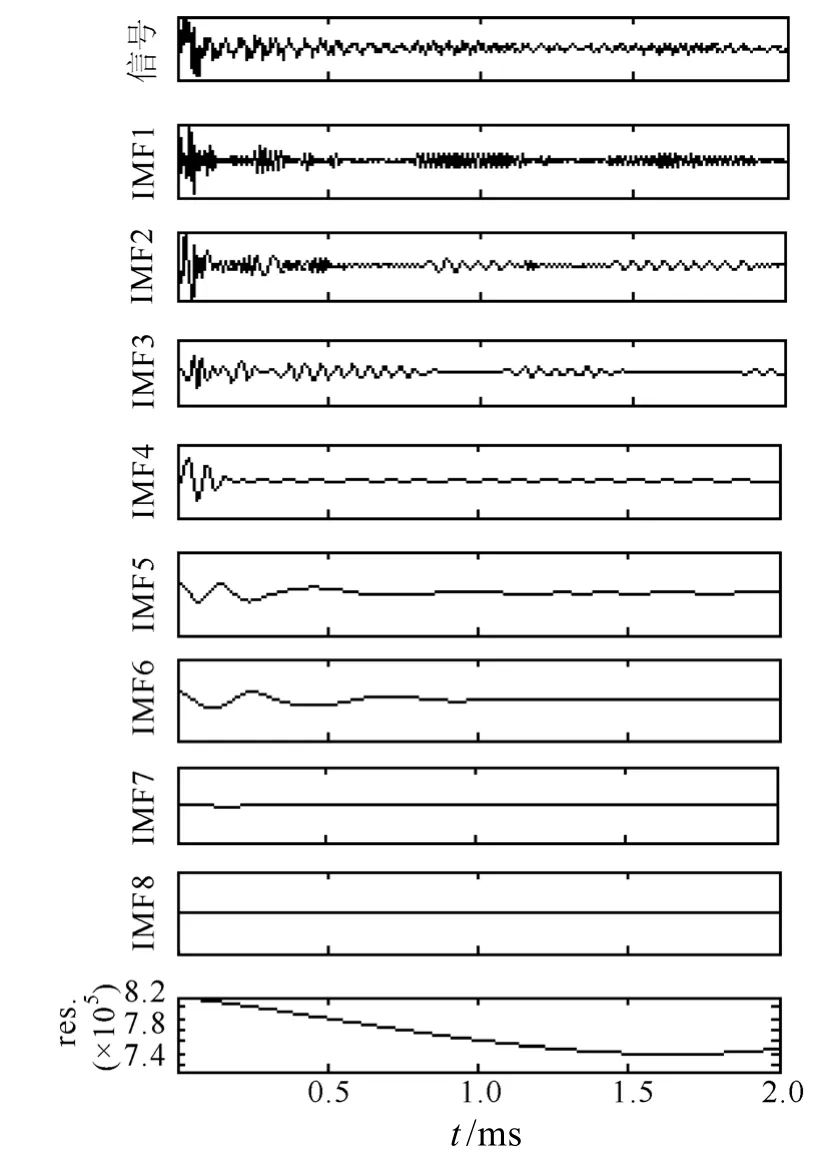
图8 绕击过电压的EMD分解Fig.8 EMD decomposition of shielding failure overvoltage

图9 反击过电压的EMD分解Fig.9 EMD decomposition of back striking overvoltage

（3）EMD分解得到若干阶 IMF后，对前四阶IMF进行Hilbert变换，得到其瞬时幅值。

（4）计算各IMF瞬时幅值的方差贡献率。方差贡献率表示第i个元素的方差在全部方差中所占的百分比，能够描述第i个元素综合信息的能力大小；方差分量（Variance Component）贡献率大，说明在这个事件中（100%）所占内容多，为主效应。

方差贡献率为

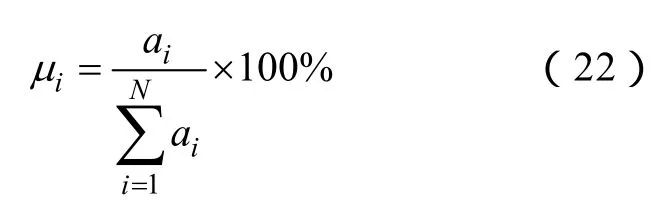
（5）把计算所得任意IMF瞬时幅值的μi的值与阈值ρ比较，若μi≥ρ即为反击，否则为绕击。此处μi为对应的前四阶IMF瞬时幅值的方差贡献率，ρ为判据门限值，根据经验设定。

EMD过程即是将原始信号按照不同尺度的波动或趋势逐级分解成若干个IMF，因为绕、反击过电压信号中包含的故障信息不一样，所以分解得到的IMF和其阶数都不同。根据图8和图9可以看出，阶数越靠前的IMF的频率越高，振荡越明显且振荡随着时间逐渐减弱，这与图5和图6中的A相电压随时间变化的趋势是一致的。频率较高的前几阶IMF包含了原始信号中最显著、最重要的信息，这是由IMF信号的本性所决定的，它们能比较全面地反映出原始信号的特征，因此本文选取前四阶IMF来进行分析和特征量的提取。将前四阶 IMF经过Hilbert变换后得到其对应的IMF瞬时幅值，分别如图10和图11所示。

图10 绕击过电压IMF的瞬时幅值Fig.10 Instantaneous amplitude of the shielding failure overvoltage’s IMF

图11 反击过电压IMF的瞬时幅值Fig.11 Instantaneous amplitude of the back striking overvoltage’s IMF

从图10和图11可以看出，当线路雷击闪络后幅值迅速增大且大幅振荡，这与ATP-EMTP仿真结果是相符合的。该幅值谱较IMF比较而言，能够更准确地反映原始信号的内部特性，可用来检测突变信号，因此选取 Hilbert变换得到的前四阶 IMF的瞬时幅值作为特征量，并以计算其方差贡献率μi。方差贡献率的差异不仅描述了该瞬时幅值谱对应的IMF表达信息的能力大小，而且也反映了原始信号的内部特征的区别。因此，选取μi作为识别的判据能够对绕、反击进行有效区分。

绕、反击时的IMF瞬时幅值的方差贡献率分别如图12和图13所示。从图12和图13中可知，绕击时，前四阶IMF瞬时幅值的方差贡献率比较均衡且都在40%以下。而反击时则IMF1分量占主要部分，μ1=49.582%，其他分量的方差贡献率比较均衡且占的比重比较小。根据方差贡献率整体分布的特点，将μi与设定的判据门限值ρ比较用来进行绕、反击的识别。

图12 绕击时IMF瞬时幅值方差贡献率Fig.12 Variance contribution rate of the shielding failure instantaneous amplitude IMF component

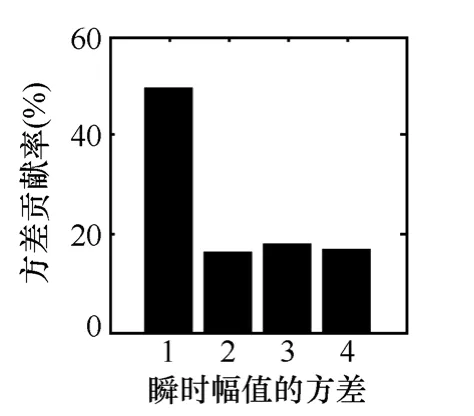
图13 反击时IMF瞬时幅值方差贡献率Fig.13 Variance contribution rate of the back striking instantaneous amplitude IMF component

5 绕击与反击识别方法的验证

在前文理论分析的基础上，通过改变杆塔接地电阻的大小和雷电流幅值，对本文方法进行了验证分析，分析结果见表1。根据表1可知，绕击时任意方差贡献率都小于40%，且比重相差不大。反击时μ1＞40%且占主要部分，其他剩余分量所占比例均匀，与μ1相比相差较大，故本文将ρ设定为40%。由表1数据分析可知，不同参数条件下，绕击（反击）过电压的各 IMF瞬时幅值的方差贡献率分布趋势基本相同，改变接地电阻和雷电流幅值对判据没有影响，可对线路绕击与反击做出正确的识别。因此该方法能有效地实现雷电绕、反击方式的识别。

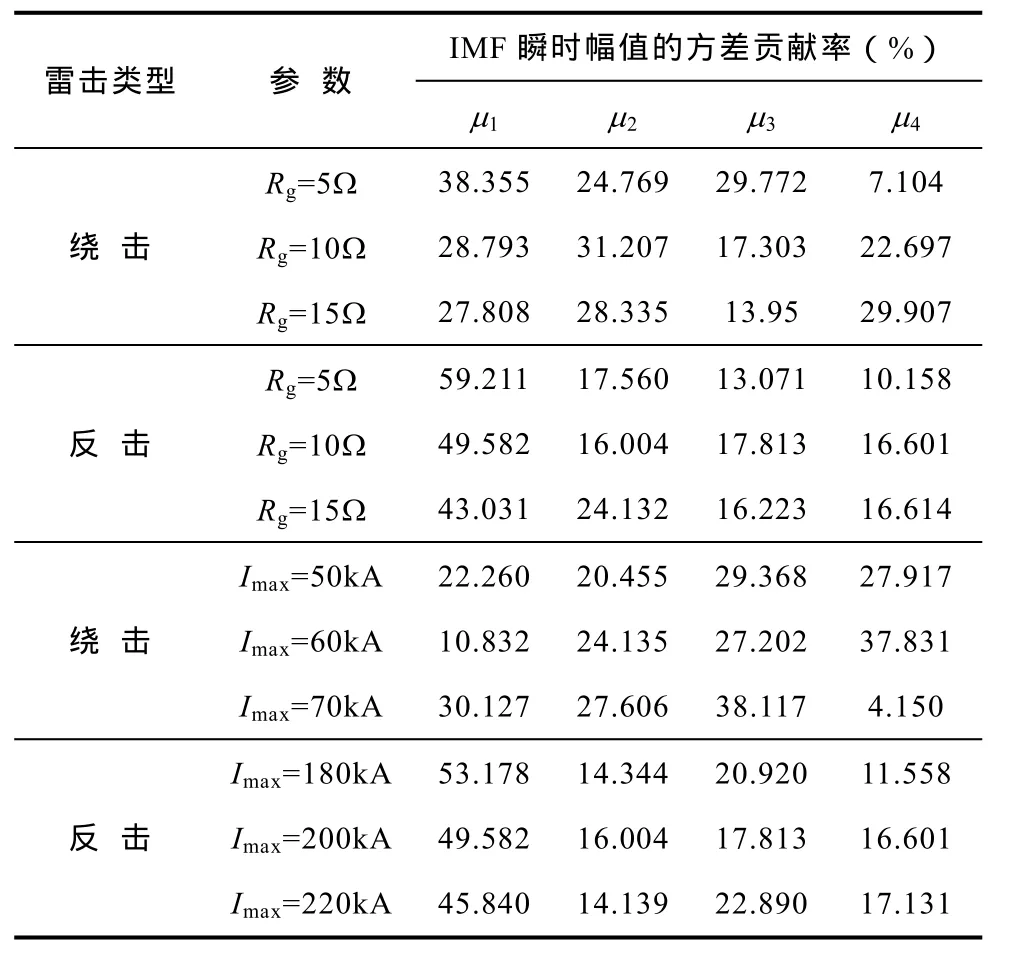
表1 绕击与反击特征参数Tab.1 Characteristic parameters of shielding failure and back striking overvoltage

为了验证本文设计的雷电绕击与反击识别新方法在实际电网运行中是否可行，根据某多雷地区一变电站实际运行数据，运用本文所提出的识别方法进行验证分析（受篇幅限制，略去详细的验证过程）。原始信号在没有进行去噪的情况下进行验证，结果见表2，绕击和反击识别率分别达到88.2%和92.3%，能达到预期效果。

表2 近3年线路运行雷击记录及识别结果Tab.2 The lightning records of line running nearly three years and recognition results

6 结论

（1）在研究特高压交流输电线路发生雷电绕击与反击时，本文考虑了雷电先导发展对雷击暂态过程的影响。研究结果表明，考虑先导发展的线路过电压波形具有以下特征：①线路雷击过电压波的波头幅值明显比采用电压阈值模型的高，而上升速度更快；②雷击过电压波的陡度更高且在线路上衰减更慢，振荡持续时间更长。以上研究结论更加接近雷击线路时激发的线路过电压波形的实际情况。

（2）本文运用HHT方法提取了特高压线路雷电绕、反击过电压信号中高频暂态信息，实现了线路雷电绕击、反击的有效识别。首先对绕击、反击过电压波形进行 EMD分解，将分解后信号的前四阶IMF进行Hilbert变换，把计算得到的瞬时幅值作为特征量，然后计算特征量所对应的方差贡献率，将方差贡献率作为绕击与反击的识别判据，实现雷击绕击、反击的识别。仿真结果和变电站实测数据的分析表明该方法能够正确有效地实现输电线路绕击与反击的识别，且不受线路接地电阻和雷电流幅值的影响，具有较高的识别正确率。

[1] 维列夏金,吴维韩. 俄罗斯超高压和特高压输电线路防雷运行经验分析[J]. 高电压技术,1998,24( 2):76-79.

Weilie Xiajin,Wu Weihan. The analysis of lightning protection for EHV and UHV transmission line in Russia[J]. High Voltage Engineering,1998,24(2):76-79.

[2] 刘振亚. 特高压直流输电技术研究成果专辑[M].北京: 中国电力出版社,2006.

[3] 邹贵彬,高厚磊,朱峰,等. 输电线路雷击与故障的积分识别方法[J]. 电力系统保护与控制,2012,40(9): 43-48.

Zou Guibin,Gao Houlei,Zhu Feng,et al. Integral identification method of lightning stroke and fault for transmission line[J]. Power System Protection and Control,2012,40(9): 43-48.

[4] 李瑞芳,吴广宁,曹晓斌,等. 输电线路雷电绕击率的三维计算方法[J]. 电工技术学报,2009,24(10):134-138.

Li Ruifang,Wu Guangning,Cao Xiaobin,et al. Threedimensional calculation method on shielding failure rate of transmission lines[J]. Transactions of China Electrotechnical Society,2009,24(10): 134-138

[5] 曾嵘,耿屹楠,李雨,等. 高压输电线路先导发展绕击分析模型研究[J]. 高电压技术,2008,34(10):2041-2046.

Zeng Rong,Geng Yinan,Li Yu,et al. Lightning shielding failure model of transmission line based on leader progress model[J]. High Voltage Engineering,2008,34(10): 2041-2046.

[6] 肖萍,汪沨,黄福勇,等. 基于连续先导的线路绝缘闪络判据的研究[J]. 电网技术,2012,36(11):271-276.

Xiao Ping,Wang Feng,Huang Fuyong,et al. Research on criterion for line insulation flashover based on development of continuous leader[J]. Power System Technology,2012,36(11): 271-276.

[7] Taniguchi S,Okabe S,Takahashi T,et al. Discharge characteristics of 5m long air gap under foggy conditions with lightning shielding of transmission line[J].IEEE Transactions on Dielectrics and Electrical Insulation,2008,15(4): 1031-1037.

[8] 陈仕龙,束洪春,谢静,等. 特高压直流输电线路故障暂态信号高频特性研究[J]. 电力系统保护与控制,2012,40(21): 84-89.

Chen Shilong,Shu Hongchun,Xie Jing,et al. High frequency characteristic analysis of fault transient signal at UHVDC transmission lines fault[J]. Power System Protection and Control,2012,40(21): 84-89.

[9] 齐冲. 高压输电线路雷电绕击和反击的识别[D]. 南宁: 广西大学,2007.

[10] 翟进乾. 配电线路在线故障识别与诊断方法研究[D]. 重庆: 重庆大学,2012.

[11] 吴文辉,曹祥麟. 电力系统电磁暂态计算与 EMTP应用[M]. 北京: 中国水利水电出版社,2012.

[12] Yamada T,Mochiznki A. Experimental evaluation of a LTHV tower model for lightning surge analysis[J].IEEE Transactions on Power Delivery,1999,10(1):630-635.

[13] Yang Pengcheng,Chen Shuiming,He Jinliang,et al.Lightning impulse corona characteristic of 1 000kV UHV transmission lines and its influences on lightning overvoltage analysis results[J]. IEEE Transactions on Power Delivery,2013,28(4): 2518-2525.

[14] Taniguchi S,Okabe S,Asakawa A,et al. Flashover characteristics of long air gaps with negative switching impulses[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2008,15(2): 399-406.

[15] 刘毅力,陶学军,李佳,等. 基于 HHT的风力发电机组滚动轴承故障特征提取[J]. 电力系统保护与控制,2012,40(20): 79-82,88.

Liu Yili,Tao Xuejun,Li Jia,et al. Feature extraction of rolling bearing for wind generator based on HHT[J].Power System Protection and Control,2012,40(20):79-82,88.

[16] Gu F C,Chang H C,Chen F H,et al. Application of the Hilbert-Huang transform with fractal feature enhancement on partial discharge recognition of power cable joints[J]. Science,Measurement & Technology,2012,6(6): 440-448.

[17] Huang N E,Shen Z,Long S R. A new view of nonlinear water waves: The Hilbert spectrum[J]. Annual Review of Fluid Mechanics,1999,31: 417-457.

[18] 公茂法,夏文华,李国亮,等. 变压器和应涌流和励磁涌流识别新判据[J]. 电力系统保护与控制,2012,40(18): 139-143.

Gong Maofa,Xia Wenhua,Li Guoliang,et al. New judgment to identify sympathetic inrush and inrush current[J]. Power System Protection and Control,2012,40(18): 139-143.