让“好题”照亮学路

叶柱

叶  柱 中学高级教师，浙江省绍兴市上虞区教学研究室小学数学教研员，全国人教版课改实验优秀教师，浙江省特级教师，浙江省教育学会小学数学分会学术委员，浙江省中小学教材学科审查委员会委员，浙江省绍兴市名师培养工程导师，绍兴市学科带头人，绍兴市十佳青年教师标兵，绍兴市教科研先进个人。

自1994年参加工作以来，潜心课堂，钟情教研。曾获“浙江省第十届小学数学优质课评比”一等奖、“华东六省一市第十届小学数学优质课评比”一等奖、“中国教育学会小学数学教学专业委员会第十二届优秀论文评选”一等奖。150余篇学术论文公开发表，个人专著《数学教学新视界探真》由浙江大学出版社正式出版，主编或参编教学用书近百万字。

无论哪个学段，题目始终是数学学习的重要资源。学生在“例题”的研探中体验、在“习题”的操练中内化、在“试题”的测评中反思，从而夯实了学科基础、领会了数学思想、积累了学习经验。波利亚曾经强调：“一个专心的认真备课的教师，能够拿出一个有意义但不复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一扇门，把学生引入一个完整的理论领域。”确实，题目品质的优劣直接影响着学习效果的好坏。作为一名数学教师，理应多给学生提供“有意义但不复杂”的“好题”，为其数学建构提供绝佳的载体、打开宽绰的空间。下面，笔者就新理念下小学数学“好题”的基本属性谈些思考。

一、“好题”，是有情趣的

数学题应有情趣，其道理是显而易见的。正如《义务教育数学课程标准》（2011年版）所指出的：“课程内容的选择要贴近学生实际。”数学题的设计也要贴近学生“未成年状态”的实际，力求顺应童真、趣味盎然。但是，有一种现象亟须引起警惕。有些教师为了追求情趣性，在题目旁边配上一些诸如“孙悟空”的卡通形象，就美其名曰“让我们和孙悟空一起解决问题”，而具体的题目信息及解答过程则与孙悟空毫不沾边。在这里，数学题的情趣性被狭隘地理解为“装饰”与“噱头”。由此，会使学生受到浅层刺激的外部干扰，从而影响主体思考的精度和深度。所以说，“好题”的情趣，绝不等于“加点花头”“弄点幌子”，而是通过营造贴近儿童心理的问题情境，将需要落实的目标点以学生喜闻乐见的生动方式呈现出来，激发学生“亲近题目”的热情与“一探究竟”的欲求。

例如，全国各版本数学教材编写时都强调“对话”形式，即通过人物之间的交流分享，生成问题，提炼策略，明晰知识。“对话”是人们参与现实生活的重要方式，也吻合学生乐于表现的年龄特点。为此，我们可以借鉴教材的编写特点，设计“对话”形式的数学题，为解决问题预设一条“抽丝剥茧”的探究之路，由此凸显题目的内涵与情趣。

【题例1】“除数是一位数的口算除法”原创题（人教版三年级下册）

三位小朋友同时在口算一道“除数是一位数的除法题”。根据他们的想法，你觉得，这道除法题是（）。

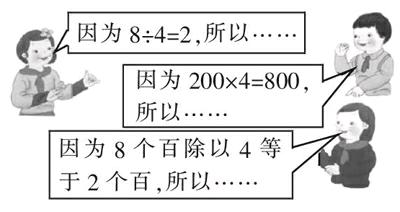
此题呈现了三个小朋友不完整的话语信息，给学生创设了一个“他们究竟在口算哪道题呢”的“破案”场景，显得饶有趣味。每个小朋友的话语信息，恰好对应了“除数是一位数的口算除法”的一种算法，所以通过“破案”活动，学生在不知不觉中有序梳理了口算除法的三种算法。另外，根据一个小朋友的话语信息还不足以揭示真相，如针对第一个小朋友所说的“因为8÷4=2，所以……”，能够联想到80÷4、800÷4、8000÷4等很多算式，但综合三人的所有信息便能锁定“800÷4”这一正解。这个过程，利于学生推理能力的提升。显然，此题之所以是“好题”，是因为它突破了常规题目“根据算式想方法”的定势，彰显了“基于方法寻算式”的新意，真正打开了主动探求、积极思考的情趣性学习空间。

二、“好题”，是有意图的

题目的价值，是促进学生的数学发展。因此，通过每道题的解答，具体促进学生哪个方面的数学发展，这是教师需要时刻关注的。真正的“好题”，并非信手拈来、随意乱用的，而是需要精心设计、适时巧用的。比如，上面的题例1，在其情趣性表象的背后，“帮助学生有效建构口算除法的三种算法”的训练意图是清晰而坚定的。所以，我们必须以“四基”理念为宏观导向，以教材要求为基本线索，细化训练目标，明晰训练落点，设计出指向准、意图明的数学题，来助推学生的数学发展。在当前深化课程改革的背景下，“好题”的意图在以下两个方面尤其要凸显。

其一，夯实意义理解

很多老师都有同感，学生解题的重要意义在于“熟能生巧”。但在笔者看来，这里的“熟”所指向的，不应仅仅是“方法表象”及“答题套路”，更应包括“策略原理”与“意义本质”。只有完满的“熟”，才能生成深度的“巧”。因此，教师在设计题目时，要适时革新“老面孔”、拆除“老包装”、打破“老思路”，在聚焦知识核心不动摇的前提下，加强变式，盘活结构，来唤醒学生对知识内涵的旧理解，促进学生对数学意义的新感悟。

【题例2】“确定位置”原创题（人教版五年级上册）

如图，在直角三角形ABC中，顶点A的位置用数对表示是（10，16），顶点B的位置用数对表示是（8，12），那么，顶点C的位置用数对表示是（  ）。

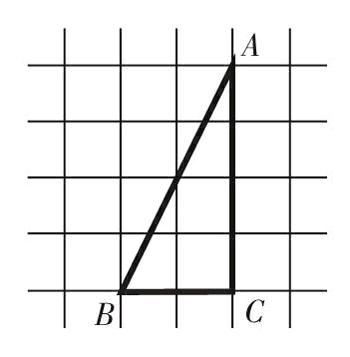
很多关于数对的题，都是给出完整的坐标信息，让学生写出指定位置的“数对”。几次练习后，学生对“数对中前面的数表示列、后面的数表示行”便很清楚了。然而，要帮助学生深度建构“数对”的意义，光凭此类仅靠模仿就能解决的基础题是不够的。此类题目所含的思维空间较窄、探究张力较小，所以，知识意义在学生脑海中的植入度便较低。相比而言，本题有些“不按常理出牌”，隐掉了完整的坐标信息，让学生根据A、B的位置来推断C的位置。在“走迷宫”式的任务情境中，为确定C的位置，学生必然需要自觉解读表示A、B位置的“数对”。而这个解读的过程，就是对“数对”意义的再理解过程。随后，学生会发现C与A同列、与B同行，所以列数与A相同，行数与B相同，由此得出C的位置是（10，12）。这个过程，凸显了对“数对”构成的意义理解，有力拓展了认知深度。

【题例3】“小数乘法”原创题（人教版五年级上册）

学习小数乘法时，我们知道了：“因数中一共有几位小数，就从积的右边起数出几位，点上小数点。”那么，为什么因数中有几位小数，积就是几位小数呢？请以3.76×0.4=1.504为例，说说你的想法。

这道题选自笔者命制的一份区域性质量调测卷，其检测视点在于，学生是否理解了小数乘法的算理，并能用自己的方式清晰表达。如果说，题例2指向的是对知识本身（数对）的意义理解，那么，本题所指向的则是对知识来历（算理）的意义理解。像这样的题目，在“偏重知识运用、忽视原理建构”的传统教学中是极其少见的。从答题情况看，学生之间的差异很大。有些学生能像教材例题那样，以图示、文字等方式呈现“两个因数先看作整数相乘再将积缩小”的动态过程，比较清晰地揭示“积的小数位数”的形成真相;有些学生则备感茫然，写出的答案是“这是一种规定”“老师就是这样告诉我们的”“算起来比较方便”……不同形态的回答所折射出的，是学生对算理理解的真实水平，以及教师教学行为的客观样貌。当前，应该适当加强此类“聚焦原理解读”题目的比重，来引领学生的学与教师的教。

其二，锤炼核心能力

《义务教育数学课程标准》（2011年版）提出了数学课程十大核心词：数感，符号意识，空间观念，几何直观，数据分析观念，运算能力，推理能力，模型思想，应用意识，创新意识。对此，我们也可以理解成，数学课程亟须培养学生这十种核心能力。对于这些核心能力的教学，教师不能停留在观念上、口头上，应落实到行动上（包括题目设计）。也就是说，教师在设计数学题时，应结合具体的教学内容，有意识地将这十种核心能力的检测及锤炼融入其中。由此，既巩固了基础知识，落实了基本技能，又使核心能力的养成落到实处。

【题例4】“图形的旋转”原创题（人教版五年级下册）

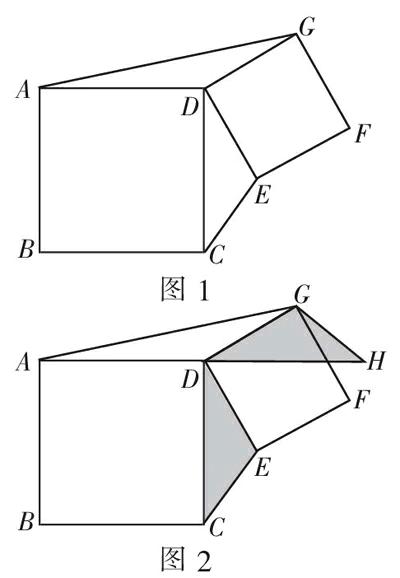
如图1，四边形ABCD和四边形DEFG都是正方形。三角形ADG的面积是10平方厘米，则三角形DCE的面积是（  ）平方厘米。

乍看此题，似乎信息不全，无从下手。事实上，此题为“空间观念”“应用意识”预留了宽绰的“用武之地”。如果学生能够想到将三角形DCE绕D点逆时针旋转90°，问题便可迎刃而解。如图2，围绕D点，线段DC旋转到了DH的位置，线段DE旋转到了DG的位置（DE与DG原本就是正方形的两条边），三角形DCE整体旋转到了三角形DHG的位置。而三角形DHG与三角形ADG等底等高，所以三角形DCE与三角形ADG面积相等，即10平方厘米。这道题中，“将一个三角形逆时针旋转90°”是基本知识点。在一个比较复杂的面积计算情境中，能否想到“通过旋转，寻求关联”，是对学生“空间观念”“应用意识”的有力挑战。经历解答过程后，学生不仅能对“旋转究竟有什么用”产生切身体会，其空间想象能力也会得到有益提升。

当然，指向核心能力锤炼的数学题并非“高大上”。很多时候，我们只需要在常规题目的基础上“跟进一步”即可。

【题例5】“长方形、正方形的面积计算”原创题（人教版三年级下册）

1.算一算：下面图形的面积各是多少？

图3：长4分米、宽3分米的长方形

图4：长28米、宽15米的长方形

图5：边长6厘米的正方形

2.想一想：生活中，这三个图形的大小分别接近于哪个物体的表面呢？请连线。

图3    图4   图5

魔方的一个面  电脑屏幕篮球场

此题中，“算一算”部分属于常规性的面积公式运用，在后面添上“想一想”部分，整道题的立意便被拉高了：引导学生立足基本操练、拓宽认知视野，寻找每个面积的生活原型。在这个过程中，量感得以巩固，应用意识也由此切实强化。

三、“好题”，是有效度的

在力求创新、追寻“好题”的过程中，我们需要始终关注一道“好题”的底线属性：效度。根据“百度百科”的定义，效度是“测量工具所能测出其所要测量特质的程度”。也就是说，题目作为“工具”，用其测量后，所能呈现出的原先想要反映的训练目标或检测目标的程度，即为效度。由于命制过程的种种缺失，当下题目效度缺失的现象并不鲜见。日常教学中，一些题目之所以会引起争论，“效度缺失”便是重要原因。为了确保效度，我们在设计题目时务必遵守两条准则。

其一，要紧扣课程要求

前文谈到，“好题”是有意图的。这个意图，必定依托“课标精神”“教材要求”而确立。在此基础上，从“题目材料的选择”，到“题面信息的形成”，再到“题解思路的预设”都要与测量意图高度匹配。切忌出现有悖于课标要求的内容细节，以免影响题目效度。

【题例6】“左右”测试题（人教版一年级上册）

此题选自某校一年级上学期的一份单元测试卷。有的学生以自己（观察者）为参照点，填了“4”;有的学生则以小红（活动者）为参照点，填了“2”。阅卷时，老师们也展开了广泛讨论。笔者认为，命题者没能把握课标关于第一学段“左右”教学的具体要求：强调以“学生身体”（即“左右手”）为中心辨识左右。而且，《教师教学用书》强调：教师应慎重对待位置关系的相对性问题，不能任意提高教学内容的难度。审视本题，我们不难发现，“小朋友排队”的材料适合于考查“前后”，不适合于考查“左右”。如果非要用这则材料来考查“左右”，必须让小红转过身去，与其他学生身体朝向一致，避免“相对性”带来的难度。由此，题目才能更为真实地检测出每名学生“以自我身体为中心辨识左右”的能力水平。

其二，要避免思维歧义

当前，很多教师都注意了将数学题目与生活场景结合起来，从中体现现实性与应用味，这当然是非常正确的。不过，在充分把握生活资源对数学理解的重要意义的同时，我们也要注意生活经验可能会对解题思路造成的客观干扰，要更为严密地编制题目，确保测量结果的效度。

【题例7】“小数的大小比较”作业题（人教版四年级下册）

下表是五位同学的跳远比赛成绩。

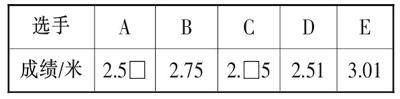
如果C至少是第二名，那么，他跳了（  ）米。

此题顺应了学生熟悉的“跳远比赛”情境，将“小数的大小比较”融合其中，且任务设置富有探究性，将“推理能力”的训练落到实处，确实是一道“好题”。不过，有位学生的解答引起了笔者的思考。别人的答案都是“2.85”（这应该是命题者预设的正确答案），可该生却坚持“2.75”。他的理由是：“题中写着‘至少，那就是说数据要尽量小一些。而C和B‘并列第二名时C的数据是最小的。所以，我认为是2.75米。”你能说这个学生的意见没道理吗？生活中，确实存在“并列名次”这回事儿。生活经验告诉他，要实现“至少”，就很有可能是“并列第二名”。这样一来，“2.85”“2.75”两个答案皆有其合理性了。其实，如果命题者将C的成绩调整为“2.□3”（百分位不是“5”皆可），可能答案就唯一了。