两类四阶非线性微分方程的解法

贾艳萍，李录苹

（山西大同大学数学与计算机科学学院，山西大同037009）

两类四阶非线性微分方程的解法

贾艳萍，李录苹

（山西大同大学数学与计算机科学学院，山西大同037009）

应用变量变换方法,求解两类可化为一阶可积类型的四阶非线性微分方程,扩大了变量变换方法的使用范围。

变量变换;微分方程;通解

常微分方程的解法[1-5]众多，变量变换是求解常微分方程的常用技巧。它将方程的原变量用新的变量替换，使得原方程变为相对易求解的类型。本文将通过变量变换求解两类四阶非线性微分方程。

定理1四阶微分方程

通过变量替换可求出通解，其中a1，a2为常量，p，f是连续函数。

证明原方程可变形为

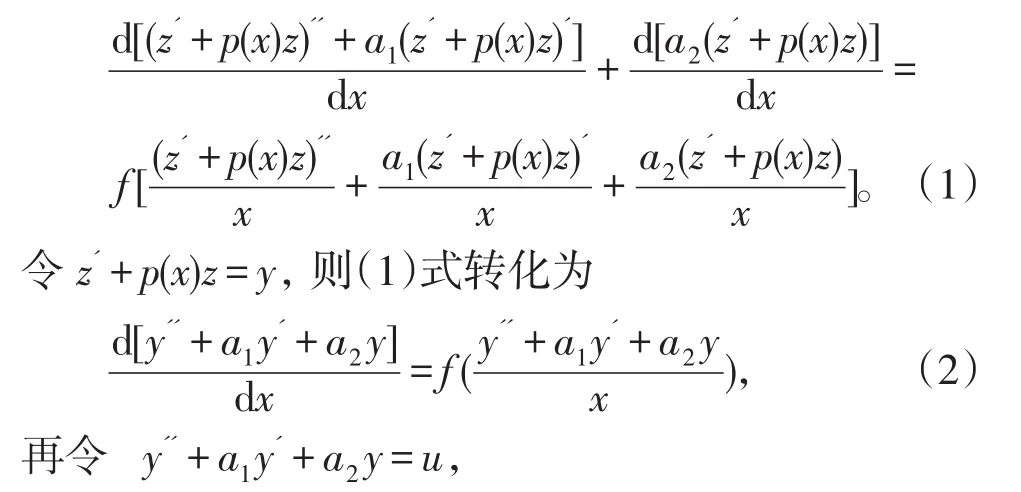
则（2）式转化为

此为齐次方程[5]，作变换u=vx，则（3）可转化为变量分离方程[5]

可得（4）的通解为v=v(x,c1)，

于是（3）的通解为u=xv(x,c1)。

由二阶非齐次线性方程[5]的解法求出

y''+a1y'+a2y=xv(x,c1)的通解y=y(x,c1,c2,c3)。

再由常数变易法[5]求出

z'+p(x)z=y(x,c1,c2,c3)的通解z=z(x,c1,c2,c3,c4)，

其中c1,c2,c3,c4为任意常数。

解：原方程可以改写为

上式可写为

由定理1，令z'+z=y，则（5）式转化为

于是（6）式变为

解得（7）的通解为u=c1x，

再由比较系数法可求出

y''+2y'+y=c1x的一个特解为=c1x-2c1，

则y''+2y'+y=c1x的通解为

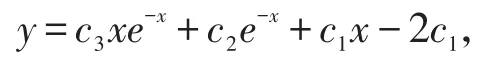
又因为z'+z=0的通解为z=c4e-x，

从而由常数变易法可得

z'+z=c3xe-x+c2e-x+c1x-2c1的通解为

其中c1,c2,c3,c4为任意常数。

定理2四阶微分方程

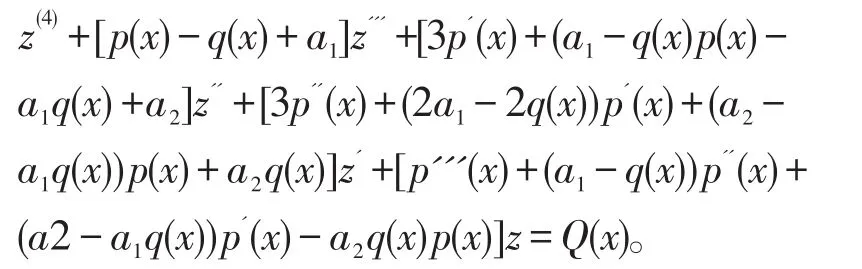
通过变量替换可求出通解。其中a1，a2为常数，p(x)，q(x)，Q(x)是连续函数。

证明原方程可改写为

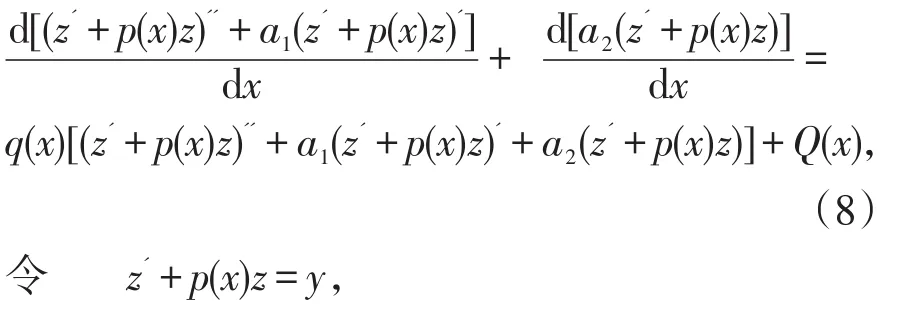
则（8）式转化为

则（9）式转化为

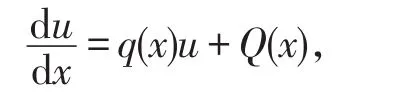
由常数变易法可求出其通解u=u(x,c1)，在由二阶非齐次线性方程的解法可求出y''+a1y'+a2y=u(x,c1)的通解为y=y(x,c1,c2,c3)，再由常数变易法求出z'+p(x)z=y(x,c1,c2,c3)的通解为z=z(x,c1,c2,c3,c4)，其中c1,c2,c3,c4为任意常数。

例2求方程

（10）式可化为

于是（11）式可转化为

由常数变易法可解得（12）的通解为，

再通过高阶方程的降阶可求得

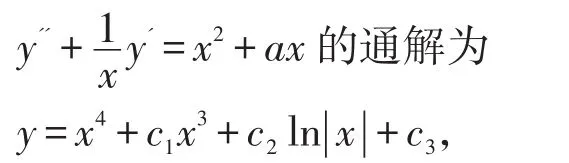
最后由常数变易法求出

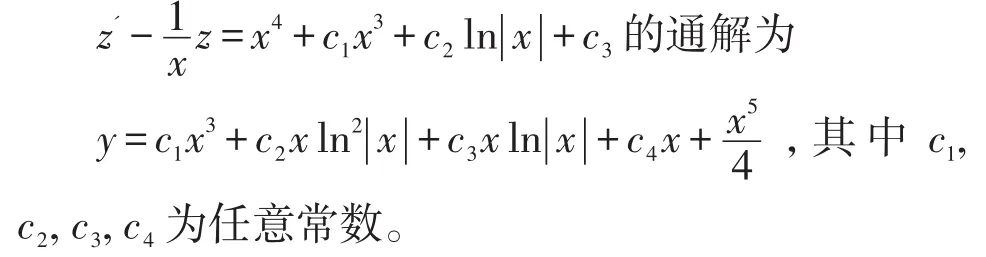
[1]肖菊霞.几类一阶常微分方程及其解法[J].考试周刊,2014(64)：50-51.

[2]董晓红.常微分方程不同解法比较[J].包头职业技术学院学报,2012,13(1)：89-91.

[3]姜嵛芃.二阶变系数常微分方程解法研究[J].金融理论与教学,2012(4)：90-91.

[4]王柔怀,伍卓群.常微分方程讲义[M].北京：人民教育出版,1963.

[5]王高雄,周之铭.常微分方程[M].北京：高等教育出版社,2001.

The Solution of Two Classes of Fourth Order Nonlinear Differential Equation

JIA Yan-ping,LI Lu-ping
(School of Mathematics and Computer Sciences,Shanxi Datong University,Datong Shanxi,037009)

This paper applies variable transformation method to solve the two classes of fourth order nonlinear differential equation.

variable transformation,differential equation;general solution

O175.1

A

1674-0874(2015)04-0012-02

2015-04-20

贾艳萍（1982-），女，山西朔州人，硕士，讲师，研究方向：泛函分析。

〔责任编辑 高海〕