基于ADINA的预制装配式钢筋混凝土楼板整体性计算分析

张玉敏，张国秀，苏幼坡

(华北理工大学 河北省地震工程研究中心，河北 唐山 063009)



基于ADINA的预制装配式钢筋混凝土楼板整体性计算分析

张玉敏，张国秀，苏幼坡

(华北理工大学 河北省地震工程研究中心，河北 唐山 063009)

有限元方法；预制楼板;整体性；叠合楼板；应变

采用有限元软件ADINA建立了4种方案的钢筋混凝土楼板在平面内荷载作用下数值模型，分析楼板的变形性能及实际所具有的自身平面内的刚度。计算结果表明，预制楼板在平面内的刚度随预制楼板接缝连接刚度的降低而降低。当能保证预制装配式楼板接缝质量时，其性能接近现浇楼板。叠合楼板现浇层在预制装配式楼板接缝存在软弱夹层时才起作用。新型预制楼板的性能接近普通预制楼板。

0引言

由于装配式钢筋混凝土结构构件之间连接可靠性差，以及对其抗震性能研究较少，因此在抗震设防地区的使用受到限制，有关预制混凝土结构应用的规定也偏于保守。但在近来的一些震害调查和试验研究工作表明，预制装配式混凝土结构体系也有较好的抗震性能[1-3]。美国统一建筑规范(UBC97)中规定可以在高烈度地震区使用预制装配式钢筋混凝土结构，其前提是通过试验和分析证明，该结构在强度、刚度方面具有甚至超过相应的现浇混凝土结构[4-5]。

建筑抗震设计规范中规定在计算地震内力时采用楼板平面内刚度为无限大的假定，即不考虑楼板在自身平面内的变形。这一假定减少了结构位移的自由度数目, 简化了计算工作。一般情况下, 高层建筑结构内力与位移分析采用这一假定可以满足要求。但是, 在有些情况下则有必要考虑楼板变形产生的影响, 尤其是楼板刚度较小、主要抗侧力结构间距大以及层数较少时, 楼板平面内变形影响较显著, 这时就不能将楼板平面内刚度视为无限大。据参考文献[6]国外一些资料认为, 楼板在平面内荷载(楼层地震力)的作用下，只有相对水平挠度小于 1/50 000时, 才能认为平面内刚度无限大。我国在过去实行的建筑抗震设计规范中规定，相对水平挠度 L/12 000为楼盖水平刚度可被假定为无限大的界限。若不满足此规定，则需要对计算的结构地震内力及位移进行调整。这是根据我国沿用的设计计算方法及有关研究成果经综合分析后得出的结论[7]。楼板的相对水平挠度是将楼板作为支承在抗震墙上的弹性简支深梁, 并近似按铁木辛柯的弹性力学公式计算的[8]。现行抗震设计规范GB50011-2010[9]中,对建筑体型的长宽比、柱距及抗震墙之间的距离做出限制，就是基于以上的结论做出的,其目的是为了保证楼板平面内刚度为无限大假定的合理性。

1新型预制楼板的提出

施工采用现浇楼板方案时，不存在水平接缝，楼板的整体性能好，认为平面内刚度是无限大不存在问题，但整个楼板均为现浇需现场立模，不仅工作量大，而且模板周转慢，施工对周边环境影响大[10-11]。对预制装配式钢筋混凝土楼板,虽然克服了以上的问题，但在安装后需要在两块预制板之间设置一定宽度的后浇带(板缝混凝土)，由于施工质量等因素的影响，当新、老混凝土之间结合性能不好，存在软弱夹层时，在水平地震力的作用下，无论是沿着板缝方向还是垂直于板缝方向作用，软弱夹层两侧的混凝土都将发生相对滑动，使楼板平面内刚度降低。为了满足上述对楼板平面内刚度要求，可在楼板上表面加设配筋的现浇层，形成叠合楼板。这种作法虽然能提高装配式钢筋混凝土楼板的整体性, 使其在地震力作用下的水平挠度减小，但同时也增加了楼板自重, 相应地使地震力增大, 从而反过来可能加大了楼板的水平挠度，且湿作业仍然较大而且受楼板整体厚度制约，往往现场浇筑时仍需对预制楼板加支撑，未能真正体现工业化效果，综合各方面因素来看其有利性也是有待商榷的[12]。

针对预制装配式剪力墙结构体系，为了保证预制墙体接缝部位的整体性，结合楼板的受力特点，华北理工大学张玉敏教授提出了一种“墙板节点部位楼板现浇，中间部位楼板采用预制装配”的新型预制楼板方案，如图1所示。现浇部位底部不必设置落地支撑脚手架，上层楼板的自重及施工荷载不传递到下层楼板。现浇部分楼板占整个楼板的 20%以下，减少了现场模板的数量，提高了施工效率。预制楼板与现浇楼板的连接部位可按简支楼板受力特点设置接缝做法，不必预留过长的受力钢筋，安装工作方便、安全。

图1　新型预制装配式楼板安装　　　　　　　　　　　　　　　　图2　新型预制楼板平面图

由于结构上的复杂性，除现浇楼板外，以上几种形式的楼板在平面内受力时的挠度不能用铁摩辛柯梁公式计算，可以采用有限元数值分析方法计算。在本文中，对一栋预制装配式钢筋混凝土剪力墙结构中的某一个楼板单元进行数值模拟分析计算，考察各种方案条件下楼板平面内的刚度和变形特点,分析不同因素对楼板整体性的影响。

2楼板有限元模型

若取整个楼层的楼板建立有限元模型，则由于规模较大，计算不便。因此只取开间为 3.6 m，进深 4.2 m的一块楼板做为计算单元。包括 5块预制板及 4条板缝混凝土后浇带。预制楼板与现浇楼板的构造分别参照相关设计规范及构造图集。由于计算单元的平面尺寸小，计算单元的刚度比整层楼板或抗震墙之间的楼板平面内的刚度大，为了使楼板在平面内荷载作用下发生明显的位移和变形，在其平面内以体积力的形式施加 10倍楼板自身重量的荷载，分析分别采用现浇楼板方案、预制楼板方案、叠合楼板方案和新型预制楼板方案时，楼板平面内的变形及之间的差异特点。

采用ADINA软件建立有限元数值分析模型。混凝土采用软件内置的 Concrete材料模型，钢筋采用Bilinear弹塑材料模型。混凝土采用三维Solid单元，钢筋采用Rebar单元。在混凝土Solid单元划分时自动生成Rebar单元，与Solid单元共用节点，并考虑了与周围混凝土的粘结作用。混凝土与钢筋力学性能参数如表1～2所示。

表1　楼板C30混凝土单向应力状态下力学性能参数(标准值)

表2　楼板钢筋力学性能参数(标准值)

为了模拟预制楼板混凝土与现浇混凝土在交界面上的粘结滑移作用，在这两部分混凝土之间嵌入一层虚拟的弹性薄膜，厚度为 20 mm，以其弹性常数E的大小反应两侧混凝土之间相互作用的强弱。弹性薄层与两侧混凝土在接触面上用Face-link方式连接，与两侧混凝土单元共用节点，类似于岩石力学有限元分析中采用的Goodman单元[13]。

3计算结果及分析

根据计算结果考察楼板平面内任一点位移的大小及平面内应变值的大小反应楼板平面内的位移及变形。为了表示方便，按如下的规则表示云图数据。

(1)沿预制板长方向或短边方向为纵向；垂直于预制板长方向或沿长边方向为横向。

(2)在纵向位移云图中，白色区域代表位移 |d|>0.05 mm，在横向位移云图中，白色区域代表位移|d|>0.05 mm；在纵向与横向应变云图中，白色区域代表应变值 |ε|>10-6。

计算结果如图3～图6所示。

2.1现浇楼板计算结果

(a)纵向位移(白色区域位移 |d|>0.05 mm)(b)纵向应变(白色区域应变值 |ε|>10-6)

(c)横向位移(白色区域位移 |d|>0.03 mm)(d)横向应变(白色区域应变值 |ε|>10-6)

2.2普通预制楼板计算结果

(a)纵向位移(白色区域位移 |d|>0.05 mm)　　　　　(b)纵向应变(白色区域应变值 |ε|>10-6)

(c)横向位移(白色区域位移 |d|>0.03 mm)　　　　(d) 横向应变(白色区域应变值 |ε|>10-6)

2.3叠合楼板计算结果

(a)纵向位移(白色区域位移 |d|>0.05 mm)　　　　(b)纵向应变(白色区域应变值 |ε|>10-6)

(c)横向位移(白色区域位移 |d|>0.03 mm)　　　　　(d)　横向应变(白色区域应变值 |ε|>10-6)

(a)纵向位移(白色区域位移 |d|>0.05 mm)　　　　(b)纵向应变(白色区域应变值 |ε|>10-6)

(c)　横向位移(白色区域位移 |d|>0.03 mm)　　　　(d)横向应变(白色区域应变值 |ε|>10-6)

2.4新型预制楼板计算结果

(a)　纵向位移(白色区域位移 |d|>0.05 mm)　　　　　(b)纵向应变(白色区域应变值 |ε|>10-6)

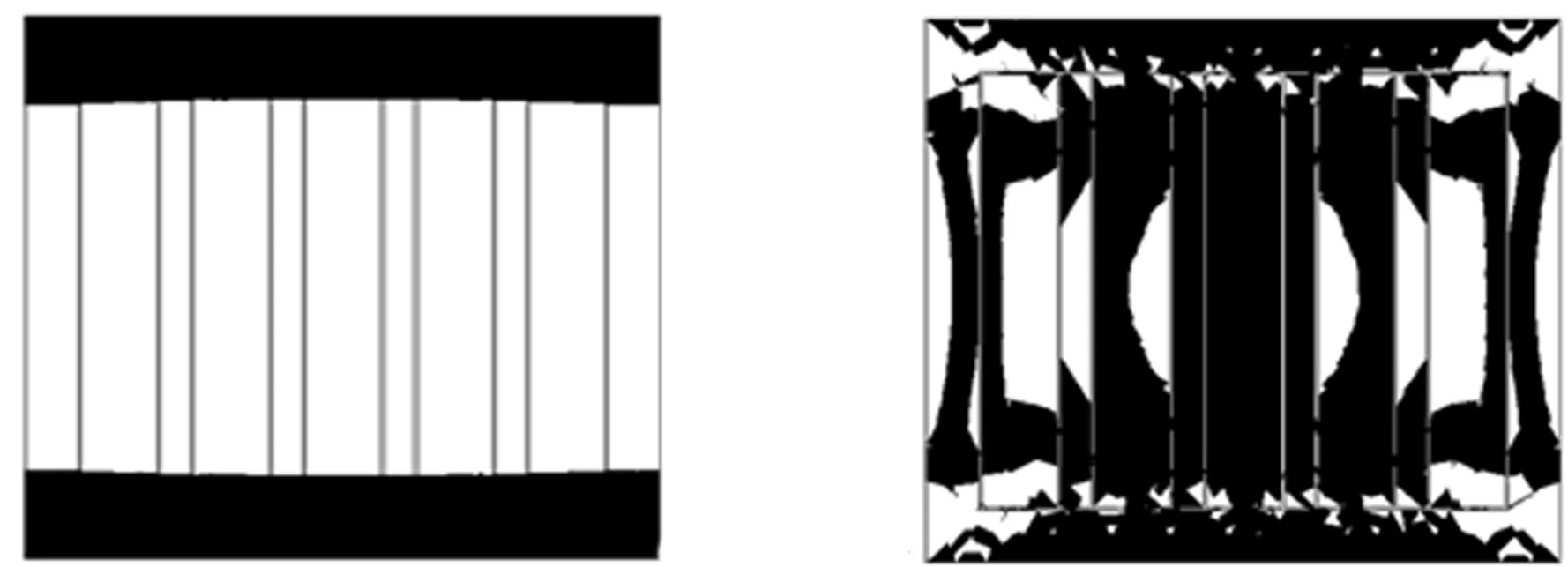
(c)　横向位移(白色区域位移 |d|>0.03 mm)　　　(d)　横向应变(白色区域应变值 |ε|>10-6)

预制板及叠合楼板薄弱连接夹层的刚度与楼板相对位移之间的关系如图7～图8所示。

图7　楼板平面内最大位移与薄层弹性常数(混凝土初始弹性模量 Ec=30 000 MPa)

图8　楼板平面内最大位移与薄层弹性常数(混凝土初始弹性模量 Ec=20 000 MPa)

从图3～图6可以看出，当弹性薄层的弹性常数为混凝土初始弹性模量的 1/10左右，即E1=2 000 MPa时，在有预制板的方案中，楼板平面内位移及应变较大的区域明显增加，在软弱夹层附近应变值均较大。而从图 7～8楼板平面内最大位移与弹性薄层弹性模量之间的关系可以看出，当E1=100～1 000 MPa时，楼板平面内最大位移增加很快，使楼板平面内刚度急剧降低。由于对楼板平面内最大位移的限值规定较严(我国规范规定 1/12 000)，因此这时往往不能满足对楼板平面内刚度无限大的假定。只有当E1>10 000 MPa时，预制楼板体系的平面内最大位移才与现浇楼板的值相接近。当普通预制楼板存在软弱夹层时，叠合楼板能部分抵消其影响，增加平面内的刚度。若不存在软弱夹层，则叠合层混凝土不起作用。这时没有必要设置，造成材料用量增加。新型预制装配式楼板与普通预制装配式楼板的位移与应变特性接近。

4结论

(1)当楼板接缝处的粘结强度及刚度降低时，无论沿横向还是沿纵向，楼板在平面内的刚度都表现为急剧降低；而当不存在软弱夹层时，预制装配式楼板与现浇楼板的特性相近。

(2)只有当预制装配式楼板体系存在软弱夹层时，叠合楼板才能发挥增加楼板平面内刚度的作用，若能保证预制装配式楼体系接缝的质量，则可不设叠合层现浇楼板。新型预制装配式楼板的位移及应变特性与普通预制装配式楼板接近。

[1]薛伟辰.预制混凝土框架结构体系研究与应用进展[J]. 工业建筑,2002, 32(11):47-50.

[2]柳炳康,施法科,刘海涛,等.反复荷载作用下预压装配式框架结合部受力性能[J]. 合肥工业大学学报(自然科学版),2005, 28(01):71-74.

[3]徐有邻.由地震引发对预制预应力圆孔板的思考[J]. 建筑结构,2009,38(07):7-9.

[4]Frosch R J.Shear transfer between concrete elements by using steel pipe connection[J].ACI Structural Journal,1999,96(06):1003-1008.

[5]David Arditi, Uluc Ergin, Suat Gunhan.Factors affecting the use of precast concrete systems[J]. Journal of architectural engineering.2000, 06(03):79-86.

[6]侯霍岩.装配式钢筋混凝土楼盖在水平荷载往复作用下的变形性能[J]. 重庆建筑工程学院学报,1985,(02):36-51.

[7]赵西安.楼板变形对高层建筑结构内力与位移的影响及其计算[J]. 建筑结构,1982,(06):1-9.

[8]S P Timoshenko, J N Goodier.Theory of Elasticity[M]. 北京:清华大学出版社,2004.

[9]建筑抗震设计规范GB50011-2010[S]. 北京:中国建筑工业出版社, 2010.

[10]卢锡鸿.对我国预制构件行业起落的反思及发展意见[J]. 建筑技术,2000, 32(02):82-87.

[11]吴晓泉.闻德荣.我国混凝土行业空前发展的一年: 2003年技术经济指标简要分析[J]. 混凝土,2004,(07):7-11.

[12]桑爱华, 林远征.预应力薄板叠合楼板的研究和应用[J]. 建筑技术,1984,(11):1-9.

[13]江见鲸, 陆新征, 叶列平.混凝土结构有限元分析[M]. 北京:清华大学出版社,2005.

Computational Analysis about Integrity for Prefabricated RC Floor Slab Based on ADINA Software

ZHANG Yu-min,ZHANG Guo-xiu,SU You-po

(Earthquake Engineering Research Center of Hebei Province,North China University of Science and Technology,Tangshan Hebei 063009,China)

finite element method;pre-cast floor slab;integrity;laminated floor slab;strain

With finite element software ADINA, numerical models about 4 schemes of floor slab were presented for analyzing deformation performance subjected to in-plane load. Results show that in-plane stiffness of pre-cast floor slab will decrease with stiffness reduction of linking layer between the pre-cast concrete and the cast-in-situ concrete. The deformation performance of pre-cast for slab could be close to cast-in-situ floor slab, provided quality of concrete of linking layer could be ensured. The cast-in-situ layer of laminated floor slab will present its contribution on only if there exists faulty linking layer in pre-cast layer. In the same way, the deformation performance of new type of pre-cast floor slab is similar to traditional pre-cast floor slab.

2095-2716(2015)04-0083-08

TU375.2

A