基于Map/Reduce的外壳片段立方体并行计算方法

唐珊珊，朱跃龙，朱凯

河海大学计算机与信息学院，南京210098

◎数据库、数据挖掘、机器学习◎

基于Map/Reduce的外壳片段立方体并行计算方法

唐珊珊，朱跃龙，朱凯

河海大学计算机与信息学院，南京210098

针对高维、维度分层的大数据集，提出一种基于Map/Reduce框架的并行外壳片段立方体构建算法。算法采用Map/Reduce框架，实现外壳片段立方体的并行构建与查询。构建算法在Map过程中，计算出各个数据分块所有可能的数据单元或层次维编码前缀；在Reduce过程中，聚合计算得到最终的外壳片段和度量索引表。实验证明，并行外壳片段立方体算法一方面结合了Map/Reduce框架的并行性和高扩展性，另一方面结合了外壳片段立方体的压缩策略和倒排索引机制，能够有效避免高维数据物化时数据量的爆炸式增长，提供快速构建和查询操作。

联机分析处理；外壳片段立方体；Map/Reduce技术；并行计算

1　引言

数据立方体（Data Cube）［1］物化能够提高OLAP的性能，但完全物化通常需要很高的时空成本。为提高数据立方体生成和查询效率，许多专家学者提出Iceberg Cube［2］、Condensed Cube［3］和Quotient Cube［4］等数据立方体物化方法，这些方法在多维分析应用中起着重要的作用。物化高维数据集时，数据立方体体积将随着维度个数的增加呈指数级增长，导致十分昂贵的物化代价。采用上述物化方法，只能延迟这种数据量爆炸，不能从根本上解决问题。文献［5］提出外壳片段立方体的概念，有效避免高维数据立方体体积爆炸式增长。然而，在数据量非常庞大的情况下，计算外壳片段立方体时间成本仍然很高，并行计算是行之有效的解决办法。Google公司提出的Map/Reduce［6］是一种实现分布式计算任务的并行框架，它将海量数据处理任务划分为Map过程和Reduce过程，用户只需考虑如何自定义Map函数和Reduce函数以满足业务需求，而不需要考虑复杂的底层分布式计算实现细节。

水利普查成果数据具有覆盖面广、数据量大、维度多、维度分层等特点，数据维度可以达到20个，记录数也常常超过106条，物化水利普查成果数据立方体需要很高的时空成本［7］。本文提出一种基于Map/Reduce框架的外壳片段立方体并行计算方法，提高水利普查成果数据立方体构造与查询的效率。

2　数据立方体

在数据仓库中，数据立方体可以用Cube=（D，M）来表示。D=｛D1，D2，…，Dm｝是维度集合，其中m≥1，Di=（DHi，σ）表示一个维度属性，DHi表示Di所有层次组成的一个有序集合，即，h代表Di的维层次数，是维度Di的第j层，σ是DHi维层次上的偏序依赖关系；M=｛M1，M2，…，Mn｝是度量集合，其中n≥1，Mi表示一个度量属性。

为了便于本文论述，以水利普查成果数据中水库工程对象数据事实表为例，此事实表包括：行政区划（addvcd）、工程规模（gcgm）、水库类型（sklx）和建设情况（jsqk）四个维度和总库容（zkr）一个度量，如表1所示。

表1　水库工程事实表

其中行政区划维addvcd分为省（province）、市（city）、县（county）三个层次，即DHaddvcd=（province，city，county）。其中，province的最大成员个数为32，city的最大成员个数为21，county的最大成员个数为31。

2.1外壳片段立方体

定义1（外壳片段立方体Shell Fragments Cube）对于一个n维的高维数据立方体Cube（D，M），将维度集合D=｛D1，D2，…，Dn｝按照互不相交的原则，分割为k个独立片段，物化这k个独立的片段并创建倒排索引。对于M=｛M1，M2，…，Mn｝度量集合，创建度量索引号对照表（TID_measure表）。

2.2层次维编码

水利普查成果数据中存在3个核心的层次维（行政区划、水资源区划和流域水系），对水利普查成果数据分析有着举足轻重的作用，为保持层次维上的偏序依赖关系，提高OLAP查询效率，引入压缩性能强且具有层次语义特性的层次维编码，代替原表中关键字［8-10］。

定义2（层次维编码）［8-10］层次维Di的层次维编码，是维度Di中所有层次属性采用混合索引（B-tree和bit code）技术进行二进制编码，按层次由高到低，依次组合而成的混合编码。每层编码位数为，其中mj为层最大成员个数。

例1：层次维addvcd中层次province编码位数为，层次city编码位数为，层次county编码位数为，那么Baddvcd位数为5+5+5=15， addvcd层次维编码如表2所示。

表2　addvcd层次维编码

定义3（位掩码）［9］维层次的位掩码表示维度Di的层及其祖先层次位编码值为1，其子孙层次位编码值为0的混合编码。

定义4（编码前缀）维度Di维成员的层编码前缀，由位掩码与层次维编码按位与操作计算得到，即。

利用层次维编码具有前缀层次语义特性，求得各维相应维层次属性的编码前缀及其TID关联关系。表2中维度addvcd中层次city的编码前缀及其TID关联关系如表3所示。

表3　维层次city的编码前缀及其TID关联表

2.3外壳片段分段方法

外壳片段立方体需将维度集合D=｛D1，D2，…，Dn｝划分为k个互不相交的维片段，依次对维片段编号FID，并保存FID与维度对照表FID_dimensions。对于具有层次维的数据集，片段划分存在两种情况：

（1）非层次维，根据查询需求，将频繁查询的维度或者需一起查询的维度定制到同一个维片段中，维片段大小为f（其中2≤f≤4）［10］，聚集cuboids形式如：｛［Di，Di+1，Di+2］，…，［Dn-2，Dn-1，Dn］｝，对于每个维片段，计算其数据立方体并创建倒排索引。

（2）层次维，计算层次维编码，根据位掩码计算出该维度各层次的编码前缀，聚集cuboids的形式：｛［PrefixB1（Di），PrefixB2（Di），…，PrefixBh（Di）］，…，［PrefixB1（Dj），PrefixB2（Dj），…，PrefixBh（Dj）］｝，对每个片段创建倒排索引。一个层次维的聚集cuboids已经较为复杂，因此设为一个单独的维片段。

3　外壳片段立方体并行计算与查询

Map/Reduce是大数据并行计算的核心技术，给用户提供了简单、易用的功能接口以及与性能相关的调优参数。其中，Map过程将原始的海量数据划分为不同的数据子集，并根据用户自定义的Map函数对每一个数据子集进行映射处理；Reduce过程将Map过程处理后的结果根据用户自定义的Reduce函数进行归约处理［11-13］。本文提出基于Map/Reduce框架的外壳片段立方体并行计算方法（Parallel computation of Shell Fragments Cube，PSFC），算法主要分为Map和Reduce两个过程［14-15］，使用水利普查机电井对象脱密数据，维片段划分：层次维作为单独的维片段，非层次维划分为大小为3的维片段，具体描述如下：

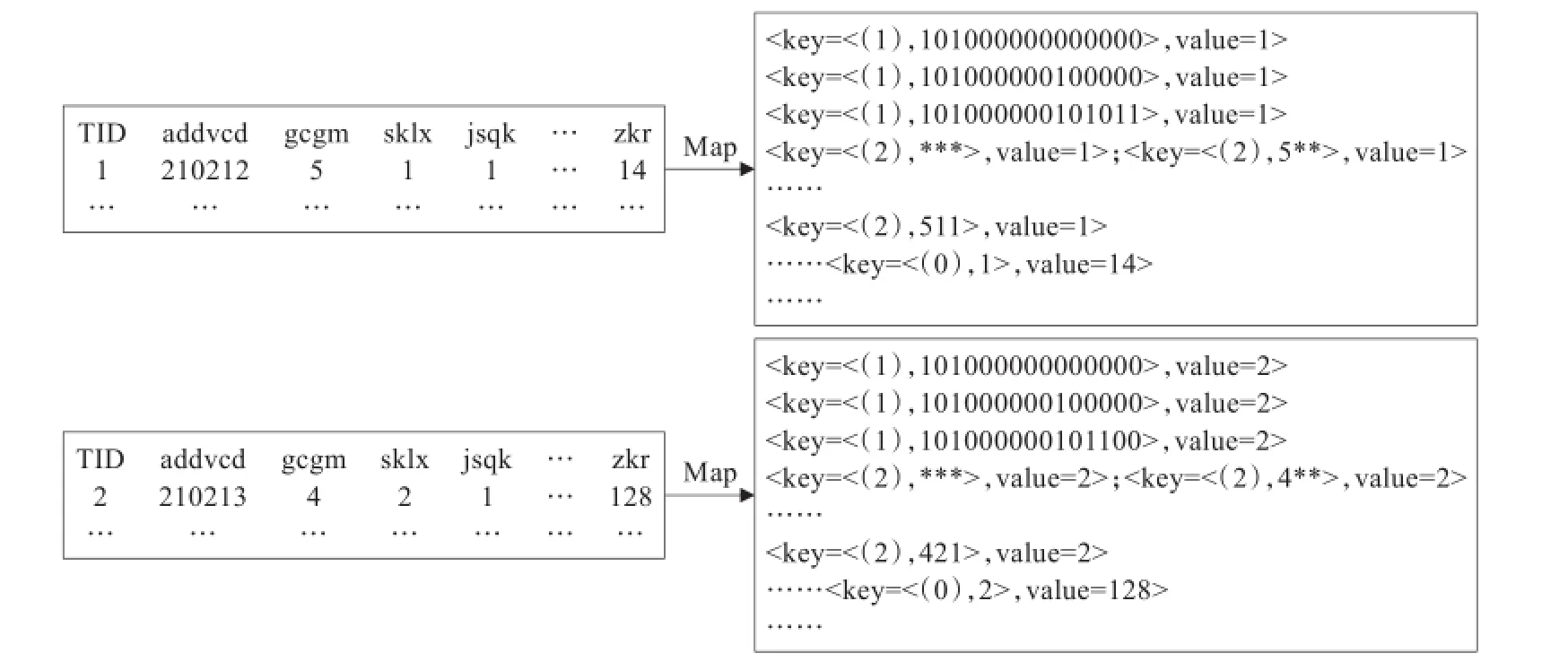
图1　Map过程实例图

3.1并行计算方法

（1）Map过程

Map过程首先将原始的海量数据划分为不同的数据子集，然后自定义Map函数根据片段编号维度对照表（FID_dimensions表），对数据进行逐条处理，输出映射处理后的key/value键值对［16］。对每条数据处理分为以下三种情况：

①对于层次维，根据编码前缀定义计算出该维各层次的编码前缀｛PrefixB1，PrefixB2，…，PrefixBh｝，并映射成形式为＜key=＜FID，PrefixBi＞，value=TID＞的键值对，其中FID代表片段编号，TID代表行索引号。

②对于非层次维，根据FID_dimensions表，将属于同一个维片段的维数据片段采用BUC算法，自底向上深度优先生成其所有可能的数据元组，即计算出该数据片段的完全数据立方体。并处理成形式为＜key=＜FID，tuplei＞，value=TID＞的键值对，其中tuplei代表可能的数据单元；

③对于度量，标记其key的第一个属性取值为0，生成形式为＜key=＜0，TID＞，value=measure＞的键值对，其中measure代表度量取值。Map过程示例图如图1所示。

Map函数形式化描述如下：

输入：＜key=TID，value=C＞，其中C代表一条原始数据；

输出：①层次维度：＜key=＜FID，PrefixBi＞，value= TID＞；②非层次维度：＜key=＜FID，tuplei＞，value= TID＞；③度量：＜key=＜0，TID＞，value=measure＞。

shuffle过程包含在Map和Reduce两端中，本文算法在Map端的shuffle过程中，通过重新定义Partition函数［16］的分发规则：将Map过程输出的所有键值对中具有相同片段编号（FID）的key/value键值对，分发到相同的组中，最终将同一组的数据传送到相同的Reduce节点上进行处理。

（2）Reduce过程

Reduce过程接收shuffle过程处理得到的属于同一组的数据集，交给自定义的Reduce函数进行处理，由于同一个Reduce处理的键值对中FID的取值相同，那么每个Reduce的处理结果即为一个外壳片段或TID_measure表。数据处理分为以下三种情况：

①对于层次维，将key值中PrefixBi相同的键值对进行合并，其中value值求并集，处理输出形式为：＜key= PrefixBi，value=＜TID1，TID2，…，TIDj＞＞。该Reduce过程处理结束，即得到一个层次维片段及其倒排索引。

②对于非层次维，将key值中非层次维聚集单元相同的键值对进行合并，其中value值求并集，输出形式为：＜key=tuplei，value=＜TID1，TID2，…，TIDj＞＞。该Reduce过程处理结束，即得到一个非层次维片段及其倒排索引。

③对于度量，即key值中第一个属性为0的键值对，处理输出形式为：＜key=TID，value=measure＞。该Reduce过程处理结束，即得到该外壳片段立方体的TID_measure表。Reduce过程示例图如图2所示。

Reduce函数形式化描述如下：

输入：shuffle过程输出；

输出：所有外壳片段及其倒排索引，以及度量索引表（TID_measure表）。

图2　Reduce过程实例图

3.2并行查询方法

并行查询算法也主要分为两个阶段：Map过程和Reduce过程。若查询条件中包含层次维，将其预计算为层次维编码或编码前缀。

Map过程，遍历外壳片段立方体所有的键值对，查找出符合查询条件的键值对并输出；自定义Map函数中定义一个全局变量flag，（取值为1表明该片段包含所需维度，则遍历该片段；取值为0表明该片段不包含所需维度，则忽略该片段），以此减少Map函数处理键值对数量，提高查询性能。

Reduce过程，对Map过程处理所得的键值对，取其value值进行求交集运算，得到符合查询条件的索引号集合QList。在TID_measure中取出QList对应的度量值，根据给定的聚集函数（本文定义聚集函数为求和sum），计算出用户所需的聚集结果。

输入：①已预计算的外壳片段集合｛fragment1，fragment2，…，fragmentk｝；②TID_measure表；③＜d1，d2，…，dn，M＞形式的查询条件。

输出：查询结果。

4　性能分析

实验一比较传统外壳片段立方体与本文的PSFC方法构造性能，实验二比较集群节点数量对PSFC方法和并行查询算法的影响，并对实验结果进行分析。实验Hadoop集群环境由6台机器组成，包含1个主控节点Master和5个从属节点Slave，它们通过路由器互连。6台节点硬件配置相同（CPU/内存/存储空间：双核2.5 GHz/1 GHz/10 GHz）。搭载的操作系统均为Ubuntu 14.10，Hadoop版本号是0.20.203.0，基于jdk1.7.0_15搭建。实现语言为java，平台eclipse，集群基本信息和网络配置情况如表4所示。

表4　实验所用集群的配置

实验采用水利普查机电井对象脱密数据，有10个维度属性（行政区划、流域水系、水资源区划、流域片、机电井类型、井壁管材料、应用状况、所在地貌类型、水源类型、主要取水用途）和5个度量属性（实际灌溉面积、供水井数量、取水量、实际供水人口、人均取水量），数据量为5×106条，实验前已对各字段都进行规范化处理。

实验一对传统外壳片段立方体方法和PSFC方法构造时间进行比较，图3中shell fragment cube曲线表示传统外壳片段立方体方法，PSFC曲线表示本文PSFC方法，实验运行在节点数为6的集群上，维度数目为10，比较数据量由1×106到5×106条的情况。由图3可以看出，当数据量较少时，PSFC方法的优势不太明显，构造时间大约是传统方法的2/3，这是由于集群需要额外的通讯和数据传送等开销。随着数据量的不断增大，PSFC方法的优势越来越明显，到5×106条数据时，构造时间小于传统方法的1/4。并且随着数据量的上升，传统方法的构造时间上升较快，而PSFC方法的构造时间缓慢升高。这是因为随着数据量的提高，集群开销远小于构造时间，并行优势和算法改进得到体现。

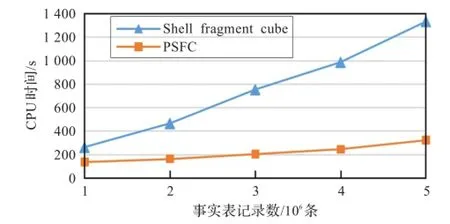
图3　不同数据量构造时间比较

实验二比较集群节点数对并行构造PSFC方法和查询算法的影响，实验数据维度数目为10，数据量为1×106条，集群节点数量由3增加到6。图中Construction代表并行构造曲线，Search曲线代表并行查询曲线。实验结果如图4所示，随着集群节点数量的增加，构造时间接近于线性减少，而查询时间变化较小。原因在于外壳片段的构造相对费时，集群节点的增加会带来较大的收益，而查询的大部分时间被花费在节点之间的通讯和协调代价上。综上，PSFC方法具有良好的可扩展性，根据具体应用环境中数据量的不同，系统可以通过调整集群节点数量，有效地调整并行外壳立方体构造的效率。

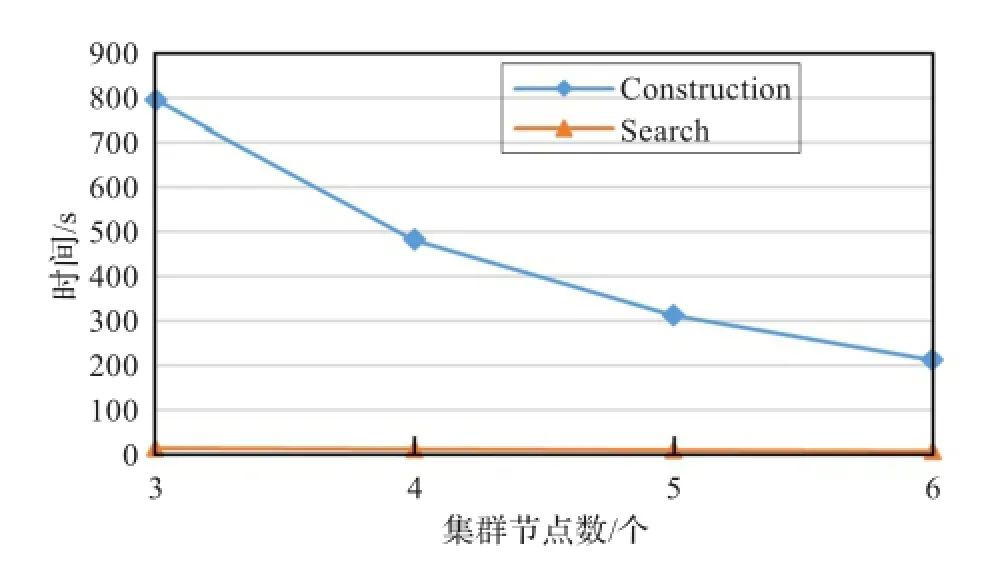
图4　集群节点数量影响

5　结语

文中提出基于Map/Reduce框架的外壳片段立方体并行计算方法和并行查询方法。性能分析表明，相对于串行外壳片段立方体，并行计算方法的性能在高维、数据量大时有显著的优势，可支持水利普查维度多、数据量大的数据立方体计算与查询。当然，本文方法还有很多需要研究和改进的地方，比如在Map/Reduce计算时的调度优化，增量更新维护方面的性能表现，以及如何进一步加快查询响应时间等，都是值得研究的方向。

［1］Gray J，Chaudhuri S，Bosworth A，et al.Data cube：A relational aggregation operator generalizing group-by，cross-tab，and sub-totals［J］.Data Mining and Knowledge Discovery，1997，1（1）：29-53.

［2］Jiang F M，Pei J，Fu A W.Ix-cubes：iceberg cubes for data warehousing and Olap on xml data［C］//Proceedings of the Sixteenth ACM Conference on Conference on Information and Knowledge Management.ACM，2007：905-908.

［3］Wang Z，Xu Y.Minimal condensed cube：data organization，fast computation，and incremental update［C］//International Conference on Internet Computing in Science and Engineering.IEEE，2008：60-67.

［4］Li C，Cong G，Tung A K H，et al.Incremental maintenance of quotient cube for median［C］//Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.ACM，2004：226-235.

［5］Li X，Han J，Gonzalez H.High-dimensional OLAP：A minimal cubing approach［C］//Proceedings of the Thirtieth International Conference on Very Large Data bases-Volume 30，VLDB Endowment，2004：528-539.

［6］Dean J，Ghemawat S.Map/Reduce：simplified data processing on large clusters［J］.Communications of the ACM，2008，51（1）：107-113.

［7］朱凯，万定生，程习锋.水利普查成果分析中数据立方体计算研究［J］.计算机与数字工程，2014，42（9）：1591-1594.

［8］Markl V，Ramsak F，Bayer R.Improving OLAP performancebymultidimensionalhierarchicalclustering［C］// Proc of IDEAS’99，1999：165-177.

［9］胡孔法，陈崚，顾颀，等.数据仓库系统中一种高效的多维层次聚集算法［J］.计算机集成制造系统，2007，13（1）：196-201.

［10］Stockinger K.Bitmap indices for speeding up high-dimensional data analysis［M］//Database and Expert Systems Applications.Berlin Heidelberg：Springer，2002：881-890.

［11］Chen Y，Dehne F，Eavis T，et al.Parallel ROLAP Data Cube Construction on Shared-Nothing Multiprocessors［J］. Distributed and Parallel Databases，2004，15（3）.

［12］You J G，Xi J Q，Zhang P J，et al.A parallel algorithm for closed cube computation［C］//Proceedings of the 7th IEEE/ACIS International Conference on Computer and Information Science（ACIS-ICIS），Portland，Oregon，USA，2008.Washington，DC，USA：IEEEComputerSociety，2008：95-99.

［13］李伟卫，赵航，张阳，等.基于Map/Reduce的海量数据挖掘技术研究［J］.计算机工程与应用，2013，49（20）：112-117.

［14］师金钢，鲍玉斌，冷芳玲，等.MapReduce环境下的并行Dwarf立方构建［J］.计算机科学与探索，2011，5（5）：398-409. DOI：10.3778/j.issn.1673-9418.2011.05.002.

［15］Sergey K，Yury K.Applying Map-reduce paradigm for parallel closed cube computation［C］//2009 First International Conference on Advances in Databases，Knowledge，and Data Applications.IEEE Computer Society，2009：62-67.

［16］陆嘉恒.Hadoop实战［M］.2版.北京：机械工业出版社，2012：2-3.

Parallel computation of shell fragments cube Map/Reduce-based.

TANG Shanshan，ZHU Yuelong，ZHU Kai

College of Computer and Information，Hohai University，Nanjing 210098，China

In the high-dimensional and dimension hierarchical big data materializing，this paper proposes an efficient parallel shell fragments cube construction algorithm using Map/Reduce framework.The algorithm achieves parallel building and querying of shell fragments cube.For each data partition，map process of the construction algorithm calculates all possible data unit or prefixB encoding；Reduce process aggregates to calculate the ultimate shell fragments and measure index table.Experiments show that the parallel shell fragments cube algorithm not only combines the parallelism and scalability of Map/Reduce framework，but also combines the compression strategy and inverted index structure of shell fragments cube.The parallel shell fragments cube algorithm can effectively avoid the explosion of data volumes while materializing high-dimensional data，and provides the quick build and query operations.

On-Line Analysis Processing（OLAP）；shell fragments cube；Map/Reduce；parallel computation

A

TP391

10.3778/j.issn.1002-8331.1502-0051

水利部公益性行业科研专项（No.201501022）。

唐珊珊（1993—），女，硕士研究生，主要研究方向：数据挖掘与知识发现；朱跃龙（1959—），男，教授，CCF会员，主要研究方向：数据挖掘与知识发现；朱凯（1990—），男，硕士研究生，主要研究方向：数据挖掘与信息系统。E-mail：tangshanshanz@126.com

2015-02-03

2015-04-22

1002-8331（2015）22-0124-06

CNKI网络优先出版：2015-07-24，http://www.cnki.net/kcms/detail/11.2127.TP.20150724.1549.002.html