最近邻作用项对一维分子链孤子激发的影响
王洪丽,陈 浩,王瑞强
(华南师范大学物理与电信工程学院,广州510006)
最近邻作用项对一维分子链孤子激发的影响
王洪丽,陈浩*,王瑞强
(华南师范大学物理与电信工程学院,广州510006)
在电-声相互作用的一维分子晶体中,电子不仅与在位格点上的声子有相互的作用,同时与近邻格点也存在着微弱的相互作用.为了更真实地求解出一维分子晶体系统的基态问题,以量子化Holstein模型为基础并考虑电子与最近邻格点上声子的相互作用项对其的修正,此时系统处于基态时的Hamiltonian量也发生了相应的改变.运用压缩-相干态展开法和能量极小值等原理,求解出处于基态时极化子系统所满足的非线性Schrödinger方程和对应的孤子解、基态能量.并讨论了最近邻作用项的强度对一维分子链孤子激发如孤子的波峰、波宽、稳定性和系统基态能量的影响.
Holstein模型;极化子;压缩-相干态展开法;孤子激发
一维原子与分子晶格模型的研究对物理理论发展及一维、准一维材料的应用贡献非常大,例如:纳米线体系的制备和研究[1]、DNA链中的一些动力学问题[2]和导电高聚物的研究[3-5]等.一维分子晶体的Holstein模型[6]是处理这种电子-声子耦合体系最具代表性的模型,它对一维极化子系统的研究起着重要的指导作用.人们在对一维分子晶体Holstein模型的深入研究中发现了许多的求解方法[7-11],如变分法及相干态法.随着研究的深入,人们对一维分子晶体中Holstein模型进行了修正,获得了一些更接近一维分子晶体的真实基态结果[12-13],但至今未能获得其真正基态,也就是我们所求得的只是一个近似解.
本文研究带修正项的一维分子晶体模型的孤子激发问题.该修正项在原有Holstein模型的基础上考虑了电子与最近邻格点上声子的相互作用项.我们采用量子化的、带修正项的Holstein模型,求出系统基态的 Hamiltonian量及其所满足的非线性的Schrödinger方程.采用压缩-相干态展开法[14]、连续性近似和能量极小值等原理,求解处于基态时极化子系统所满足的非线性Schrödinger方程和对应的孤子解、基态能量.并讨论电子与最近邻格点上声子的相互作用对孤子激发、孤子的波峰和峰宽、基态能量及晶格位移的影响.求解能量极小值(基态能量)时,必然要考虑到波函数须满足这一约束条件.本文采用拉格朗日乘数法求能量的极小值,发现用这种方法求能量最小值更为简便.
1 系统的Hamiltonian量及基态极化子方程
考虑电子与最近邻声子相互作用项的一维分子系统的Hamiltonian量为(按惯例取h=1,a=1,其中a为晶格常数):
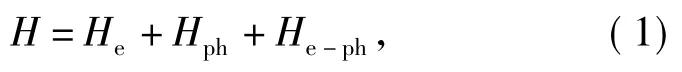
其中,
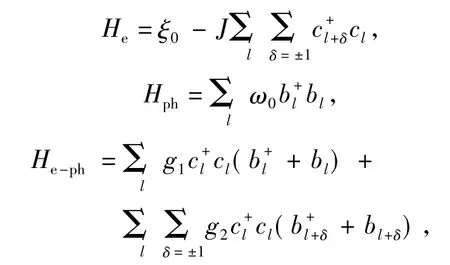

整个电-声系统的变分波函数可设为:
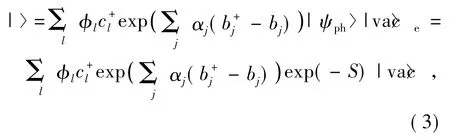
其中|vac〉ph、|vac〉e和|vac〉分别表示声子子系统、电子和电-声相互作用系统的真空态.为压缩算符,ρ为压缩参数,当ρ=0时,声子系统回到真空态.φl是电子出现在第l格点上的概率幅,满足.αj,φl是变分参数且都是实数.
将整个系统的波函数(3)和系统的哈密顿量(1)代入薛定谔方程H|〉=E|〉可得:
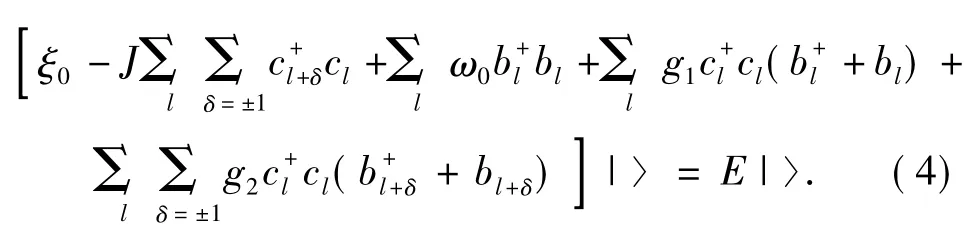
计算对应的能量本征值为:
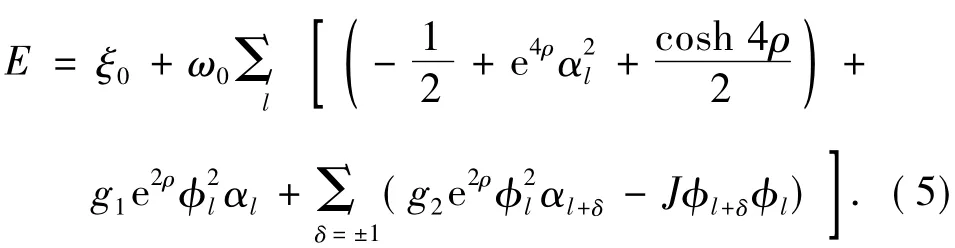
系统处于基态时,能量将取最小值,此时能量E的变分为0,又因φl满足归一化条件,即条件极值的问题,故采用拉格朗日乘数法求解基态能量.考虑到|g1|>>|g2|且|g2|<<1,可认为≈0,舍去.求得:

由于φl在整个分子链上是缓慢变化的,可以对φl采取连续性近似.则式(6)中第2个式子可化为:

2 极化子-孤子系统的基态孤子波解及系统的基态能量

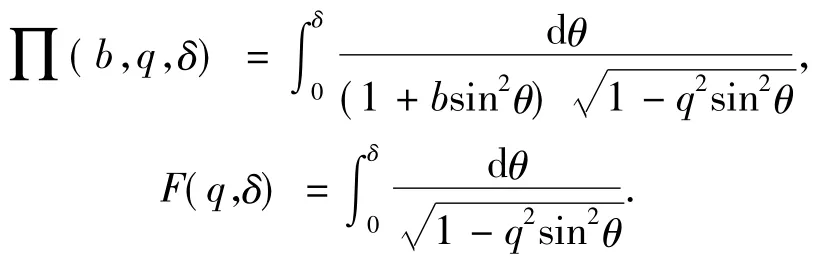
由于φ2<<1,所以可以近似把式中的第2项看作一个常数,并在等式右边的积分常数上.这样就得到了一个椭圆函数解,即:

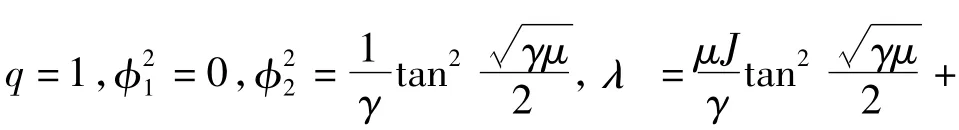
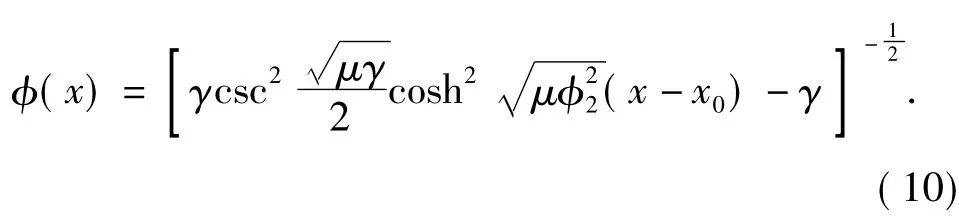
由此求得孤子的峰宽Ls和峰值Ps分别为:
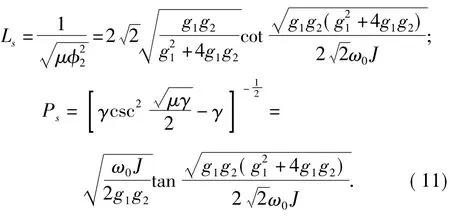
把以上结果代入式(5)中,求得处于基态时系统的能量为:
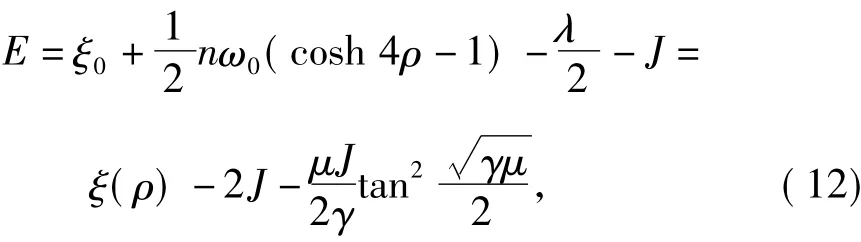
2.2当g1>0,g2=0时的求解

其中φ0(x)对应g2=0,即不考虑最近邻相互作用时,的孤子解、孤子的峰宽、峰值和基态能量.

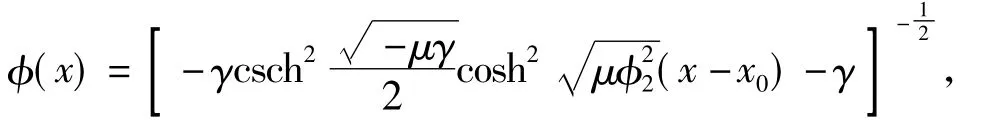
与之对应的孤子的峰宽Ls,孤子的峰值Ps和相应的基态能量E分别为:
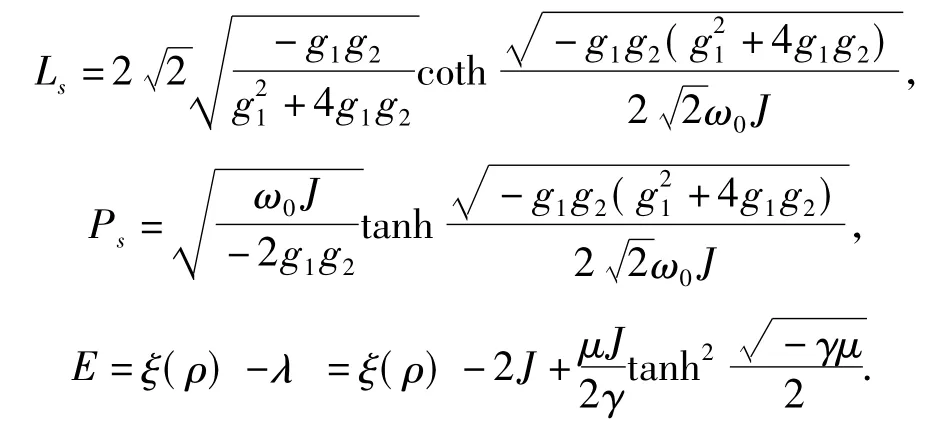
2.4当g1>0,<-0.25时的求解
3 结果与讨论
在电子-声子相互作用的一维分子晶体中,考虑电子与最近邻格点上声子的相互作用项(即g2/g1≠0),对量子化的Holstein模型进行的修正,计算出系统孤子激发的孤子解、峰值、峰宽及其对应的基态能量随最近邻相互作用项强度的变化关系(图1、图2),此处取ω0=J=g1=1.
当g2>0,可以看出随着电子与最近邻格点声子相互作用项系数g2的增大,孤子的峰值变大,峰宽变窄,孤子特征变的明显.此时的最近邻耦合项,增强了系统的非线性效应,使孤波的畸变增大,孤子能量更加的集中;
当g2<0时,随着相互作用项的增大,孤子的峰值变小,峰宽变宽,孤子特征越发的不明显.特别是在前文2.4中,g2≤-0.25时,波函数φ(x)=φ2是常数,系统不存在孤子激发.
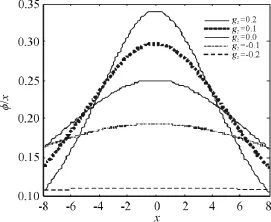
图1 g2取不同值时孤子的波函数图像Figure 1 The wave function images of soliton with different g2values
图2为孤子的能量、峰值、峰宽随耦合系数g2的变化.不难看出,随着最近邻作用项的变化,孤子的能量、峰值、峰宽也发生变化.当g2>0,随着耦合强度的增大,孤子系统的能量在减小,而峰值增大,峰宽减小;当g2<0时,随着耦合强度的增大,孤子系统的能量在增大,而峰值减小,峰宽增大.
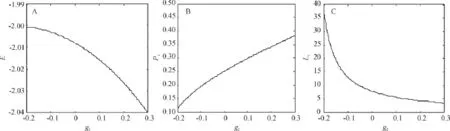
图2 (A)基态能量E、(B)孤子峰值Ps、(C)孤子峰宽Ls随g2的变化Figure 2 Changes of(A)the ground state energy,(B)peak of the soliton,and(C)width of the soliton with different g2values
图2仅考虑ω0=J=g1=1这一特殊情况,根据2.1、2.2和2.3的所得结果,结合式(7)可进一步讨论,当g2/g1>0时,较之与g2=0,孤子的峰宽减小,峰值增大,并且随着g2/g1比值的增大,孤子局域变小,孤子特征越来越明显,此时孤子系统的基态能比不考虑最近邻作用项的情况更负,孤子的稳定性增强,但由于能量的限制,将不利于孤子的激发;当g2/g1<0时,与g2=0的情况相比,孤子的峰宽变大,峰值减小,此时孤子局域变大,孤子能量增加,容易激发孤子,但不利于孤子的稳定性,且随着的增大,即最近邻作用项的反向增强,孤子特征越不明显.这里的最近邻作用项是一个弥散项,使系统的非线性效应减弱.特别的,当g2/g1≤-0.25时,孤子解变为φ(x)=φ2.此时方程的解为与横轴平行的一条直线,孤子特征完全消失.
为了更准确地描述分子晶格极化子系统的真正基态和相关的物理特性,本文在Holstein模型的基础上,考虑了电子与最近邻格点上声子的相互作用项.为了得到最优化的结果,变分波函数采用了压缩-相干态的办法.随着声子与最近邻作用项耦合强度的增大,最近邻作用项对一维分子链孤子激发的影响愈明显.现实中,这种耦合强度比较小,同时耦合强度和方式会受随着温度、电磁场、电子自旋以及原子的排列等因素的影响,在以往的模型中忽略它对一维分子链晶格的影响.随着对物理模型的精确程的严格要求,电子与最近邻格点上声子的相互作用项的影响不容忽视.
[1]Wan C C,Huang Y,Guo H.Dissipative quantum transport in a quantum wire[J].Physical Review B,1996,53(16):10951-10972.
[2]Shigaev A S,Ponomarev O A,Lakho V D.A new approach to microscopic modeling of a hole transfer in heteropolymer DNA[J].Chemical Physics Letters,2011,513(4):276-279.
[3]Lutchyn R M,Skrabacz J H.Transport properties of topological superconductor-luttinger liquid junctions:A real-time Keldysh approach[J].Physical Review B,2013,88(3):024511.
[4]Carosella F,Wacker A,Ferreira R,et al.One-dimensional massless Dirac bands in semiconductor superlattices[J].Physical Review B,2014,89(23):235301.
[5]Wazwaz A M.New(3+1)-dimensional nonlinear evolution equations with mKdV equation constituting its main part:Multiple soliton solutions[J].Chaos,Solitons& Fractals,2015,76:93-97.
[6]Holstein T.Studies of polaron motion:Part I:The molecular crystal model[J].Annals Physics,1959,8(3): 325-342.
[7]任学藻,廖旭,刘涛,等.一维分子晶体中的极化子[J].原子与分子物理学报,2006,23(4):616-620. Ren X Z,Liao X,Liu T,et al.Polaron of one-dimensional molecular crystals[J].Journal of Atomic and Molecular Physics,2006,23(4):616-620.
[8]江涛.一维分子晶体的极化子-孤立子运动[J].山西师范大学学报:自然科学版,2003,17(3):17-22. Jiang T.Polaron solitons motion in one-dimensional molecular crystals[J].Journal of Shanxi Normal University: Natural Science Edition,2003,17(3):17-22.
[9]赵翠兰,王丽丽,赵丽丽.有限深势阱里量子盘中极化子的基态性质[J].原子与分子物理学报,2013,30(4):637-641. Zhao C L,Wang L L,Zhao L L.The properties of ground state of polaron in quantum disk in finite depth potential well[J].Journal of Atomic and Molecular Physics,2013,30(4):637-641.
[10]任学藻,廖旭,黎雷,等.Holstein模型的一种新的近似方法[J].中国科学:G辑,2009,39(12):1716-1721. Ren X Z,Liao X,Li L,et al.A new approximating method for Holstein model[J].Science China Physics Mechanics Astronnmy,2009,39(12):1716-1721.
[11]Kalosakas G,Aubry S,Tsironis G P.Polaron solutions and normal-mode analysis in the semiclassical Holstein model[J].Physical Review B,1998,58(6):3094-3104.
[12]李琴兰,陈浩.关于修正的一位分子晶体模型的孤子解[J].原子与分子物理学报,2015,30(1):139-143. Li Q L,Chen H.An improved soliton excitation in the one-dimensional molecular-crystal model[J].Journal of Atomic and Molecular Physics,2015,30(1):139-143.
[13]Shen M,Li B L,Ge L J,et at al.Stability of vortex solitons under competing local and nonlocal cubic nonlinearities[J].Optics Communications,2015,338:1807-1811.
[14]Su X Y,Zheng H.Properties of the squeezed polarons on one dimension[J].International Journal of Modern Physics B,1998,12(7):2225-2232.
[15]刘式适,刘式达.特殊函数[M].2版.北京:气象出版社,2003:620-715.
【中文责编:谭春林英文责编:肖菁】
Effect on Soliton Excitation in One-Dimensional Molecular-Crystal Chain with the Nearest-Neighboring Interaction
Wang Hongli,Chen Hao*,Wang Ruiqiang
(School of Physics and Telecommunication Engineering,South China Normal University,Guangzhou,510006,China)
The electron-phonon coupling consists of the on-site electron-phonon interaction and the neighboring inter-site one as the electron should interact with its neighboring local phonons in the one-dimensional molecular-crystal model.In order to give more accurate solution,the effect of the nearest-neighboring interaction based on the quantized Holstein model is studied.Correspondingly,the Hamiltonian of the ground state is modified and then soliton excitation is improved too.By using the squeezed-coherent state expansion method and the energy minimum principle,the nonlinear Schrödinger equation for the one-dimensional molecular-crystal model is proposed,and then the solution and the ground state energy are obtained.Compared with the consequence neglecting the nearestneighboring interaction,the solution of the nonlinear Schrödinger equation changes and the ground state energy of the polaron are more negative with the augmentation of the nearest-neighboring interaction.
Holstein model;polaron;squeezed-coherent state expansion method;soliton excitation
O481.1
A
1000-5463(2015)03-0034-05
2014-07-01《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n
国家自然科学基金项目(11174088)
陈浩,教授,Email:chenhao@scnu.edu.cn.

