基于遗传算法与灵敏度分析的误差分配方法研究*

金增楠，王 军，，吴文嘉，舒启林

（1.沈阳建筑大学机械工程学院，沈阳 110168；2.沈阳理工大学机械工程学院，沈阳 110159）

基于遗传算法与灵敏度分析的误差分配方法研究*

金增楠1，王 军1，2，吴文嘉1，舒启林2

（1.沈阳建筑大学机械工程学院，沈阳 110168；2.沈阳理工大学机械工程学院，沈阳 110159）

为节约制造成本，故在设计阶段根据机床结构，合理分配机床产生的几何误差，从而减小相邻部件间误差累积。以TX1600G镗铣加工中心镗削系统为研究对象，首先结合多体系统理论建立镗削系统空间误差模型并通过该模型推导出误差累积公式；其次在其基础上导入各部件几何误差，通过数值计算与理论分析得到相关部件的误差灵敏度系数，基于此系数提出一种误差分配原则；最终应用遗传算法验证其准确性，该方法也同样适用其它多轴机床误差分配研究。

灵敏度；遗传算法；误差分配

0 引言

随着机床精度要求的不断提高，零部件几何误差间的耦合作用所形成的空间误差已成为影响床身自身精度及加工工件精度不可忽略的误差因素之一。目前，机床企业在设计阶段采用传统类比、查询手册、设计者估计等相对落后的方法，设计的产品也依赖设计者经验，没有一种科学化、数字化、系统化的分析体系。故如何通过定量的方法确定机床各部件几何误差对机床整机精度的影响程度从而合理的进行机床精度分配是机床厂面临的重大难题［1］

目前，国内外解决此类问题方法有：算法分配法、微分分配法、解析分配法等对误差灵敏度和误差分配进行研究。算法分配法［2］如：遗传算法、Pareto算法等，此类算法首先通过齐次矩阵导出各部件空间误差，其次进行空间误差运算，得到空间误差累积公式，并且依据此公式对相应误差量进行加权求最小和，最后根据算法分配误差。但此方法因只是数值上追求最小值，没有考虑太多的实际问题。微分法［3-4］：该方法对误差累积公式进行偏微分求导，用求导所得系数表示各部件几何误差对整机精度的影响程度，但用此方法的文章都未定量分析出各部件分配误差量。解析法［5］：该方法是通过齐次坐标转换，用矩阵表达各部件几何误差对整机精度的影响程度，但此方法复杂繁琐，很难理解其矩阵表达的含义。

综上，本文在国家863计划重大项目“复杂箱体精密智能复合式镗铣加工中心的研发与开发”的课题背景下，本文以镗铣加工中心镗削系统为研究对象，综合上述方法的优缺点，采用齐次矩阵对镗削系统建立空间误差模型，根据镗削系统各部件之间的关系建立误差累积公式，依据此公式特性对各几何误差求导，得出相应的灵敏度系数，通过灵敏度系数分析得到最终各部件之间误差分配数值，最终使用遗传算法验证此结论。

1 TX1600G镗铣加工中心模型简介

TX1600G镗铣加工中心采用卧式镗削结构和龙门式铣削结构相复合的结构布局，镗削系统采用“箱中箱”结构，以最大限度减轻移动部件的质量和惯量，并提高机床整体刚性。

考虑工件和镗刀最终产生的空间误差及其累积过程，故把镗削系统划分为床身、滑台、滑枕、主轴、工作台、数控旋转台，如图1所示。床身包括底座和镗立柱，因在镗削系统运动过程中不产生相对运动，故视其为整体。若立柱产生的误差影响镗削系统精度，镗立柱可单独分析。

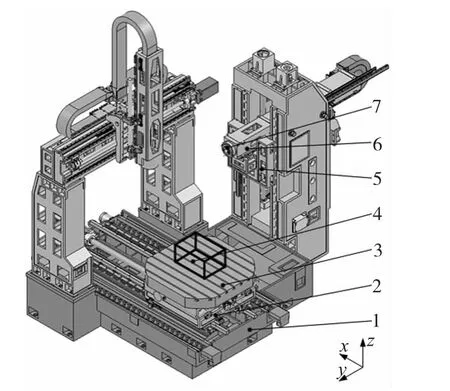
图1 TX1600G镗铣加工中心模型

2 镗削系统误差建模

2.1 结构简化

综上所述，可把镗削系统简化成如图2所示。

图2 空间坐标结构运动简图

其中01表示床身且与大地固定，02坐标系表示X向滑台在机床坐标系中沿X向移动，03坐标系表示数控旋转工作台可沿Z轴做（90°、180°、270°）旋转运动，04坐标系表示示例工件，05坐标系表示Z向滑台在机床坐标系中沿Z向运动，06坐标系表示滑枕在机床坐标系中沿Y轴运动，07坐标系表示主轴（包括刀具）绕滑枕做旋转运动。

2.2 特征方程

根据所简化的结构简图，可分析出各相邻体之间相对运动并依据此构建误差特征矩阵，设绕x轴得转角α、绕y轴的转角β、绕z轴的转角γ，矩阵中Sxz、Syz、Sxy为两轴间的垂直度；xij、yij、zij为x、y、z轴进给量，i，j∈（1～7）；△x、△y、△z为定位误差；△αij、△βij、△γij为两轴转角误差，i，j∈（x，y，z），其中T12i、T23i、T34i、T15i、T56i、T67i是理论值（只考虑单个自由度），T12p、T23p、T34p、T15p、T56p、T67p是实际值（考虑每个部件在空间产生多个自由度）。具体细节参见文献［7］。

2.3 误差累积公式

建立空间误差模型可以清晰的表达出每个部件在其自由度方向上产生的误差，但没能有效得表达出刀尖点最终产生的几何误差，基于此通过分析空间误差模型，可得到误差累计公式（13）～（19）。这些公式充分得表达出：①每个部件的误差对整个系统几何误差的映射关系；②可以系统的表达出几何误差最终影响参数以及产生的数值。

第一条工作链最终累积的位置误差为

第二条工作链最终累积的空间位置误差为

最终机床产生的位置误差：

3 工程实例验证

3.1 灵敏度分析

通过误差累积公式（13）～（19）可以观察出，该公式对于公式内任意误差呈一维线性关系，均可表达成：

此公式Y表示分别在x、y、z参考轴上形成的总误差，X表示具体每个误差项，k、b分别表示代入其它误差所得数值。依据线性方程的几何意义可知，k表示对Y递增（或者递减）程度的快慢，因几何意义故此处可表达对整体误差项的影响程度高低。

考虑文章篇幅的限制，仅列出部分零部件几何误差。

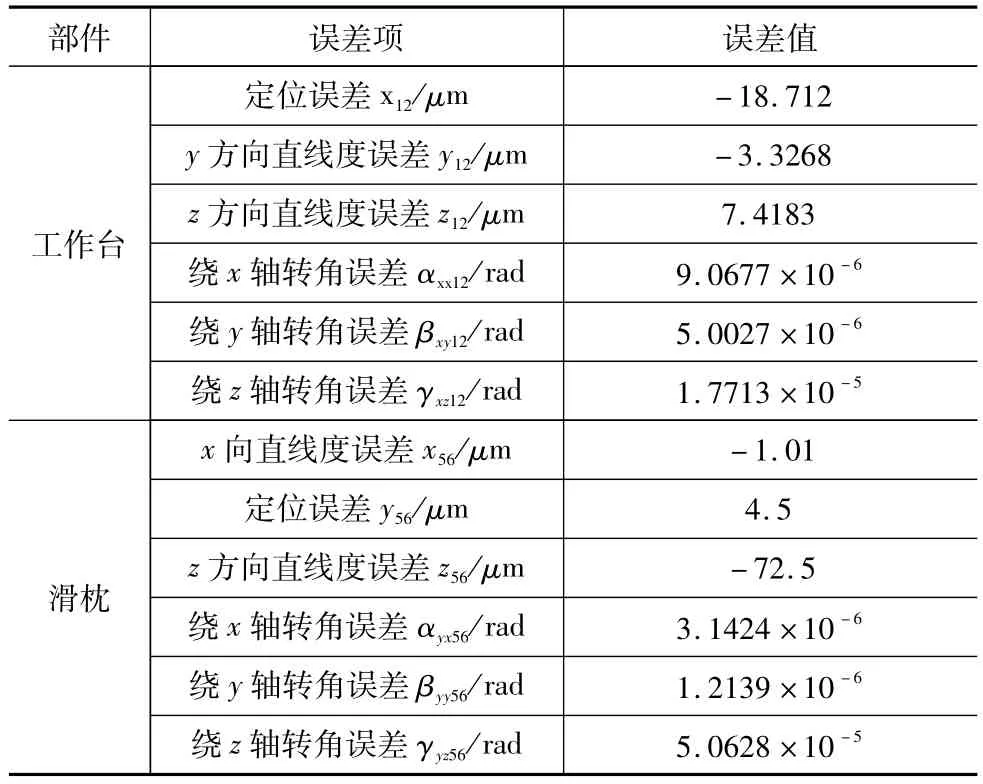
表1 TX1600G镗铣加工中心的几何误差值

将表1所示的几何误差以及其它部件几何误差代入公式11～16，最后由公式17可得在x轴上产生-10.9782μm、在y轴上产生-14.1542μm、在z轴上产生-61.475μm误差。然后将每个误差量设定自变量为X，镗削系统几何误差为因变量Y，导出公式如表2所示。

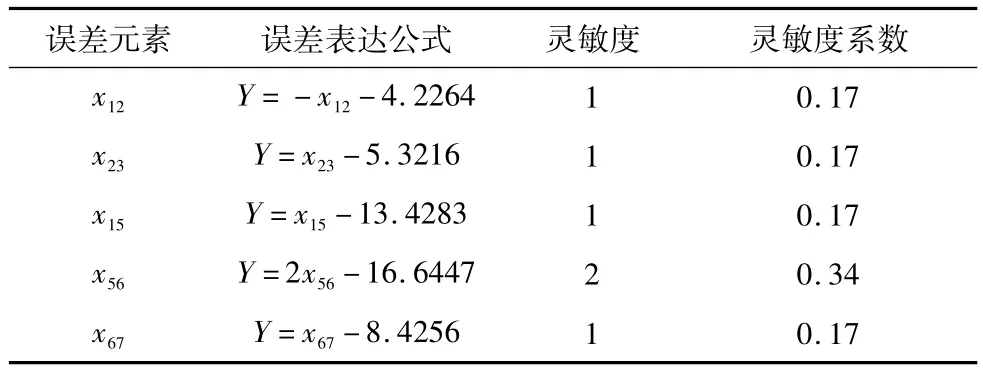
表2 X轴误差元素、灵敏度及灵敏度系数

本文以各部件作用在x轴上的直线度误差为例进行误差分配，其它轴误差分配原则与此分析方法一样，不再重复叙述，如表2所示数据中因转角所导致的直线度误差数量级在10-4μm，故在计算中忽略其对直线度误差的影响，因而导致自变量的系数都是整数。

如表2所示可以观察出x56所代表的滑枕灵敏度系数最大，说明其对镗铣系统整体几何误差影响程度比较高，根据设计经验以及对零件加工准确性，不易对灵敏度高的部件进行大范围误差调节，因此可依据灵敏度系数大小反向调节。如表3所示。

表3 基于灵敏度分析对X轴误差分配

3.2 遗传算法验证

因误差分配方法实验的复杂性和可操作性不强，故采用遗传算法验证，其利用自身简单编码和比较优越的繁殖机制表达复杂现象的优点，已解决此类问题。本文根据遗传算法的优越性，对误差分配值进行预测，用预测结果与实际分配值进行比对，验证实际分配的正确性。

应用MATLAB遗传算法工具箱，具体步骤及参数如下：

（1）编写M文件@myobjfun1：

functiony=myobjfun1（x）；Y=0.22*（x（1）ˆ（-2））+0.23*（x（2）ˆ（-2））+0.22*（x（3）ˆ（-2））+0.11*（x（4）ˆ（-2））+0.23*（x（5）ˆ（-2））；

（2）采用Double vector（浮点数编码）；

（3）Creation function（创建函数）选择Uniform，创建具有均匀分布的随机初始种群；

（4）Population size（种群规模）取100；

（5）采用Stochastic uniform Selection（随机均匀排序法）进行选择操作；

（6）在Reproduction（复制）中，将70个个体保留在下一代；

（7）采用Heuristioc Crossover（启发式交叉法），进行交叉操作，取交叉概率pc=0.75；

（8）适应度函数为目标函数，可以表达成：

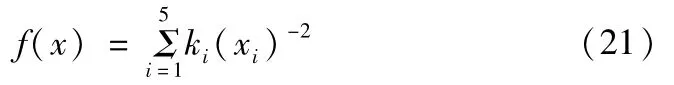
其中ki表示权数，1～5表示本次统计五个部件的几何误差，xi表示具体误差。其结果如图3所示。

图3 基于遗传算法对X轴误差分配结果

根据图3显示，最终方程最小值为0.012972μm，设定xm代表通过MATLAB而分配所得的误差项，其分别是：xm12=8.3518μm、xm23=9.3123μm、xm15=10.0246μm、xm56=-6.4215μm、xm67=9.7203μm。但依据公式（13）～（19）所示，实际误差在x轴上产生-10.9782μm，依据MATLAB中相关参数的对比，重新分配其误差结果，对基于灵敏度分析的误差分配结果与MATLAB预测误差分配结果进行对比，如表4所示。

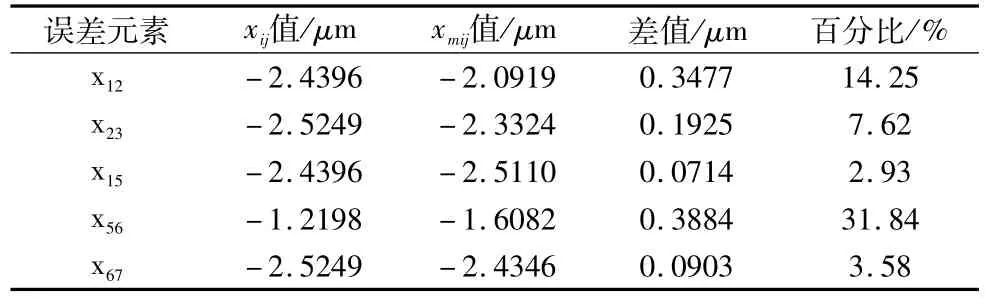
表4 两种误差分配理论比较

根据表4所示：xij表示基于灵敏度误差分配值，xijm表示基于遗传算法误差分配值。其中误差元素x12和x56两次分配值偏差百分比分别是14.25%和31.84%，相比其它误差元素波动过大。原因：①从图3可以观察出遗传算法有突变点，并且突变点具有无法预测的随机性，目标函数f（x）达到最小值时，在局部领域内有可能产生微小突变，使得两者误差相差过大。②灵敏度分析考虑了各部件之间的关系以及对镗削系统几何误差影响程度的关系，而遗传算法中目标函数的权数大多采用经验数值，没有考虑太多实际情况，这也将导致数值上出现偏差。

据表4中误差元素x23、x15、x67两种方法所产生的偏差百分比在10%以内，因机床精度在3～5μm，10%的偏差表示控制偏差在0.2μm左右，足够满足前期设计者对机床精度要求，且通过遗传算法的验证也可说明基于灵敏度分析法的误差分配原则的可行性。

如果有外购件，像旋转工作台和主轴，其在x轴上的误差分别是x23、x67，此类误差因外购件拆装的复杂性和操作性不强的特点，故变成装配误差，在装配过程中可以通过刮研装配体之间接触面以达到精度要求。

4 总结

（1）在建模过程中，根据4×4阶矩阵表达的实际意义和具有相对运动相邻低序体之间的运动原理，建立误差模型。为TX1600G镗铣加工中心的误差测量及具有相似工作原理的几何误差检测提供理论公式。

（2）在设计阶段，由于采用灵敏度分析方法进行误差分配，故可反复修改相关部件结构，使其系统几何误差接近或者达到机床设计者要求。两者分配法比较，偏差不超过0.2μm，说明基于灵敏度分析误差分配法具有一定的正确性，且此方法考虑机床自身机构特点比遗传算法更具优越性。本文所采用的方法实现了从经验公式到理论推导的转换，为精密机床制造提供了重要依据。

（3）在装配阶段，可以根据相应结论对各部件进行误差分配以达到精度要求，但若有外购件时，如本文中x23所代表的旋转工作台和x67所代表的主轴，可针对其结构特性，在不影响使用精度的情况下，改变相邻部件间接触面，以最终实现补偿措施。

［1］杨枝.高档数控机床几何误差建模与参数溯源优化技术及其应用［D］.杭州：浙江大学，2014.

［2］康方.数控机床制造精度的优化分配方法的研究［D］.北京：北京工业大学，2008.

［3］Chen G，Liang Y，Sun Y，et al.Volumetric error modeling and sensitivity analysis for designing a five-axis ultra-precision machine tool［J］.The International Journal of Advanced Manufacturing Technology，2013，68（9）：2525-2534.

［4］程强，刘广博，刘志峰，等.基于敏感度分析的机床关链性几何误差源识别方法［J］.机械工程学报，2012，48（7）：171-179.

［5］Lee R S，Lin Y H.Applying bidirectional kinematics to assembly error analysis for five-axis machine tools with general orthogonal configuration［J］.The International Journal of Advanced Manufacturing Technology，2012，62（12）：1261-1272.

［6］Ahn K G，Cho DW.An analysis of the volumetric error uncertainty of a three-axis machine tool by beta distribution［J］.International journal of Machine tools and Manufacture，2000，40（15）：2235-2248.

［7］栗时平，李圣怡.三轴机械几何误差辨识新方法的研究［J］.中国机械工程，2002，13（21）：1818-1820.

［8］张虎，周云飞.基于激光干涉仪的数控机床运动误差识别与补偿［J］.中国机械工程，2002，13（21）：1838-1841.

［9］黄强，张根保，张新玉.机床位姿误差的敏感性分析［J］.机械工程学报，2009，45（6）：141-146.

［10］李小力.数控机床综合几何误差的建模及补偿研究［D］.武汉：华中科技大学，2006.

［11］沈金华.数控机床误差补偿关链技术及其应用［D］.上海：上海交通大学，2008.

［12］Wu Z，Xu C，Zhang J，et al.Modal and harmonic reponse analysis and evaluation of machine tools［C］//Digital Manufacturing and Automation（ICDMA），2010 International Conference on.IEEE，2010，1：929-933.

［13］袁哲，赵汉驰，许丽娟.直齿轮振动传递误差可靠性及其敏感度［J］.沈阳建筑大学学报（自然科学版），2013，29（4）：739-743.

（编辑 赵蓉）

Research on Method of Error Distribution Based on Genetic Algorithm and Sensitivity Analysis

JIN Zeng-nan1，WANG Jun1，2，WU Wen-jia1，SHU Qi-lin2
（1.School of Mechanical Engineering，Shenyang Jianzhu University，Shenyang 110168，China；2.School of Mechanical Engineering，Shenyang Ligong University，Shenyang 110159，China）

In order to save the cost of machinery，in the design stage the geometric errors generated by the machine are distributed reasonably in accordance with the machine structure，thus the accumulation of errors between adjacent parts is reduced.Based on the boring systemof TX1600G boring-milling machining center，combining multi-body system theory，model of volumetric errors for the boring system is established and accordingly formulas of cumulative errors are calculated in the first place.Secondly import geometric errors of components onto which you build formulas.With calculating and analyzing to get error sensitivity coefficient of related components，based on this kind of error distribution coefficients are proposed principle.With application of genetic algorithms to verify the accuracy of the method and this way is applicable to what analyzes other multi-axis machine error of error distribution in the final.

sensitivity；geneticalgorithm；error distribution

TH161；TG536

A

1001-2265（2015）06-0044-05 DOI：10.13462/j.cnki.mmtamt.2015.06.013

2015-01-31；

2015-02-25

国家863计划重大项目（2012AA041303）；辽宁省科技计划项目（2013220017）

金增楠（1989—），男，吉林东丰县人，沈阳建筑大学硕士研究生，研究方向为数字化设计制造与应用，（E-mail）syljzn@163.com；王军（1956—），男，辽宁丹东人，沈阳理工大学、沈阳建筑大学教授，博士生导师，研究方向为先进制造技术，（E-mail）wangjun@sjzu.edu.cn。