基于极值符号序列分析的EMD端点效应处理方法*

徐卓飞， 刘　凯

（西安理工大学机械与精密仪器工程学院 西安，710048）



基于极值符号序列分析的EMD端点效应处理方法*

徐卓飞1， 刘凯1

（西安理工大学机械与精密仪器工程学院 西安，710048）

针对经验模式分解（Empirical mode decomposition，简称EMD）的端点效应提出一种新的抑制方法。考虑到极值序列在EMD分解的包络线形成中占有主导地位，将信号局部极值序列进行符号化，根据符号特征进行特征匹配，在信号两端依据符号序列特征匹配结果进行符号序列拓延与对应信号还原，对拓延还原后的信号进行EMD分解以实现端点效应抑制。笔者所提方法对于随机信号与周期信号都有着明显的抑制效果，通过对仿真信号和轴承故障信号端点效应的分析验证了方法的正确性。研究与ARMA模型、BP神经网络、镜像拓延等常见方法进行了对比，笔者所提方法的各分量有效值指标均值为19.64％，低于其他方法，说明对低频分量有着更好的抑制效果。

经验模式分解；端点效应；信号拓延；波形特征匹配；符号序列

引 言

经验模式分解于20世纪90年代由Huang等［1-2］提出，它是一种具有自适应性的时频分析方法，可根据信号的局部时变特征进行自适应的时频分解，将信号分解成若干个本征模式分量（Intrinsic mode function，简称IMF），每个分量反映出信号的一种特有频率信息。EMD具有良好的高频分辨率与自适应性，若对IMF分量进行Hilbert-Huang变换获取Hilbert谱，可准确描述信号的能量随时间和频率的变化规律，相关研究内容已广泛应用于图像处理技术、机械测试与故障诊断、材料结构损伤检测、地球物理学等领域。

在机械故障诊断中，振动信号是最主要的特征来源，EMD与H HT变换对于振动信号的特征提取有着非常重要的意义，但由于其采用了三次样条曲线进行插值，使得信号端点处极值点不确定，信号两端往往会产生发散现象。随着分解过程逐步进行，这种发散会逐渐向内污染整个信号序列，进而使分解结果失真并失去实际意义，这就是所谓EMD的端点效应，对于较短低频信号序列影响尤为明显［3-5］。

在EMD的实际应用中，需要有效地抑制端点效应，同时还应该兼顾信号本身的趋势，避免扭曲信号端部的特征，Huang等在提出EMD方法的同时，还提出了根据特征波对原始数据进行延拓以抑制端点效应的方法，该特征波是由信号两端2个连续的极值点及其频率与幅值所决定，该方法已申请了专利［6］。近年来相关学者对此问题进行了深入研究，一般认为端点效应的抑制需要合理有效地拓延信号，目前主要拓延方式有信号序列拓延、极值点拓延、镜像拓延等：杨建文等［7-8］利用时变参数（ARMA）模型对信号进行了预测和拓延，类似方法对于随机性较强的信号效果较差，受限于模型复杂度和参数的不确定性［9］；Cheng Junsheng等［3］利用支持向量机对信号序列进行了边界的拓延，但支持向量机参数和核函数的变化会影响结果，规律并不易掌握［10］；蔡艳平等［9］结合混沌相空间重构理论，提出一种基于改进型Lyapunov指数边界拓延方法，对于无规律具有混沌特征的非平稳信号端点效应抑制更具优势；除了拓延方法外，祁克玉等［11-12］提出了基于余弦函数窗的端点效应抑制方法，通过余弦窗与原信号的内积运算，对信号两端处进行处理，这样一来保留了内部大部分信号的正确性，因此在低频段分量进行分析时，该方法的效果优于信号拓延法，但对较短信号存在局限性，在一定程度上改变了原有的信号；杨斌等［4］利用标准互相关函数对信号进行拓延，由于拓延信号保持了原始信号的内部特征，取得了很好的效果，其研究针对包络线进行特征匹配，未从信号本身出发。在实际应用中，计算效率是不能忽略的重要因素，特别对在线信息处理、信号分析等问题，信号拓延的计算效率偏低。因此王学敏等［5］提出了极值平移法，考虑到信号局部极值对于拓延影响效果最为明显，提出直接利用两端极值进行拓延，提高了计算效率，但由于忽略了信号内部序列，误差会增大。从上述研究内容发现，信号拓延依然是抑制EMD端点效应最为普遍的方法，但其中仍存在如下问题：信号拓延则多以信号自身为匹配对象，这样不但匹配计算量增加，也容易受信号局部异常点的干扰；由于不同信号的周期性与长度都存在较大差异，不同拓延方法往往具有一定的局限性。

考虑到极值序列在EMD包络线形成中起到主要作用，提出了一种基于符号序列分析的信号拓延方法，以实现端点效应抑制，该方法具有以下特点：a.由于仅对极值特征分析，计算效率会相应提高；b.适用于周期与非周期信号，不受信号长短的限制，只需调节匹配所用符号特征长度即可实现调节。主要研究内容包括：信号极值序列的符号化、符号化序列的特征匹配、符号序列拓延与信号还原等。拓延信号以原始信号的极值为预测基准，在保证极值走势正确的前提下，忽略了局部细微变化对于信号拓延的干扰。最后通过仿真混叠信号、轴承故障信号进行了方法的验证，并在此基础上实现了基于EMD与HHT相关特征集的故障模式聚类分析。

2 EMD端点效应分析

EMD分解主要过程如下［1］：a.确定信号x（t）的局部极大值序列和局部极小值序列，分别记为xmax和xmin；b.依据xmax和xmin确定信号x（t）的上下包络谱及局部均值m（t）=（xmax+xmin）/2；c.信号与局部均值的差记为h1（t）=x（t）-m（t），若h1（t）符合IMF条件，则将其作为x（t）的第1个IMF分量，若不满足条件，则使x（t）=h1（t），重复上述步骤n次，直至得到第1个基本模式分量c1（t）；d.分解出第1个基本模式分量后，从x（t）中减去c1（t），得到剩余值序列r1（t）=x（t）-c1（t）。重复上述步骤，依次继续获得第2、第3个基本模式分量，记为c2（t），c3（t）等，最后原始信号剩余部分为rn（t），则有

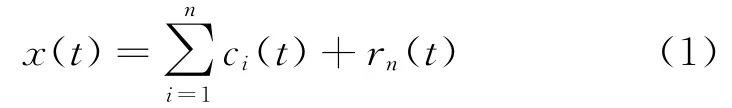
其中：ci（t）为EMD分解得到的各个IMF；rn（t）为信号分解后的余项；i和n为分解次数。以上步骤b中局部均值是通过对信号极值点进行样条插值后求均值得到，因此在插值时，上下包络线两端并不是由信号数据确定，从而产生信号两端包络线发散的现象，进而产生数据拟合的误差；步骤b～d中逐步分解IMF分量的过程中，每次误差都会累积，逐步向信号的内部以及低频分量传播，使频率较低的分量最终失去实际物理意义。

3 基于符号序列分析的端点效应处理方法

信号拓延是抑制端点效应的主要方法，但一般拓延方法不注重信号的大尺度特性，更强调对局部进行预测分析，这样易被信号中携带噪声干扰，从而影响分解结果；考虑信号的EMD是以局部极值为基准展开的，拟将符号化信号的优点引入极值分析，通过极值的符号化序列特征匹配实现信号拓延，之后再进行EMD与HHT变换从而抑制端点效应。

符号时间序列分析是从符号动力学理论、混沌理论以及信息理论基础上发展起来的一种分析方法，它根据一定规则的阈值函数，对时间序列进行离散处理，将不同的数值序列转化为相异的符号序列［13-15］。所提出端点效应抑制方法技术路线如图1所示，主要包括原始信号的极值符号化、信号两端的符号序列匹配搜索与拓延、拓延序列还原等内容。

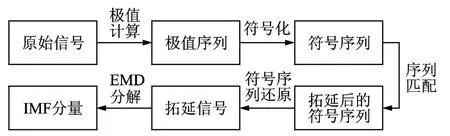
图1　基于符号序列分析的EMD分析流程Fig.1 The analysis process of EMD based on symbol sequence

3.1原始信号的极值序列符号化

在EMD分解中，极值点对于信号包络线有着非常重要的影响，针对极值拓延可提高计算效率［5］。在以极值为主要特征进行拓延之前，对其进行符号化处理，以消除局部变化对特征的影响，以保证信号趋势预测的准确性，选取最为常见的均值二进制序列进行符号化。

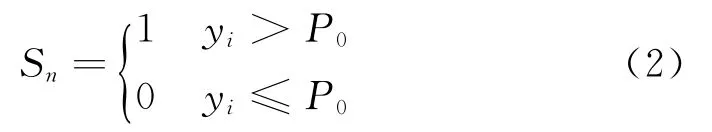
极值序列符号化过程如图2所示。首先，获取信号的极值序列，将原始信号｛xn｝的局部极大值和局部极小值提取出来组成极值序列｛yn｝，对其进行二进制符号化，以获取反映时序信号大尺度特征的符号统计特征值，并且降低噪声对信号的不良影响，在二进制符号化过程中以均值为界，转化规则为极值序列｛yn｝经过转换成为二进制符号序列｛Sn｝，分别划分为两种符号模式0和1，由于0和1是原始信号局部最大值、最小值和均值之间相互大小关系的体现，这样就从一个基于局部极值的角度获得了信号变化趋势，忽略了其余信号点，故称其为体现大尺度变化特征。由于振动信号中的确定信号对应的符号编码呈现大概率值，而随机噪声对应的符号编码呈现小概率值，故这种编码方法可以减小信号中随机噪声的影响从而捕捉信号中大尺度特点。

完成均值符号化后，需要先将｛Sn｝划分为短序列后再进行编码，若符号序列长度为L，将由N个0或1连续构成的单元称为一个基本编码单元，详细过程如图2所示。如式（3）所示

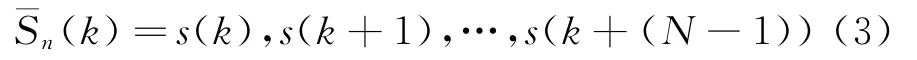
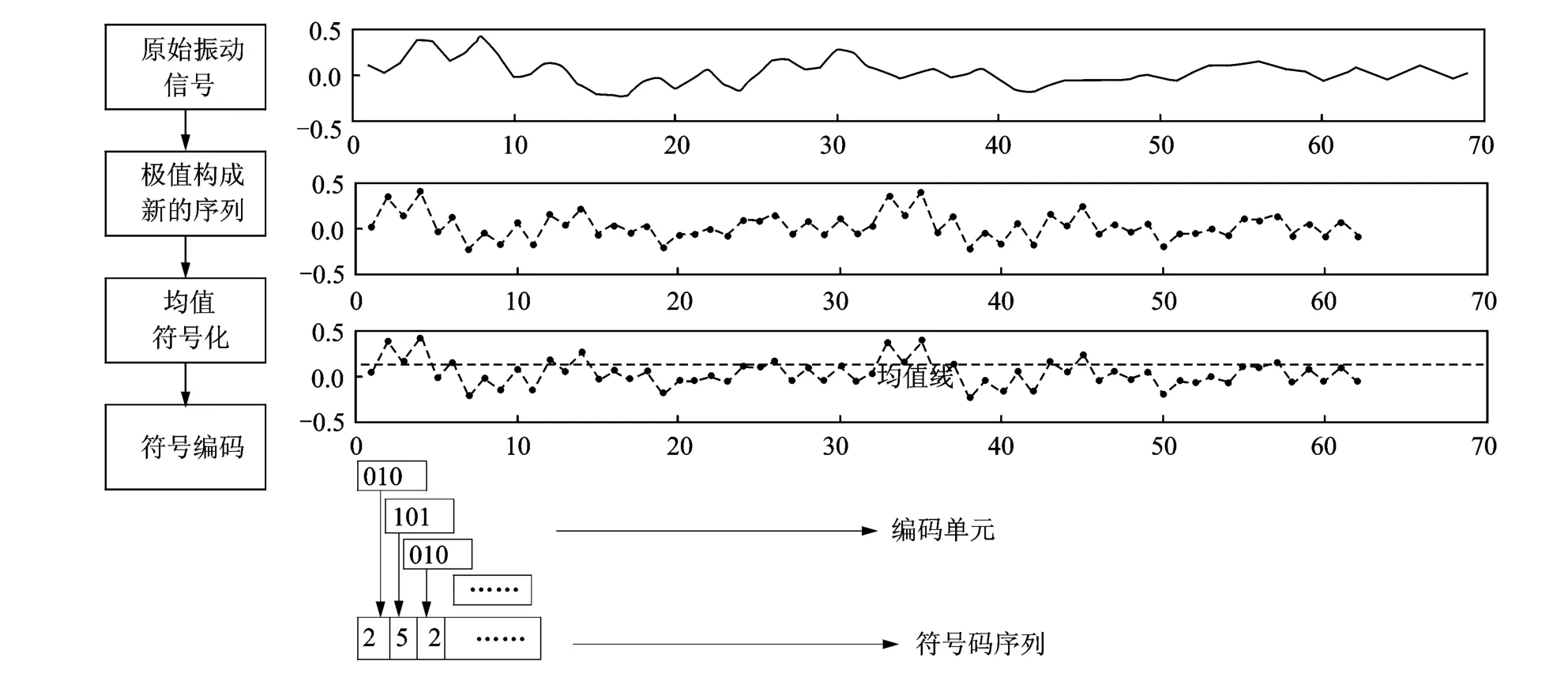
图2　原始信号的极值序列符号化Fig.2 The extreme symbolization of original signal sequence

其中：k=1，2，…，L-（N-1）。

由于振动信号中的确定信号对应的符号编码呈现大概率值，而随机噪声对应的符号编码呈现小概率值，这种编码方法可以减小信号中随机噪声的影响从而捕捉信号中大尺度特点。N的长短选取不同，会影响所提取特征符号是否能够更精确地描述信号，对于同一个信号而言，N越小则编码基本单元越短、编码位数越长，更突出局部特征；N越大则编码基本单元越长、编码位数越短，更突出整体特征。根据符号化研究内容：进行符号化变换所获得的符号序列可以较好地区分原时间序列中的确定结构和动力学噪声，当Shannon熵有最小值时所确定的段符号序列长度L为最佳，为满足这一要求并结合相关研究文献，选N=3时满足信号拓延要求。编码过长过短都会导致计算复杂、特征不突出、编码失效等问题［16-17］。

3.2符号序列的匹配与拓延

标准互相关函数通过对连续信号点的计算，可以描述两段相同长度不同的信号间的相关性，若相关性越高则认为其两端变化趋势越接近，所对应的匹配系数也就越小，故本研究选取标准互相关函数作为依据。将极值符号序列两端边缘处序列分别截取下来，依次与整个序列进行匹配，以标准互相关函数作为判定函数，若w0（x）为从符号序列两端截取的匹配符号序列，将其和其余符号序列依次进行匹配，每次匹配选取相同长度序列wi（x），记m为w0（x）与wi（x）长度。为了有效地获取信号的周期性特征，对于周期信号而言，m应当大于信号一个周期所对应的符号编码序列长度；对于非周期信号而言，m应当大于实际零件或设备的一个工作周期中所采集的信号对应的符号编码长度；此外，匹配长度需要考虑符号序列本身长度，如果匹配长度较短，考虑的点较少则导致预测可靠性低，反之则可靠性高，但是选取过长则会导致无法匹配。依次计算w0（x）与wi（x）之间的匹配系数c，如式（4）所示

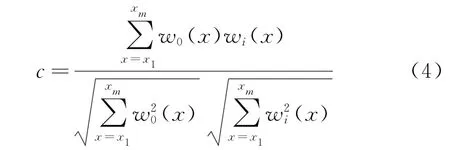
根据互相关函数性质，当c最小时匹配符号序列w0（x）与整个序列中某一段wmin（x）最为接近；之后，选取wmin（x）前后的序列对原序列进行拓延，将两端拓延序列还原为对应信号；对拓延信号进行EMD分解后，将各个分量两端拓延部分截去，即可获得较为准确的IMF分量。

研究所提出方法在符号化过程中强调了对极值点的控制，这样就忽略了信号非极值部分的变化，从极值序列变化对信号进行了匹配。本方法另一个特点是利用原始信号的某一段进行拓延，所以同时适用于周期信号和非周期信号。对于周期信号而言，所提出方法可根据其信号极值的周期性变化实现特征匹配，自动测量出信号的周期性并实现信号的正确匹配，可实现周期信号的准确拓延；对于非周期信号，由于该方法最终从信号本身选取一段进行拓延，具有较强的可靠性。

4 周期信号分析

对于周期信号式（5）而言，其由3个余弦信号组成，其频率分别为50，100和200 Hz，具体如图3所示，其中采样数据点长度为1 024。

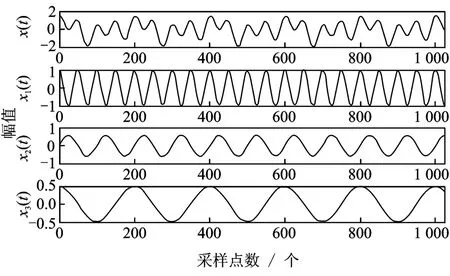
图3　信号x（t）及各分量信号Fig.3 The signal x（t）and its components

直接对信号x（t）进行EMD分解，结果如图4（a）所示，对比原始信号分量，分量IMF1-3边缘处都发生了严重的失真；图4（b）是经过端点效应抑制的结果，各个分量的边缘发散现象明显得到消除，信号更加接近原始分量；c（t）是余项，其大小程度则反映了信号EMD分解之后产生的累积误差，可以发现经过拓延后的信号余项远小于直接分解的余项。

通过对比仿真分析发现：由于所提出拓延方法对信号的结构进行了匹配，所以可以准确拓延周期信号，起到端点效应抑制效果，这是非拓延类端点效应抑制方法所无法做到的。故本方法在针对周期信号处理上具有优势，且受信号长短约束较小［10-11］，只要目标信号的长度包含一个周期即可准确拓延。

图4　信号IMF分量的拓延对比Fig.4 The contrast of IMFs with signal extending

5 工程信号分析

实际工程中遇到的机械振动信号往往会体现出一定的周期性，但局部又存在很强的随机性，为证明所提出方法的可靠性，与相关EMD端点效应进行了对比试验，以实际轴承故障信号为研究对象，所用工程信号数据来自美国Case Western Reserve University电气工程实验室的滚动轴承故障数据库。

轴承型号和实验参数列于表1中，其中轴承损伤通过电火花加工在其外圈、内圈和转子上。图5为实验装置，滚动轴承安装在马达驱动的旋转机械系统上，将振动加速度传感器垂直固定在感应电机驱动端支撑轴承上方机壳进行数据采集。

表1　实验参数Tab.1 Experimental parameters

图5　实验装置Fig.5 Experimental device

5.1工程信号对比分析

对正常工作状态下轴承信号进行拓延与EMD分解，图6对比了抑制端点效应前后效果。图6（a）是不经端点效应抑制而直接得到的IMF分量；图6（b）是按文中方法处理后的结果，发现图6（a）中高频分量IMF2和IMF4分量的两端产生了明显发散现象，图6（b）中相应位置的发散现象则得到了很好的抑制。

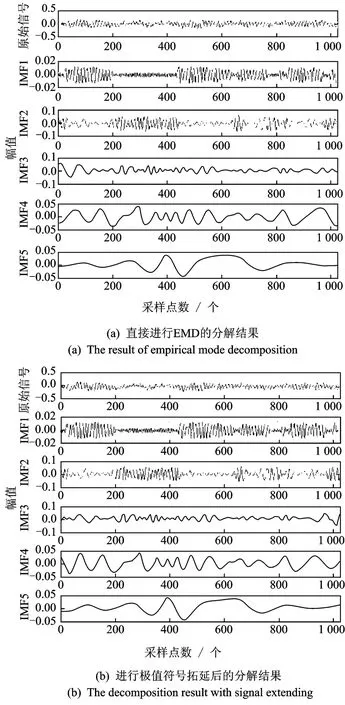
图6　正常轴承的EMD分解结果Fig.6 The decomposition result of normal bearing

为证明笔者所提出方法的正确性，将其与镜像拓延、ARMA预测拓延、SVM信号预测等几类常见方法进行了对比。为了评估端点效应对IMF的影响程度，采用一种基于能量的评价指标［5］。先计算原信号和各个IMF的均方根有效值RMS，如式（5）

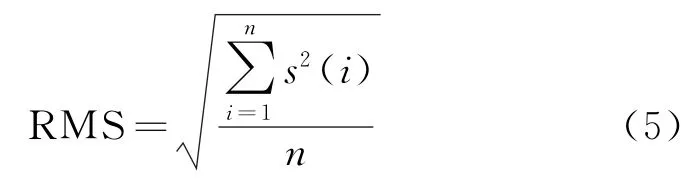
其中：RMS为信号有效值；s（i）为信号序列；n为信号采样点数。

计算各个IMF分量有效值RMSi与原信号有效值RMSre，计算其评价指标θi，如式（6）所示

其中：θi为第i个IMF的评价指标，

若端点效应对EMD没有影响，则θi=0；θi越大说明端点效应对该IMF影响越大。

对于实际工程信号而言，不可绝对准确地获得其IMF真实分量，故先将整个较长的原始信号进行EMD分解，在截取其中一段采样长度1 024的信号作为研究对象，将原始信号各IMF分量与之对应部分作为其近似真实IMF分量。

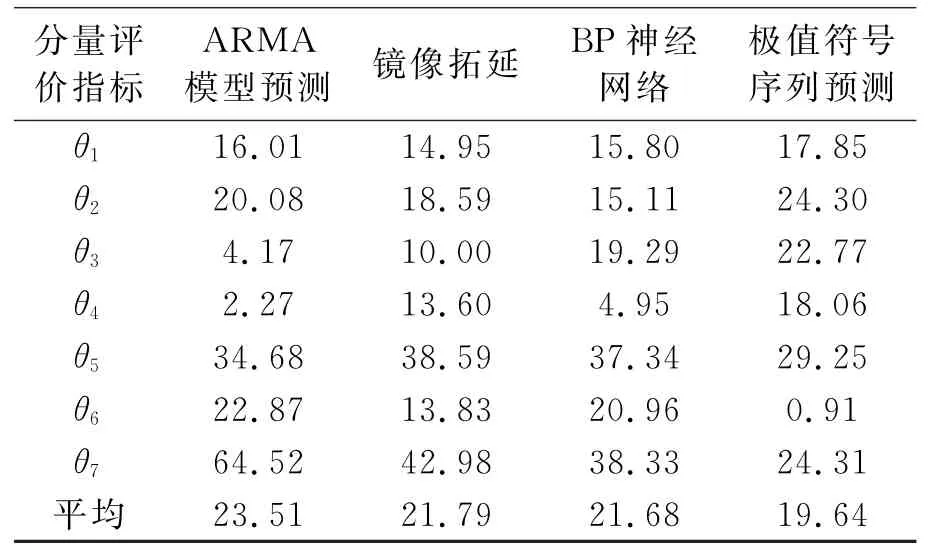
表2　评价指标的对比分析（％）Tab.2 Comparative analysis of evaluation indicator（％）

表2中记录了ARMA模型预测信号、镜像拓延、BP神经网络预测信号三种较为常见的EMD端点效应抑制方法，通过计算各个方法获取分量IMF1-7的评价指标θi，与笔者所提方法进行对比。

对比高频分量IMF1-3，发现各类方法都可以起到较好的端点效应抑制效果，相应的有效值评价指标θi在10％～20％的范围内，认为与真实信号相似度较高，各类方法差异不大，这与端点效应本身易于影响低频分量，对高频分量影响小有直接关系［5，7］。

相对而言，在低频分量IMF4-7中端点效应虽经过抑制但依然明显：ARMA模型的IMF7分量高达64％，低频分量IMF5-7失真较平均接近40％；镜像拓延与BP神经网络预测的结果中，近一半低频分量的θi值接近40％；而笔者提出方法各个低频分量的有效值评价指标最佳，其中IMF5-7均得到了最小的θi值且整体均值最小，故认为本方法失真度低，稳定性较好。此外，类似BP神经网络及相关方法，需要训练网络，对于工程信号而言，训练复杂度高，计算耗时长于本方法；类似笔者直接通过计算特征拓延的方法具有很强的普遍适用性。

5.2故障分类应用

通过实现轴承故障分类应用，验证提出方法的可行性和正确性：对轴承加速度信号进行拓延，将拓延信号进行EMD分解与HHT变换，依靠变换后所提取的特征集，进行聚类分析。实验选取了轴承的4种状态数据：a.正常；b.内圈故障；c.滚动体故障；d.外圈故障。按照表3计算IMF分量与其对应瞬时频率的统计特征值，重新进行聚类分析。图7是经过PCA聚类得到的结果，选取前两个主元，累积贡献率为99.83％。从图7中可见经过EMD与H HT变换所获取的基本统计特征集对于滚子故障有着较好的区分效果。

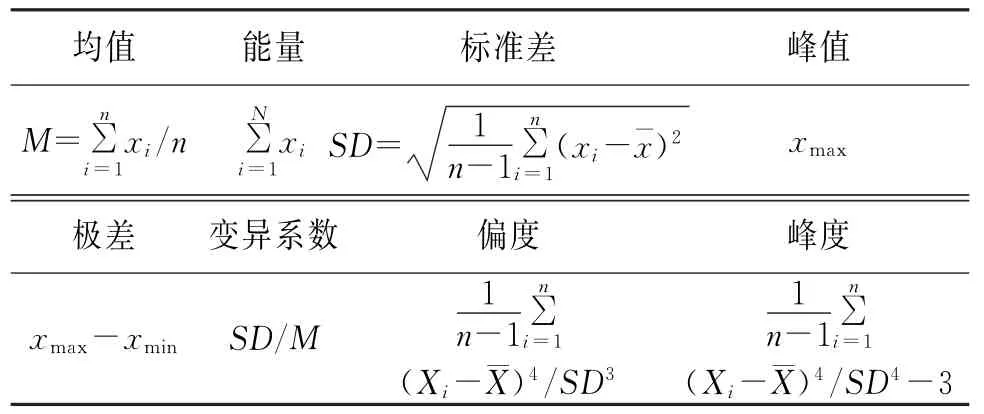
表3　所选取特征Tab.3 The selected features

图7　轴承故障PCA聚类结果Fig.7 The PCA clustering results of bearing failure

为准确评估分类效果，进行K均值聚类分析，选取每类轴承样本30个，共计120个，进行均值聚类，结果如图8所示。只有一个样本判断错误，其余全部正确聚类，结合本方法提取EMD特征能够准确实现轴承故障分类。

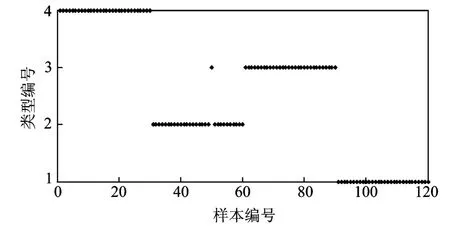
图8　K均值聚类结果Fig.8 The K-means clustering results of bearing failure

6 结 论

1）对仿真信号和工程信号进行了分析，相对于其他端点效应处理方法，极值符号序列分析同时对周期信号可实现无误差准确拓延；对非周期信号都有着很好地拓延效果，可有效抑制信号的发散现象，保持各个IMF分量不失真；试验验证了该方法对于各类信号有着较强的普适性。

2）通过与ARMA、BP神经网络、镜像拓延等常见方法对比，以各个IMF分量的有效值特征为评价标准，验证了笔者方法对低频分量处理的优越性；对实际工程信号进行分析，并提取EMD与H HT的相关特征集，实现了滚动轴承故障的准确聚类。

本方法重点考虑了信号的极值变化规律，同时适用于周期信号与非周期工程信号，可为EMD与H HT相关研究及应用的正确性提供新方法和保证。

［1］ Huang N E，Shen Zheng，Long S R.The empirical model decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society，Lond，1998，454（A）：903-995.

［2］ Huang N E，Wu M，Long S R，et al.A confidence limit for the empirical mode decomposition and hilbert spectral analysis［J］.Proceedings of the Royal Society，Lond，2003，459（A）：2317-2345.

［3］ Cheng Junsheng，Yu Dejie，Yang Yu.Application of support vector regression machines to the processing ofend effects of hilbert-huang transform［J］.Mechanical Systems and Signal Processing，2007，21（3）：1197-1211.

［4］ 杨斌，陈桂明，刘建友.基于标准互相关函数的经验模态分解端点效应处理方法［J］.机械工程学报，2013，49（5）：63-68. Yang Bin，Chen Guiming，Liu Jianyou.Method of empirical mode decomposition end effect based on standardized cross-correlation function［J］.Journal of Mechanical Engineering，2013，49（5）：63-68.（in Chinese）

［5］ 王学敏，黄方林.EMD端点效应抑制的一种实用方法［J］.振动、测试与诊断，2012，32（3）：493-497. Wang Xuemin，Huang Fanglin.Practical method to restrain the end effect of EMD［J］.Journal of Vibration，Measurement and Diagnosis，2012，32（3）：493-497.（in Chinese）

［6］ Huang N E.Computer implicated empirical mode decomposition method.Apparatus，and article of manufacture：U.S.Patent 6311130B1［P］.2001-10-30.

［7］ 杨建文，贾民平.希尔伯特-黄谱的端点效应分析及处理方法研究［J］.振动工程学报，2006，19（2）：283-287. Yang Jianwen，Jia Minping.Study on processing method and analysis of end problem of Hilbert-Huang spectrum［J］.Journal of Vibration Engineering，2006，19（2）：283-287.（in Chinese）

［8］ 程军圣，于德介，杨宇.Hilbert-Huang变换端点效应问题的探讨［J］.振动与冲击，2005，24（6）：40-42. Cheng Junsheng，Yu Dejie，Yang Yu.Disscussion of the end effects in hilbert-Huang transform［J］.Journal of Vibration and Shock，2005，24（6）：40-42.（in Chinese）

［9］ 曹冲锋，杨世锡，杨将新.一种抑制EMD端点效应新方法及其在信号特征提取中的应用［J］.振动工程学报，2008，21（6）：588-593. Cao Chongfeng，Yang Shixi，Yang Jiangxin.A new method for restraining the end effect of empirical mode decomposition and its applications to signal feature extraction［J］.Journal of Vibration Engineering，2008，21（6）：588-593.（in Chinese）

［10］蔡艳平，李艾华，石林锁，等.EMD端点效应的改进型混沌拓延方法及其在机械故障诊断中的应用［J］.振动与冲击，2011，30（11）：46-52. Cai Yanping，Li Aihua，Shi Linsuo，et al.Processing method for end effects of EMD based on improved chaos forecasting model and its application in machinery fault diagnosis［J］.Journal of Vibration and Shock，2011，30（11）：46-52.（in Chinese）

［11］Qi Keyu，He Zhengjia，Zi Yanyang.Cosine Window-Based Boundary Processing Methord for Emd and Its Application in Rubbing Fault Diagnosis［J］.Mechanical Systems and Signal Processing，2007，21（7）：2750-2760.

［12］祁克玉，施坤林，霍鹏飞，等.EMD端点效应处理在转子摩擦故障诊断中的应用［J］.振动、测试与诊断，2010，30（5）：492-495. Qi Keyu，Shi Kunlin，Huo Pengfei，et al.EMD boundary processing method and its application to friction fault diagnosis of rotor system［J］.Journal of Vibration，Measurement and Diagnosis，2010，30（5）：492-495.（in Chinese）

［13］Jaclson E A.Perspectives of nonlinear dynamics［M］. Cambridge，England：Cambridge University Press，1989：5-20.

［14］陈晓平，和卫星，马东玲，等.基于符号熵与支持向量机的滚动轴承故障诊断［J］.中国机械工程，2010，21（17）：2079-2082. Chen Xiaoping，He Weixing，Ma Dongling，et al. Symbol entropy and SVM based rolling bearing fault diagnosis［J］.China Mechanical Engineering，2010，21（17）：2079-2082.（in Chinese）

［15］Daw C S，Finney C E A，Tracy E R A.A review of symbolic analysis of experimental data［J］.Review of Scientific Instruments，2002，74（2）：915-930.

［16］Lehrman M，Rechester A B，White R B.Symbolic analysis of chaotic signals and turbulent fluctuations［J］，Physical Review Letters，1997，78（1）：54-57.

［17］赵建华，张雨.采用符号序列Shannon熵的机器信息提取方法［J］.武汉理工大学学报，2009，33（2）：321-324. Zhao Jianhua，Zhang Yu.Extracting machine information by Shannon entropy of symbolic series［J］.Journal of Wuhan University of Technology，2009，33（2）：321-324.（in Chinese）

TH17；TH165+.3

10.16450/j.cnki.issn.1004-6801.2015.02.030

徐卓飞，男，1985年12月生，博士生。主要研究方向为机械工程及精密仪器设计。曾发表《A method for the fault prediction of printing press based on statistcal process control of registration accuracy》（《Journal of Information and computational Science》2013，Vol.10，No.17）论文。

E-mail：xzf-34216606@163.com

*国家自然科学基金资助项目（51275406，51305340）；陕西省自然科学基础研究计划资助项目（2013JM7009）；陕西省教育厅科学研究计划资助项目（2013JK1030）

2013-11-23；

2014-09-03