追问“争议错题”，思辨“认识封闭”——从一道图像信息题的“争议”说起

☉江苏省海安县城南实验中学　刘东升

追问“争议错题”，思辨“认识封闭”
——从一道图像信息题的“争议”说起

☉江苏省海安县城南实验中学刘东升

刚刚过去的中考模拟测试中，笔者所在地区模考卷改编了一道选择题，考后个别同行指出这是一道“争议错题”，并在相关QQ群里引发热议，本文记录这次“民间教研活动”，并深入追问这道“争议错题”，与更多同行研讨.

一、“争议错题”及溯源

考题（2015年江苏省海安县中考模拟卷）小李与小杨从某镇初中出发，骑自行车沿同一条路行驶到县城图书馆，他们离出发地的距离S（单位：km）和行驶时间t（单位：h）之间的函数关系的图像如图1所示，根据图中提供的信息，有下列说法：

（1）他们都行驶了20 km；

（2）小李全程共用了2.5 h；

（3）小李与小杨相遇后，小李的速度小于小杨的速度；

（4）小杨“后发先至”，即出发得晚，却先到达目的地.

其中正确的有（）

A.1个B.2个C.3个D.4个

简解：只要对照图像容易确认说法（2）（3）（4）正确；说法（1）中如果不深入追问，也可很快根据图像得出两人的行驶路程都是20 km.从而选D.

追问：考题中“他们离出发地的距离S”是两点之间直线段的长度吗？小李在行驶过程中一定存在静止状态（或休息）？从图像可以确认小杨行驶路是20 km，但能否确定小李也行驶了20 km？

在回应以上追问之前，不妨先列举一些来源.溯源1：来自《义务教育数学课程标准（2011年版）》.例55小明的父母出去散步，从家走了20分到一个离家900米的报亭，母亲随即按原速返回.父亲在报亭看了10分报纸后，用15分返回家.下面的图形中哪一个表示父亲离家后的时间与距离之间的关系？哪一个图形是表示母亲的行走过程？

图1

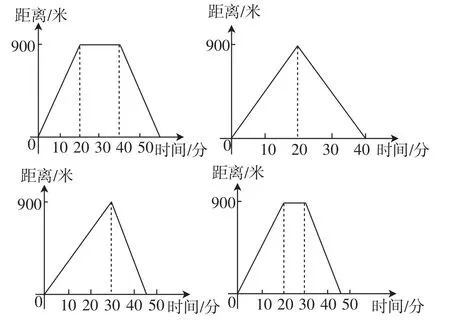
图2

溯源2：摘自人教版教材，八年级下册，第83～84页.

第9题下面的图像（如图3）反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后散步走回家.其中x表示时间，y表示张强离家的距离.根据图像回答下列问题：

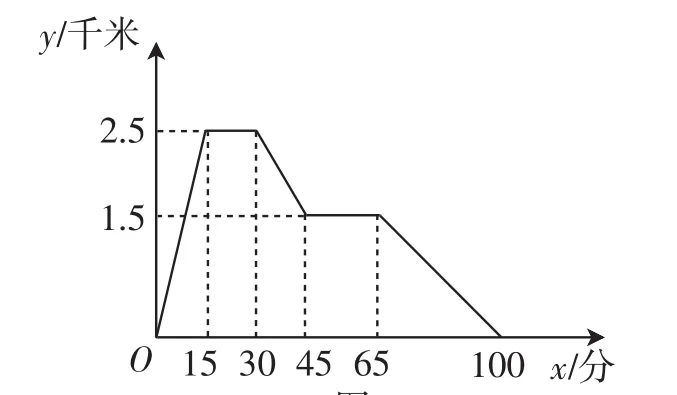
图3

（1）体育场离张强家多远？张强从家到体育场用了多少时间？

（2）体育场离文具店多远？

（3）张强在文具店停留了多少时间？

（4）张强从文具店回家的平均速度是多少？

第13题甲、乙两车从A城出发前往B城.在整个行程中，汽车离开A城的距离y与时间t的关系如图4所示.

图4

（1）A、B两城相距多远？

（2）哪一辆车先出发？哪辆车先到B城？

（3）甲、乙两车的平均速度分别为多少？

（4）你还能从图中得到哪些信息？

二、关于“距离”的相关认识

在QQ群的研讨过程中，不少老师提及距离的概念是“两点之间直线段的长度”，所以“考题”中使用距离是错误的，应该改为路程，或者约定它们在同一直线上.如果是这样的话，“课标（2011年版）”上列举的“例55”、人教版教材上的习题都是错误的？看来，我们需要对“距离”进一步认识，以下是经过网络搜索得出的关于“距离”的相关概念（维基百科）.

距离是一种标量，不具方向.这种量不会是负数.

在物理学上，距离是由某些媒介如人、动物和交通工具所经过路线的公里，由起点到终点的向量则是位移.

在数学上，距离是定义在向量空间中的一种函数.例如：日常生活中，最常见的距离就是欧几里德空间中的距离，是2阶范数；在图论中，距离是两个顶点之间经过最短路径的边的数目；在坐标几何中，距离是1阶范数.

而物体的路径是不具有方向性的标量，而路径长也需要基准点及参考点，但位移及路径长最大不同是路径长不具方向性.以白话来说，路径长可以是弯曲的，而位移却是一条线.

可以发现，争议考题是否为错题的焦点在于这道考题中的距离是物理学指出的“人所经过的路线的公里”还是数学上“最常见的距离就是欧几里德空间中的距离”呢？就考题、课标、教材上的“一脉相承”来看，它们似乎约定了“人所经过路线的公里”，这样来看，把思路引向欧氏几何中的距离确实不是一个好的解题念头.

三、想起“认识封闭”现象

关于“认识封闭”现象，罗增儒教授曾有精彩的阐释，下面稍作引述.

案例：如图5，表示某人从家出发任一时刻到家的距离（S）与所花时间（t）之间的关系，请根据图像编一个故事.

图5

很多人编写的故事都包括如下一些特征：

①在OP上作匀速直线运动；

②在PQ上静止；

③在QR上作匀速直线运动.

然而为什么“在PQ上静止？”到家的距离不变就是“到定点（家）的距离为定长（不变）”，这样的点一定是定点吗？这里的认识封闭在于：面对“到一定点的距离为定长”的数学情景时，只想到静止而想不到运动（轨迹！圆周运动，空间为球），数与形的双向流动不够通畅.从知识上看，可能还有“距离”与“路程”的混淆：随着时间的推移而路程不变，当然是静止，但随着时间的推移而距离不变，则可能是静止也可能是运动.

现在可以发现，这是“一个很普遍的认识封闭现象”（认识封闭1），并且当我们进一步问会有多少种运动方式时，也存在认识封闭现象，普遍没考虑到在圆周上既可以运动又可以静止，既可以前进又可以来回走动，既可以原路返回又可以另路返回（认识封闭2）.

到此，我们可以知道，提出上文那道考题是一道“争议考题”的同行应该是认识到了罗教授指出的“认识封闭”，从而认为说法（1）“他们都行驶了20km”出现了认识封闭！

可是据此认识封闭就认定考题有争议还为时尚早！如果确认“考题”中小李行驶的路线含有罗教授所指出的圆周现象的话，那么“考题”中还有“骑自行车沿同一条路行驶到县城图书馆”的条件，小杨行驶的也是小李的路线，他也应该出现类似的折线图像，然而从图像中看到的直线段来看，就会把前面分类讨论出来的路线中的圆周现象排除出去，问题又回到最初的简单状态.

四、相关感悟

上面概述了“争议考题”的疑点、溯源以及辨析，真理越辨越明，对争议考题的辨析、追问事实上也促进了我们深刻理解相关概念，并且获得如下感悟.

第一，对概念深入追问时需要注意不同阶段下的约定

由于混淆了不同阶段下的“距离”概念，导致人们对“考题”有了争议.然而这正是我们对科学概念深入追问时的一个注意点，即需要在不同语境中思考概念的意义，数学追求严谨，但又常常在深入追问中陷入尴尬，这也正是历史上几次所谓“数学危机”所带来数学发展的根本动力.类似的深入追问，还可提及三角形、四边形、圆的面积问题，根据定义，三角形是由三条线段首尾顺次相接组成的图形，线段源于直线，是没有宽度的，而求三角形的面积则是三角形围成图形的面积，四边形、圆的面积亦然.然而，我们不能求一个半圆的面积，因为半圆只是直径所对的一段圆弧.再比如，在七年级有理数一章中，数轴上的点与有理数是一一对应关系，而到后来数系扩充到实数系后，显然前面的表述是不严谨的.这样来看，“课标”“教材”等将“距离”混淆为“路程”就有了初级阶段的解释，也符合苏步青先生提出的“混而不错”的建议.

第二，充分肯定数学思维积极作用的同时，也要防止“数学的恶”

如郑毓信教授所指出的，“在充分肯定数学思维积极作用的同时，我们也应该清楚地看到这样两个基本事实：第一，思维方式的多样性.……第二，数学思维的局限性.”从这个意义上说，认真研究教材的内涵还应该包括如何读懂教材，即读懂教材背后欲言又止的含蓄和智慧，教材作为一种普适性的学习素材，有些知识在现阶段限于绝大多数学生的认知，可以也不必做深入追问时，教材上往往采取了上面提及的“混而不错”的模糊处理，如果教师出于个人喜好将深入追问的习惯传递给所有学生，其所带来的效果到底是积极的还是消极的，尚难定论.这方面的一个教学案例是：七年级上学期，为了说明所谓“负负得正”的正确性，不同版本的教材曾经采用“蜗牛爬行”“水位升降”等伪情境进行说明，意图向学生解释“负负得正”（本质上说是一种约定），还有人甚至从数学运算、运算通性的角度意图证明，然而效果均不理想.最新版人教课标教材又直接回归了一组算式的验算、发现与归纳“负负得正”，相对来说则是一种简明的、高效的处理方式，颇得一线教师认可.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.郑毓信.数学教师专业成长的6个关键词［J］.中学数学教学参考（上），2015（4）.Z

*本文为教育部教师教育国家级精品资源共享课立项建设课程“中学数学课程标准与教材研究”的成果（教师厅函［2013］2号：113）.