基于改进元胞遗传算法的蜗杆传动多目标优化设计*
基于改进元胞遗传算法的蜗杆传动多目标优化设计*
张 屹,余竹玛,郑小东,陈 平
(三峡大学机械与动力学院,湖北宜昌 443002)
建立了以蜗轮的齿冠体积最小、相对滑动速度最小和中心距最小为目标函数,以满足蜗轮蜗杆强度和刚度等条件为约束条件的多目标优化模型,提出了一种自适应差分进化的多目标元胞遗传算法。该算法针对多目标元胞遗传算法的特点,结合差分进化中不同进化策略的特性,将两种不同的进化策略融合为一种新的差分进化策略,得到一种参数自适应控制的多目标元胞差分遗传算法。将该算法同其他典型的多目标进化算法在标准测试函数上进行性能对比试验,结果显示所提出的算法相比其他算法具有更好的收敛性和分布性。工程实例的求解证明了该算法可有效解决相关实际问题。
元胞遗传算法;蜗杆传动;多目标优化设计
0 引言
蜗杆传动是一种以啮合形式的螺旋式传动,有着传动平稳、振动小、噪音低等优点,且具有自锁功能,被广泛用于各种机械设备中。一般情况下,设计蜗杆传动为类比法设计,其设计周期比较长,并且无法确定最终的方案是否是最佳方案,因此新的蜗杆传动设计方法就显得非常重要。
近年来,关于蜗杆传动的优化设计很多,文献[1]将蜗轮蜗杆传动优化设计处理成了单目标优化问题,无法获得综合性能最优的实施方案。文献[2]对蜗杆传动设计利用模糊理论来确定最优解,其结果易受到模糊准则选取的影响。文献[3]中的蜗杆传动的多目标优化问题的结果受到加权系数的影响。元胞遗传算法是一种适合求解多目标优化问题[4-5]的算法,文献[6]运用元胞多目标三维空间结构对机床主轴进行多目标优化求解,所得结果优于NSGA-II。本文利用改进的元胞遗传算法来求解蜗杆传动多目标优化设计问题,同时将结合不同的差分策略的特点,得到一种自适应差分元胞多目标遗传算法。将所得算法同其他经典多目标优化算法进行性能比较,最后将该算法应用于蜗杆传动的多目标优化设计,获得其Pareto前端曲线,同时与常规设计方案进行对比分析,进而验证算法的有效性,为蜗
杆传动的多目标优化设计提供一定依据。
1 蜗杆传动优化模型
1.1 设计变量的选择
蜗杆的传动的主要设计参数有蜗杆头数z1,模数m和蜗杆的分度圆的直径d1。因此选择X=为优化设计变量。
1.2 目标函数的建立

1.3 约束条件的确定
根据相关设计文献[2],蜗杆传动的优化设计需要满足以下约束条件。


2 改进的元胞遗传算法
差分进化[7]是由Storn和Price于1995年提出的一种基于种群的简单高效的全局优化算法,具有结构简单、容易使用、鲁棒性强等优点。差分进化算法中最重要的算子是差分变异算子,根据变异个体的生成方法不同,形成了多种不同的差分进化算子,其表示形式一般为“DE/a/b”,其中“DE”表示差分进化算法;“a”代表基向量的选择方式,一般有rand和best两种;“b”表示算子中差分向量的个数。在多个变异算子中,比较常用的有DE/rand/1和DE/best/1两个版本。在DE/rand/1中,待差分的个体是由种群中三个互不相同的随机个体组成,不需要任何适应值信息,有利于保持种群的多样性,因此其全局搜索能力较强,但收敛速度较慢。DE/best/1版本变异个体vti由xtbest作引导,因而其具有较强的局部搜索能力和较高的收敛精度,收敛速度也比较快,但算法陷入局部收敛的可能性也增大。根据这两种不同变异模式的特点,在算法中更希望把这两种变异模式进行折中,即在算法的进化前期以DE/rand/1为主,而在进化后期以DE/best/1为主,在变异算子中不仅考虑随机个体起的全局搜索的作用,也考虑最优个体所起的局部寻优的作用。为此,本文提出一种新的变异方案,其变异操作为:其中,λ∈[0,1]。从式(1)中可以看出,当λ=0时,该变异操作即为DE/rand/1方案,而当λ=1时,式(1)等价为DE/best/1方案。一般说来,优异的进化算法要求在进化初始阶段具有较强的全局搜索能力,以尽快地发现可能的全局最优解。而在进化后期,则要求具有较强的局部寻优能力,以提高算法的收敛精度和收敛速度。当λ由0逐渐递增为1时,xr1的权重逐渐减小而xbest的权重逐渐增加,从而可以保证算法既有较强的全局搜索能力同时又具有较快的收敛速度和较高的收敛精度,即在全局搜索和局部寻优之间达到平衡。为此,根据sigmoid函数来自适应调整参数λ,其表达式为:


这种自适应调整的原理来自于sigmoid函数。Sigmoid函数在线性与非线性行为之间显现出较好的平衡,拥有较平滑的顶部和底部,可以有效地保证全局搜索和局部寻优之间的平衡。
杂交算子把通过变异算子产生变异向量Vi,D=[vi,1,…vi,j,…,vi,D]与父个体向量Xi=[xi,1,…xi,j,…,xi,D]进行离散杂交得到尝试向量Ui=[ui,1,…,ui,j,…,ui,D]。具体方法为:对变异向量的每一维vi,j,生成产生一个[0,1]之间的随机数rand和[1,D]之间的随机整数jrand,如果rand<CR或者j=jrand,那么ui,j=vi,j,否则ui,j=xi,j,其具体表达式为:

在DE算法中有3个控制参数,即群体大小NP、缩放因子F和杂交概率CR。一般而言,这些控制参数会影响算法搜索最优解和收敛速度,如较小的F值会加速算法收敛,但容易使算法陷入局部收敛。现有的多目标进化算法中多采用固定的参数设置,难以满足多目标优化的需求。因此在本文算法中,结合模拟退火策略来自适应动态调整参数CR和F,其具体表达式如下:

式(1)~(5)中,t为当前进化代数,T为最大进化代数。相比基本差分策略,该策略具有如下特点:
(1)在算法的初始阶段,以全局搜索为主,有利于快速找到最优解,加快了收敛速度;
(2)在算法的后期,随着非支配解的增多,充分发挥最优个体的引导作用,有利于维持算法的多样性和局部搜索能力;
(3)该算子具有变异步长和搜索方向自适应能力,能根据不同目标函数场景进行自动自适应调整。
CombCellDE的原理图如图1所示。

图1 CombCellDE的原理图
首先将种群中的个体置于二维拓扑网格中,同时为每个个体分配邻居。针对当前中心个体,从其邻居中随机选择两个个体和从外部文档中随机选择一个个体作为待变异的四个父代个体,然后对这4个个体进行自适应的差分操作得到子代个体。如果子代个体优于父代个体,则用其替换掉当前中心个体同时将其加入外部文档中,如果父代个体和子代个体互不支配,则将子代个体加入邻居中,对邻居进行非支配排序操作并将最差个体放入外部文档中。其具体流程如下:
Step1:算法参数设置:种群规模N,最大迭代次数T,变异概率Pm,缩放因子F的上下限Fmax、Fmin和交叉概率的上下限CRmin、CRmax等;
Step2:设置迭代计数器t=0;
Step3:对每个个体按照本文提出的差分策略进行差分操作;
Step4:对得到的子代个体进行多项式变异操作;
Step5:评估子代个体,更新当前种群和外部文档;
Step6:更新计数器t,判断是否达到最大迭代次数。若是,则输入外部文档作为最优Pareto前端,否则转到Step3。
3 算法性能测试与分析
为了测试本文提出的算法在多目标优化问题上的性能,将本文提出的算法同NSGA-II[8]、MOCell[9]、CellDE[10]三种性能优异的的算法在ZDT[2]系列测试函数和两个约束测试函数上进行性能测试,并在相同的评价指标下对算法的优化性能进行分析。
3.1 算法性能指标
(1)收敛性指标(Epsilon)
假设Pareto前端集合为A,那么EPSILON指标[11]是移除A中每个个体所需要的最小距离的一个尺度。其具体形式是:假设,其中n是问题的目标维数:
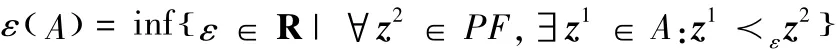
(2)分布指标(Spread)
Deb提出的分布指标[8]是衡量所得的Pareto前端解集的分布情况。其计算公式如下:

其中,di为所得Pareto前端上每两个连续解点的欧氏距离,¯d为这些欧氏距离的平均距离,df和dl分别为所得Pareto前端的边界点与Pareto最优边界点的欧氏距离,n是所得Pareto前端个体的数目。对于分布均匀的解来说,该指标取0。因此,该指标的值越小表明分布程度越均匀。
(3)超体积(Hypervolume)
超体积是用来计算获得的Pareto解集个体在目标域所覆盖的体积[12]。计算公式为:

式中,Q为所获得的Pareto前端的个数。对于这个Pareto前端中的每一个体i,vi是由参考点w=(0,…,0)和成员i所形成的超体积,此指标越大表明所得的Pareto解集能宽广地覆盖在其前端上。
3.2 测试结果与分析
上述四种算法均采用实数进行编码和多项式变异算子。NSGA-II和MOCell采用SBX交叉算子,CellDE是在MOCell的基础上用差分算子取代了SBX[13]交叉,其参数CR=0.1,F=0.5,CombCellDE采用上述的自适应差分进化算子,其CRmin=0.3,CRmax=0.8,Fmin=0.3,Fmax=0.8,。这四种算法的种群规模均为100,最大评价次数均为25000,交叉概率均为0.8,变异概率为1/len(len为决策变量的个数)。四种算法分别对测试函数进行30次独立运算,统计三个指标的平均值和方差,最优值用深灰色表示,次优值用浅灰色表示。

表1 分布指标平均值和标准差

表2 收敛性指标平均值和标准差
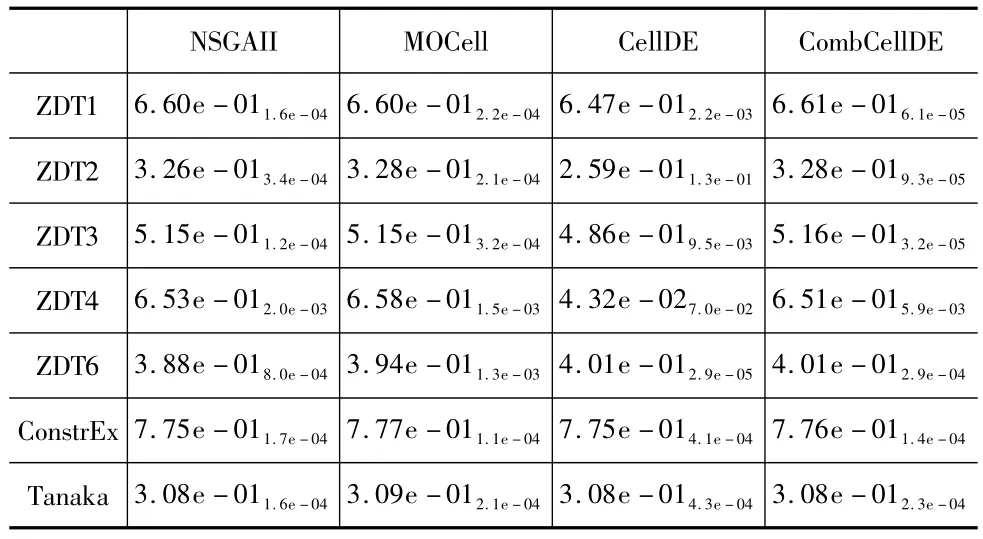
表3 超体积平均值和标准差
从表1的分布性指标来看,在7个最优值中,CombCellDE占了5个,MOCell占了2个,NSGA-II和Cell-DE均没有获得最优值。这表明CombCellDE所获得的最优前端的分布性最好,即分布得比较均匀。从表2的收敛性指标Epsilon来看,CombCellDE获得了5个最优值,MOCell获得了2个最优值,同时MOCell获得了5个次优值,NSGA-II获得了1个次优值。性能指标显示,CombCellDE在解决高维多目标函数时的收敛性要整体上强于其他三种算法。最后根据表3的综合性指标HV分析,CombCellDE获得了4个最优值,MOCell获得了3个最优值,NSGA-II和MOCell均获得了2个次优值,CellDE仅获得了1个次优值,由此表明CombCellDE在HV上的表现同在Spread和Epsilon上的表现是一致的。
4 工程实例求解
设计某减速器中的蜗杆传动,输入功率P= 10kW,蜗杆转速n1=1460r/min,工作模式为两班制,载荷较为平稳,传动比i=20,蜗轮齿冠所选用的材料ZcuSn10P1。要求对蜗杆传动优化设计,在保证蜗杆传动承载能力和强度的要求下,使蜗轮齿冠体积最小、传动效率最高和滑移速度最小。
针对上述实例,应用CombCellDE和CellDE进行求解。其参数设置如下:种群大小N=100,外部文档为100,最大评价次数Gmax=25000,变异概率Pm= 1/len(len为变量维数)。CombCellDE差分算子中CRmin=0.2,CRmax=0.8,Fmin=0.2,Fmax=0.8,CellDE中CR=0.5,F=0.5。由两种算法得到的Pareto前端如图2所示。

图2 两种算法得到的Pareto前端

图3 中心距与相对滑动速度关系曲线
为了能更清楚的显示各个目标之间的关系,图3给出了中心距和相对滑动速度的关系曲线。在图3中,处于左上方的Pareto前端的解说明其中心距较大同时具有较小的啮合面相对滑动速度,这表明蜗杆的中心距越大,其啮合面之间的相对滑动速度越小,传动效率越高。而对于处在右下方的Pareto前端的解,表明其中心距越小时,其相对速度越大传动效率也越低。由图3可以看出,针对中心距和相对滑动速度这两个目标,CombCellDE得到的Pareto前端要比CellDE得到的Pareto前端的分布更加均匀,并且也具有更好的收敛性。
综上所述,经过圆整,CombCellDE与CellDE相比,表现出一定的优势,将CombCellDE得到的Pareto前端的100个非劣解中单个目标最小的解同常规设计方案(z1=2,m=9,q=10)进行对比,其对比结果如表4所示。

表4 结果对比表
以第一个非劣最优解而言,相比常规设计,其齿冠体积减少了55.4%,传动效率提高了13.95%,中心距减少了7.09%。由此可见,采用CombCellDE对蜗杆传动进行优化,所得的最优方案更多,从而使得在满足承载能力及强度要求的约束下,蜗轮的齿冠体积更小、传动效率更高、中心距更小,整体结构较常规设计更为紧凑。
5 结论
将改进的差分进化算子融入到多目标元胞遗传算法中,提出了一种改进的自适应进化的差分元胞多目标遗传算法。该算法将差分进化的不同策略集成在一起,充分发挥
不同进化策略的特性,并且采用自适应策略,有效地提升了CombCellDE的收敛性和解集的分布性。性能测试结果表明,CombCellDE得到的Pareto最优前端更加逼近真实Pareto前端且分布均匀。应用该算法求解蜗杆传动的多目标优化设计,所得结果较常规设计有了一定的提高。该求解过程及优化设计结果表明该方法避免了常规设计中盲目选取参数的不足,具有一定的工程实用价值。
[1]贾毅朝,曲尔光,张慧鹏.基于MATLAB的蜗杆传动优化设计[J].组合机床与自动化加工技术,2010(5):97-99.
[2]曹蕾蕾,裴建中,张涛,等.基于PSO和模糊理论的蜗杆传动多目标优化设计方法[J].长安大学学报(自然科学版),2013,33(3):100-105.
[3]Nebro A J,Durillo J J,Luna F,et al.Mocell:A cellular genetic algorithm for multiobjective optimization[J].International Journal of Intelligent Systems,2009,24(7):726-746.
[4]Yuqiang Li,Shengming Liao,Gang Liu.Thermo-economic multi-objective optimization for a solar-dish Brayton system using NSGA-II and decision making.Electrical Power and Energy Systems,2015(64):167-175.
[5]姚金涛,林亚平,张明武,等.一种基于决策图贝叶斯网络的强度Pareto进化算法[J].计算机学报,2005,28(12):1993-1999.
[6]张屹,万兴余,郑小东,等.基于改进元胞多目标遗传算法的机床主轴优化[J].计算机工程与应用,2015,51(6):260-265.
[7]Price K V,Storn RM,Lampinen JA.Differential evolution,a practical approach to global optimization[J].2005,37-45.
[8]Deb K,Pratap A,Agarwal S,et al.A fast and elitistmultiobjective genetic algorithm:NSGA-II[J].Evolutionary Computation,IEEE Transactions on,2002,6(2):182-197.
[9]Nebro A J,Durillo J J,Luna F,et al.Mocell:A cellular genetic algorithm formultiobjective optimization[J].International Journal of Intelligent Systems,2009,24(7):726-746.
[10]Durillo J,Nebro A,Luna F,etal.Solving three-objective optimization problems using a new hybrid cellular genetic algorithm[M].Proceedings of the International Conference on Parallel Problem Solving from Nature.Heidelberg,Berlin,Germany;Springer-Verlag.2008:661-670
[11]Fonseca CM,Knowles JD,Thiele L,et al.A tutorial on the performance assessment of stochastic multi-objective optimizers[C].Third International Conference on Evolutionary Multi-Criterion Optimization,2005.
[12]Zitzler E,Thiele L.Multiobjective evolutionary algorithms:A comparative case study and the strength pareto approach[J].Evolutionary Computation,IEEE Transactions on,1999,3(4):257-271.
[13]Agrawal R B,Deb K,Agrawal R B.Simulated binary crossover for continuous search space[J].Complex Systems,1995,9:14-19.
(编辑 赵蓉)
M ulti-optim ization Design of W orm Transm ission Based on Im proved Cellular Genetic A lgorithm
ZHANG Yi,YU Zhu-ma,ZHENG Xiao-dong,CHEN Ping
(College of Mechanical&Power Engineering,Three Gorges University,Yichang Hubei443002,China)
Taking them inimization of the tooth crown of a worm wheel and the relative sliding speed transm ission efficiency and the distance from the center as objectives,established themodel for themulti-objective optimization under that the worm transmission meet the needs for strength and stiffness and others.An adaptive differential evolution of multi-objective cellular genetic algorithm was proposed.Considering the feature of different differential evolution strategies,a new differential strategy w ith parameter adaptive-controlwas formed.Aim ing at the characteristics of cellularmulti-objective optim ization algorithm,the new improved strategy was integrated into the algorithm.The comparative performance test results reveal that the proposed algorithm outperforms some state-of-the-art algorithms in terms of convergence and diversity.The engineering example proved the algorithm could solve the relevant practical problems effectively.
cellular genetic algorithm;worm transm ission;multi-objective optimization design
TH122;TG65
A
1001-2265(2015)08-0010-05 DOI:10.13462/j.cnki.mmtamt.2015.08.003
2014-12-01;
2014-12-30
国家自然科学基金(51275274)
张屹(1976-),男,兰州人,三峡大学副教授,博士后,研究方向为智能制造,系统优化设计,(E-mail)jxzhangyi1976@126.com。

