基于神经网络模型和网格变形技术的机床立柱优化设计研究*
王 亮,殷国富,谭峰,董冠华
(四川大学制造科学与工程学院,成都 610065)
基于神经网络模型和网格变形技术的机床立柱优化设计研究*
王 亮,殷国富,谭峰,董冠华
(四川大学制造科学与工程学院,成都 610065)
针对传统优化方法在大型复杂机械结构优化设计中的局限性和低效性,以及数控机床的轻量化设计要求,提出了一种基于BP神经网络模型和网格变形技术的大型复杂机械结构优化设计方法。对某型精密加工中心的立柱进行了有限元分析,建立了立柱优化的数学模型,引入网格变形技术,结合自行开发的VB软件,建立了立柱的参数化有限元模型。采用优化拉丁方实验设计方法,在设计空间中抽取样本点进行数值模拟,建立了由4个优化设计变量决定的多工况立柱导轨最大变形、立柱首阶固有频率和立柱体积的BP神经网络模型,并对建立的BP神经网络模型进行了泛化能力验证。采用多岛遗传算法,在保证立柱的动态特性基本稳定的前提下,对BP神经网络模型进行了轻量化优化设计。优化结果表明,在保证立柱多工况下导轨最大变形量和首阶固有频率基本不变的前提下,立柱体积减少2.4%,达到了机床轻量化优化设计要求。
立柱;神经网络;网格变形;多岛遗传算法
0 引言
在航空航天、船舶制造、精密模具以及汽车工业等制造行业领域里,精密卧式加工中心是关键的加工制造设备。在整个精密卧式加工中心的组成部分中,立柱是承载主轴箱、主轴及刀具等重要部件的支撑件,并承受加工过程中各种载荷,因此,立柱与整机性能密切相关,有必要对立柱进行结构优化。
对这类复杂的机械结构的优化方法研究,已经成为专家学者的研究的热点之一。文献[1]利用Workbench建立了立柱的筋板结构参数化模型,并对该模型进行了优化,该方法在建立立柱参数化模型时对立柱进行了过多的简化,没有真实地反映立柱的特性。文献[2]建立了某型磨床床身的参数化模型,并对参数化模型进行了优化。该方法在每次优化迭代后需重构床身参数化模型,并且建立复杂机械结构的参数化模型效率低下。文献[3]对床身筋板的不同布置形式对床身动态特性的影响进行了研究,该方法属于方案优选法,依赖于设计者的经验,效率低下。文献[4]利用响应面模型与遗传算法对机床立柱进行了优化,该优化方法在求解构建响应面模型需要的样本点时需要重构立柱CAD模型和CAE模型,效率还是不高。
针对上述问题,本文以某型精密加工中心的立柱为优化对象,提出了基于神经网络模型和网格变形技术的优化方法。
1 优化模型
本文以某型精密卧式加工中心立柱为优化设计研究对象,在满足实际边界条件的前提下,建立立柱的有限元分析模型并进行有限元分析,得到如下结论:在工作情况下,立柱的最大应力为4.87MPa,远小于材料的许用应力(120MPa)。大型机床立柱是典型的多筋板式零件结构,本文中的立柱主要有厚度为20mm、25mm和45mm三种类型的筋板,针对现代机床的轻量化设计要求,有必要对立柱筋板厚度进行尺寸优化。图1为立柱简化模型,图2为立柱内部筋板分布示意图。
根据上述分析情况,建立立柱优化数学模型:
(1)优化变量:

式中,X为图2所示立柱筋板厚度的增量值。
(2)目标函数:本文以立柱体积的最小化为目标函数。

(3)约束条件:

式中,Freq为立柱首阶固有频率下限,Disp1为工况1(主轴箱位于立柱导轨中部)立柱导轨最大变形量,Disp2为工况2(主轴箱位于立柱导轨下部)立柱导轨最大变形量。xiD(i=1,2,3,4)为优化设计变量下限值,xiU(i=1,2,3,4)为优化设计变量上限值。
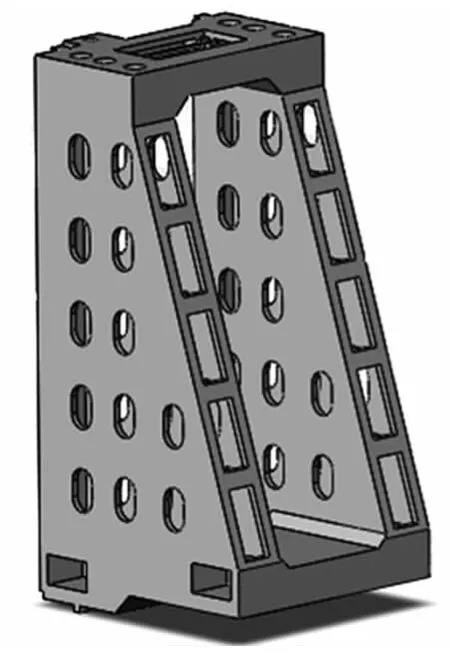
图1 立柱简化模型

图2 立柱筋板布局图
2 网格变形
传统优化设计方法中,每次在设计空间中取一组数据进行优化迭代后,都需要重新构建更新优化设计对象的CAD模型和CAE模型。优化设计对象为大型复杂的机械零部件时,无疑优化效率很低,本文引入网格变形技术解决上述问题。
CAE模型的网格变形通过给定的表述形式实现模型节点的移动,给定的表述形式可以是矩阵表示的数学形式,也可以是由目标形状定义的几何形式[5]。节点的移动包括平移、旋转和比例缩放等方式[6],由于本文中对立柱筋板厚度进行尺寸优化,因此采用节点的平移方式实现CAE模型的网格变形,节点的平移如图3所示。

图3 节点平移示意图
3 优化流程
基于神经网络模型和网格变形技术的优化流程如下,流程图如图4所示。
步骤1:对优化前的立柱划分网格和施加满足实际工作情况的载荷和约束,得到立柱的初始有限元模型,并对初始有限元模型进行求解。将得到的多工况下立柱导轨最大变形和立柱首阶固有频率作为参考,并确定优化模型约束条件的上下限值,建立立柱优化的数学模型。
步骤2:对立柱初始有限元模型需要优化的筋板节点集进行节点平移,得到立柱修改有限元模型。用自行开发的VB软件对立柱初始有限元模型和修改有限元进行对比处理,生成立柱参数化有限元模型。
步骤3:利用优化拉丁方采样方法在优化设计空间中选取样本点集,进行实验设计。
步骤4:利用步骤3中得到的数据集建立BP神经网络模型,并验证神经网络模型的泛化能力。
步骤5:利用多岛遗传算法对步骤4建立的BP神经网络模型进行优化。对优化得到的解进行数值求解,判断其是否满足优化要求和收敛条件。若满足,则优化完成;若不满足,则更新样本点集及BP神经网络模型,直到优化结果满足优化要求和收敛条件。
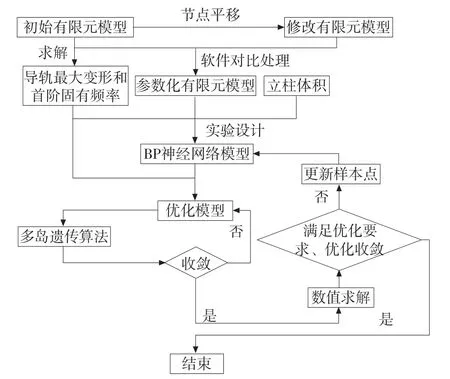
图4 优化流程图
4 BP神经网络建模
人工神经网络(ANN,Artificial Neural Network)是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型[7]。神经网络模型具有以下一些优点:①无须数学假设,具有黑箱特点;②学习速度快,具有极好的泛化能力;③具有较强的容错功能,即使样本中含有“噪声”输入,也不影响网络的整体性能。
本文通过BP神经网络强大的非线性映射能力,无须任何经验公式即可通过网络训练自动建立输入数据和输出数据之间的非线性函数关系,建立机床立柱优化设计变量xi与立柱导轨最大变形,首阶固有频率和立柱体积的映射关系。
4.1 确定神经网络训练样本
样本数据选择的科学性及合理性,对神经网络模型的精度具有重要影响。要建立高精度的神经网络模型必须对设计空间进行合理均匀采样。本文采用优化拉丁方进行设计空间的采样,相比于随机拉丁方采样方法,优化拉丁方采样使所有的试验点尽量均匀的分布在设计空间(见图5),具有非常好的空间填充性和均衡性,试验点分布更加均匀[8]。
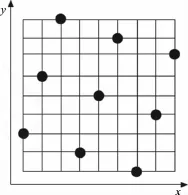
图5 优化拉丁方采样示意图
为了建立神经网络模型,最小采样数目为2N+ 1,其中N为优化设计变量的个数,在优化设计空间中采样数目越多,建立的神经网络模型精度越高。本文中有4个优化设计变量,最小采样数目为9个,为了保证建立的神经网络模型拥有足够高的精度,本文取24个样本,其中随机选取20个样本作为网络训练数据,其余4个样本作为测试数据。表1所示为样本数据。
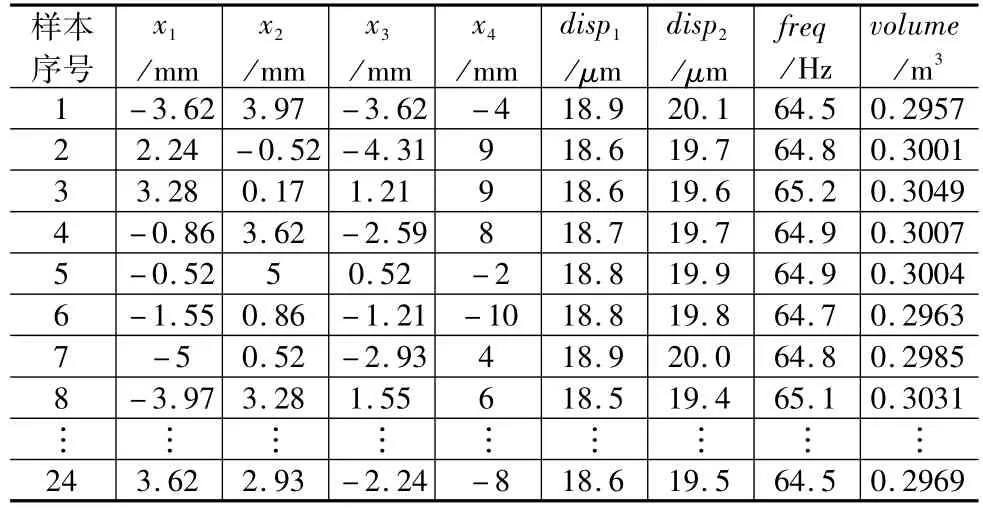
表1 网络训练样本数据
4.2 构建神经网络模型
BP神经网络是一种按误差逆传播算法训练的多层前向传播网络[7],是目前应用最广泛的神经网络模型之一。三层结构的BP神经网络可以任意精度逼近任意连续函数,因此本文采用三层结构的BP神经网络。网络输入层神经元个数为4,分别对应立柱优化设计变量xi( i=1,2,3,4),输出层神经元个数为4,分别对应于工况1下立柱导轨最大变形、工况2下立柱导轨最大变形、立柱首阶固有频率和立柱体积。
BP神经网络隐含层神经元个数对网络的精度有很大影响。隐含层神经元个数太多,将导致网络学习时间的增加,甚至可能出现“过拟合”现象;隐含层神经元个数太少,网络的精度不高,误差将变大,不能真实建立输入与输出的映射关系[9]。公式(4)为BP神经网络隐含层神经元个数设计经验公式,结合本文实际情况,将神经网络隐含层神经元个数设为可变值(取值范围为5~10),通过对具有不同隐含层神经元个数的网络进行误差分析(不同结构BP神经网络预测立柱体积误差见表2),确定最佳的网络隐含层神经元个数为5。
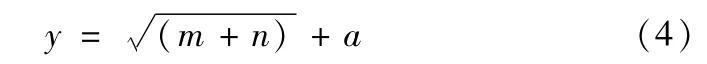
式中,y为神经网络隐含层神经元个数,m为神经网络输入层神经元个数,n为神经网络输出层神经元个数,a为取值范围为0~10的常数。
经过多次编程调试后确定:构建BP神经网络模型时,网络输入层与隐含层之间的传递函数采用sigmoid函数,网络隐含层与网络输出层之间的传递函数采用purelin函数,训练函数采用traingdm函数,神经网络学习速率设置为0.4,训练误差设置为0.001。
BP神经网络经过1155次训练之后,基本趋于稳定,网络误差为0.00099983,网络训练误差曲线如图6所示,并且得到各层的权值和阈值,目标函数如式5所示。

表2 不同结构BP神经网络预测误差 %

图6 BP神经网络训练结果

式中,Tj是网络隐含层与输出层之间的权值,ωij是输入层与隐含层之间的权值,qj是隐含层的阈值,gk( k=1,2,3)是输出层的阈值。
4.3 神经网络泛化能力验证
神经网络的泛化能力是指经过训练后的神经网络对训练样本以外的任意输入数据,经神经网络预测能否得到准确输出的能力。用4组测试数据中工况1导轨最大变形量对本文构建的BP神经网络进行泛化能力的验证,立柱导轨最大变形量的预测输出和期望输出如图7所示,预测误差如表3所示。
BP神经网络模型的预测误差用下式计算:

式中,ypredicted为BP神经网络预测值,yactual为有限元计算值,e为BP神经网络预测误差。

图7 BP神经网络预测误差
由表3可知,本文建立的BP神经网络预测立柱导轨工况1下最大变形量的最大预测误差为1.07%,此外,工况2下导轨最大变形量最大预测误差为1.12%,首阶固有频率的最大预测误差为0.82%,立柱体积的最大预测误差为0.95%。表明本文建立的BP神经网络能较好地反映输入和输出数据之间的映射关系。
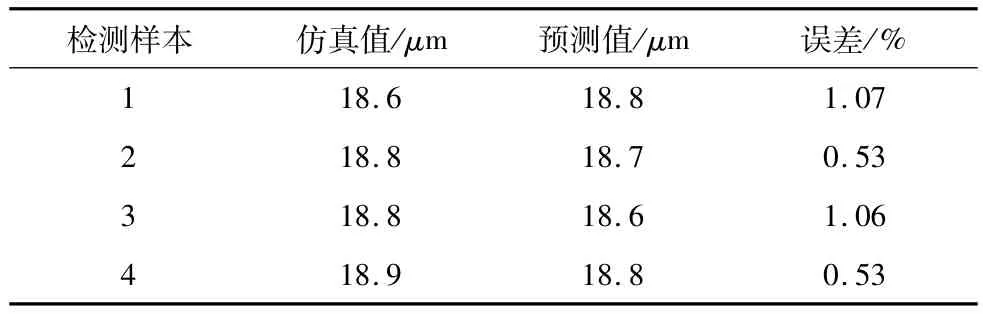
表3 有限元仿真值与BP神经网络预测值对比
5 优化算法及优化结果
遗传算法(GA,Genetic Algorithm)是Holland在60年代提出的,主要借助生物进化过程中“适者生存”的规律,模仿生物进化过程中的遗传繁殖机制,对优化问题解空间的个体进行编码(二进制或其他进制),然后对编码后的个体种群进行遗传操作(如:选择、交叉、变异等),通过迭代从新种群中寻找含有最优解或较优解的组合。遗传算法具有简单通用、鲁棒性强和适用于并行处理等显著特点[10],其在机械结构优化方面得到了广泛应用。
日本Doshisha大学的M.Kaneko等人为了解决传统遗传算法容易陷入早熟这一缺陷,提出了多岛遗传算法(MIGA,Multi-Island Genetic Algorithm)。多岛遗传算法将传统遗传算法中的单一种群分成多个子种群,子种群之间存在定期迁徙。多岛遗传算法的迁徙保持了解的多样性,可抑制早熟现象的发生[11],具有比传统遗传算法更优良的全局求解能力和计算效率。
文中立柱结构的最优尺寸是筋板厚度的组合问题,因此,优化算法必须是全局探索方法,鉴于多岛遗传算法的上述特点。本文选择多岛遗传算法作为优化算法。岛屿个数为2,每个岛屿中个体数目为50,进化代数为12,迁移率为0.5,迁移间隔为2,交叉概率为0.9,变异概率为0.01。
经过多岛遗传算法对本文建立的BP神经网络模型进行优化迭代1200次之后得到筋板厚度增量值的最优解。优化结果如表4所示,将优化后得到立柱进行有限元分析,得到立柱优化前后的导轨最大变形量、首阶固有频率和立柱体积如表5所示,可知优化后立柱导轨最大变形量和首阶固有频率变化很小,优化前后立柱前十阶固有频率最大变化为0.81%(限于篇幅,没有列出对比表),立柱体积减少了2.4%,达到了机床轻量化设计的目标。
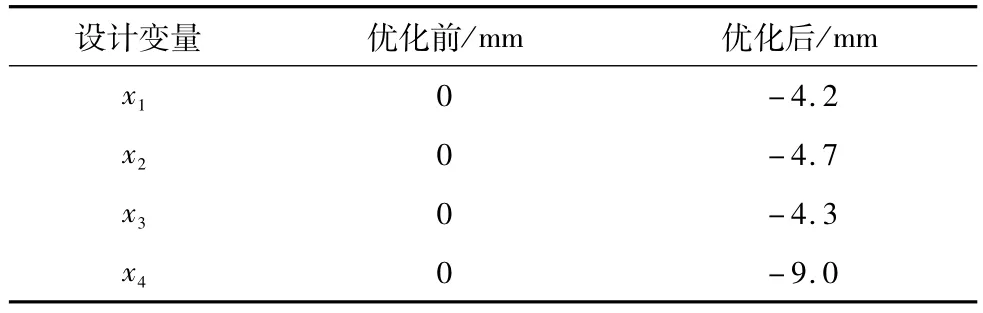
表4 设计变量优化结果

表5 优化前后评价参数对比
6 结论
本文以某型精密卧式加工中心立柱的优化设计为应用实例,提出了一种基于神经网络模型、网格变形和多岛遗传算法的复杂机械结构轻量化优化设计方法。对立柱初始结构进行了有限元分析,根据分析结果和优化设计要求,建立了立柱优化设计的数学模型。在优化设计过程中引入了网格变形技术,避免了每次优化迭代后立柱复杂三维模型的重构,提高了优化效率。为了缩短优化计算时间及更好的反映设计变量和立柱参数的映射关系,构建了BP神经网络模型近似替代立柱有限元模型。最后,为了求解设计变量的最优解,引入多岛遗传算法来求解文中建立的BP神经网络模型。该方法与目前机械结构优化普遍采用的基于多次数值分析的方案优选法和基于响应面模型优化方法相比,具有较高的优化计算效率和较好的计算精度。该方法也适合于其他结构复杂的机械零部件优化问题。
[1]苏渤,王永泉,朱祥,等.基于有限元分析的机床结构优化设计[J].精密制造与自动化,2011(4):30-33.
[2]郭春星,丁晓红,郭媛美,等.磨床床身结构优化设计[J].机械设计与研究,2009,25(5):104-107.
[3]李小彭,赵志杰,聂慧凡,等.某型数控车床床身的模态分析与结构优化[J].东北大学学报(自然科学版),2011,32(7):988-991.
[4]于海莲,王永泉,陈花玲,等.响应面模型与多目标遗传算法相结合的机床立柱参数优化[J].西安交通大学学报,2012,46(11):80-85.
[5]Auweraer H Van der,Langenhove TV,Brug-hmans M,etal. Application of Mesh Morphing Technology in the Concept Phase of Vehicle De-velopment[J].International Journal of Vehicle D-esign,2007,43:281-305.
[6]KO C,PARK J,PARK,K,etal.Morphing technique application for the automotive comp-onent analysis[R].SAE,2007 -01-3936,2007.
[7]周品.MATLAB神经网络设计与应用[M].北京:清华大学出版社,2013.
[8]赖宇阳.isight参数优化理论与实例详解[M].北京:北京航空航天大学出版社,2012.
[9]郑彬,殷国富,黄辉,等.重载大跨距横梁弯曲变形分析与补偿[J].振动、测试与诊断,2014,34(2):274-279.
[10]王小平,曹立明.遗传算法-理论应用与软件实现[M].西安:西安交通大学出版社,2003.
[11]牟淑志,杜春江,牟福元,等.基于多岛遗传算法的连续体结构拓扑优化[J].机械科学与技术,2009,28(10):1316-1320.
(编辑 赵蓉)
Optim ization Design Research of M achine Tool Column Based on Neural Network and M esh M orphing
WANG Liang,YIN Guo-fu,TAN Feng,DONG Guan-hua
(School of Manufacturing Science and Engineering,Sichuan University,Chengdu 610065,China)
Focusing on inefficiency and inherent lim itations in the traditional optim ization methods for complex mechanical structures and the purpose of lightweight design formachine tool,an optimization approach based on BP neural networkmodelandmeshmorphing technology(MMT)is proposed to dealw ith the optimal design problem for complex mechanical structures.The finite element analysis has carried on a certain type of precision machining center column and the optim ization mathematical model of column is established.Introducing MMT,a softwaremodule based on VB was developed to establish the parameterized finite elementmodel of column.An optimal Latin-hypercube was employed to sample the design space,and the BP neural networkmodel is established.The generalization ability of BP neural networkmodelwas tested,then,multi-island genetic algorithm(M IGA)was adopted to execute the optimization procedure,where them inimum volume of the column was regarded as object function,and themaximum deformation of linear guideways and the firstorder natural frequency were regarded as constraint conditions.The result shows that the total volume of column decreased by 2.4%under the prem ise of the maximum deformation of linear guideways and the first order natural frequency basically remain unchanged.The requirement of lightweight optim ization design formachine tool wasmet.
machine tool column;neural network;mesh morphing;multi-island genetic algorithm
TH122;TG65
A
1001-2265(2015)08-0005-05 DOI:10.13462/j.cnki.mmtamt.2015.08.002
2014-11-06;
2014-12-16
国家科技重大专项"高档数控机床与基础制造装备"课题(2013ZX04005-012)
王亮(1991-),男,四川巴中人,四川大学硕士研究生,研究方向为机械机构优化,(E-mail)543067792@qq.com;通讯作者:殷国富(1956-),男,成都人,四川大学教授,博士研究生导师,研究方向为制造自动化、智能设计技术、CAD/CAM/CIMS,(E-mail)gfyin@ scu.edu.cn。

