基于非支配遗传算法的自动化仓库动态货位优化*
印 美,洪荣晶,刘 林
(1.南京工业大学机械与动力工程学院,南京 211816;2.江苏省工业装备数字制造及控制技术重点实验室,南京 210009)
基于非支配遗传算法的自动化仓库动态货位优化*
印 美1,洪荣晶1,刘 林2
(1.南京工业大学机械与动力工程学院,南京 211816;2.江苏省工业装备数字制造及控制技术重点实验室,南京 210009)
针对存有随机数量货物的机床零部件自动化立体仓库(AS/RS)中存在的货位规划难题,提出了一种基于动态的仓储模式与Pareto遗传算法的AS/RS货位优化方法。该方法以能耗最低和效率最高为基本原则规划库区和优化分配货架,完成货位编号和货品编号;以堆垛机行驶时间和货架稳定性为优化目标,建立货位多目标优化的数学模型;采用第二代非支配排序遗传算法得到动态货位优化的Pareto最优解。仿真实例计算结果表明,该方法使货物的出入库能量消耗、出入库效率以及货架的稳定性等指标得到较大改善。
自动化立体仓库;货位动态分配;多目标优化;遗传算法
0 引言
自动化立体仓库(AS/RS,Automated Storage&Retrieval System)是指人工不直接进行处理的自动存储和取出货物的系统,它具有占地面积少、货位处理速度快、准确率高、降低库存积压等优点[1],对现代物流系统的作业效率和系统性能具有重要影响,在机床零部件的自动化管理系统中得到了广泛应用。
货位分配是影响自动化立体仓库作业效率和系统性能的重要因素,为了进一步提升自动化立体仓库性能,相关学者在自动化立体仓库货位分配优化方面进行了大量研究。罗键等[2]根据出入库点到货位小车的时间进行货位分区并进行了货位优化。杨鹏等[3]针对多载具自动化存取系统的货位分配优化问题进行了研究。MoonG等[4]研究了存储量变化时分类随机存储策略和货物再次分类策略对存储效率的影响,根据存储量变化的大小选择相应的货物存储策略。Ediz等[5]以货位分配、货位检索和货位存储保持最小化为目的建立数学模型,并基于最优订货策略采用遗传退火算法进行求解。
上述研究是在仓库空仓情况下的静态货位优化,通常情况下仓库存储着一定量的货物,同时存在出入库,需要随时给入库货物分配货位。此外,考虑到节能环保,本文将降低能耗对存储成本的影响作为优化目标之一。因此,综合考虑货位优化过程中能耗的影响、仓库的运行效率和货架的稳定性,建立多目标约束的优化模型,提出了一种基于第二代非支配排序遗传算法的动态货位优化分配方法,为出入库货物选择最佳货位。
1 自动化立体仓库货位问题描述
以某机电企业的立体仓库为例,每一巷道有左右两排货架。假设立体仓库每一列货位数量一致,货格大小相同,有n排p列q层,其货位的长度、高度分别为l、h,并将最接近入库台的一排记为第一排,最接近巷道口的一列记为第1列,最底下一层记为第1层,位于第x排y列z层的货位记为(x,y,z)(x=1,2,…,n;y=1,2,…,p;z=1,2,…,q)。针对上述仓库布局模式,下面采用分类随机存储策略结合货架受力均匀和稳定性原则、效率原则、分散存放原则进行自动化仓库的动态货位分配,具体分配策略内容如下:
(1)货位编号。为了形成货位的优先级顺序,需要对仓库货位的单位能耗进行排序,文献[6]中给出了一种货位单位能耗因子d(h,L)
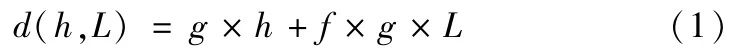
式中,g为重力加速度/m·s-2;h为货格的高度/m;L为货物所在货位到出入库台的水平距离/m;f为轨道与输送小车的摩擦系数。
根据公式(1),按d(h,L)由小到大的原则对仓库的货位进行排序并编号。货位编号的大小对应于货物存入该货位时所消耗能量的大小,当立体仓库的构造和布局确定时,可以得到相应的货位单位质量的能耗值,排序后单排货位编号如图1所示。
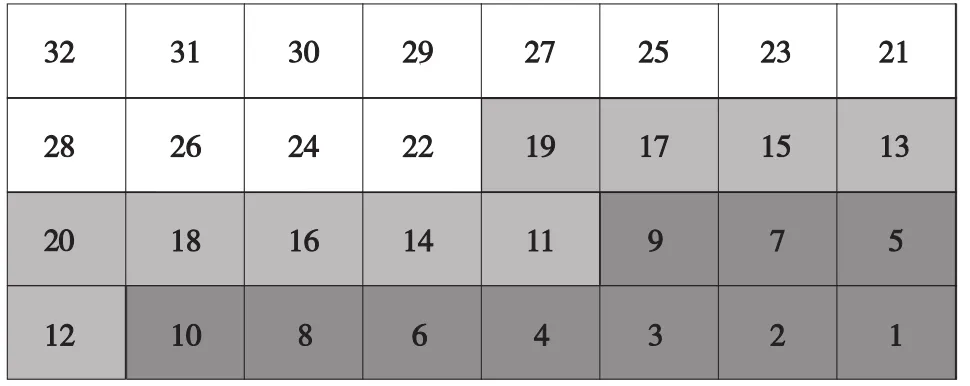
图1 单排货位编号
(2)货位联合编号。为了满足相同货品的分散存放和堆垛机运行的平衡,综合各巷道货架货位进行统一编号。将每排货架对应货位从左到右进行顺序编号,形成穿梭于各巷道之间的货位链,如图2所示是联合编号完成后货位排序。
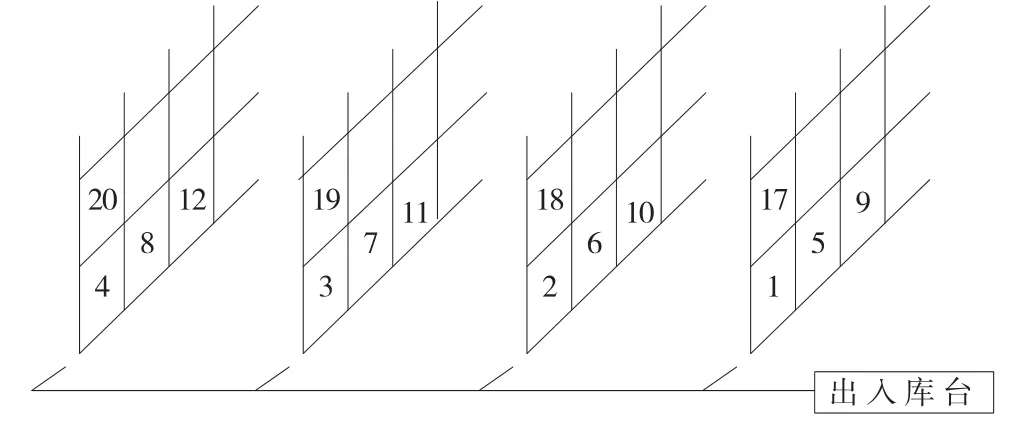
图2 联合编号示意图
(3)货品编号。为了使每个货品与合理的货位形成一一映射关系,依据货位-货品耦合原理[7],需要对货品的立方体索引号值(Cube-per-Order,COI)进行计算。由Heskett[8]给出的立方体索引号规则,并考虑到能耗的影响,将货品的COI值计算公式修改为:

式中,Ik表示某种货物k的COI值;Ck表示货物k存储总量所需的库存容量;fk表示货物k的出库频率;mk表示货物k的质量。
货品链的形成根据公式(2),由货品的COI值从小到大对货品进行排序,其顺序反映了货品的出入库频率和质量,然后将COI值低的货物与货位编号小的货位相对应,即将出入库频率高且质量大的货物放置在距离出入口近并且单位能耗低的货位上,这样既能提高出入库的效率又能降低仓库的运行成本。
2 货位优化多目标数学模型
根据货架稳定性原则和效率原则,以仓库运行能耗最低、出入库时间最小化和重心最稳作为优化目标,以仓库的实际运行状况为约束条件,建立货位优化的多目标数学模型。
2.1 货位区优化
设有s种货品,货位分区的目的是让货品的COI值Ik(k=1,2,…,s)较小的货品放置在单位能耗低的货位上,即使Ik与货位编号D的乘积Q最小,数学描述为:
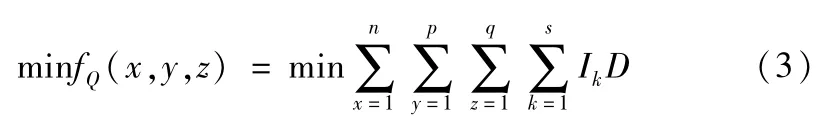
2.2 出入库时间分析
假设堆垛机在X方向、Y方向和Z方向均以匀速运动的,速度分别为vx、vy、vz,不考虑制动、启动堆垛机的耗时及伸入货格进行操作的时间,则出入库效率优化的数学描述为:
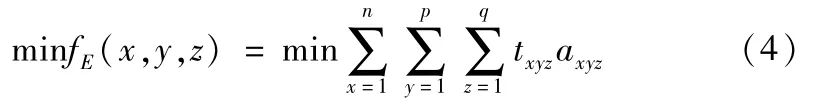
式中,txyz=(x+(x/2))d/vx+max(l×y/vy,h×(z-1)/vz),表示将货物送到分配的货位运行时间最小。axyz=0或1,为0时表示(x,y,z)货格没有货物,为1时表示(x,y,z)货格有货物。
2.3 货架稳定性分析
为了达到货架稳定目标,即重心最稳,将货物在货架上的分布视作质点系,其数学描述为:
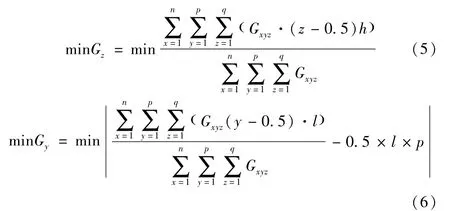
式中,Gz、Gy和Gxyz分别表示货架的垂直重心、水平重心和货架(x,y,z)货位处的货物重量,式(5)为了使货架的垂直重心接近货架的底层,使货架稳定;式(6)是为了使货架的水平重心接近货架水平方向的中心轴线。
因此,货架稳定性目标的数学描述为:
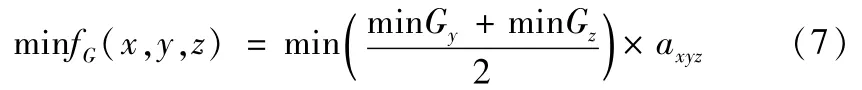
由于货架水平稳定性和垂直稳定性同样重要,货架任何一边不稳定都会造成严重后果,所以在水平和垂直方向上设置相同的系数,均为0.5。
2.4 货位优化数学模型
综上所述,货位优化的多目标数学模型可以描述为:

货架一共有n排p列q层,x、y、z均为正整数,分别表示货架的排、列、层,且1<x<n,1<y<p,1<z<q。
3 基于遗传算法的货位优化设计
由上述分析,货位动态分配优化模型是一个多目标优化问题,对于多目标优化问题,各个目标是相互冲突的,求解的关键是获得由Pareto最优解组成的集合,用遗传算法求解多目标问题的方法主要有SPEA2、NPGA2、SPGA、NSGA、NSGA-Ⅱ等,而第二代非支配排序遗传算法(NSGA-Ⅱ)较其他算法具良好的稳定性、收敛性以及所求得的Pareto最优解集分布均匀[9-10],本文采用该算法对货位动态分配的多目标问题进行优化,并且在个体生成时进行约束处理,使其满足约束条件,从而保证每个个体都是可行解。
基于NSGA-Ⅱ算法求解货位分配优化模型的步骤:
(1)获取当前的库存状态(包括货品与货位的信息);
(2)输入当前的任务信息(包括出入库、货品的任务数等);
(3)初始化并编码。设置最大迭代次数Kmax、种群数目pop、交叉概率pc、变异概率pm。采用实数编码,初始化群体,并计算个体适应度值;
(4)将群体个体进行非支配分层,设置虚拟适应度,计算个体拥挤度算子,修改虚拟适应度,按照轮赛制选择算子,进行选择,形成新种群;
(5)执行交叉、变异操作,在此对产生的个体进行约束处理,避免非法产生非法个体;
(6)精英保留策略,将父代种群Pt与子代种群Qt合并为临时种群Rt,进行非支配分层,并计算每个个体局部拥挤距离,依据轮赛制选取pop个个体,形成新的父代种群;
(7)在此基础上进行选择、交叉、变异,形成新的子代种群。如果迭代次数大于最大次数Kmax,则迭代终止;
(8)得到优化后的货位坐标,进行模拟仿真验证,根据优化结果,对货位重新排序。
如图3所示,为求解货位分配优化的算法流程图。
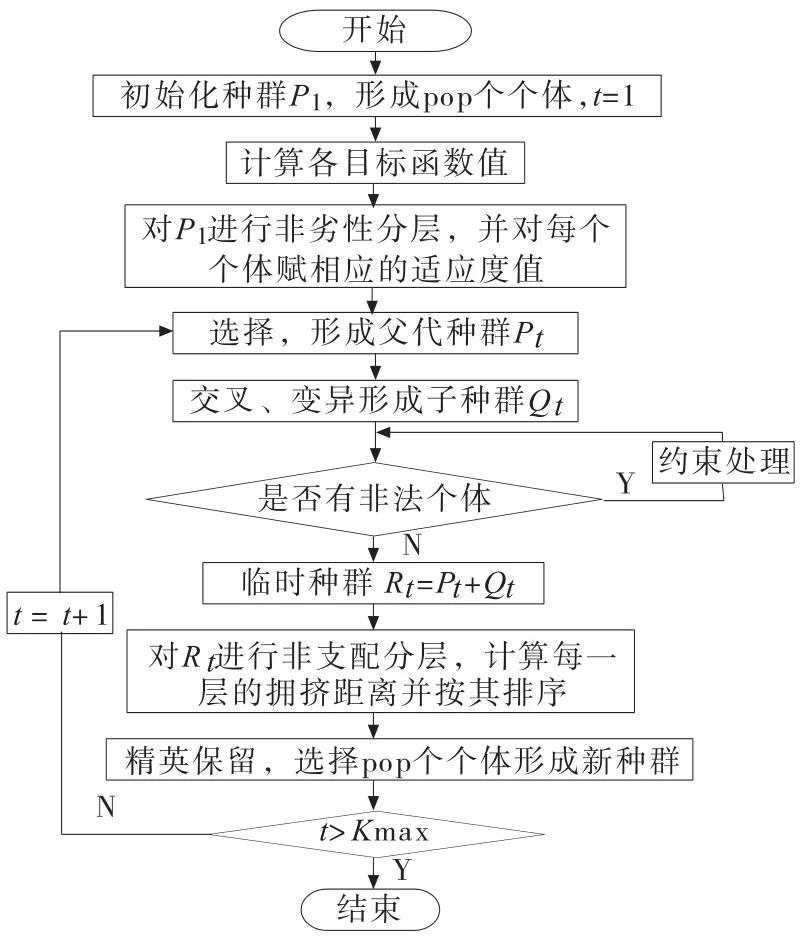
图3 求解货位分配优化的算法流程图
4 应用实例
4.1 基本参数
某自动化立体仓库有4排,每排8列4层,货位的长度d=120cm,宽度l=120cm,货位的高度h=80cm,堆垛机的水平运行速度vx=1 m/s、vy=1 m/s,垂直运行速度vz=0.5 m/s。货物的参数如表1所示,第一列表示货物1的质量是20 kg,作业概率为30%,需要的货位个数是50个,分配在B区,以此类推,已知每类货物的质量,作业概率和所需要的货位数。
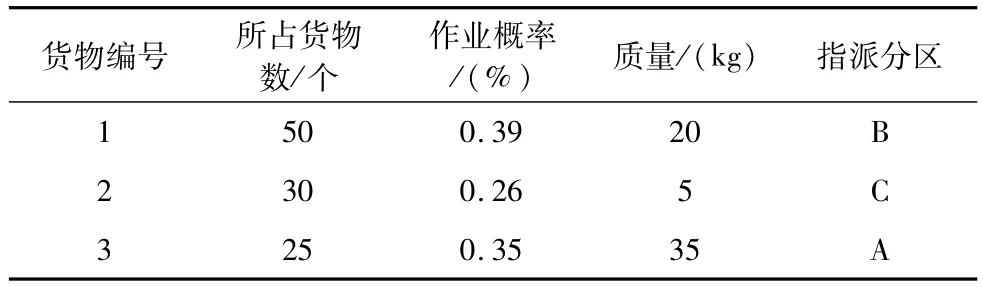
表1 仓库货物基本参数
根据货位区分配结果,质量越大、作业效率越大的货物放在距离出入口越近货位区的可能性越大,即1类货物放在B区,2类货物放在C区,3类货物放在A区,仓库货物基本参数见表1。
仿真计算实例中,假设共有2个货物需要入库,其中1类货物、2类货物各1个。共有2个货物要出库,为3类货物。货位进行优化前,仓库的布局情况见图6a,当前库存为15个,分别是1类货物5个,2类货物4个,3类货物6个。
4.2 仿真结果
仿真结果分析:按照上述NSGA-Ⅱ对多目标优化问题的求解方法,设置算法种群规模为200,交叉概率为0.9,变异概率为0.1,进化最大代数为100。编程并对其进行数值模拟计算,运行结果如图4所示。
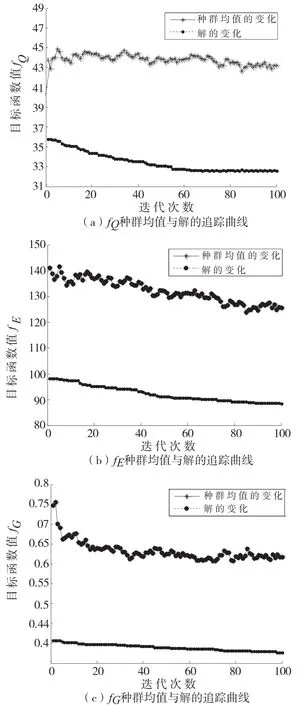
图4 种群均值和解的追踪曲线
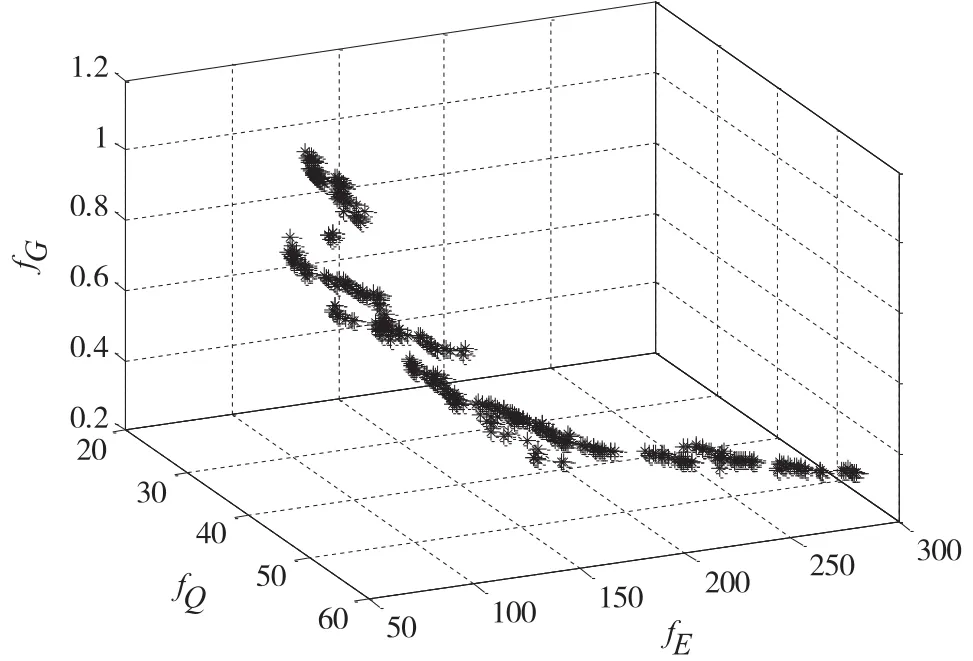
图5 目标函数解的分布
图4 为种群均值和解追踪曲线,图5为目标函数解的分布图,由图4、图5可见,种群进化到70代时已基本收敛,当种群进化到100代时,Pareto最优解具有良好的多样性,NSGA-Ⅱ的搜索结果是令人满意的。
选取其中的三组具有代表性的Pareto最优解作为货位优化方案,对比货位优化前后的三个目标函数值,如表2所示,较之优化前,其货物存储能耗fQ、出入库时间fE和货架重心fG平均值分别降低了39.20%、61.84%和47.62%,在Pareto最优解集中,三个目标之间是竞争关系,当其中一个减小时,必然会导致其他两个目标值相应增大。

表2 优化前后三个目标函数值对比
4.3 模型验证
如图6所示,是采用数值模拟计算出的优化前后货位分配状态的三维示意图。对比优化前后货位分配状态表明,优化前的货位布局不合理,仓库的综合性能比较差,货位优化后,货位分配布局合理,满足出入库效率和货架稳定性要求且能耗最低。同类货物的货区有相应的空缺货位,是因为再次入库时可以直接存放货物到对应货位区,无需再进行倒库操作。再次出库时,仅需取出相应货位区的货物即可。此外,由仿真结果知,并非所有Ik较小的货物都放在编号较小的货位上,这是因为货位优化是一个多目标的问题,多个目标相互矛盾,在求解的过程中,为了满足多目标最优,部分优化目标有妥协的趋势。

图6 优化前后货位分配状态对比
5 结论
本文提出了一种基于NSGA-Ⅱ算法的自动化立体仓库动态货位优化方法,该方法在综合考虑堆垛机运行时间最短和货架重心最稳的前提下,兼顾了仓库运行能耗最低为优化目标,通过对生成个体进行了约束处理有效地避免非法个体的产生,较好地解决了货位优化多目标之间相互冲突的妥协求解问题。仿真实例表明,所建立的模型能较好的兼顾货位分配时的能耗、效率和货架稳定性要求,得到的Pareto最优解为出入库货物分配了合理货位,该优化算法可满足工程应用实际需求。
[1]中国仓储协会仓储设施与技术应用委员会.自动化立体仓库应用及发展展望[J].物流技术与应用,2013(4):106-108.
[2]罗键,钟寿桂,吴长庆.基于离散粒子群算法的A VS/R S货位优化[J].厦门大学学报,2009,48(2):212-215.
[3]杨朋,缪立新,戚铭尧.多载具自动化存取系统货位分配优化[J].计算机集成制造系统,2011,17(5):1050-1055.
[4]Moon G,Kim GP.Effects of relocation to AS/RS storage location policy with production quantity varition[J].Computer and Industrial Engineering,2001,l(4):1-13.
[5]Atmaca Ediz,Ozturk Ayla.Defining order picking policy:A storage assignment model and a simulated annealing solution in AS/RS systems[J].Applied Mathematical Modeling,2012,37(7):5069-5079.
[6]银光球,何福英,盛冬发.自动化立体仓库中库位优化模型研究[J].福建工程学院学报,2006,4(3):347-350.
[7]张跷萍,刘文煌.CIMS物流系统的关键技术[J].计算机集成制造系统,1997,3(1):22-24.
[8]Heskett J L.Cube-per-order index-a key to warehouse stock location[J].Transportation and Distribution Management,1963,3(4):27-31.
[9]Zitzler E,Thiele L.Multi-objective evolutionary algorithms:a comparative case study and the strength Pareto approach[J].Evolutionary Computation,IEEE Transactions on,1999,3(4):257-271.
[10]Kalyanmoy Deb,Amrit Pratap,Sameer Agarwa.A fast and elitist multiobjective genetic algorithm:NSGA-II[J].IEEE Transaction on Evolutionary Computation,2002,6(2):182-197.
(编辑 李秀敏)
Optimization for Dynamic Location Assignment of AS/RS Based on Non-dominated Sorting Genetic Algorithm
YIN Mei1,HONG Rong-jing1,LIU Lin2
(1.School of Mechanical and Power Engineering,Nanjing Tech University,Nanjing 211816,China;2.Jiangsu Key Laboratory of Digital Manufacturing for Industrial Equipment and Control Technology,Nanjing210009,China)
To solve the slotting optimization of AS/RS,in which random spaces were occupied,an optimization method based on the dynamic storage strategy and non-dominated sorting genetic algorithm II(NSGA-II)was proposed.In this method,low energy consumption and high efficiency were taken into consideration for the section assignment and the locations and goods were numbered.Then,the optimization model was established for location assignment by defining the optimal objectives as the travel time of Storage/Retrieval machines and the stability of the whole warehouse.Finally,the optimal Pareto solution of dynamic location assignment was obtained using the NSGA-II.A numerical example demonstrated the feasibility of the proposed method,which not only reduced the energy and time consumption of storage and retrieval cycle,but also improved the stability of the whole warehouse.
automated storage/retrieval system;dynamic location assignment;multi-objectives optimization;non-dominated sorting genetic algorithm
TH246;TG65
A
1001-2265(2015)03-0031-04 DOI:10.13462/j.cnki.mmtamt.2015.03.009
2014-05-30;
2014-06-03
国家自然科学基金资助项目(51375222)
印美(1989—),女,江苏泰兴人,南京工业大学硕士研究生,研究方向为机械制造及其自动化,(E-mail)ymclara@sina.com。

