基于极值法与统计公差法的不同尺寸公差分配方法的研究*

基于极值法与统计公差法的不同尺寸公差分配方法的研究*

龚 鑫，黄美发，孙永厚，肖萌萌，吴 芬
（桂林电子科技大学机电工程学院，广西桂林 541004）

对装配体的尺寸公差分配是产品公差设计中的一项重要环节。公差的大小决定着产品的制造成本，对装配尺寸公差进行合理分配具有重要意义。然而在两种不同的公差分析方法下其各种公差分配也有所不同。文章介绍了目前装配尺寸公差分配的主要方法，有等公差法、等精度法和最优化分配法等。结合齿轮轴工程实例，分别运用极值法和统计公差法对各种尺寸公差分配方法进行分析研究。其结果表明，在实际运用中利用装配功能公差链统计公差法约束条件并考虑加工方法的经济性公差约束条件对装配尺寸公差进行分配为最优化分析方案。并将其集成到计算机公差设计系统中。

装配尺寸公差分配方法；极值法与统计公差法；计算机公差设计系统

0 引言

随着机械制造精度及产品功能要求的提高，产品设计阶段的装配尺寸公差分配引起了广泛关注，它不仅影响机械产品的质量，而且对产品的制造成本起着决定性作用。因此，在保证产品性能要求的必要前提之下，合理的公差分配是降低生产成本和满足产品性能的重要因素。所以，按照一定的方法和约束条件，对装配尺寸公差进行合理分配具有重要意义。

在公差设计集成系统中的公差分配模块是将封闭环的公差信息以及已知组成环的公差信息作为输入，通过程序的运算，输出待求组成环的公差信息［1］。目前，国内、外学者在公差设计集成系统中的装配公差分配模块领域进行了诸多研究，在文献［2-8］中，许多学者对处理他们一般特征的公差分析模型进行了对比发现，装配尺寸链的功能要求约束可以从极值法和统计公差法中选择一种，这两种计算方法有着各自的优势和不足，然而在实际应用中不同企业采用的方法都有所不同。但是这些研究把注意力仅仅放在考虑模型的一般特性，存在较少的论文来对比这个不同的分析方法基于一个实例的研究来强调它们的优缺点，因此，对企业来说，在满足特定的公差要求下没有通过综合对比来选择一个最优方案。本文结合目前公差分配的基本方法，针对两种不同公差分析方法（极值法和统计公差法）及相应的约束条件，提供引导在特定的目的下来选择一个最优分析方案。并将它们集成到计算机公差设计系统中［9-10］。

1 装配公差优化分配的数学模型

在公差分配中，所有组成环中包括已知组成环和待定组成环，

其中n、ns、nt分别为总组成环数、已知组成环数以及待定组成环数。运用极值法以及统计公差法的计算基本公式分别为：

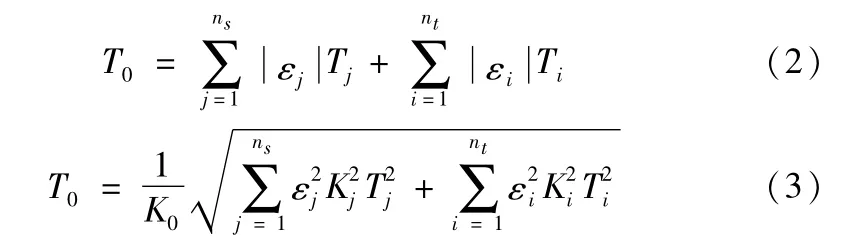
式中，i=1，2，...nt，j=1，2，...ns；

T0、Ti分别表示封闭环公差以及组成环公差；

εi、εj表示组成环误差传递系数；

K0、Ki分别表示封闭环的相对分布系数以及组成环的相对分布系数。其中，正态分布、三角分布、均匀分布、瑞利分布的相对分布系数K取值分别为1、1.22、1.73、1.14。

1.1 等公差法

等公差法是对所有的待定组成环分配相等公差值的方法，该方法是一种公差平均分配法。

规定待定组成环所取的相等的公差为平均公差，用Tav表示。Ti=Tav（i=1，2，...nt）代入式（2）、（3）中分别利用极值法以及统计公差法计算待定组成环的公差值，得到基本公式如下：

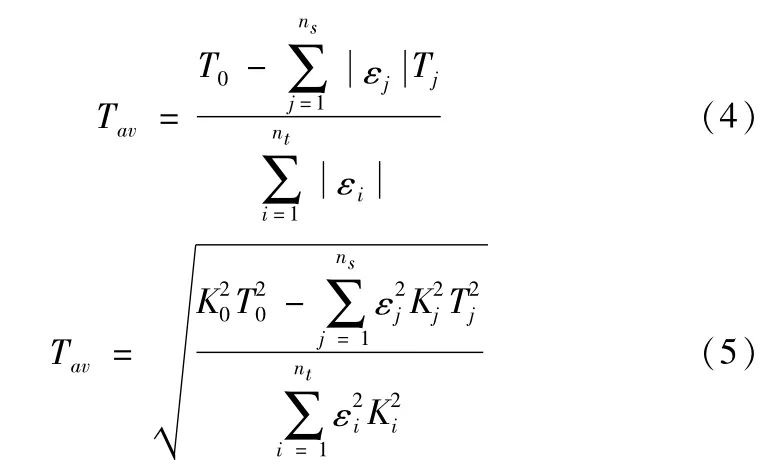
1.2 等精度法

等精度法是所有的待定组成环取得相同公差等级的方法。该方法先求出公差等级的系数，再确定各组成环的公差并作适当的调整。

由表1可知：机械行业常用的公差等级IT5～IT18的标准公差计算公式为：

式中α为公差等级的系数，I为公差因子。公差因子的取值由基本尺寸D决定，在常用尺寸段内：

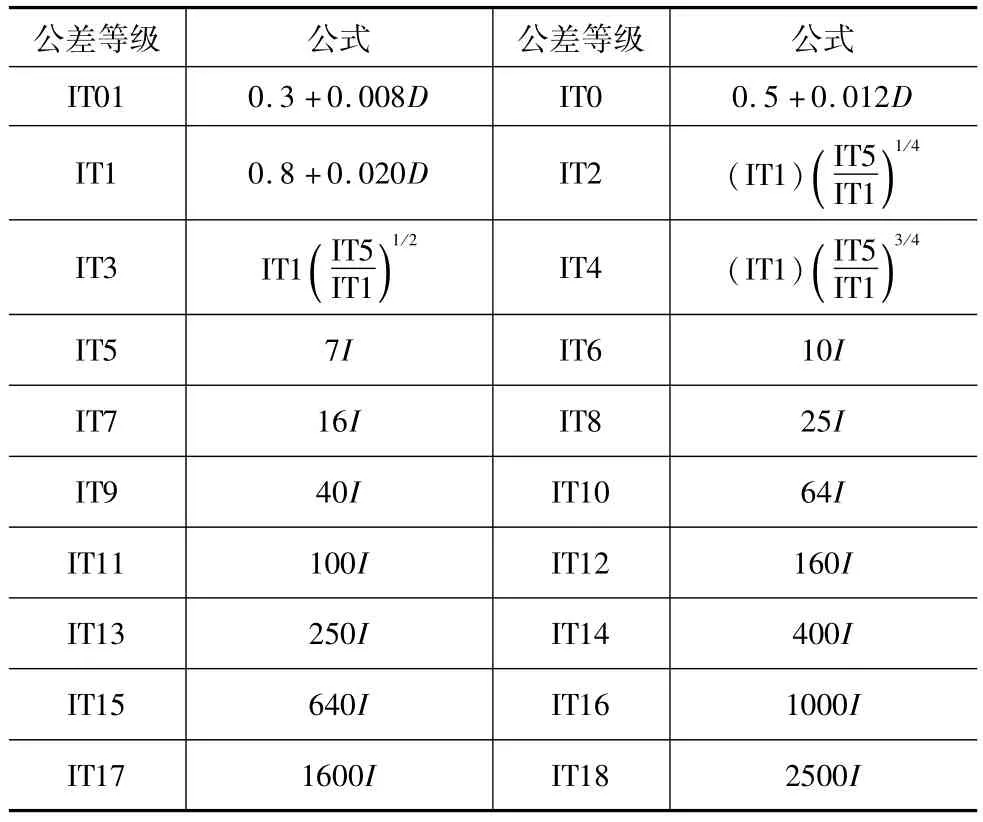
表1 基本尺寸不大于500mm的标准公差数值计算公式

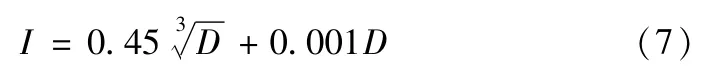
式（7）中的基本尺寸D为每一尺寸段中首、尾两个尺寸的几何平均值，即：

将式（7）代入式（2）、（3）中分别利用极值法以及统计公差法计算待定组成环的公差等级的系数，得到基本公式如下：

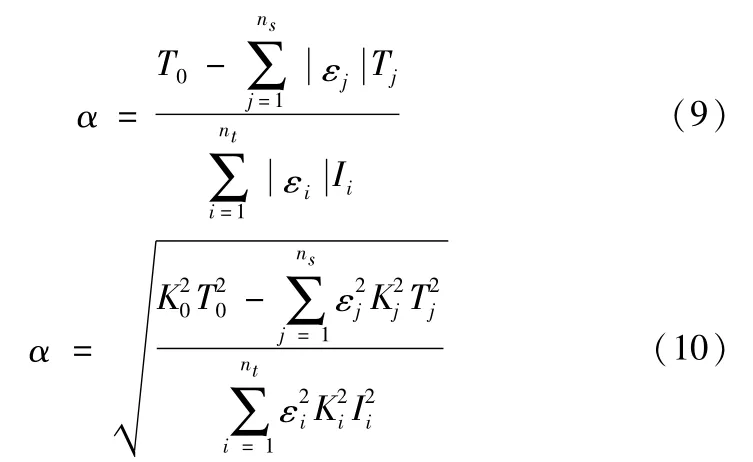
1.3 最优化分配法

在装配尺寸链中，各组成环的加工成本累加总和最小即是公差优化分配的目标［11］，故目标函数：

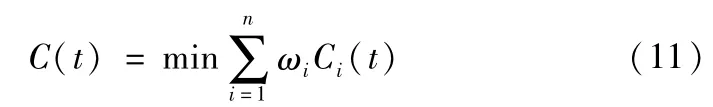
式中ωi为第i个组成环加工成本的权重系数，它与在同一加工要求下采用不同加工设备与加工方法造成的成本差异相关；Ci（t）为第i道工序加工方法时的成本公差函数。依据对应工艺卡片，毛坯经过加工工序得到该设计尺寸，一般来说，每一种工序的选择方案及各种加工方法对应着相应的经济精度，对于粗加工ω=1，精加工ω=1.3，较高功能要求的加工ω=2。

1.3.1 约束条件

在公差优化分配领域中，有多种约束条件如装配功能公差链约束、加工合格率概率约束以及加工方法的经济性公差约束等，在实际中主要采用简单且计算方便的装配功能公差链约束和加工方法的经济性公差约束。

装配功能公差链约束主要保证当封闭环公差确定后，封闭环公差应该不小于各组成环公差的累加，以确保装配的精确性和准确性。装配功能公差链极值法约束条件以及装配功能公差链统计公差法约束条件的数学表达式分别如下：

加工方法的经济性公差约束条件要求各组成环的公差不能超过实际的加工功能，其数学表达式如下所示：

式中：Timin为装配尺寸公差链中第i个组成环的最小加工能力公差；

Timax为装配尺寸公差链中第i个组成环的最大加工能力公差。

2 实例分析

图1所示是一个减速器的齿轮轴装配图。该装配体中，由机体、左端盖、左轴承、轴、齿轮、支撑环、右轴承、调整环和右端盖组成了一个水平方向的尺寸链，具体公式如下：

式中，L1、L2、L3、L4、L5、L6、L7、L8和L9分别表示机体、左端盖、左轴承、轴、齿轮、支撑环、右轴承、调整环和右端盖在尺寸链方向的相应尺寸。其中，L8（调整环）是封闭环。

图1 减速器的齿轮轴装配图

由于左轴承和右轴承是标准件，其公差值t3和t7都为固定值0.12mm。且按照装配的要求，封闭环的公差值t8应小于0.5mm。

2.1 等公差法分析

在实际生产中各组成环、封闭环一般取正态分布，则对应的相对分布系数通常均取K=1，对应的传递系数均取ε=1。代入公式（4）、（5）中，分别得出：

2.2 等精度法分析

根据尺寸分段，实例具体尺寸链组成环所属尺寸段，代入公式（8）中，再将（8）中所得结果代入公式（7）中，计算得出各组成环的公差因子。根据某企业的生产数据：L1=200、L2=8、L3=30、L4=15、L5= 80、L6=25、L7=30、L8=8、L9=4分别计算得出：I1=2.8959，I2=0.898，I4=1.0827，I5=1.856，I6= 1.3074，I8=0.898，I9=0.733。

把所得公差因子代入式（9）、（10）中，分别得出：α≤26.89，查表1取α=25则属于IT8；α≤114.53，查表1取α=100则属于IT11。

2.3 优化分配法分析

装配公差优化分配将经济性作为公差分配优劣的主要评价指标，在保证装配功能要求的情况下，以最低的制造成本设计出尽可能大的零件公差。可见，装配公差优化分配的数学模型是由目标函数和约束条件组成。

由于左轴承和右轴承的成本为常数，因此利用指数和倒指数积复合函数以及线性和指数复合函数的组合构造的公差分配模型的目标函数如下：

在装配尺寸链中L8是封闭环。装配尺寸链的功能要求约束采用极值法即装配功能公差链极值法约束条件，具体公式如下：

将具体参数代入式（17）得到最后的装配功能约束如下：

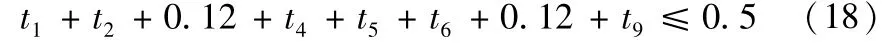
各组成环公差的加工能力约束如下所示：

在Matlab软件遗传算法的工具栏中将适应度函数设为目标函数M文件的句柄，将变量个数设置为6，并分别输入各个变量的边界约束条件和非线性不等式约束条件。除此之外，在遗传算法工具栏中采用默认的种群数目20，交叉概率0.8以及变形概率0.2。利用遗传算法工具栏进行优化搜索的操作界面如图2所示。对于该实例进行优化后，得到的最小成本值为65.6108，且组成环t1、t2、t4、t5、t6、t9对应的公差值分别为 0.06mm、0.039mm、0.041mm、0.045mm、0.036mm、0.04mm，遗传算法搜索后的优化结果如图2所示。

图2 极值法下的参数设置及所得结果

同理，如果装配尺寸链的功能要求约束采用统计公差法即装配功能公差链统计公差法约束条件，具体公式如下：

对于该实例进行优化后，得到的最小成本值为43.4421，且组成环t1、t2、t4、t5、t6、t9对应的公差值分别为 0.1mm、0.074mm、0.062mm、0.087mm、0.062mm、0.074mm，遗传算法搜索后的优化结果如图3所示。

通过分别利用极值法与统计公差法对不同公差分配方法进行分析计算，结果如表2所示。

结果表明：装配功能公差链极值法约束条件会导致分配到各个组成环的公差值较小，造成加工成本增大，不适宜在大批量产品的公差分配中使用，常用于小批量高精度产品公差优化分配中。

图3 统计公差法下的参数设置及所得结果

表2 各分析结果统计

然而，等公差法容易形成大尺寸小公差、加工困难的问题，一般只用于精度要求不高的粗略估算。且等精度法只考虑了尺寸大小这一因素，若尺寸大小相同，则公差值就相同。

故在实际运用中主要联合利用装配功能公差链统计公差法约束条件以及加工方法的经济性公差约束条件作为整个公差最优化分配模型的约束条件来计算各分配公差。

同时，利用Matlab软件进行编程生成公差分配方法分析模块，通过输入相关数据实时对比，实现公差分配方法的最优选取，如图4所示。

图4 公差分配方法分析模块

3 结论

装配尺寸链的功能要求约束可以从极值法和统计公差法中选择一种。结合一个工程实例，通过在不同的公差分配方法下计算分别利用极值法和统计公差法的分配公差，得出在实际运用中主要联合利用装配功能公差链统计公差法约束条件以及加工方法的经济性公差约束条件作为整个公差最优化分配模型的约束条件来计算各分配公差。并以此为依［参考文献］

据，利用Matlab软件编程集成到计算机系统，实现公差分配方法的最优选取。

［1］王平，沈跷阳.公差分析中的统计公差方法综述［J］.工具技术，2008，42（10）：43-47.

［2］马玥.虚拟装配中公差分析技术研究［D］.北京：中国工程物理研究院出版社，2006.

［3］郑丞，金隼，来新民，等.基于非合作博弈的公差分配优化［J］.机械工程学报，2009，45（10）：159-165.

［4］匡兵，黄美发.基于粒子群算法的装配公差优化分配［J］.机械设计与制造，2009（2）：35-37.

［5］杨文龙.面向装配的公差设计系统研究［D］.哈尔滨：哈尔滨工业大学出版社，2011.

［6］G.Prabhaharan，P.Asokan，P.Ramesh，et al.Geneticalgorithm-based optimal tolerance allocation using a leastcost model［J］.Int.J.Advanced Manufacturing Technology，2004，24（9）：647-660.

［7］Gagandeep Singh，Gaurav Ameta，Joseph K Davidson，et al.Tolerance analysis and allocation for design of a self-aligning coupling assembly using tolerance-maps［J］.Journal of Mechanical Design，2013，135（3）：31-45.

［8］Loïc Andolfatto，François Thiébaut，Claire Lartigue，et al. Quality and cost-driven assembly technique selection and geometrical tolerance allocation for mechanical structure assembly［J］.Journal of Manufacturing Systems，2014，33（1）：103-115.

［9］石仁庆.基于CAD的公差分析与设计［D］.北京：北京化工大学出版社，2007.

［10］张根保.计算机辅助公差设计及其关键技术［A］.全国首届计算机辅助公差设计专题会议论文集［C］.杭州：浙江大学出版社，2000.

［11］方红芳，陈淼森，陈冰冰，等.CAPP中的工序公差设计及技术经济评价［J］.中国机械工程，2001，6（12）：657-660.

Study On Different Tolerance Allocation Method Under Deterministic and Statistical Tolerance Analysis

GONG Xin，HUANG Mei-fa，SUN Yong-hou，XIAO Meng-meng，WU Fen
（School of Mechanical and Electrical Engineering，Guilin University of Electronic Technology，Guilin Guangxi 541004，China）

The assembly tolerance allocation is an important link in tolerance design.The manufacturing cost of the product is determined by the size of tolerance，reasonable allocation is of great significance to the assembly tolerance.However，the assembly tolerance allocation is also different in different tolerance analysis method.This paper introduces the main methods of assembly tolerance allocation，including equal tolerance，equal precision method and the optimun allocation method，i.e.In combination with the project example，we analyze all tolerance allocation method using deterministic and statistical tolerance analysis.The results show that，in the actual application of the assembly tolerance chain using statistical tolerance method constraints and consider the economic tolerance constraints processing method distribute the assembly tolerance as optimization scheme.And integrated it into the computer tolerance design system.

the assembly tolerance allocation method；deterministic and statistical tolerance analysis；computer tolerance design system

TH391；TG506

A

1001-2265（2015）03-0005-04 DOI：10.13462/j.cnki.mmtamt.2015.03.002

2014-06-11；

2014-09-02

国家自然科学基金（51365009）；广西制造系统与先进制造技术重点实验室主任课题资助项目（13-051-09-009Z）

龚鑫（1990—），男，江西丰城人，桂林电子科技大学硕士研究生，研究领域为精密测量与精密仪器，（E-mail）421896525@qq.com。