基于证据理论的多传感器融合故障诊断方法*

权宏伟，李俊华，彭冬亮

（1.西京学院机电工程系，西安 710123；2.杭州电子科技大学信息与控制研究所，杭州 310018）

基于证据理论的多传感器融合故障诊断方法*

权宏伟1，李俊华1，彭冬亮2

（1.西京学院机电工程系，西安 710123；2.杭州电子科技大学信息与控制研究所，杭州 310018）

在多传感器故障诊断系统中，需要建立故障特征参数空间到故障类型空间的对应关系，同时还需要解决不同传感器对同一机器的诊断结果可能存在冲突的问题。基于证据理论的多传感器融合故障诊断方法可以较好的解决上面的问题。论文首先结合机械故障诊断系统讨论了D-S证据理论，然后给出两传感器融合诊断的具体实例，最后对比分析了单传感器诊断与融合诊断的仿真结果。实验表明，基于D-S证据理论的融合诊断方法可以有效的解决多传感器之间的证据冲突问题，并在一定程度上提高了故障诊断决策的准确性。

故障诊断；D-S证据理论；多传感器融合；信任度函数

0　引言

使用多传感器数据进行机械故障诊断通常涉及两个主要问题：一是如何从不同类型的传感器数据中提取机械故障的特征信息，并以一种统一的方式来描述它们，从而建立特性信息空间到故障空间的映射模型；二是采用什么样的机制来融合这些信息，以使得最后做出的机械发生故障的决策更加准确。

目前，针对多传感器融合的故障诊断问题，国内外已有很多学者展开了相关的研究［1-3］。其中的一个研究方向是基于贝叶斯理论构建机械故障诊断模型。它的基本思想是，假设故障模型中状态变量的先验概率和条件概率能够被事先确定，根据贝叶斯公式，可以得到故障状态变量的后验概率，从而决定机器的故障状态。文献［4］使用了一种贝叶斯融合策略来提升X光成像系统的动态范围。在该系统中，图像信息是在两种不同环境下分别由各传感器采集得到。然而，基于贝叶斯理论的故障诊断方法需要严格的假设条件和先验信息，在很多实际的应用环境中，这些假设通常很难满足。

近几年来，基于D-S证据理论的故障诊断方法开始受到国内外学者越来越广泛的关注，已有大量的文献从理论和应用的角度讨论了这一方法［5-8］。文献［9］给出了一种使用D-S证据理论融合多分类器信息的新技术，它的特点在于根据传感器信息自适应的训练数据以达到系统的均方误差最小。文献［10］详细讨论了贝叶斯与D-S方法之间的差异。结果显示，在多传感器数据融合过程中，与贝叶斯方法相比，D-S证据理论没有对先验信息的要求，从而能更加灵活的应用到实际的工程实践中。文献［11］提出了一种使用D-S证据理论来诊断感应电机机械故障的方法。在诊断过程中，首先通过电动机定子上的电流信号和振动信号提取机械的特征信息，然后通过融合两类特征信息提升诊断结果的准确度。

随着机械安全与可靠性要求的不断提高，如何准确有效的诊断机械故障已经成为机械工程领域备受重视的问题。同时，由于机器结构复杂度的不断提高，单个传感器很难满足机器状态监测的要求。这就要求同时使用多个同类或异类传感器来完成机器状态监测及故障诊断。这也是多传感器数据融合理论中，基于证据理论的故障诊断方法所面临的新的挑战。

本文首先结合机械故障诊断系统讨论了D-S证据理论，然后给出两传感器融合诊断的具体实例，最后对比分析了单传感器诊断与融合诊断的仿真结果。实验表明，基于D-S证据理论的融合诊断方法可以有效的解决多传感器之间的证据冲突问题，并在一定程度上提高了故障诊断决策的准确性。

1　D-S证据理论

D-S证据理论的思想最初是由Dempster在1967年提出的，之后Shafer在此基础上进行了扩充和发展，最后形成了D-S证据理论的基本框架。D-S证据理论的主要内容包括四个方面：辨识框架，基本概率赋值，信度函数和证据融合。假定Θ=｛θ1，θ2，…θn｝是一个非空集合，该集合中的元素具有互斥和可穷举的特性，每一个元素代表一种假设或者一类故障，整个集合包含了所有可能的假设或故障。集合Θ的所有子集组成一个集合，称为Θ的幂集，用2Θ表示。如Θ=｛a，b，c｝，则

在机械故障诊断系统中，空集Φ可以表示机器处于无故障状态。集合｛a，b｝表示机器存在故障a或者故障b。Θ也被称为系统的辨识框架。为了量化集合中元素的信任度，定义一个mass函数，称为基本概率赋值（BPA，basic probability assignment），它是集合2Θ中的任一元素与区间［0，1］上的某个实数之间的映射，即

且有：

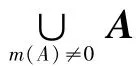
有了上面的定义，现在可以计算集合元素的信任度函数Bel（A）与似真度函数Pls（A）。尽管基本概率赋值函数表达了关于一个集合元素的信任程度，但不包括对它的子集的信任，因而，mass函数还仅是一个较为局部的变量。集合A的信任度函数Bel（A）与似真度函数Pls（A）定义为：

对于上面的集合2Θ，有

显然，Bel（A）与Pls（A）存在如下关系：

从而，在区间［0，1］上，可以得到一个由信任度函数与似真度函数构成的证据区间（EI，Evidence Interval），如图1所示，它可以较好的描述集合A的不确定性。

图1　集合不确定性的证据区间表示

在机械故障诊断系统中，为了能够更加准确的确定故障的类型，通常采用多个传感器对机械进行检测，因而必须考虑在同一时刻将来自多个传感器的信息融合起来的问题。在证据理论中，它被称为证据合并。假设A、B为辨识框架Θ的两个焦元，m1、m2为定义在框架Θ上的两个mass函数，根据Dempster正交化规则，有

式中，

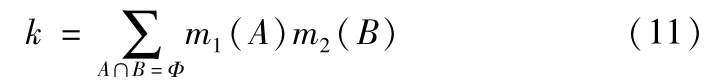
表示证据之间的冲突程度，k的值越大，说明证据之间的冲突程度越高。新得到的函数m（C）也是辨识框架Θ上的mass函数，它表示将两类数据源m1与m2合并后对当前集合内元素的信任程度。这一证据合并规则又可用下面的符号表示，即

且满足如下规则：

2　多传感器数据融合

假设当前某机器可能存在两种类型的故障，从而对应的故障诊断系统辨识框架可表示为Θ=｛x1，x2｝。式中，x1、x2分别表示机器发生第一类故障及第二类故障。显然，框架Θ的幂集应表示为2Θ=｛Φ，x1，x2，｛x1，x2｝｝，式中，Φ表示机器处于无故障状态，焦元｛x1，x2｝表示机器或者发生第1类故障或者发生第2类故障。在机械故障诊断的证据理论方法中，介于上面的假设，机器所有可能发生的故障必须彼此独立，并且在同一时刻最多只能发生一类故障。为了计算本例中幂集2Θ上的基本概率赋值（mass函数），首先建立如下故障原型的状态描述矩阵：

式中，Si（i=1，2，3，4）分别对应幂集2Θ中的四种状态：无故障，第1类故障，第2类故障，第1类或第2类故障。对于每一种状态，假设用m个特征参数来描述，即矩阵（14）中的sij（j=1，2，…，m）表示了第i种状态的第j个特征。通常情况下，从一个传感器的量测数据中可以提取一个或几个特征参数。如果用Yk表示第k个传感器的量测向量，则

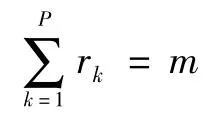
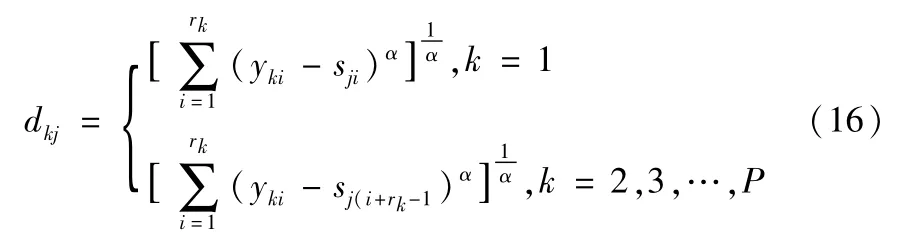
式中，mk（k=1，2，…，P）即为传感器k对应的mass函数。

3　仿真及结果分析

为了说明方便，这里假设同时使用两个传感器检测机器的两类故障。传感器1为振动传感器，测量信号的方差；传感器2为声传感器，测量信号的频率。两个传感器的采样周期均为1s，数据提取时间为200s。测量数据分别如图2、图3所示。

图2　传感器1的测量信号

图3　传感器2的测量信号

将上面的量测数据分别代入式（14）、式（15），计算得到两个传感器的mass函数。然后根据mass函数得到两传感器各自对机器故障的诊断结果如图4、图5所示。

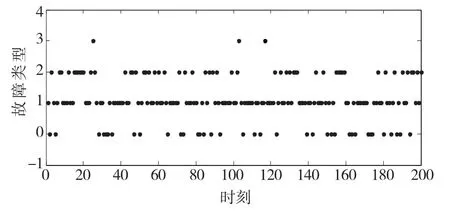
图4　传感器1的诊断结果

图5　传感器2的诊断结果

图中，纵坐标0，1，2，3分别表示机器的四种状态：即无故障，第1类故障，第2类故障，第1类或第2类故障。为了比较证据理论方法的融合诊断结果，我们同样使用上面的传感器数据，在得到两个传感器的mass函数之后，代入公式（10）得到融合后的mass函数，最后根据决策规则得到机器的故障融合诊断结果，如图6所示。

图6　融合诊断结果

可以看出，融合诊断结果较为明显的显示出机器当前所处的状态为第1类故障。

4　结论

论文讨论了一种使用多传感器数据进行机械故障诊断的方法。该方法将D-S证据理论应用到机械故障诊断的融合过程，有效的解决了诊断过程中的容错性问题。实验表明，由两传感器量测数据融合诊断的结果比由任意一个传感器独立诊断的结果在准确性上有较大程度的提高。目前，基于D-S证据理论的故障融合诊断方法基本上还处于理论研究阶段，在实际的工程应用中还有很多需要解决的问题，如传感器数量增加导致计算复杂度呈指数增长，在确定故障类型的决策阶段还没有较为统一有效的算法等。在后续的研究过程中，笔者将针对上述问题做进一步的研究和完善。

［1］梁伟光，王永，匡衡，等.融合诊断中信息容错性的证据重构方法［J］.控制理论与应用，2011，28（9）：1049-1055.

［2］王福元，徐家文，吴祥.基于多信息融合的电解加工智能故障诊断系统［J］.制造技术与机床，2005（5），37-40.

［3］Mostafaei，H.R.，Khalaj，M.，Khalaj，F.，et al.Engine fault diagnosis decision-making with incomplete information using Dempster-Shafer theory［J］.Journal of Basic and Applied Scientific Research，2012，2（1）：105-113.

［4］Dromigny，A.，Zhu，Y.M.Improving the dynamic range of real-time X-ray imaging systems via Bayesian fusion［J］. Journal of Nondestructive Evaluation，1997（16）：147-160.

［5］Basir，O.，Yuan，X.H.Engine fault diagnosis based on multi-sensor information fusion using Dempster-Shafer evidence theory［J］.Information Fusion，2007（8）：379-386.

［6］张文胜，龚涛，胡锴.基于D-S证据理论的直流电机故障诊断研究［J］.中国舰船研究，2010，5（4）：72-74.

［7］蒋玲莉，刘义伦，李学军，等.基于SVM与多振动信息融合的齿轮故障诊断［J］.中南大学学报（自然科学版），2010，41（6）：2184-2188.

［8］綦黎明，王宝庆.一种基于证据理论的多源信息融合管道泄漏诊断［J］.机床与液压，2012，40（23）：181-184.

［9］Al-Ani，A.，Deriche，M.A new technique for combining multiple classifiers using the Dempster-Shafer theory of evidence［J］.Journal of Artificial Intelligence Research，2002，17：333-361.

［10］Hoffman，J.C.，Murphy，R.R.Comparison of Bayesian and Dempster-Shafer theory for sensing：a practitioner's approach［C］.SPIE Proc.on Neural and Stochastic Methods in Image and Signal Processing，1993，2032：266-279.

［11］Yang，B.S.，Kim，K.J.Application of Dempster-Shafer theory in fault diagnosis of induction motors using vibration and current signals［J］.Mechanical Systems and Signal Processing，2006，20：403-420.

（编辑 赵蓉）

Fault Diagnosis Based on D-S Theory Using Multisensor Data

QUAN Hong-wei1，LI Jun-hua1，PENG Dong-liang2
（1.Department of Mechanical&Electrical Engineering，Xijing University，Xi'an 710123，China；2.Institute of Information and Control，Hangzhou Dianzi University，Hangzhou 310018，China）

In multisensor fault diagnosis system，a relationship between the parameter space of feature and the type space for engine fault needs to be established.Also the problem that the diagnostic results from different sensors for the same engine may conflict needs to be addressed.The method of fault diagnosis based on D-S evidence theory using multisensor data fusion can solve the problems above to a large extent.The paper first discussed D-S theory in conjunction with fault diagnosis system；then an instance of fusion diagnosis using two sensors was given；finally we compared the simulation results in single sensor with fusion diagnosis.Analysis shows that the method based on D-S theory can solve the problem of evidence conflict in multisensor fault diagnosis effectively，and improve the accuracy of fault diagnosis decision to some extent.

fault diagnosis；D-S evidence theory；multi-sensor fusion；belief function

TH165+.3

A

1001-2265（2015）02-0100-04 DOI：10.13462/j.cnki.mmtamt.2015.02.028

2014-06-08

国家自然科学基金资助（61174024）

权宏伟（1979—），男，四川广元人，西京学院讲师，博士，研究方向为多源信息融合、故障诊断，（E-mail）quanhw@126.com。