基于模糊控制的3R欠驱动机器人轨迹跟踪研究*

梁 浩，余跃庆

（北京工业大学机械工程与应用电子技术学院，北京 100124）

基于模糊控制的3R欠驱动机器人轨迹跟踪研究*

梁 浩，余跃庆

（北京工业大学机械工程与应用电子技术学院，北京 100124）

对水平运动的3R欠驱动机器人轨迹跟踪控制问题进行了研究。设计了Mamdani型模糊控制器和一种复合型Fuzzy-PID控制器，利用主、被动关节的动力学耦合规律实现对末端点的轨迹跟踪控制。复合控制器设有两个模态，当误差大于所设阀值时采用Mamdani型模糊控制以获得较高的瞬态性能，当误差小于所设阀值时采用PID控制以获得较高的稳态性能。在ADAMS中建立欠驱动机器人的虚拟样机模型，在MATLAB中建立复合型模糊控制系统，通过二者的联合仿真进行验证。结果表明：和Mamdani型模糊控制相比，复合型Fuzzy-PID控制器消除了系统的稳态误差，提高了轨迹跟踪的控制精度。

欠驱动机器人；动力学耦合；Fuzzy-PID控制；轨迹跟踪

0 引言

欠驱动机器人是独立控制输入数目少于系统自由度的机械系统，由于减少了驱动装置，具有质量轻、能耗低、仿生性强等优点［1-2］，对其进行轨迹跟踪控制在生产实践中有重大的现实意义。但由于欠驱动系统受到二阶非完整约束，其特殊的非线性结构，满足Brockett条件［3］，不存在光滑的状态反馈控制规律使系统镇定在平衡点上。因此，无法通过运动学方法直接控制被动关节，只能从动力学角度进行控制。而其被动关节的加速度仅受到来自其他主动关节的动力学约束，导致系统缺乏对任意状态空间轨迹的跟踪能力，大大增加了控制系统的设计难度。

目前，国内外一些学者针对欠驱动机器人控制问题进行了研究。Arai［4］等利用构造轨迹方法证明了平面3R欠驱动机器人是可控的，并运用反馈控制策略对其实现了位置控制。De Luca［5-6］等研究了欠驱动机器人系统的小范围局部可控性问题，并用动力学反馈线性化的方法有效的解决了四自由度两被动关节机器人的运动规划问题。朱齐丹［7］等利用平均值法对欠驱动系统进行简化，提出了一种非线性闭环反馈控制方法。刘庆波［8］等运用模糊控制理论对3R欠驱动机器人进行了位置控制研究。现有研究当中大多是基于系统的精确的动力学模型对其位置控制进行研究，对末端点连续轨迹跟踪控制的研究不多。胡毅［9］等基于模糊控制的轨迹跟踪研究当中，其参数调节复杂，且没有考虑偏差变化率，不利于对复杂控制任务的研究和控制精度的提高。

本文以模糊控制理论为基础，研究水平运动的3R欠驱动机器人末端点的轨迹跟踪控制问题。针对相同的控制任务，基于主、被动关节的动力学耦合作用设计了Mamdani型和Fuzzy-PID型（以下简称F-PID）两种模糊控制器。借助ADAMS虚拟样机和MATLAB的联合仿真对3R欠驱动机械手末端的轨迹跟踪问题进行仿真对比分析，避免了数值仿真时对复杂动力学模型的推导，结果表明；通过二维模糊控制算法能很好的完成3R欠驱动机器人的轨迹跟踪控制，控制精度高；FPID型双模态复合控制器有效降低了系统的稳态误差，进一步提高了控制精度。

1 欠驱动机械手动力学模型

水平3R欠驱动机械手臂模型的示意图如图1所示。其中第1关节和第2关节是主动关节，装有驱动装置；第3关节是被动关节（或自由关节），不安装驱动装置。对图中参数有以下规定；关节角度、角加速度、关节控制力矩（或控制电压）逆时针方向为正，顺时针方向为负；θ1、θ2、θ3代表三个关节的转角；α1为关节1和关节3的连线与杆3的夹角，α2为关节2和关节3的连线与杆3的夹角，α1、α2分别代表第三杆相对于主动杆1和主动杆2的位形参数。曲线S表示欠驱动系统运动平面内任意曲线。d表示机械手臂末端点到曲线S的法向距离。规定原点O所在一侧的点到S的法向距离为负，另一侧的点到S的法向距离为正。

由于机械手臂在水平面内运动，故不考虑重力势能项。则基于第二类拉格朗日方程建立的动力学方程为；

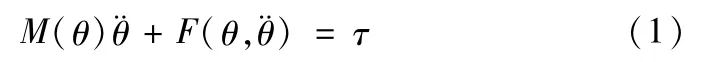
式（1）中M为质量惯性矩阵，F表示包括哥式力、离心力和摩擦阻尼在内的和角速度相关的项，θ是关节角度矩阵，т是关节驱动力矩矩阵。将式（1）展开成分块矩阵形式；

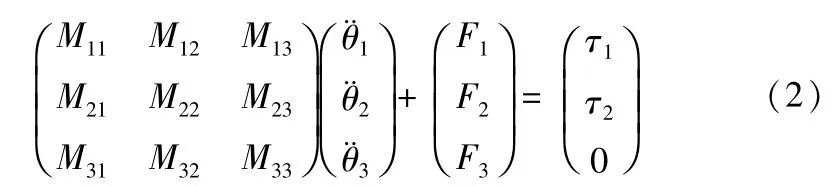
由式（2）可以看出驱动关节和被动关节的加速度之间存在耦合关系，可以通过控制各主动关节的加速度来耦合控制被动关节的运动。那么，被动关节的末端点坐标就被两主动关节的输入力矩间接控制，也就可以通过恰当的控制策略从动力学角度解决欠驱动机械手的轨迹跟踪控制问题。

2 模糊控制策略

2.1 控制原理

将欠驱动机械臂的运动分解为主动关节的旋转运动和被动关节的伸展或收缩运动。被动关节的伸缩即是两主动关节的旋转运动对被动关节动力学耦合作用的表现。要实现3R欠驱动机器人末端点的轨迹跟踪控制，就是要控制主动关节的旋转和被动关节的伸展或者伸缩，使末端点到目标轨迹S的法向距离d始终为零，并确保末端点的速度大于零。这里我们只考虑末端点轨迹的形成，不对末端点的速度和加速度作定量要求。

为了不失一般性，在自由关节处安装制动器。将轨迹跟踪控制过程分为两个阶段。第一阶段，锁定制动器，欠驱动机器人退化为全驱动，通过控制主动关节使机器人末端点从任意初始位置向目标轨迹靠近；第二阶段，当末端点第一次到达目标轨迹时制动器解锁，被动关节完全自由，开始欠驱动控制阶段。

欠驱动控制阶段的控制流程图如图2所示。两主动关节分别对末端偏差进行调控，两控制层之间相互对立。具体过程为；将 т1、т2分开考虑，单独计算т1时，视杆1和杆2相对静止，把二者看成一个整体，将d和α1作为输入变量反馈给模糊控制器1，得到关节1的输入转矩т1；单独计算т2时将d和α2作为输入变量反馈给模糊控制器2，得到关节2的输入转矩т2；最后通过动力学耦合作用共同控制末端杆件的运动，使末端点的坐标跟踪目标轨迹曲线。

由于不同的位形参数下主、被动关节的耦合规律不同，以耦合作用的基本单元二连杆为例将位形分为两类。如图3所示，位形1中α＞=0，控制力矩的正负与d相同，记为Flag=1；位形2中α＜0，控制力矩的正负与d相反，记为Flag=2。下面就两种形式的模糊控制器进行说明。

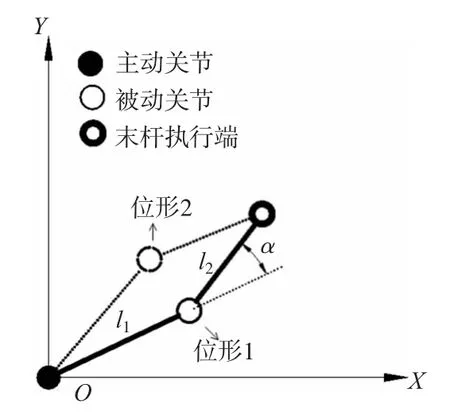
图3 二连杆示意图

2.2 Mamdani型模糊控制器设计

Mamdani型二维模糊控制器的的结构框图如图4所示。取控制器的输入量为机械手末端点到目标曲线的法相距离d及其变化率η，输出量为两主动关节的控制力矩（或控制电压）т1、т2。

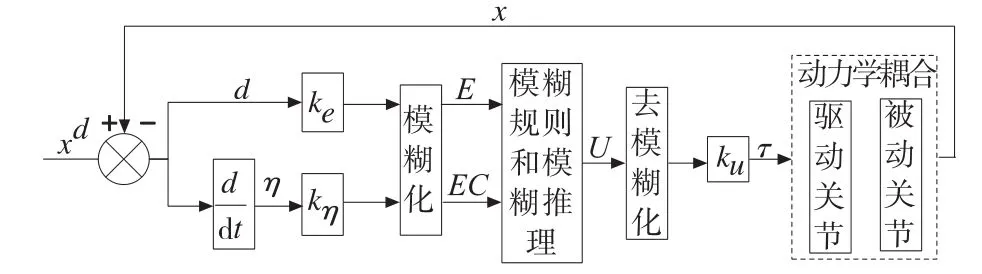
图4 Mamdani型二维模糊控制器结构框图

精确量d和η分别乘以相应的量化因子ke和kη转化到各自的论域范围。设定输入量d和输出量т论域为［-3，3］，输入量η的论域为［-1，1］。将输入量d和输出量т的论域划分成“负大”、“负中”、“负小”、“零”、“正小”、“正中”、“正大”7个模糊子集，即｛NB，NM，NS，ZO，PS，PM，PB｝。将输入量η的论域划分为“负”、“零”、“正”三个模糊子集，即｛N，ZO，P｝。

为了精确地表达动力学耦合规律，本文采用符合人脑特点、具有良好抗干扰能力的高斯函数作为隶属度函数，函数曲线如图5和图6所示。

结合动力学耦合规律和控制经验总结出模糊控制规则；当末端误差和误差变化率均为正时，对驱动关节施加较大反向转矩，利用动力学耦合作用使被动关节产生反向加速度，以补偿正向误差；当末端误差和误差变化率均为负时，对驱动关节施加较大正向转矩，以补偿负向误差。其他中间情况，根据以下原则酌情而定；当误差较大时，调节控制变量以消除误差为主；当误差较小时，调节控制量防止超调，以控制系统的稳定性为主［10］。

图5 输入量d和输出量т的隶属度函数曲线

图6 输入量η的隶属度函数曲线

表1 FLC模糊控制规则表（a）Flag=1

模糊规则采用If…then…形式表示，得到形如；“If d is NB，ηis N and Flag is 1，thenтis PM”的42条规则，如表1所示。模糊推理采用Mamdani模型中的max-min合成法。去模糊化采用精度较高的重心法。

2.3 F-PID型控制器设计

由于Mamdani型二维模糊控制器缺少积分环节，导致模糊控制器在平衡点附近存在盲区，无法消除一定的稳态误差。而PID控制具有积分环节，能够有效地消除稳态误差，有比模糊控制更好的稳态性能。下面结合Mamdani型模糊控制器和PID控制器各自的优点设计了一种F-PID复合控制器，示意图如图7所示。

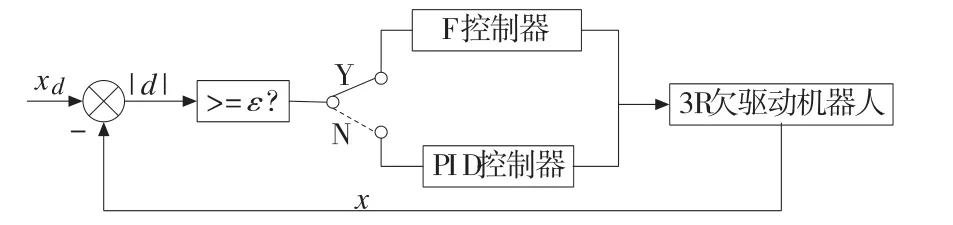
图7 F-PID复合控制器示意图

设置了一个带有阀值ε的模态转换器，根据ε与距离偏差的绝对值|d|比较结果确定模态；当|d|大于等于ε时，让信号传输到F控制器，以减小超调量，缩短调节时间；当|d|小于ε时，让信号传输到PID控制器，以消除稳态误差，获得良好的稳态性能。

图8 PID控制器结构图

F控制器部分即为一个Mamdani型二维模糊控制器，本节不再赘述。PID控制器结构图如图8所示。为了满足动力学耦合规律，PID参数试凑的总体原则是；当Flag=1时，kp、ki、kd均取负值；当Flag=2时，kp、ki、kd均取正值。

3 建立联合仿真系统

利用ADAMS/Controls模块，可以将ADAMS程序和控制分析软件MATLAB有机地连接起来，实现将复杂的控制引入ADAMS的机械系统虚拟样机中。利用三维样机模型代替繁琐的方程直观地描述机械系统，避免了单独用MATLAB进行数值仿真时大量的方程推导。

3.1 建立物理仿真模型

三维样机模型如图9所示。在靠近电机的两个转动副上添加力矩以代替电机转矩；在最后一个转动副处不施加力矩代表自由关节。

图9 水平3R欠驱动机械手三维模型

考虑各关节摩擦力对运动控制的影响，在关节处添加阻尼器，采用粘性摩擦，数学模型如式（3）所示。式中，f为摩擦力矩，μ为粘性摩擦因数，为关节角速度。

ADAMS可以实时调用控制系统输出的控制力矩的值，并同时将各关节角度和末端点的偏差反馈到控制系统，从而构成闭环控制。数据传递过程如图11所示。

图11 联合仿真系统数据传递流程图

3.2 控制系统建模

根据控制原理，在Simulink模块中分别搭建Mamdani型和Fuzzy-PID型模糊控制系统，系统框图如图13、图14所示。

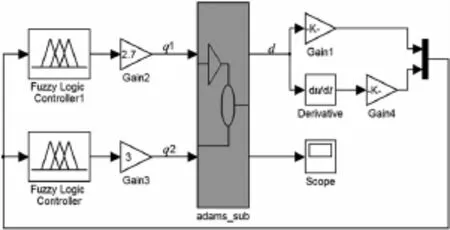
图13 Mamdani型模糊控制系统框图

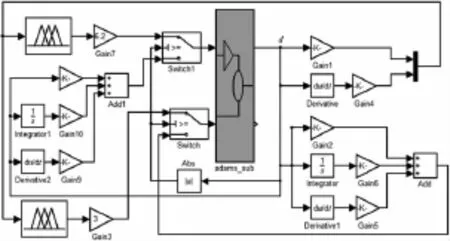
图14 F-PID型模糊控制系统框图

4 联合仿真及结果分析

取目标跟踪曲线S为直线Y=400，机械手臂的初始位姿为；关节1角度为-90°，关节2和关节3角度均为0°。第三杆末端点第一次到达Y=400之前第1、2关节的控制力矩分别为2.5N·mm、-1.2N·mm，第3关节锁死。末端点首次到达Y=400之后第3关节释放自由，各关节的控制力矩由模糊控制器确定。两种控制算法下的末端轨迹曲线如图15所示。末端点的绝对偏差对比如表2所示。

图15 Mamdani型和F-PID型模糊控制末端轨迹曲线

表2 末端点绝对偏差对比（样本点采集时间：20s～35s）

根据末端轨迹曲线和曲线偏差对比结果可以看出；Mamdani型模糊控制器下，末端轨迹误差收敛速度快，系统具有很好的瞬态性能，但绝对偏差在-2.7上下浮动，存在明显的稳态误差；F-PID型模糊控制器下，系统响应迅速，基本消除了稳态误差，末端控制轨迹的误差平均值为0.45，达到了较高的精度要求。

F-PID型模糊控制器下绝对偏差5 结束语

的标准差0.29大于Mamdani型模糊控制器下的0.18，说明F-PID型模糊控制器下误差的波动较大。这是由于在运动过程中，系统的耦合指标在不断变化，PID控制器对参数变化比较敏感。。

本文基于模糊控制策略，利用3R欠驱动机器人的主、被动关节的动力学耦合作用，设计了Mamdani型和F-PID复合型模糊控制器，完成了对水平运动的3R欠驱动机器人的末端点的轨迹跟踪的控制。利用MATLAB和ADAMS联合仿真进行控制算法的验证，避免了繁琐的动力学方程推导。仿真结果表明，这两种模糊控制器都能较好完成欠驱动机器人末端的轨迹跟踪控制。相比之下，F-PID型复合模糊控制器由于具有积分环节，消除了系统的稳态误差，使系统具有更高的控制精度。本文所用的复合型模糊控制器为欠驱动机器人的轨迹跟踪的优化控制提供了新思路。

［1］陈炜，余跃庆，张绪平.欠驱动机器人研究综述［J］.机械设计与研究，2005（4）；22-26.

［2］Spong M.Underactuated mechanical systems［M］.Siciliano B，Valavanis K，Springer Berlin Heidelberg，1998.

［3］Brockett R W.Asymptotic stability and feedback stabilization，differential geometric control theory［M］.New York，USA；Birkauser，1983.

［4］Arai H，Tanie K，Shiroma N.Nonholonomic control of a three-DOF planar under actuated manipulator［J］.Robotics and Automation，IEEE Transactions on，1998，14（5）；681-695.

［5］De Luca A，Oriolo G.Motion planning and trajectory control of an under actuated three-link robot via dynamic feedback linearization［C］.San Francisco，CA，USA；IEEE，2000.

［6］De Luca A，Iannitti S.A simple STLC test for mechanical systems under actuated by one control［C］.2002.

［7］朱齐丹，席志红.具有非驱动关节机器人的位置闭环控制［J］.哈尔滨工程大学学报，2002，23（4）；67-72.

［8］刘庆波，余跃庆.基于遗传算法的欠驱动机器人模糊控制器设计［J］.系统仿真学报，2008，20（8）；2097-2100.

［9］胡毅，余跃庆.平面三自由度欠驱动机器人轨迹跟踪控制［J］.组合机床与自动化加工技术，2012（12）；82-84.

［10］诸静.模糊控制原理与应用［M］.北京；机械工业出版社，1995.

（编辑 李秀敏）

Trajectory Tracking Control of 3R Underactuated Robot Based on Fuzzy Control

LIANG Hao，YU Yue-qing
（College of Mechanical Engineering and Applied Electronics Technology，Beijing University of Technology，Bejing 100124，China）

；To improve the control effect of the trajectory tracking of a 3R horizontal under actuated manipulator，a kind of Fuzzy-PID compound controller is designed，which realizes the control by using the dynamic coupling between the actuated and the under actuated joints.It is a dual-mode system.If the error is higher than the valve values，the fuzzy controller works in order to obtain a good transient performance.If the error is lower than the valve values，the PID controller works in order to obtain a good steady state performance. The virtual prototype system of the 3R horizontal under actuated manipulator was created in ADAMS，and the control system is designed in MATLAB.The co-simulation based on MATLAB and ADAMS for the robot was realized by the interface module between them.The results of the co-simulation show that the Fuzzy-PID compound controller can effectively reduce the control error and improve dynam ic property of the system.

；under actuated robot；dynamic coupling；Fuzzy-PID control；trajectory tracking

TH121；TG659

A

1001-2265（2015）05-0091-04 DOI：10.13462/j.cnki.mmtamt.2015.05.025

2014-09-07

国家自然科学基金资助项目（51175006）

梁浩（1991—），男，河南周口人，北京工业大学硕士研究生，研究方向为机构与机器人系统分析与控制，（E-mail）bjlh@emails.bjut. edu.cn。