现代变换通信系统降噪技术研究
王洪剑
(黄河科技学院,郑州 450063)
现代变换通信系统降噪技术研究
王洪剑
(黄河科技学院,郑州 450063)
文章采用时域和离散傅里叶逆变换域级联两种降噪方式,通过降低导频信号的噪声,由此来提升变换域通信系统信道估计值的准确性。最终的仿真结果显示:这一方法在时域降噪环境下同样有效。这为两种方法的结合降噪奠定了基础。
变换通信系统;降噪技术;离散傅里叶逆变换域
由于受低信噪比噪声的干扰,很难获得清晰、可靠的信道信息,因此,为了提高以OFDM-TDCS为基础的低信噪比的性能水平,整个系统必须拥有可靠的信道估计。基于此,文章提出了采用时域和离散傅里叶逆变换域级联两种降噪方式,通过降低导频信号的噪声,由此来大大提升变换域通信系统信道估计值的准确性。
1 以正交频分复用技术为基础的变换域通信系统
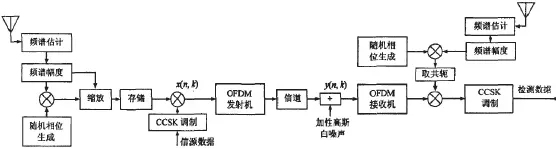
图1 基于OFDM的变换域通信系统(TDCS)结构图
其结构图如1所示,发送端的信源数据要先经过频域CCSK基函数的调制活动。该基函数主要是通过信源数据发送端频谱检测器估计所产生的频谱幅度乘以系统内的随机相位之后,并经过一系列适当的缩放活动所得。假设发送与接收两端经过检测之后所获得的频谱幅度十分理想,而且一致,然后采用普通的OFDM技术来发射信源数据。信号在该频域中可以通过以下公式进行表示:
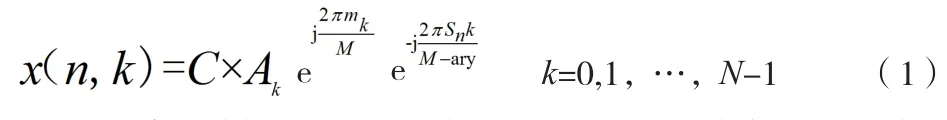
n表示发射时刻,N为基函数的长度,k表示特定的子载波,M表示随机相位矢量,x(n,k)表示第k个子载波在n时刻的发射信号,Ak则表示取值为1或0的频谱幅度矢量元素,mk是指在0至M-1之间的随机整数,Sn是指第n个发送的符号。在经历了低信噪比噪声的干扰之后,发射信号到达接收端。其所在频域可以表示为:
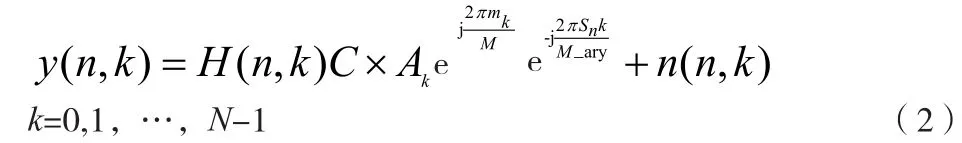
y(n,k)表示第k个子载波在n时刻的接受信号;n(n,k)表示均值为0的加性复高斯噪声;H(n,k)为第k个子载波在n时刻的信道频率响应;N0是指方差。接收信号在到达接收端之后,首先经过OFDM技术的处理,然后乘以本地生成的基函数CCSK,最后再通过该基函数解调检测出所发送的信号,作为终端信息处理的源数据,转换成所预期的信息内容。
2 以降噪为基础的信道估计
基于分析的便利性,笔者采用以块状导频图案为基础的导频辅助信道估计模型(PSAM),也即是将导频植入正交频分复用技术符号内所有的子载波中,随后再将其插入即将发送的正交频分复用技术信号中。接收机在估计导频位置的信号过程采用最小二乘法的方式,然后再使用时域以及IDFT变换域级联进行降噪活动,由此来大大提升变换域通信系统信道估计值的准确性。
2.1最小二乘法估计
最小二乘法估计是传统通信系统中获得导频位置信道系统最常用的方法,也即是将接收端接收的信号除以发送端发送的导频符号。其公式为:
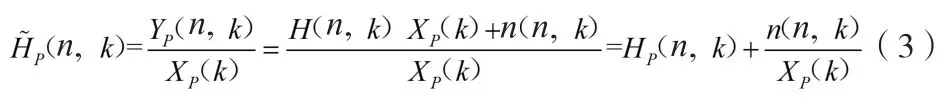
2.2时域降噪方式研究
2.2.1时间滑动平均降噪法
在IEEE 802.22无线区域网(WRAN)系统之中,信道系数变化非常慢,因此,可以假设N个正交频分复用技术导频符号的信道系数保持不变。其公式为:

针对这种信道系数变化较慢的情况,对N个正交频分复用技术导频符号所对应的子载波的最小二乘法估计信道系数进行取平均计算,被称为是时间平均降噪法。其计算方式为:
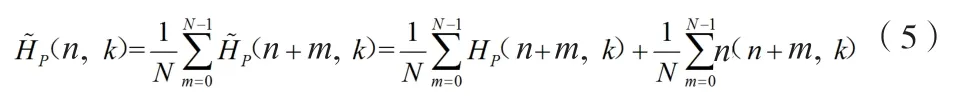
由于在不同的时间,噪声之间呈现出分隔、独立的状态,由此可知此时刻的噪声方差仅仅是最小二乘法估计的1/N。然而,这种计算方式只局限于特定的求平均需要,但不同位置的信道估计值呈现出迥异的延时性特征。因此,为了使估计的信道系数具有相同的时延,可采用时间滑动的平均降噪方式来实现这一目的,也即是将第n个导频符号所对应子载波信道系数的估计值,通过n-(N/2),…,n,…,n+[(N-1)/2]时刻所对应的导频子载波的最小二乘法估计的平均值来进行表示。在此过程中,可以将不大于a的最大整数视为[a]。这一信道系数的估计方法可以表示为:
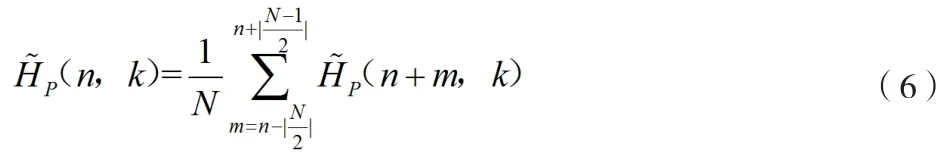
2.2.2时间遗忘降噪方式
上文分析的时间滑动平均降噪与时间平均降噪所计算出的信道系数都呈现出时延性的特征,也即是信道系数之间具有明显的时间间隔特征,因此,根据这一特点,可采用时间遗忘降噪的方式来估计信道系数。该方法的最大优点就在于对缓存导频数据没有过多的要求,能够实时处理系统内的导频数据。
具体来说,时间遗忘降噪方式也即是通过前一时刻估计的信道系数按权相加当前时刻运用最小二乘法所获得的信道系数,计算结果作为当前时刻估计的信道系数。其计算方法为:

其中,0<α≤1。该公式假设不同时刻的信道系数也不相同,因此,各个时刻通过最小二乘估计所获得的信道系数应对当前所计算出的信道系数呈现出迥异的权值,与当前时刻越近,其信道估计值也就越有可能相等,因此也就表现出更大的权值。正如上文所说,在不同的时间,噪声之间呈现出分隔、独立的状态。基于此,某一时刻(假定为n)的信道估计方差同最小二乘估计的噪声方差之间的比值公式为:
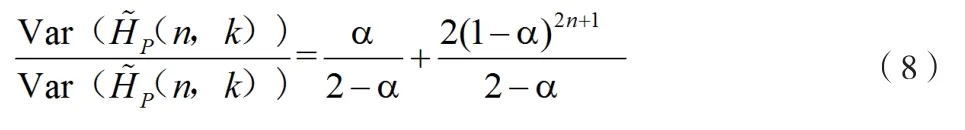
信源数据接收端需要接收一段导频符号之后,n时刻的信道估计方差同最小二乘估计的噪声方差之间的比值才能达到收敛值α/(2-α)的水平。最开始的一段时间内计算出的信道估计值并不准确,因此,在减小时延的过程中,可以将时间平均降噪和时间遗忘降噪联合起来,从而大大提升信道估计的准确性。在此过程中,可采用两种方式实现:一是采用时间平均降噪来处理最开始接收到的信源数据,当信道估计值比较准确的时候再实施时间遗忘的降噪方法;二是在每收到M个导频符号之后,通过时间平均的方式计算出均值,然后采用时间遗忘算法按权相加前一段时刻的信道估计值,并将此结果作为最终的信道估计值。
3 离散傅里叶逆变换域降噪
时间遗忘降噪法和时间滑动平均降噪法都是建立在慢衰落信道在时延过程中的缓慢变化特征的基础之上而进行的信道估计,而离散傅里叶逆变换(IDFT)域降噪则是通过多径时延集中在整个时隙的前一段的特征而进行的信道估计活动。其实现过程为:先将前面几种时域降噪方法计算之后得到的估计值(n,k)或者是最小二乘估计值(n,k),通过离散傅里叶逆变换到时域。由于多径时延主要是集中在前一阶段中的时隙,因此,这一段时隙也包含了时域的信道系数,而噪声能够扩展至整个时隙,因此,可通过并不复杂的滤波的方式,通过前一段时隙,将后一段时隙设置为0,由此大大降低噪声对信道估计的干扰或影响等。
4 结 语
最终的基于时域和IDFT降噪技术的仿真结果表明:本文提出的以时域和离散傅里叶逆变换(IDFT)域联合降噪的方法呈现出良好的降噪性能,尤其是时间遗忘降噪与时间平均降噪相结合的两方计算方式不仅大大提升了信道估计的精确性;还极大减小了时延, 提高了通信系统的运行质量和效率,呈现出良好的实用价值。目前,这种降噪方式在理论上具有明显的可行性价值,然而如何应用于实际的通信活动中还有待进一步的研究。这将是该课题进行下一步研究的方向。
主要参考文献
[1]沙学军.分数傅里叶变换原理及其在通信系统中的应用[M].北京:人民邮电出版社,2013.
[2]张智林,皮亦鸣,孙志坚.基于独立分量分析的降噪技术[J].电子科技大学学报,2005(3).
[3]包兴先,刘福顺,李华军,等.复指数方法降噪技术及其试验研究[J].中国海洋大学学报,2011(1).
[4]李方,李友荣,王志刚.基于Morlet小波与最大似然估计方法的降噪技术[J].振动、测试与诊断,2005(1).
10.3969/j.issn.1673 - 0194.2015.20.089
TN914
A
1673-0194(2015)20-0113-02
2015-08-27

