生成分支q-矩阵的Feller性质
张秀珍,薛桂兰,乔世东,张洁萍
(1.山西大同大学数学与计算机科学学院,山西大同037009;2.山西大同大学煤炭工程学院,山西大同037003)
生成分支q-矩阵的Feller性质
张秀珍1,薛桂兰2,乔世东1,张洁萍1
(1.山西大同大学数学与计算机科学学院,山西大同037009;2.山西大同大学煤炭工程学院,山西大同037003)
研究了生成分支q-矩阵,得到了该矩阵Feller性的充要条件。
q-矩阵;生成分支q-矩阵;Feller;强零流入
近年来,许多专家学者们对于生成分支过程做出了不少的研究,比如生成分支过程的遍历性,见文献[1-2]。本文就生成分支q-矩阵
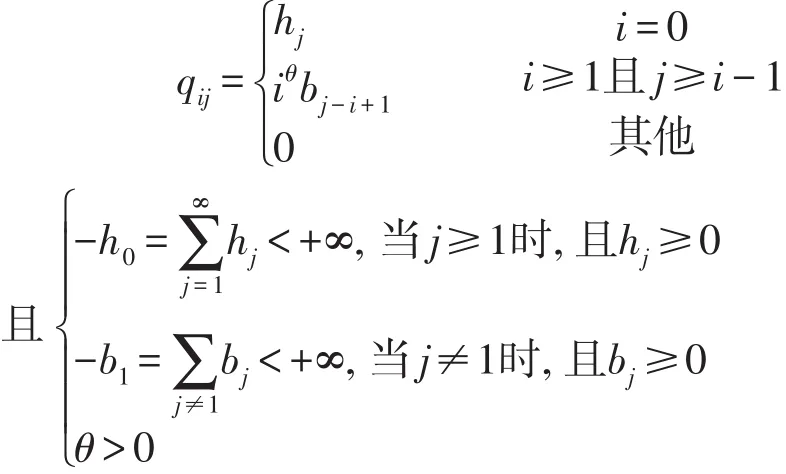
的Feller性进行研究。
1 预备知识
若qij→0,当i→∞时,j∈E={1,2,3,…},则称 q-矩阵是Feller的;
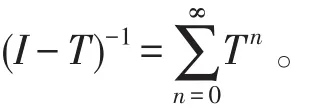
2 主要结论
定理1设生成分支q-矩阵Q=Q*+A,其中Q*是一个单调的q-矩阵,A是一个Feller的且行和有界的矩阵,也就是,则Q是强零流入的当且仅当Q*强零流入。
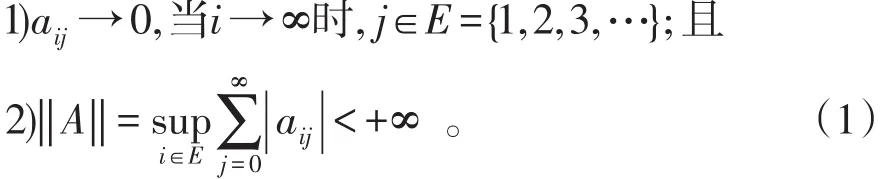
证明 Q,Q*可在l1上分别诱导出算子Q1,Q*1,并定义如下:
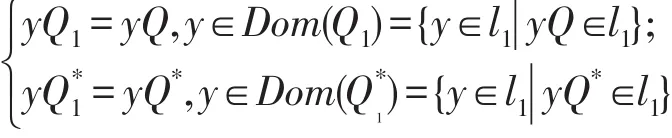
其中y是行向量。令Ω是由最小Q-函数诱导的连续压缩半群P(t)的生成元,则Ω⊂Q1,也就是,Ω是Q1的限制。因而λI-Ω⊂λI-Q1。由已知条件强零流入得λI-Q1是单射,这意味着,λI-Ω=λI-Q1,因而
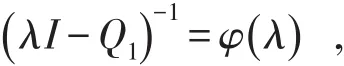
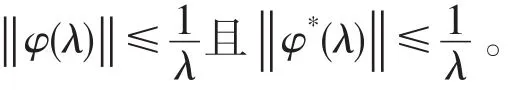
选取 λ0满足,则由巴拿赫定理得,
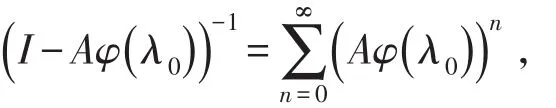
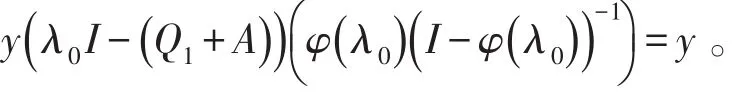
定理2生成分支q-矩阵Q仍分解成如定理1的形式,则最小Q-函数P()t是Feller转移函数的充要条件是最小的Q*-函数P*(t)也是Feller的。
证明P*(t)是Feller的,则最小Q*-豫解φ*(λ)也是Feller,因而φ*(λ)在c0上诱导一个有界算子。取λ0满足,则由巴拿赫定理知,在存在且
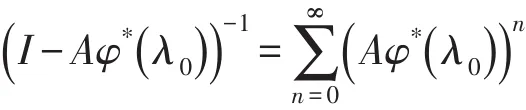
也就是对任意的x∈c0,
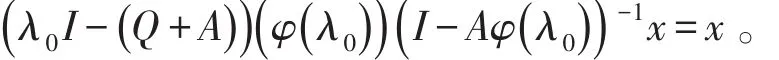
因而λI-Q是c0上的满射。因而最小的Q*-函数P*(t)是Feller的。反过来取Q*=Q-A可类似地证明。
定理3对生成分支q-矩阵Q,最小Q-函数是Feller的当且仅当Q是Feller且强零流入的。
证明由于生成分支q-矩阵Q=Q*+A,Q*是一个单调的q-矩阵,A是一个Feller的且行和有界,由最小的Q*-函数是Feller的当且仅当单调q-矩阵Q*是Feller且强零流入的,最小Q-函数是Feller的当且仅当Q是Feller且强零流入的。
[1]ANDERSON W J.Continuous Time Markov Chains[M].New York:Springer-Verlag,1991.
[2]CHEN A Y.Ergodicity and stability of generalized Markov branching processes with resurrection[J].Appl Prob Letters,2002(39):786-803.
[3]YOSIDA K.Function Analysis[M].New Yourk:Springer-Verlag,1978.
[4]LI Jia,LI Yangrong.Criteria for Feller transition functions[J].Math Anal Appl,2009(359):653-665.
The Feller Property of Generalized Branching q-matrix
ZHANG Xiu-zhen1,XUAN Gui-lan2,QIAO Shi-dong1,ZHANG Ji-ping1
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009;2.School of Coal Engineering,Shanxi Datong University,Datong Shanxi,037003)
In this paper,we will obtain a sufficient and necessary condition of the Feller property of the generalized branching q-matrices.
q-matrices;generalized branching q-matrices;Feller;zero-entrance
O175
A
1674-0874(2015)05-0018-02
2014-05-24
张秀珍(1984-),女,山西大同人,硕士,助教,研究方向:泛函分析。
〔责任编辑 高海〕

