A novel Q-based online model updating strategy and its application in statistical process control for rubber mixing

Chunying Zhang,Sun Chen,Fang Wu,Kai Song*

School of Chemical Engineering and Technology,Tianjin University,Tianjin 300072,China

Keywords:Online model updating Rubber mixing Q statistic Hardness Rheological parameters Statistical process control

A B S T R A C T To overcome the large time-delay in measuring the hardness of mixed rubber,rheological parameters were used to predict the hardness.A novel Q-based model updating strategy was proposed as a universal platform to track time-varying properties.Using a few selected support samples to update the model,the strategy could dramatically save the storage cost and overcome the adverse influence of low signal-to-noise ratio samples.Moreover,it could be applied to any statistical process monitoring system without drastic changes to them,which is practical for industrial practices.As examples,the Q-based strategy was integrated with three popular algorithms(partial least squares(PLS),recursive PLS(RPLS),and kernel PLS(KPLS))to form novel regression ones,Q PLS,Q RPLS and Q KPLS,respectively.The applications for predicting mixed rubber hardness on a large-scale tire plant in east China prove the theoretical considerations.

1.Introduction

In rapidly developing rubber industry,it is urgent to improve the control performance of rubber mixing process,the fi rst key step in a rubber manufacturing process.How ever,the large time-delay for measurement of hardness,one of the most important quality indexes of mixed rubber,has long been the main deterrent for further development of the control system for rubber mixing.The conditioning time of mixed rubber before sampling for measuring hardness is usually about 2–4 h,which is much longer than rubber mixing time(2–5 min),while it is possible to obtain rheological parameters of mixed rubber in several minutes(about 2 min)with the online rheological instrument.With the mechanism of rubber mixing,there must be certain relationship between hardness and rheological parameters.Hence,we propose a hardness prediction model using the rheological parameters.

Lacking of the mechanical knowledge of rubber mixing,the hardness prediction is a typical“black-box”issue.Data-driven methods present outstanding performance in modeling “black-box”processes and they are attractive options to resolve the relationship between hardness and rheological parameters[1,2].For example,principal component analysis(PCA),partial least squares(PLS)and their generalized methods are powerful techniques for modeling “black-box”processes[3–7].For most regular data-driven methods,how ever,one of the main defects is that they cannot track time-varying properties of the process,affecting their prediction precision and weakening their applications in the hardness prediction.

To solve this problem,several model updating methods have been developed.The recursive partial least squares(RPLS)method has been widely applied in industrial practices since it was proposed by Hell and et al.in 1992[8–11].How ever,RPLS cannot overcome the “data saturation”and cope with abrupt changes in process characteristics.The time and memory requirements of the RPLS method will become larger and larger along with the process.Choi et al.[12]proposed an adaptive PCA method,which could update model by recursive formulas composed of updated mean,variance and covariance of samples.How ever,PCA could only extract principal components from independent variables.As a result,PCA-based methods often fail in the quality predictions.To cope with the nonlinear properties of time-varying systems,several nonlinear model updating methods have been developed.As a useful nonlinear data-driven modeling method,neural network has been modified to update models[13].An online weighted least squares support vector machine method was proposed by Tang et al.to track the process[14].However,as typical multi-parameter methods,the negative effects are the large time and storage costs for optimizing the model parameters.Furthermore,all of these model updating methods are appropriate for certain algorithms,so their practicability is quite limited.To deal with increasingly complicated industrial processes,more practical and simpler model updating strategy is needed.

On the other hand,it is essential to ensure the operation stability and safety of rubber mixing processes,so fault diagnosis and isolation are fundamental functions of statistical process monitoring(SPM)systems[15,16].According to the mechanisms of the two statistics,it is the Q statistic instead of T2statistic that plays a major role in the SPM system.For simplicity,T2statistic is never taken into account in some cases.Hence,we propose a novel Q-based strategy as a universal method to update data-driven models.From the concept of support vectors of the SVM method,only a few support samples with Q values in the two optimized control limits are selected to update models.Consequently,the time and storage loads of the updating procedure can be dramatically reduced.In addition to overcome the adverse influence of low signal-to-noise ratio samples,this method can incorporate the function of model updating with that of process monitoring.Thus it can be applied to any existing SPM system without drastic changes.Such advantage is attractive in industrial practices.To illustrate the proposed Q-based strategy by examples,two widely used linear algorithms(PLS and RPLS)and one state-ofthe-art nonlinear algorithm(kernel partial least squares(KPLS))are used.We integrate them with the Q-based strategy to develop novel regression algorithms:Q PLS,Q RPLS and Q KPLS.For further test,they are applied to the hardness prediction model for rubber mixing processes.

2.Methodology

2.1.Q-based model updating strategy

SPM is an essential part in the statistical process control(SPC)for modern industrial processes.Q statistic(also called squared prediction error,SPE)is one of the most widely used control parameters in SPC[17].It evaluates the variation information that is not captured by the established model.The Q statistic can be calculated through linear models(such as PCA and PLS)and nonlinear kernel-based models(such as kernel PCA[18,19]and KPLS[19,20]).Apart from Q statistic,Hotelling's T2statistic is also well known,which is a generalization of student's t statistic[21].Since T2statistic mainly quantifies the distances between new samples and the center of the normal operation region in model space,it is often used to identify the unusual variability of the calibration model[22].If Q value exceeds the control limit,it generally indicates that the relationship of variables under the normal condition is destroyed,i.e.the established model is invalid.It means that system malfunction occurs or the operation status changes abruptly.However,if the T2value exceeds its control limit while Q value remains within its control limit,it means that some acceptable variations occur in the process and the captured relationship among variables approximately satisfies the current condition.As a result,in SPM practices,it is the Q statistic that plays the major role.For simplicity,T2statistic is usually not taken into account.

In order to adapt to industrial development,several new methods have been developed to improve the performance of SPM.For example,Chen et al.[23]and Yu and Qin[24]used the Gaussian mixture model to estimate the probability density function of the nominal process.How ever,most of these methods are based on the traditional statistics,in which making good use of exiting Q statistic to help update datadriven models is practical and effective.Under such circumstances,we propose a mechanism based on the Q statistic to select updating samples,to improve the predictive performance of data-driven models for on-line process monitoring.

For a linear model,given a new observation xi,the Q value is calculated by[25]

w here^xiis the reconstructed/prediction vector of xi,eiis the corresponding residual vector,Q statistic generally approximates the Chisquare distribution(χ2distribution),g is a constant,and d is the effective freedom degree of χ2distribution.

The operation condition is considered normal when the Q value of observation xisatisfies

w here Qαis the control limit(or threshold)of the Q statistic and α denotes the confidence level.In practice,χ2distribution of the Q value is usually approximated as normal distribution.Therefore,α is always set to 99%or 95%[15].For a given confidence level α,the SPE control limit can be expressed as

where Cαis the threshold of normal distribution at the confidence level of α,parameters θi(i=1,2,3)and h0are defined as

where λj(j=v+1,v+2,…,r,which satisfies λr≤ … ≤ λj≤λv+2≤λv+1)is the j th eigenvalue of R.In PLS model,is the correlation coefficient matrix of input variables X(here m is the number of samples in X).Parameter v is the number of retained latent variables and r is the number of all potential latent variables(r≤n,n is the number of training input variables).

Since the Q statistic quantifies the variation information that cannot be explained by the established model,a change in the relationship between input and output variables increases the corresponding Q values.The control limit of Q statistic indicates the allow able range,within which the deviations are assumed to be caused by random process noises or acceptable model errors.Reasonably,the samples with Q values equal to or slightly less than the control limit should be treated as critical samples,which contain the maximum allow able variation information of the process operation status.From the concept of support vectors of the SVM algorithm,such critical samples could be treated as support samples.Compared with using all new samples,using these support samples to update models will be an effective and simple method.On such an assumption,the new Q-based online model updating strategy is developed as a universal platform to update data-driven models.Meanwhile this strategy can successfully integrate model updating function with process monitoring function.Thus it is practical to relate the problem to industrial process control.

The main procedure of the proposed Q-based strategy is presented in Fig.1.

(1)If Qαh≤Qnewi,the corresponding new observation xiis treated as the outlier or abnormal sample,which should not be used to update the prediction model.

(2)If Qαl＜ Qnewi＜ Qαh,though sample xiis not an outlier,it is preferable to abandon it due to its low signal-to-noise ratio.

(3)If Qnewi＜ Qαs,sample xicontains little variation information,which should be neglected in order to save time and storage costs of the updating procedure.

The procedure of the Q-based online model updating strategy is as follow s.

(1)Build the initial data-driven model using the regression algorithm of the existing SPM.

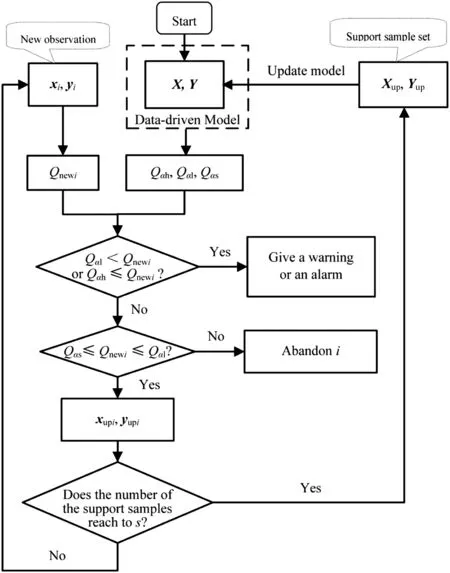
Fig.1.The main procedure of the proposed Q-based strategy.

(2)Optimize the confidence levels(αh and αl)of the control limits Qαh(alarming limit)and Qαl(warning limit)using the regular SPM method.

(3)Optimize the confidence level αs of the selecting limit Qαs.αs should satisfy the condition:αs≤ αl≤ αh.

(4)Calculate corresponding control limits Qαhand Qαlusing the regular SPM method.

(5)Calculate the corresponding selecting limit Qαs.

(6)Calculate the Q statistic value of the new observation xi:Qnewi=‖xi−‖2,where^xiis the prediction vector of xi.

(7)Operate the regular process monitoring using Qαhand Qαl.If the operation situation is normal,go to next step;otherwise,give a warning or an alarm.

(8)If Qαs≤Qnewi≤Qαl,the corresponding new observation xiis selected as support sample.

(9)If a given number(such as s)of new support samples is accumulated,update(retrain)the data-driven model and return to Step 4;or else store the obtained support samples and return to Step 6.The value of s should be decided according to the output of the practical process(in our study,s=30).

It is worth noting that Steps 1–7(except Steps 3 and 5)are the regular procedure of SPM.Obviously,it could be applied to any existing SPM system without drastic changes to it.Thus it is practical in industrial practice.Moreover,such model updating method can make good use of the existing Q statistic instead of aggravating the calculation burden or complexity to calculate other parameters.

The optimization of Qαsfor the Q-based online model updating strategy is important.If Qαsis too low,more new samples will be selected,so more time and storage space will be wasted.At the extreme,if Qαs=0,all normal new samples are treated as support samples.This makes the Q-based method lose superiority in improving prediction precision and reducing time and memory requirements.On the contrary,if Qαsis too high,few samples are selected.The prediction precision will be reduced due to a lack of variation information remaining in such samples.

So far,several parameter optimization techniques are available for the optimization of Qαs,such as particle sw arm optimization[26],genetic algorithm[27],simulated annealing[28],cross-entropy[29],reactive search optimization[30],and extremal optimization[31].Although these optimization methods offer higher accuracy in certain circumstances,the improvements may not justify the heavy computational burdens they impose for training models.Moreover,the optimization procedures need sufficient prior information from the samples or the process,which is impractical in industrial practices.In our study,we choose the simple and effective cross-validation method to optimize Qαs.

2.2.The proposed prediction model

The most widely used linear algorithm PLS and a nonlinear algorithm KPLS are chosen as examples to show the procedure of integrating Q-based strategy with them into new Q PLS and Q KPLS algorithms.To compare the modeling updating performance,we also used RPLS as an example,whose corresponding Q-based improved algorithm is Q RPLS.

2.2.1.QPLS algorithm

PLS is a popular multivariate statistical analysis tool.It creates orthogonal latent variables(LVs),which are linear combinations of the original variables[32].The basic point of the procedure is that the w eight used to determine these linear combinations is proportional to the maximum covariance among input and output variables.By projection of the PLS algorithm,the n-dimensional X-space is compressed into the v-dimensional LV-space(in common cases,v≪n,w here v is the number of the chosen latent variables)to remove the noise and the multi-colinearity inherit in X.

Q PLS regression algorithm integrates our proposed Q-based strategy with PLS to overcome the lack of model updating power of PLS.The main point is to use Q-based strategy to select support samples from new available samples.The support samples are then used to update the existing PLS model.Its procedure is described as follow s.

(1)Scale the training dataset{X,Y}to zero mean and unit variance.(2)Establish the initial PLS model｛ X，Y｝T，W，P，B，V｛

｝,where T and W are the score and weight matrices of input matrix X,respectively,P and V are loading matrices,and B is the regression coefficient matrix of the model.

(3)Optimize the confidence levels(αh and αl)of the control limits Qαh(alarming limit)and Qαl(warning limit)by the regular PLS algorithm.

(4)Optimize the confidence level αs of the selecting limit Qαs.αs should satisfy the condition:αs≤ αl≤ αh.

(5)Calculate the corresponding control limits Qαhand Qαlby the regular PLS algorithm.

(6)Calculate the corresponding selecting limit Qαs.

(7)When a block of new dataset{Xnew,Ynew}is available,calculate the Q value of the i th observationT he prediction vector of xiis expressed as

(8)Operate the regular process monitoring using Qαhand Qαl.If the operation situation is normal,go to next step;otherwise,give a warning or an alarm.

(9)If Qαs≤ Qnewi≤ Qαl,the corresponding observation xiis selected as support sample.The support sample set can be written as{Xup,Yup}.

(10)After a given number(s=30)of support samples are accumulated,update the model using{Xup,Yup}and return to Step 5;or else store the obtained support samples and return to Step 7.

2.2.2.QRPLS algorithm

RPLS allows an existing PLS model to be updated as new samples are available.The RPLS sub-model constructed with dataset{Xi,Yi}(i=1,2,…,l)is equivalent to the model established by PLS with dataset{Xblock,Yblock},with the matrices expressed as

w here Piand Viare loading matrices of Xiand Yi,respectively.All such sub-models should meet the condition of‖Ek‖≤ ε,w here Ekis the residual matrix of Xk,k is the number of latent variables,rank(X)≤k≤n and ε＞0 is the error tolerance,which is an infinitesimal positive value.The modeling process of RPLS algorithm uses all of the normal new observations to update model,so the memory requirement of updating procedure inevitably becomes larger and larger.More importantly,the current information contained in new samples will be buried in old data,known as“data saturation”.The model will soon lose the updating power in the operation of process[33].

In Q RPLS,combined with the Q-based updating strategy,comparatively smaller size of model updating samples(support samples)effectively lightens the time and memory loads of modeling procedure and reliefs the interference of“data saturation”to a certain extent.

The core procedure of the Q RPLS method is as follows.

(1)Scale the training data set{X,Y}to zeromean and unit variance.

(2)Establish the initial RPLS model:｛X ，Y ｝｛T，W，P，B，V｝,until‖Ek‖≤ ε(ε ＞ 0 is the error tolerance).

(3)Calculate the control limits Qαh(alarming limit)and Qαl(warning limit)by the regular RPLS method.

(4)After obtaining a block of new data set{Xnew,Ynew},calculate the Q value of the i th sample,xi,according to.The reconstructed vector of xiis calculated byis the corresponding regression coefficient matrix.

(5)Operate the regular process monitoring using Qαland Qαh.If the operation situation is normal,go to Step 6;otherwise,give a warning or an alarm.

(6)Optimize the selecting limit Qαsby the cross-validation method.Qαsshould satisfy the condition of Qαs≤Qαl≤Qαh.

(7)If Qαs≤Qnewi≤Qαl,the corresponding new observation xiis selected as support sample.The final support sample set can be written as{Xup,Yup}.

(8)Scale the data set{Xup,Yup}according to Step 1 and reestablish the RPLS model:where all of the parameters have the same meaning as Step 2.

2.2.3.QKPLS algorithm

KPLS is a kernel based generalized algorithm of PLS,which integrates the kernel function with the regular PLS method[34].The key idea of KPLS is to map the data of original space into a high-dimensional space(Hilbert space F),and then use the linear PLS method to detect the relationship between input and output variables.The nonlinear problems in the original space will become linear problems in the high-dimensional feature space after the projection.The nonlinear problem is easily solved by the KPLS method.

In Q KPLS,the calculation for the Q value of kernel based methods is almost in the same way as the Q PLS algorithm except for using the mapped vector Φ(xi)in F space instead of xi.Similar to Q PLS and Q RPLS,the main procedure of Q KPLS is illustrated below.

(1)Scale the training data set{X,Y}to zero mean and unit variance.

(2)Establish the initial KPLS model using the normalized data set.

(3)Calculate the control limits Qαh(alarming limit)and Qαl(warning limit)using the regular KPLS method.

(4)When a block of new data set{Xnew,Ynew}arrives,for new observation xi,calculate Qnewiin accordance with equation of Qnewi=The prediction vector of^Φ（ xi）could be calculated byKiBX,w here BX=U(TTKU)−1TTX is the regression coefficient matrix,kernel functions can be expressed as Ki=K(xi,X)and K=K(X,X).

(5)Operate the regular process monitoring using Qαland Qαh.If the operation situation is normal,go to Step 6;otherwise,give a warning or an alarm.

(6)Optimize the selecting limit Qαs(which satisfies the condition of Qαs≤Qαl≤ Qαh)by the cross-validation method.

(7)If Qαs≤Qnewi≤Qαl,the corresponding observation xiis selected as support sample.The fi nal support sample set can be written as{Xup,Yup}.

(8)If a given number(e.g.30)of support samples is obtained,return to Step 1 to update the model using{Xup,Yup};or else store the obtained support samples and return to Step 4.

3.Application and Discussion

3.1.Rubber mixing process

As the core step of a rubber manufacturing process,rubber mixing largely accounts for the quality of rubber products[35].Several parameters are used to evaluate the quality of mixed rubber and the performance of rubber mixing process control system.Among these quality parameters,hardness and rheological parameters are the most important ones.Theoretically,hardness can be measured by a type A Shore durometer after being vulcanized for about 2 h,but due to the limit of industrial practices,the measurement time-delay of hardness is often as long as 4–8 h.Such time-delay is much longer than the operation time(commonly 2–5 min)of the rubber mixing process.This obviously hinders the development of its process control system.

Rheology is the flow of fluids and deformation of rubber under various stresses and strains.Rheometer can measure material behavior such as yield stress,kinetic properties,complex viscosity,modulus,creep,and recuperability.It is possible to obtain the rheological parameters by using online rheometer within 2 min.The key rheological parameters measured in this case are listed in Table 1[36].

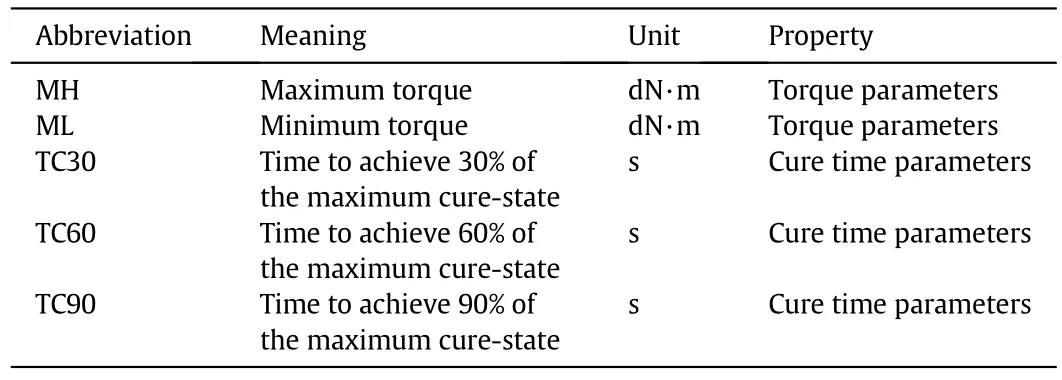
Table 1The measured rheological parameters

According to the mechanism of rubber mixing and the meanings of the two quality parameters,there must be certain relationship between hardness and rheological parameters.Consequently,it is reasonable and practicable to use the rheological parameters to predict the hardness to reduce its large time-delay in measurement.Hence,we propose the hardness prediction model with the rheological parameters as predictors.

The for mulae and manufacturing processes of all-steel rubber and semi-steel rubber are quite distinctive.In order to accurately verify the prediction of the Q-based strategy in updating the hardness model,the samples of these two mixed rubbers are used.Without causing ambiguity,the mixed rubber used for making all-steel Ridial tires and semi-steel Ridial tires are called all-steel rubber and semisteel rubber,respectively.All data are sampled in a large tire factory located in east China.Because many factors(such as properties of raw rubber and additives and climate factors)could affect rubber mixing and further the relationship between hardness and rheological parameters,the sampling period is from June 2009 to February 2010.In our case study, five rheological parameters are measured for semi-steel rubber:MH,ML,TC30,TC60 and TC90;four rheological parameters are measured for all-steel rubber:MH,ML,TC30 and TC60.Dataset-1 contains 1130 samples of semi-steel rubber and dataset-2 contains 830 samples of all-steel rubber.According to the output of the two mixed rubbers in this tire factory,the two datasets are divided into sub-blocks per 100 samples in time sequence excepting the first 30 samples:dataset-1 and dataset-2 are divided into 11 and 8 sub-blocks,respectively.

The root-mean-square-error(RMSE)and mean RMSE(MRMSE)are used to evaluate the prediction accuracy of these regression algorithms.The definition of RMSE is

w here Yiis the observation vector of the i th sub-block,Ŷiis the corresponding prediction vector,and m is the number of samples in each sub-block.For each dataset,the MRMSE is the mean of the prediction RMSE values of all the sub-blocks.

3.2.Prediction comparison of Q-based methods and corresponding regular methods

Table 2 show s the best prediction results of the proposed Q PLS,Q RPLS and Q KPLS algorithms and corresponding regular PLS,RPLS and KPLS algorithms.For the Q-based methods,the confidence levels(warning confidence level αl,selecting confidence level αs)of SPE are listed as MRMSE values.Considering the strong nonlinearity of rubber mixing process and the high noise introduced by sampling and measuring processes,αl is set to 0.90 or 0.85.To verify the practicability of the Q-based methods,the same confidence levels are used in our study.Smaller RMSE indicates smaller differences between the predicted and measured hardness values.For dataset-1,the improvements in prediction accuracy of Q PLS,Q RPLS and Q KPLS algorithms are 3.60%,11.10%and 5.94%,respectively;for dataset-2,they are 1.87%,5.50%and 4.80%.Thus the prediction performance of Q-based algorithms is much better than that of the regular algorithms.Since the rubber mixing process is a highly nonlinear process,KPLS improves the prediction accuracy incomparison with PLS.The prediction accuracy of Q KPLS is only slightly better than that of Q PLS,which is likely due to the limited sample size of each sub-block.For the two datasets,the differences in the prediction accuracies between PLS and KPLS are about 0.01 A and those between Q PLS and Q KPLS are about 0.05 A.Larger difference indicates a good effect of our Q-based strategy.

Table 2Prediction performance of Q-based methods and corresponding regular methods

For dataset-2,the MRMSE of Q RPLS is a little larger than that of Q PLS.Fig.2 shows the Q values calculated by the Q PLS method of the second sub-block samples of dataset-2.It is known that the LVs corresponding to very small eigenvalues should be removed as the noise.By doing this,PLS,PCAand other such kind of algorithm could overcome the influence of noise and the over- fitting of model[37,38].According to the methodology of RPLS,its number of LVs should be equal to the rank of the input matrix.That is,RPLS sacrifices the ability of overcoming the noise and over- fitting for the updating performance[8–10].Integrated with the Q-based model updating methodology,Q PLS can also self-update with new support samples.Fig.2 reveals that abnormal samples occur frequently,since the rubber mixing process is a high noise process.For such a high noise problem,the prediction performance of Q PLS is better than that of Q RPLS.It also proves that integrating the function of online process monitoring with the model updating strategy is important for rubber mixing.In Fig.2,the samples between the warning limit and the selecting limit are selected as the support samples.It can be found that the number of support samples is 47 for this sub-block.Since it is larger than the given updating set size s(s=30),the model will be updated by these support samples.Unlike regular PLS algorithm,using the support samples rather than all 100 new samples to update the model,the Q PLS algorithm could dramatically reduce the time and storage loads of the updating procedure.

For a further comparison,Fig.3 show s the prediction RMSE of each proposed Q-based algorithm and the corresponding regular algorithms for dataset-1.The comparison of dataset-2 is shown in Fig.4.The prediction RMSE values of the Q-based algorithms are more stable than those of the regular algorithms.

The prediction RMSE values of all the sub-blocks are listed in Appendix Table A1 for dataset-1 and Appendix Table A2 for dataset-2.Most of the prediction RMSE values by the Q-based algorithms are smaller than that by the regular algorithms.Although there are a few exceptions,the decrease in prediction accuracy of the Q-based algorithms is so small that it may be neglected.Appendix Table A1 show s that for the fourth sub-block,the decrease in the prediction accuracy of Q PLS compared with PLS is only 0.0257 A.Similarly,the prediction accuracies of Q RPLS and Q KPLS are 0.0149 A for the fifth sub-block and 0.0144 A for the fourth sub-block,respectively,which are smaller than that of RPLS and KPLS.How ever,for the last sub-block,the improvement in the prediction accuracy of Q PLS compared with PLS is 0.3958 A.The maximum improvement of prediction accuracies of Q RPLS and Q KPLS is 0.4084 A for the ninth sub-block and 0.3421 A for the eighth sub-block,respectively,compared with that of RPLS and KPLS.Similarly,Appendix Table A2 shows that in some cases the prediction precision of Q-based algorithms is not as good as that of the corresponding regular ones.For example,for the fourth sub-block,the decrease in prediction accuracy of Q PLS is 0.0657 A,and that of Q RPLS and Q KPLS is 0.0216 A for the third sub-block and 0.0330 A for the seventh sub-block.However,the superiority of the Q-based method is still obvious.For example,compared the results of Q RPLS with those of regular RPLS,the improvement is0.3909 A for the seventh sub-block;compared to PLS and KPLS methods,the improvements of Q PLS and Q KPLS are as high as 0.4088 A and 0.2752 A,respectively,for the eighth subblock.

The function of the proposed Q-based strategy in saving time and memory costs is especially important for non-linear data-driven regression algorithm.For example,because it only needs to handle an m×m(m is the number of observations)kernel matrix by making use of the so-called “kernel trick”mapping,the time and memory costs of the kernel-based techniques are much more related to the number of observations than to the number of variables[39].Thus the proposed Q-based strategy is promised to remarkably reduce the computation time in model updating procedure for kernel-based algorithms.In our study,in the case of dataset-2(contains830 samples),the computation time of KPLS method is as long as 120 s,while that of Q KPLS algorithm is only 20 s.

Fig.2.The monitoring chart of the second sub-block samples of dataset-2 calculated by the Q PLS algorithm.

4.Conclusions

To improve the performance of the statistical process monitoring system in rubber mixing process,we propose a hardness prediction model using the rheological parameters as predictors.For strongly time-varying properties,a novel Q-based strategy is developed as a universal updating platform for data-driven models.For a model constructed using historical data,support samples with squared prediction errors(or Q statistic)in a pre-optimized range is accumulated over time.Once the number of support samples is sufficiently large,the datadriven model is updated,and then the updated model is used for subsequent process monitoring.Importantly,making good use of the existing Q statistic,the Q-based strategy could integrate the model updating function with the essential process monitoring function of the existing SPM system without dramatic changes.It is there fore practical to the industrial practices.The application of this procedure in a Chinese tire plant demonstrates the superiority of the method.In addition to improve the prediction performance,the time-delay for measurement of hardness can be reduced from about 2–4 h to 2 min.

Fig.3.The prediction RMSE of the Q-based algorithms and corresponding regular algorithms for dataset-1.

Fig.4.The prediction RMSE of the Q-based algorithms and corresponding regular algorithms for dataset-2.

Appendix

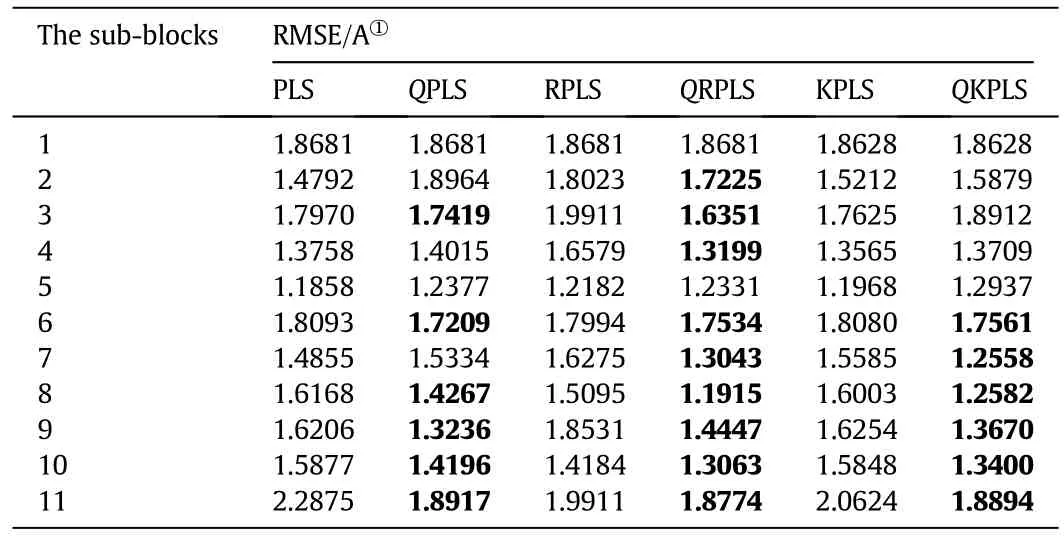
Table A1RMSE values of prediction with Q-based algorithms and corresponding regular algorithms for dataset-1

Table A2RMSE values of prediction with Q-based algorithms and corresponding regular algorithms for dataset-2