Water slip flow in superhydrophobic microtubes within laminar flow region☆

Zhijia Yu*,Xinghua Liu,Guozhu Kuang

Department of Chemical Engineering,Dalian University of Technology,Dalian 116024,China

Keywords:Slip flow Superhydrophobic Microtube Pressure drop Slip length Darcy friction factor

A B S T R A C T The fabrication of superhydrophobic surfaces and the studies on water flow characteristics therein are of great significance to many industrial areas as well as to science and technology development.Experiments were carried out to investigate slip characteristics of water flowing in circular superhydrophobic microtubes within laminar flow region.The superhydrophobic microtubes of stainless steel were fabricated with chemical etching–fluorination treatment.An experimental setup was designed to measure the pressure drop as function of water flow rate.For comparison,superhydrophilic tubes were also tested.Poiseuille number Po was found to be smaller for the superhydrophobic microtubes than that for superhydrophilic ones.The pressure drop reduction rangesfrom 8%to 31%.It decreases with increasing Reynolds number when Re＜900,owing to the transition from Cassie state to Wenzel state.However,it is almost unchanged with further increasing Re after Re＞900.The slip length in superhydrophobic microtubes also exhibits a Reynolds number dependence similarly to the pressure drop reduction.The relation between slip length and Darcy friction factor is theoretically analyzed with consideration of surface roughness effect,which was testified with the experimental results.

1.Introduction

In fluid mechanics,no-slip condition is traditionally considered as the boundary condition for a fluid flowing over a solid surface.However,existing studies show that proper boundary conditions depend on solid–fluid interaction,which is determined by solid surface wettability,material properties of the liquid,shear rate,pressure and surface roughness[1].Experimental measurements indicated that significant slip over some solid surfaces may exist,such as large slip effect at a non wetting fluid–solid interface[2]and the slip flow of complex fluids flowing past solids[3].

The concept of slip boundary condition was first introduced by Navier in 1823.In his model,slip velocity usis proportional to the shear rate at the solid surface[4]:

where λ is the slip length.Slip flow is an important concept because it will result in a significant reduction in pressure drop,which can greatly benefit the application of microfluidic or nanofluidic devices.Slip lengths are generally computed indirectly from pressure drop and flow rate measurements[5–7].Recently,some novel techniques were developed to directly measure flow field in microchannels[8–10]and solid–surface interaction[11,12],so that the slip characteristics can be examined;for instance,rheometry was successfully used by Choi et al.to measure slip length at the scale of microns[13,14].Besides,slip flows were theoretically investigated[15,16]and simulated[17].

Only a few papers reported slip flow on hydrophilic surfaces[18].Existing studies find that slip flows occur more readily on superhydrophobic surfaces,which are characterized by the rough structure on the scale of nm and μm and the low surface energy[19].

It should be noticed that although considerable researches have been devoted to slip flow sin parallel-plateand rectangular microchannels,rather less works related to slippage in circular microtubes have been reported.In fact,laminar flow in a circular tube,namely Hagen–Poiseuille flow,can be considered as the simplest model for many practical flows.It would thus be of great interest to investigate the slip characteristics in round microtubes.Watanabe et al.[20]performed slip flow experiments in highly water repellent tubes of 6–12 mm inner diameter and obtained a correlation between Darcy friction factor and slip length in laminar flow region:

Compared with Eq.(1),(μ/β)can be referred as slip length.Their experimental results agree well with their correlation.

Miniaturization in chemical processing has aroused much attention worldwide.The flow resistance of fluid in microprocessing may be the key factor hindering the commercial application of miniaturization.The investigation on fluid flow in microtubes or microchannels is of great significance especially for finding a method to solve some key problems.In present paper,superhydrophilic and superhydrophobic microtubes were prepared with chemical etching and chemical etching– fluorination treatment.The pressure drop and slip flow characteristics of water flow in a circular superhydrophobic microtube are tested and analyzed by referencing the Darcy friction factor and the slip length for laminar flow in circular microtubes.

2.Experimental

2.1.Description of apparatus

The experimental setup was designed to measure the pressure drop and volumetric flow rate of water through microtubes,as shown in Fig.1.

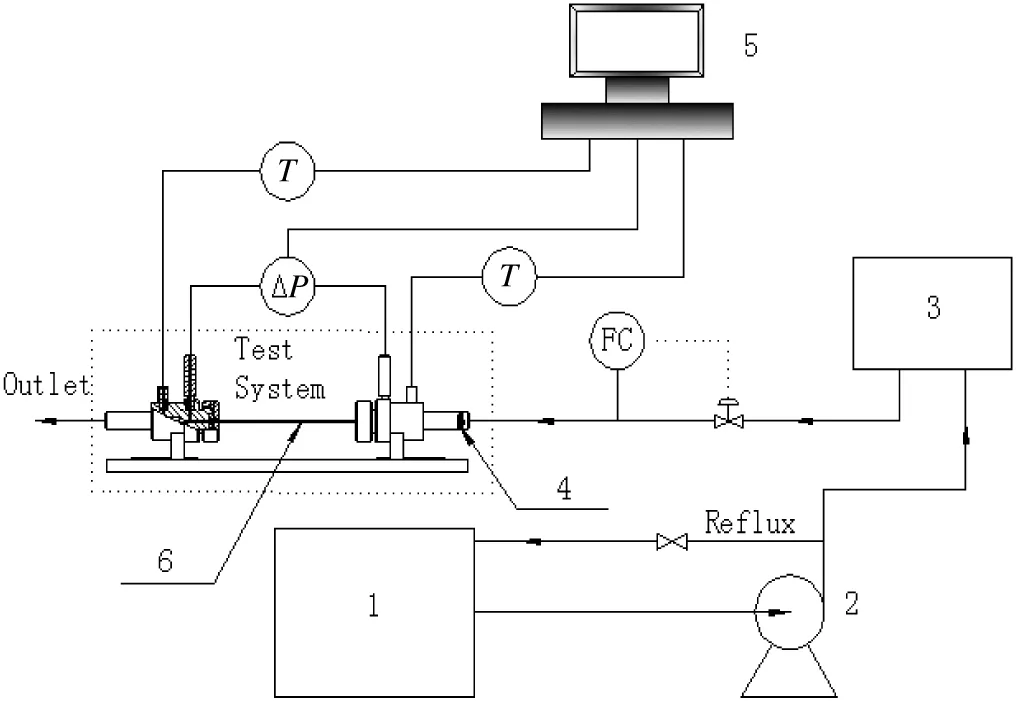
Fig.1.Schematic diagram for experimental system.1—water tank;2—pump;3—buffer tank;4—conjunction;5—data acquisition system;6—micro-tube.

Deionized water is pumped with a centrifugal pump from a water tank into a buffer tank;after flow rate measurement and control it flow s through the test section with a microtube to be tested.The flow diagram is designed with a reflux stream for stable control of water flow rate.The volumetric flow rate of water is measured by a flow-meter which is calibrated by the standard weighing method.The pressure drop is measured by a calibrated pressure drop transducer(model DPST-DP,DPSISN,Shenyang,China).The inlet and outlet temperatures of water are measured with two copperconstantan thermocouples with an accuracy of 0.1°C.Data of temperature and pressure drop are captured via an AD converter.The test tube dimension and roughness are shown in Table 1.Data for tubes after fluorination treatment are the same as those before the treatment,since only a negligible thickness of mono-molecular layer forms by a self-assembly process.

Table 1Parameters of microtubes in the experiments

Darcy friction factor is calculated with

Poiseuille number Po is then obtained as

In this study,Re is less than 1400 and thus the flows are almost in the laminar flow region.

The dimensionless pressure drop reduction Π is defined as

2.2.Fabrication of superhydrophobic microtube

Microtubes of 304 stainless steel,purchased from Fareast Fine Metal,Shenzhen,China,were adopted in the present experiment.Superhydrophilic and superhydrophobic microtubes were prepared with chemical etching and chemical etching– fluorination treatment on the inner wall,respectively,as described below.

Firstly,ethanol and distilled water were used to rinse the microtubes.Then,the microtubew as etched by introducing 25%(by mass)ferric chloride(FeCl3)aqueous solution at room temperature for about 20 min.The etched microtube was rinsed again with distilled water in an ultrasonic w asher.By the abovetreatments,the superhydrophilic microtube was prepared and ready for comparison test.

The superhydrophobic microtube was then prepared by a simple surface fluorination treatment on theinner wall of the superhydrophilic microtube.The fluorination treatment was applied by filling a 1%(by mass)trideca fluorooctyltriethoxysilane(FAS)solution in ethanol at room temperature for about 30 min,forming a self-assembled molecular monolayer on the surface.The samples were baked in an oven at 120°C for about 15 min.The diameter of microtube was measured by cutting the microtube and the diameter of the cross section was measured with a microscope.Five cross sections at different location of the microtube were measured and the average was adopted as the microtube diameter.The maximum uncertainty of diameter is about 10 μm,so that the relevant uncertainty is about 1%–2%.

The wettability was examined by observing the cut microtubes as shown in Fig.2,showing the status of water on the inner wall of the superhydrophilic and superhydrophobic microtubes.Water spreads well on the superhydrophilic wall and the contact angle is about 0°[Fig.2(a)].The water droplets are nearly spherical on the superhydrophobic wall,indicating that the inner wall exhibits excellent water repellency[Fig.2(b)].The advancing and receding contact angles of a water droplet on the superhydrophobic wall were measured to be 158°/140°.The resultant surface morphology was examined by means of scanning electron microscope(SEM,KYKY-2800B),and the result is shown in Fig.3.It can be seen that the surface is configured in a rough structure with plateaus and caves on the scale of microns and nanometers.The roughness was measured to be 4.2 μm by a surface profiler(ET4000AK31,Kosaka Laboratory Ltd.,Japan).

3.Results and Discussions

3.1.Pressure drop

According to the conventional theory,Po should be constant with the value of 64 for fully developed laminar flow in a circular pipe.However,as presented in Fig.4,Po exhibits a Reynolds number dependence for both superhydrophobic and superhydrophilic microtubes used in the experiments.The data in Fig.4 are the averages over 3 microtubes with the same wetting properties.

Fig.2.Pictures of water on the wall of(a)the superhydrophilic microtube,where water appears as spreading water film,and(b)the superhydrophobic microtube,where water appears as almost perfect balls.

Fig.3.Scanning electron microscope(SEM)image of the etched stainless steel surface(3000×).

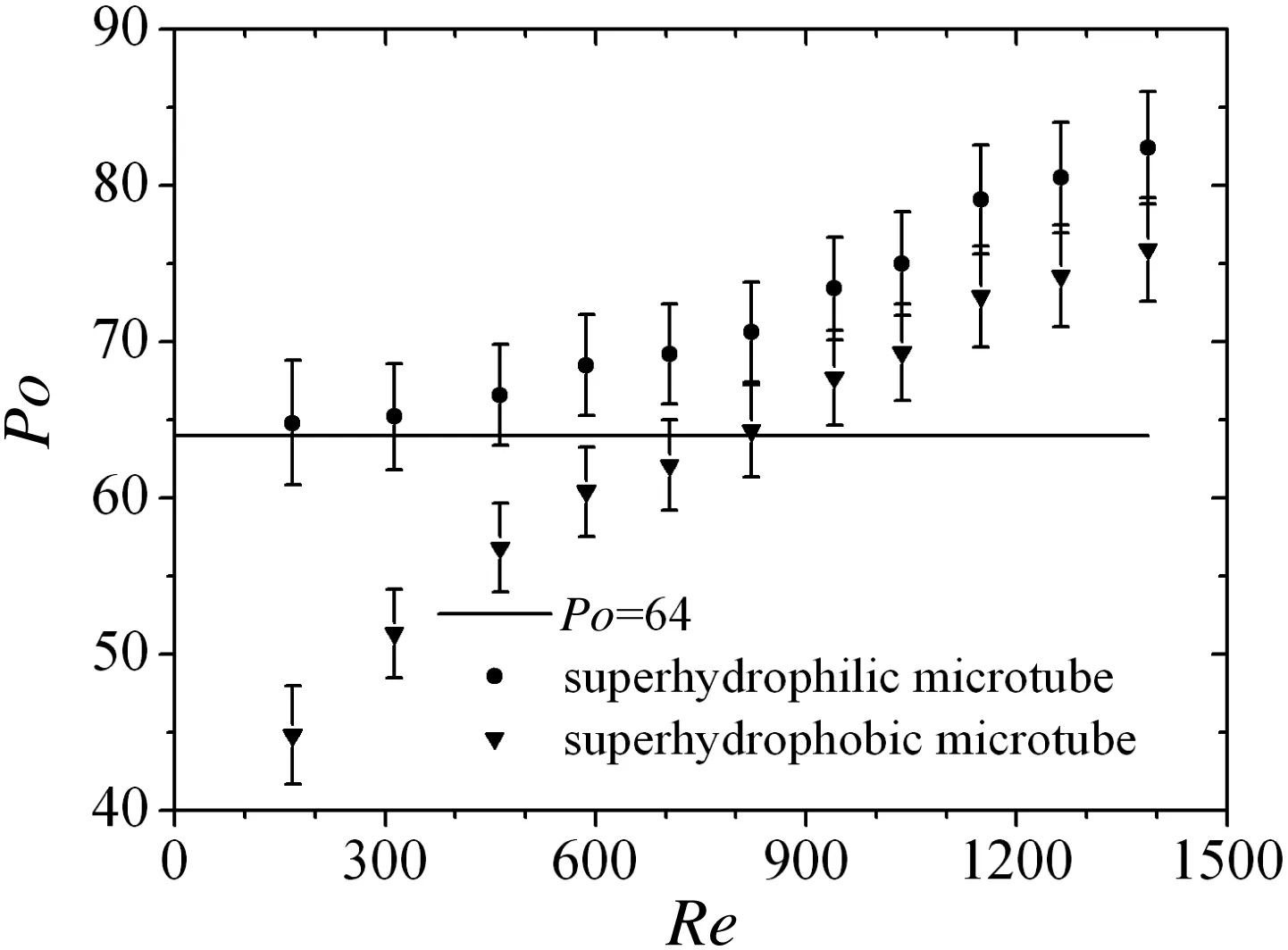
Fig.4.Comparison of Po between the two kinds of microtubes.

For water flowing in a superhydrophilic microtube,Po almost agrees with conventional value when Re is small,but it then becomes larger with increasing Re.This discrepancy is attributed to the effect of relatively great surface roughness and the effect is more pronounced with increasing Re.What's more meaningful presented in Fig.4 is that Po for the superhydrophobic microtube is always smaller than that for the superhydrophilic microtube,indicating obvious reduction in flow friction in the laminar flow region.The drag reduction mechanism is generally attributed to the levitation effect by air-cushion on the superhydrophobic surface[16].For the superhydrophobic microtube used in this experiment,the rough structure on the inner-wall acts as cavities to trap air.It would be difficult for water to enter the cavities due to the low surface energy of the coated FAS.The superhydrophobic surface serves as partly shear-free(air–water)interface,decreasing the pressure drop evidently.How ever,this model is only tenable under low liquid pressure condition w here the Cassie state is prominent.That Po in the superhydrophobic microtube increases with increasing Re is a result of transition from Cassie state to Wenzel state based on Ou's superhydrophobic drag reduction model[3].Although the rough structure(cavities)on the superhydrophobic wall is irregular,we treat a cavity ideally as a truncated cone as represented in Fig.5.Consider that a basic superhydrophobic surface rough structure is a frustum of a cone with a slope angle α and diameter of top hatch dc.Under a pressure difference between water(Pw)and cavity-trapped air(Pa),the water–air interface would have an arc shape(meniscus)forming a contact angle θ.By a simple geometrical calculation and the Laplace–Young equation,the pressure difference of water over cavity-trapped air can be obtained as

Fig.5.Water meniscus at the top of a trapping-air cavity of the superhydrophobic surface.

For present experiment,the water pressure in microtube increases with increasing volumetric flow rate and so Re.The water pressure(gauge pressure)in the superhydrophobic microtube varies from 600 Pa to 8000 Pa with increasing Re.We evaluate ΔP*with Eq.(6),considering that the surface tension of water σ is 0.0727 N·m-1(at 20 °C)and(θ − α)is 100°(e.g.,θ =115°,α =15°).If dc=16 μm,ΔP*w ould be about 3000 Pa,w hile if dc=8 μm,ΔP*w ould be doubled.How ever,it should be noticed that we treated a cavity ideally as a truncated cone.This hypothesis leads great deviation from the real condition.Since most cavities in the superhydrophobic wall are at the scale of microns or even tens of microns and many cavities communicate mutually,an even smaller pressure difference ΔP*results in the penetration of water into some cavities.

It can be seen from Eq.(6)that ΔP*is inversely proportional to the diameter of a cavity.Consequently,gas in bigger cavities is firstly displaced by water with small Re.As Re increases,more cavities are filled with water,resulting in a loss of levitation effect by hydrophobic cavities.That is,the shear free fraction decreases with the increase of Re.Therefore,as shown in Fig.4,Po for the superhydrophobic microtube increases and approaches that for the superhydrophilic microtube with increasing Re while Re＜900.The dimensionless pressure drop reduction Π as a function of Re is shown in Fig.6.Within the operating range,the maximal pressure drop reduction is 31%when Re is small.Π decreases with increasing Re until Re reaches 900.

Fig.6.Dimensionless pressure drop reduction of the superhydrophobic microtube.

Watanabe et al.[20]performed experiments to investigate the flow of water through 6 mm and 12 mm diameter circular pipes with highly water-repellent walls.Drag reduction up to 14%was observed in the laminar flow region while it didn't occur in the turbulent flow region.Although no reason was given in their paper,it is reasonable to suppose that the water pressure is so high in the turbulent flow region that water sags into the micro-cavities on the tube wall.Similar results were observed in the present study.When Re is larger than 900,Po in the superhydrophobic microtube still increases with increasing Re(Fig.4),due to the enhanced effect of the surface roughness.The difference of Po between the two microtubes only changes a little.The dimensionless pressure drop reduction is almost unchanged,with the approximate value of 8%(Fig.7).

Fig.7.The slip length in the superhydrophobic microtube.

3.2.Slip characteristics

From the pressure drop reduction,it is inferred that slip flow occurs in the superhydrophobic microtube.The slip length was calculated to characterize the slip flow.

For a fully developed steady laminar flow in a circular pipe,the Navier–Stokes(N–S)equation for an incompressible Newtonian fluid can be written as

By integrating Eq.(7),with the consideration that(d u/d r)=0 when r=0,we obtain

Substituting Eq.(8)into Eq.(1)gives

w here(−d P/d z)equals(ΔP/L),hence,

In the present study,the slip velocity was evaluated from the difference in volumetric flow rates of water in superhydrophobic microtube(Q2)and that in superhydrophilic microtube(Q1)under the same pressure drop:

Then,the slip length was calculated as

The slip length as a function of Re is shown in Fig.7.It is found that within the operating range,the slip length varies from 5 μm to 63 μm.And the slip length decreases with increasing Re while Re＜900,but then it changes a little with further increasing Re after Re＞900.

Watanabe et al.[20]solved the N–S equation with the slip boundary condition and obtained

where f is Darcy friction factor for laminar flow with fluid slip,and β is the sliding coefficient defined by

Compared with Eq.(1),(μ/β)can be referred to as the slip length.

The applicability of Eq.(2)is based on the classical hydrodynamics that Po=64 for laminar flow in a circular pipe.In this study,the slip length is obtained by referencing the superhydrophilic microtube.Since Po in the superhydrophilic microtube is not a constant value due to the effect of surface roughness,Eq.(2)can not be applied directly in this study.Thus,it is necessary to modify Eq.(2)taking account the surface roughness effect.Mala&Li[21]experimentally and theoretically investigated the flow characteristics in microchannels.They proposed a roughness-viscosity model to account for the effect of surface roughness on the flow friction.In the model,the effective liquid viscosity was expressed as(μ+ μR).The increased viscosity enhances the momentum transfer and thus increases the flow friction.

Inspired by that investigation,we also introduced the roughnessviscosity μRto account for the surface roughness effect.Besides,we defined an effective Reynolds number Reeffby the following equation:

Thus,the roughness-viscosity μRcan be calculated by:

After introducing the roughness-viscosity μR,Eq.(8)becomes

By integrating Eq.(16),and ow ing to the boundary condition that u=0 at r=R,velocity profile under the no-slip boundary condition is obtained:

Combining Eqs.(10)and(17)yields the velocity profile under the slip boundary condition:

The volumetric flow rate is

Then the average velocity in the cross section of a tube can be evaluated as

Therefore,the friction factor for laminar flow with the slip boundary condition,fscan be expressed as

The relation between Re and Reeffis

Thus,Eq.(21)can be further expressed as

The old Fairy thought so too, but as this was not at all what she wished, she took care to throw such an enchantment25 over the Princess that she appeared to Featherhead quite ugly and awkward, though to every one else she looked just as usual

It can be seen that,when the slip length is obtained by referencing a superhydrophilic microtube with non-negligible surface roughness,the friction factor depends on Re,the dimensionless parameter(λ/R)and also the roughness-viscosity.If the superhydrophilic surface is smooth,Eq.(23)would be equal to Eq.(2)on substituting μR=0 into the equation.

Furthermore,substituting Eq.(14)into Eq.(21),we obtain

Substituting the values of the slip length,the roughness-viscosity and the superhydrophilic microtube friction factor into Eq.(24),we obtained the calculated value of friction factor fs.Then,we compared fswith the experimental values and Watanabe's model predicted values(i.e.,Eq.(2))in Fig.8.It can be seen that Watanabe's model can predict the friction factor well in small Re range,but under predicts in higher Re.How ever,the agreement between the experimental values and the calculated values with Eq.(24)is better,indicating the influence of μRon Darcy friction factor.The roughnessviscosity μR,calculated with Eq.(15),varies as function of Re as shown in Fig.9 for a microtube with inner diameter of 0.55 mm.It can be seen that the roughness-viscosity is small at low Re,but increases quickly after 900,contributing the more evident effect on friction factor.

Fig.8.Comparison of friction factor between the experimental values,Eq.(24)calculated values and Watanabe's model predicted values.

Fig.9.The roughness-viscosity μR varies with Re for a microtube with inner diameter of 0.55 mm.

4.Conclusions

Superhydrophobic stainless steel microtubes were fabricated with chemical etching and fluorination treatment.The contact angle of a water droplet on the superhydrophobic wall reaches 158°.Investigations on drag reduction and slip flow are carried out in the laminar flow region in circular superhydrophobic microtubes.The results show that Po for the superhydrophobic microtube is smaller than that for the superhydrophilic microtube.When Re＜900,the dimensionless pressure drop reduction in the superhydrophobic microtube decreases as Re increases,with the maximal drag reduction up to 31%.It then reaches a relative stable value of 8%after Re＞900.The slip length in the superhydrophobic microtube varies from 5 μm to 63 μm.It also exhibits a Reynolds number dependence similarly to the pressure drop reduction.A roughness-viscosity to take account of the surface roughness effect is introduced,and the Navier–Stokes equation is solved with the slip boundary condition.A relationship between Darcy friction factor and the slip length is developed with the modification of roughness-viscosity as

The predicted values exhibit an excellent agreement with the experimental results.

Nomenclature

d inner-diameter of a microtube,m

fsDarcy friction factor for laminar flow with the slip boundary condition

L length of microtube,m

P pressure,Pa

Po Poiseuille number(Po=f Re)

ΔP pressure drop between entrance and exit of a microtube,Pa

ΔP* pressure difference of water over cavity-trapped air,Pa

Q water flow rate,m3·h−1

Re Reynolds number(Re= ρdu/μ)

Reeffeffective Reynolds number

R radius of a tube,m

r radial coordinate,m

u velocity,m·s−1

usslip velocity,m·s−1

w width of a micro-gap

β slip coefficient,kJ·(m3·s)-1

θ apparent water contact angle(WCA),(°)

λ slip length,m

μ liquid dynamic viscosity,Pa·s

μRroughness-viscosity,Pa·s

Π dimensionless pressure drop reduction

ρ density of water,kg·m3

σ surface tension of fl uid,N·m−1

Subscripts

1 for superhydrophilic microtube

2 for superhydrophobic microtube