基于马尔可夫链的飞机结构腐蚀状态预测

王志平,马旻昱,张春晓,苏景新

(中国民航大学 天津市民用航空器适航与维修重点实验室，天津 300300)

基于马尔可夫链的飞机结构腐蚀状态预测

王志平,马旻昱,张春晓,苏景新

(中国民航大学 天津市民用航空器适航与维修重点实验室，天津 300300)

腐蚀损伤是最常见的飞机结构损伤形式之一，会降低结构的剩余强度和耐久性。针对在役民用典型机型飞机易腐蚀结构，首先将腐蚀状态划分为5个等级；其次拟合遭受腐蚀的飞机结构剩余厚度递减函数，给出腐蚀状态转移概率矩阵，建立马尔可夫状态预测模型。最后收集某型飞机后货舱隔框腐蚀数据作为算例，预测了隔框结构在潜伏期之后的腐蚀状态。结果发现使用26个月之后，沿海地区飞机隔框结构腐蚀已达到三级状态。预测结果与工程实践相符，说明马尔可夫模型适用于飞机结构腐蚀状态预测。

飞机结构；腐蚀；马尔可夫模型；状态预测

腐蚀损伤是最常见的飞机结构损伤形式之一。严重的结构腐蚀不但直接影响飞机的飞行安全，降低飞机的服役期限[1],还会加重机务维修工作负担，带来高额的维修费用。因此，针对在役民用典型机型飞机易腐蚀结构，探索腐蚀检修数据的规律，进行飞机结构腐蚀退化性能预测，对减少腐蚀带来的经济损失、确保飞机结构的安全运行有着重要的工程实践意义。

目前，国内外关于飞机结构腐蚀的研究主要集中在飞机主体材料的腐蚀损伤原理与检测、腐蚀防护与修复方面[2-7]，而基于民航在役飞机的腐蚀数据，对飞机结构性能腐蚀退化预测的研究相对较少。如张腾等人[8]提出了通过预腐蚀疲劳试验确定飞机结构寿命包线的腐蚀影响系数法，建立了典型服役环境中飞机金属结构腐蚀疲劳关键件的剩余寿命预测方法。

从作者掌握的文献来看，现有理论模型未充分考虑腐蚀维修工程实践的时变性和样本采集的局限性，使得模型参数带有很大的不确定性，难以满足结构腐蚀预测和可靠性动态管理的要求。马尔可夫理论能够很好地处理变量的随机变化过程并进行动态预测，在道路、桥梁、管道劣化模型方面都有成功应用的案例[9-11]。Provan和Rodriguez[12]最先使用非均匀马尔可夫过程模拟腐蚀坑深度的发展，Hong[13]等人利用马尔可夫过程模拟了点蚀的增长阶段。因此，本工作采用马尔可夫理论进行飞机结构腐蚀状态的预测研究。

1　飞机结构腐蚀状态

马尔可夫过程[14-16]是具有无后效性的随机过程。后效性是指系统未来所处的状态只与现在系统状态有关,而与系统过去的状态无关。通过对某航空公司飞机结构腐蚀检测数据分析可知：飞机结构腐蚀是动态系统的状态转移过程，该过程具有随机性；飞机结构未来的腐蚀状态只与系统所处的腐蚀状态有关，而与过去的腐蚀状态无关。可见飞机结构腐蚀具有马尔科夫性。并且飞机结构腐蚀状态间的转移概率仅与腐蚀状态有关，而与时刻n无关，因此将飞机结构腐蚀看作齐次马尔可夫链。

结构腐蚀状态可以用多种特征量来表示，例如腐蚀深度、面积、体积等。由于本工作研究的飞机结构腐蚀形态以点蚀为主，所以选取腐蚀深度作为度量腐蚀损伤的代表值[17-18]。航空器结构持续完整性大纲[19-20]通过不影响结构件极限设计强度可以除去的腐蚀最大量(通常指材料厚度)将飞机结构腐蚀划分为三个等级，即1级腐蚀、2级腐蚀、3级腐蚀。根据民航飞机结构维修的施工惯例，对不同程度的腐蚀损伤采取的维修措施又有区别，因此可进一步将三个等级的结构腐蚀划分为5个状态，即腐蚀状态空间S={1，2，3，4，5}，如表1所示。

表1　腐蚀深度的状态划分Tab. 1　Corrosion states divided by maintenance measurements

2　马尔可夫预测模型

飞机不同结构的极限强度不同，而且腐蚀环境也存在差异，因此需针对不同结构，不同站位的结构腐蚀数据分别进行腐蚀深度预测。本工作在对飞机结构腐蚀状况进行预测时，主要是基于收集到的剩余厚度数据(剩余厚度等于原厚度与腐蚀深度的差值)建立飞机结构腐蚀状况预测模型。

2.1飞机结构剩余厚度递减模型

依据飞机维修时得到的腐蚀数据确定腐蚀发展趋势及状态分布建立马尔可夫预测模型，但是在实际腐蚀检测过程中，缺乏充分的检测数据，需要通过检测得到的数据近似拟合出飞机结构剩余厚度的降低趋势线。飞机结构腐蚀属于电化学腐蚀[19]，初始阶段腐蚀速率较快，腐蚀速率随着时间逐渐减慢，因而可假设剩余厚度按以下指数形式发展[20]：

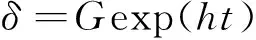
(1)

式中:G,h均为系数;t为前一次维修到本次维修的间隔时间(month);δ为剩余厚度(mm)。根据飞机维修得到的腐蚀数据，利用最小二乘法，拟合成式(1)指数函数形式，分析剩余厚度的发展趋势，确定结构腐蚀状态。

2.2状态转移矩阵

这里将飞机结构腐蚀状态划分为5个状态，则转移概率矩阵P的一般形式为：

(2)

式中，转移概率值Pmn反映腐蚀程度从状态1一直到状态5的变化过程。假设飞机结构腐蚀不采取防腐措施，随着服役时间的增长，最大腐蚀深度将越来越大，其腐蚀状态等级保持不变或变差。当腐蚀状态达到5时，便不能转移到其他状态，停留在此状态。此时转移概率矩阵P的形式为：

(3)

通过公式(1)，求解各时间间隔t(1,2,…,ti…,tn)下的剩余厚度，并按照表1确定腐蚀状态。当时间间隔为tn时，腐蚀状态从4变为5，此时腐蚀状态将一直停留在状态5，表明飞机结构腐蚀状态已达到最严重状态，终止时间t的取值。从而得到一系列随时间变化的腐蚀状态数据。利用统计分析法计算飞机结构腐蚀系统在ti时由状态i到状态j的转移概率值Pij，计算过程如下：①统计飞机结构腐蚀状态为i的次数gi；②计算出处经过一步转移从状态i到状态j的次数gij，则Pij的计算公式如下：

(3)

进而求出转移概率矩阵P，反映出从开始腐蚀到五级腐蚀的变化规律。

2.3腐蚀状态预测模型

应用马尔可夫链对飞机某结构腐蚀剩余厚度进行预测时，需要确定剩余厚度的初始状态和转移概率矩阵。将最后一次检测得到的剩余厚度作为初始状态，用向量K=[K1,K2,K3,K4,K5]表示，其中K1,…,K5为结构腐蚀状况在各个状态的概率值，范围为[0,1]。当初始状态K和转移概率矩阵P确定后，根据齐次马尔可夫链性质，在最后一次检测之后第m次(m≥1)检测时的腐蚀状态分布预测值为：

(5)

3　计算实例

3.1确定飞机结构腐蚀状态

利用以上模型对沿海地区某型飞机后货舱767站位隔框腐蚀深度进行预测。一般需要使用同一架飞机结构件在不同时间测得的结构腐蚀数据。但是在对飞机结构的例行维护和检查中，一旦发现腐蚀损伤，会立即进行修理(即去除腐蚀层，并恢复结构强度和防护层)，因此很难在同架飞机上得到同一位置的腐蚀深度的连续发展数据。本工作使用的飞机结构件腐蚀数据取自同一个服役机场的同一机型飞机，且腐蚀构件的材料、加工工艺、防护体系相同，将这些测量到的腐蚀损伤数据作为一个母体来考虑，亦可以得到飞机在不同服役时间状态下的腐蚀深度的连续发展数据。算例中采用的数据如表2所示，数据来自某机场同一型号飞机后货舱区域的767站位隔框，腐蚀发展时间为距离上次维护检查的时间(即维护间隔)。

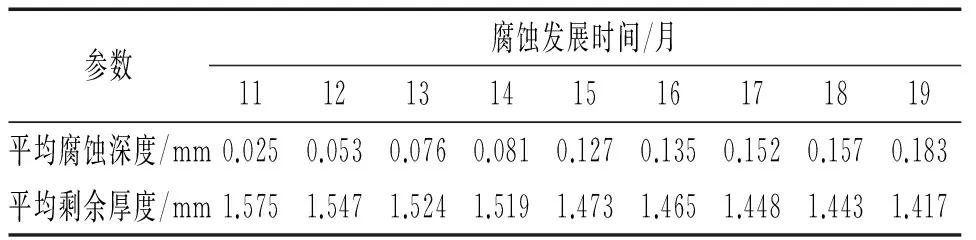
表2　某型飞机767站位隔框在不同腐蚀发展时间 的腐蚀数据Tab. 2　Corrosion data of 767 aft cargo frame at different corrosion time

根据表2中时间和剩余厚度数据，通过最小二乘法，运用SPSS进行曲线拟合，拟合成公式(1)的指数函数形式。拟合结果如图1所示。

图1　指数函数拟合效果图Fig. 1　Fitting effect chart of exponential function

由表3可知拟合函数的拟合优度R2接近于1，说明拟合效果很好，而且该递减模型的显著性检验(F检验)P值小于0.05，进一步说明拟合的模型显著，该模型可用作飞机结构剩余厚度递减模型，因此剩余厚度随时间发展的函数关系式为：

(6)

表3　拟合函数的检验结果及参数Tab. 3　Test results and parameters of fitting function

已知隔框结构的原始厚度为1.6 mm，根据飞机结构中隔框的极限强度[21]进行腐蚀状态划分，如表4所示。

表4　隔框腐蚀状态划分Tab. 4　Corrosion states of frame divided into 5 levels by corrosion depth

表4中划分了隔框腐蚀状态，由表2可知最后一次维修的间隔时间为19个月，最大腐蚀深度为0.183 mm，腐蚀状态为3，则初始状态为K=[0,0,1,0,0]。

从检测到腐蚀深度开始对时间进行取值，带入公式(6)，计算剩余厚度，得到腐蚀状态变化情况，如表5所示。

表5　不同腐蚀发展时间的腐蚀数据及对应状态Tab. 5　Corrosion data and corresponding states at different corrosion times

3.2确定腐蚀状态转移矩阵

依据表5中的飞机结构腐蚀数据及其对应状态，统计处于各腐蚀状态的次数gi和腐蚀状态之间的转移次数gij，根据公式(4)求解转移概率矩阵中各状态转移概率的值Pij，得到转移概率矩阵P：

(7)

3.3腐蚀状态预测及验证

根据公式(5)进行马尔可夫链进行预测，由第19个月的腐蚀状态开始，运用MATLAB计算得到腐蚀状态分布的预测值，如表6所示。

通过对表6中数据进行分析可知，飞机后货舱隔框腐蚀状态在26个月的状态向量K26=[0，0，0.133 5，0.381 2，0.485 4]，其中状态5的概率值最大，为0.485 4。可见飞机后货舱隔框腐蚀状态最可能进入状态5，达到三级腐蚀，因此需要报告并进行隔框更换。

表6　腐蚀状态的概率值在不同腐蚀发展时间的 预测结果Tab. 6　Predictive results of probability values of corrosion states at different corrosion times

以第12个月的腐蚀状态为初始状态，运用MATLAB计算得到13个月到19个月的飞机后货舱隔框腐蚀状态马尔可夫预测值，与13个月到19个月的实际数据对比以验证马尔可夫模型准确性。如表7所示。

表7　马尔可夫模型的验证结果Tab. 7　Verification results of Markov modeling

通过与实际腐蚀深度状态变化进行对比，发现利用马尔可夫链预测的结果与实际状态变化基本一致，说明马尔可夫链适用于腐蚀条件下飞机结构性能退化预测。

4　结论

基于飞机结构腐蚀的基本原理，通过恰当方法选择腐蚀数据，应用马尔可夫链对飞机结构腐蚀状态进行预测。通过计算实例，发现运用马尔可夫链预测与实际情况基本符合，表明马尔可夫链可应用于飞机结构腐蚀状态预测。主要结论如下：

(1) 某沿海地区典型机型后货舱隔框在腐蚀环境下的剩余厚度递减函数关系式为δ=1.818 exp(-0.013t)。

(2) 该机型飞机后货舱隔框在沿海地区在26个月进入腐蚀状态5，达到三级腐蚀。

(3) 以第11个月的飞机结构腐蚀为初始状态，对12到19个月的结构腐蚀状态进行预测，发现与实际情况基本一致。

因此,应用马尔可夫链进行飞机结构腐蚀状态预测是合理可行的。

[1]张有宏,吕国志,李仲,等. 铝合金结构腐蚀疲劳裂纹扩展与剩余强度研究[J]. 航空学报,2007,2(28):332-335.

[2]JONES K,DAVID W H. Prior corrosion and fatigue of 2024-T3 aluminum alloy[J]. Corrosion science,2006,48(10):3109-3122.

[3]RUSSO S,SHARP P K,MILLS T B,et al. The influence of the environment and corrosion on the structural integrity of aircraft materials[J]. Fatigue and Fracture of Engineering Materials and Structures,2009,32(6):464-472.

[4]贺崇武,蔡新锁,李素强. 飞机典型连接件腐蚀及腐蚀疲劳试验研究[J]. 腐蚀与防护,2006,27(3):118-121.

[5]陈群志,孙诈东,陆维忠,等. SEBF/SLF重腐蚀防护涂层应用于典型飞机结构中防腐性能综合评定[J]. 中国腐蚀与防护学报,2005,25(6):365-368.

[6]张蕾,刘慧丛,朱立群,等. 局部修复对典型环境中飞机外部结构件腐蚀的影响及腐蚀当量关系修正[J]. 腐蚀与防护,2014,35(8):833-837.

[7]耿德平,宋庆功. 航空材料腐蚀疲劳研究进展[J]. 腐蚀与防护,2011,32(3):206-209.

[8]张腾,何宇廷,张海威,等. 基于寿命包线的飞机金属结构寿命预测方法[J]. 南京航空航天大学学报,2014,46(3):413-418.

[9]袁赓,王树刚,黄一. 基于马尔可夫链的埋地燃气钢管管壁腐蚀预测[J]. 哈尔滨工业大学学报,2010,42(8):1328-1331.

[10]吴明亮,郝点,刘锦昆. 基于灰色马尔可夫理论的油气管道腐蚀剩余寿命预测[J]. 管道技术与设备,2008(5):43-45.

[11]CALEYO F,VELZQUEZ J C,VALOR A,et al. Markov chain modelling of pitting corrosion in underground pipelines[J]. Corrosion Science,2009,51(9):2197-2207.

[12]PROVAN J W,RODRIGUEZ E S. Development of a Markov description of pitting corrosion[J]. Corrosion,1989,45(3):178-192.

[13]HONG H P. Inspection and maintenance planning of pipeline under external corrosion considering generation of new defects[J]. Structural Safety,1999,21(3):203-222.

[14]胡迪鹤. 随机环境中的马尔可夫过程[M]. 北京:高等教育出版社,2011.

[15]钱卫东,刘志强. 基于灰色马尔可夫的道路交通事故预测[J]. 中国安全科学学报,2008,18(3):33-36.

[16]王永刚,吕学梅. 民航事故征候的灰色马尔可夫预测[J]. 安全与环境学报,2008,8(1):163-165.

[17]AC-121-65航空器结构持续完整性大纲[S].

[18]陈跃良,杨晓华,秦海勤. 飞机结构腐蚀损伤分布规律研究[J]. 材料科学与工程,2002,20(3):378-380.

[19]穆志韬,熊玉平. 高强度铝合金的腐蚀损伤分布规律研究[J]. 机械工程材料,2002,26(4):14-16.

[20]苏维国,穆志韬. 基于损伤检测的腐蚀疲劳寿命预测概率模型[J]. 装备环境工程,2009,6(5):33-38.

[21]张行,田秀云,翟月英,等. 飞机结构修理中的极限强度分析方法[J]. 中国民航学院学报,1986(1):1-8.

Application of Markov Chain to Prediction of Corrosion Conditions for Aircraft Structures

WANG Zhi-ping, MA Min-yu, ZHANG Chun-xiao, SU Jing-xin

(Tianjin Key Laboratory for Civil Aircraft Airworthiness and Maintenance, Civil Avation Unversity of China,Tianjin 300300, China)

The corrosion damage is one of the most common injuries in aircraft structures, which reduces the residual strength and durability of aircraft structures. Therefore, this study focused on the prediction of corrosion states of a typical civil aircraft structure based on Markov theory. Firstly, the corrosion states were divided into five levels. Secondly, the decreasing function of remaining thickness of corroded structures were fitted. The corrosion state transition probability matrix was calculated, and the corrosion depth of Markov predictive models was given. The corrosion states of aft cargo frame in the typical civil aircraft were adopted in the example. The corrosion state of the frame at the time after incubation period was predicted, and the result indicated that the frame corroded into the most serious state at coastal site after 26 months. The prediction of Markov model is conformed to the engineering practice, indicating that Markov model is applicable to the prediction of aircraft structural corrosion state.

aircraft structure; corrosion; Markov modeling; state prediction

10.11973/fsyfh-201510009

2014-10-15

国家自然科学基金(21303261); 中央高校基本科研业务费中国民航大学专项(3122013D004); 天津市民用航空器适航与维修重点实验室开放课题

王志平(1963-)，教授，博士，从事材料表面改性研究，022-24092074，zpwang@cauc.edu.cn

TG174; V215.5

A

1005-748X(2015)10-0942-05