RB位移模式挡土墙非极限状态被动土压力研究
丰巨武 周慧珍
(1.太原理工大学水利科学与工程学院 山西太原 030024;2.山西省水利水电勘测设计研究院 山西太原 030024;3.太原理工大学图书馆 山西太原 030024)
挡土墙土压力问题是岩土力学中的重要分支,一直受到工程界的高度关注。在重力式挡土墙挤压回填土体时,形成被动土压力。墙体挤压填土的方式有平移挤压(T模式)、绕墙底转动挤压(RB模式)、绕墙顶转动挤压(RT模式)三种典型形式和混合挤压。墙体位移量达到一特定值就形成极限状态被动土压力,墙体位移量小于此特定值对应的土压力为非极限状态被动土压力。实际工程中的被动土压力绝大多数为非极限状态被动土压力。本文就绕墙底转动挤压(RB模式)挡土墙、非极限状态土压力进行探讨。
1 计算模型
对于RB模式非极限状态被动土压力的情况,墙体挤压回填土体时,墙后土体具有被挤出的趋势,假定墙后填土存在滑移面——准滑移面和准滑动土楔,如图1(a)所示。根据水平层分析法[1],在埋深y处取水平微元进行力的分析,挡土墙转动时,相邻水平微元之间存在相互摩擦而形成层间剪应力,单元两侧与墙背及稳定土体存在摩擦力。这些剪切摩擦使得墙后垂直土压力和水平土压力发生较大变化。
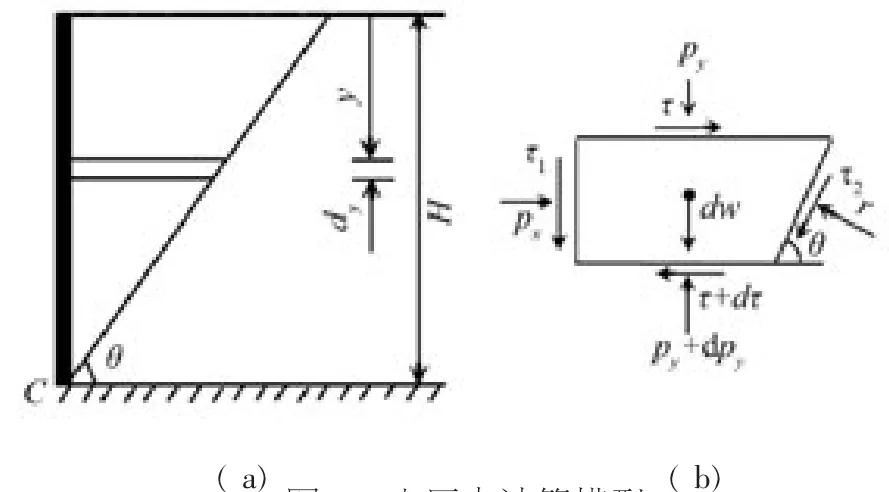
图1 土压力计算模型
墙后填土没有达到极限状态,其填土的内摩擦角没能全部发挥[2],令内摩擦角的发挥值为φm,其大小与墙体位移有关;同理,墙、土外摩擦角的发挥值δm与墙体位移也相关。 φm、δm的取值[3]见式(1)和式(2)。 墙体转动时,墙背各计算点的水平位移不同,墙后不同高度的土体内摩擦角、墙土外摩擦角发挥值不同。

式中:φ0、δ0──填土初始内摩擦角、墙土初始外摩擦角;
φ、δ──完全发挥的内、外摩擦角(内、外摩擦角最大值);
Kd──墙体位移对 φm和 δm影响的系数,Kd=4arctan( S/SC)/π。 S 为墙背各计算点水平位移量,SC为内、外摩擦角达到最大值时所需的墙体水平位移量。φ0的计算可采用改进的库仑方程式[4]求得:

式中,K0是静止侧压力系数,对于正常固结土,K0=1-sinφ;δ0可按通常取值的方法保守取为φ0/2。
据库仑土压力理论,准破裂面倾角θ的计算公式为:

相邻水平层之间的层间摩擦角[6]φ′m=(0.4-0.7)φ,其值变化不大,本文取φ′m=0.5φ。墙背各计算点的被动土压力系数取库仑被动土压力系数,如式(5),墙背各计算点位移不同,摩擦角发挥(取值)不同,对应的土压力系数随之变化。

2 土压力公式推演
在图1中,令

根据图1(b)水平方向受力平衡可得:

简化整理得

根据竖直方向受力平衡可得:
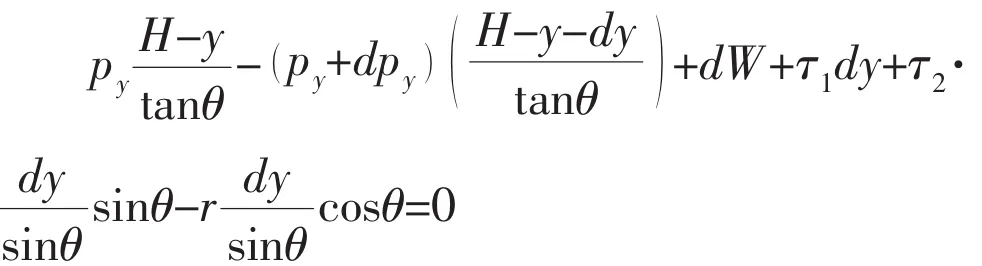
整理可得

由式(6)~(8)得RB模式被动土压力求解的基本方程:

其中

式中:γ为土体容重;y为水平微分单元距墙顶距离;H为墙高。
方程(9)的解为

上式满足边界条件:y=0时,py= 0的特解

墙后被动土压力分布
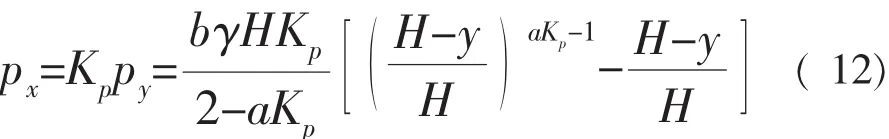
3 土压力分析
选取参考文献[7]中模型试验参数:挡土墙高度H=1m,砂土重度γ=15.5kN/m3,填土内摩擦角φ=34.9°,墙土间外摩擦角 δ=23°,由式(3)试算可得 φ0=20.7°,取 δ0=10.35°。 利用本文公式,取不同 S0/Sc值( S0为墙体转动时,墙顶的水平位移量),可求得挡土墙被动土压力分布、合力及其作用点高度,绘制图2~图4。
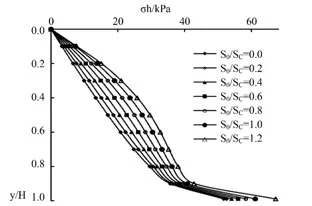
图2 位移对土压力分布的影响
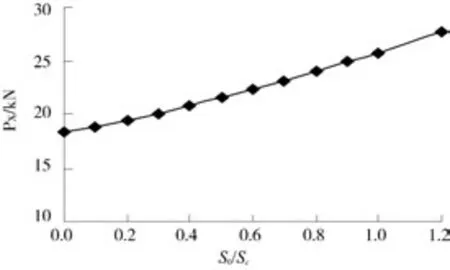
图3 位移对合力的影响
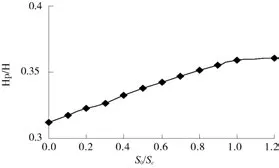
图4 位移对水平合力作用点影响
RB位移模式、挡土墙轻度挤压填土情况下,被动土压力近似折线分布。在上直线段,计算点从墙顶下移过程中,位移逐渐减小,填土摩擦角发挥减少,土压力系数随之减小;但在此过程中,墙背和稳定土体给予准滑动土楔较多的向下摩擦力,垂直土压力增大较多,水平土压力呈增大趋势。土压力分布的下直线段处于墙踵附近,准滑动土楔宽度不断减小,墙背和稳定土体给予准滑动土楔的向下摩擦力占垂直总土压力的比重大幅度增加,水平土压力急剧增大;随S0/Sc增大,在墙顶附近的区域,计算点的水平位移大,土压力系数增值较多,上直线段由近似直线变化为微凸曲线,下直线段变化不大。
S0/Sc增大,墙体挤压填土程度增强,墙后土体的摩擦角整体发挥多,水平的土压力合力加大,在计算范围内,水平合力近似直线增加,见图3。S0/Sc增大时,墙顶附近区域摩擦角发挥多,土压力增大较快,水平合力作用点抬高,合力作用点到墙底的距离为(0.31~0.36)H。S0/Sc>1.0之后,合力作用点抬高的速率减缓,见图4。理论计算值与实验值[8]的相对差见表1,S0/Sc=0.3、0.6、1.0三个位移的水平合力相对差分别为2.73%、2.68%和17.13%,平均相对差值7.51%。
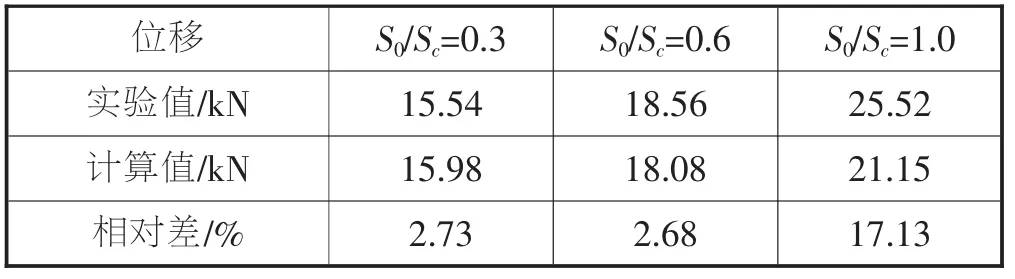
表1 计算值与实验值比较
4 结论
RB位移模式挡土墙非极限状态被动土压力近似呈双折线分布,在墙踵附近的土压力增长幅度加快。在S0/Sc≤1.2范围,非极限状态被动土压力合力线性增大,合力作用点到墙底的距离为(0.31~0.36)倍墙高,随S0/Sc增大,作用点上升,但上升幅度逐渐减缓。
[1]王元战,李 蔚,黄长虹.墙体绕基础转动情况下挡土墙主动土压力分布[J].岩土工程学报,2003,25(2) :208-211.
[2]Ichihara,M.andmatsuzawa,H.Application ofplanestrain test to earth pressure[C].Proceedings of the 8`h ICSMFE,1973,Vol.1.:185-190.
[3]徐日庆,龚 慈,魏 纲等.考虑平动位移效应的刚性挡土墙土压力理论[J]. 浙江大学学报 ( 工学版),2005,39(1):119-122.DOI:10.3785/j.issn.1008-973X.2005.01.022.
[4]蒋 波,应宏伟,谢康和等.平动模式下挡土墙非极限状态主动土 压力计 算 [J]. 中国公 路学 报,2005,18(2):24-27.DOI:10.3321/j.issn:1001-7372.2005.02.005.
[5]卢坤林,朱大勇,杨 杨等.位移及拱效应下的计算方法[M].1版.北京:国防工业出版社.2012.26-27.
[6]CHANGm FLateral earth pressure behind rotating walls[J].Canadiangeotechnical Journa,1997,34( 4);498-509.
[7]卢坤林,朱大勇,杨 杨等.位移及拱效应下的计算方法[M].1版.北京:国防工业出版社.2012.113-115.
[8]徐日庆,陈叶开,杨仲轩等.刚性挡土墙被动土压力模型试验研究[J].岩土工程学报,2002,24( 5):569-575.

