一种基于时域混合的DWT-SVD盲数字水印算法

张凤娟，李琦，高军萍，秦丽伟

（河北工业大学信息工程学院，天津300401）

一种基于时域混合的DWT-SVD盲数字水印算法

张凤娟，李琦，高军萍，秦丽伟

（河北工业大学信息工程学院，天津300401）

提出了一种基于时域混合的盲数字水印新算法。该算法一改传统水印的嵌入过程，首先对载体图像进行分块，利用最佳信号与载体图像进行时域混合以改变图像信息的分布，之后通过离散小波变换结合奇异值分解完成水印嵌入，再进行时域混合恢复得到嵌入水印的图像。进行各种攻击测试，并与传统DWT-SVD数字水印算法进行比较。实验结果表明，时域混合算法具有很好的隐蔽性和鲁棒性。

数字水印；时域混合；最佳信号；小波变换；奇异值分解

自进入信息化时代后，数字媒体的大量流通和复制使安全和版权问题日益突出。数字水印是将版权信息隐性嵌入数字媒体，从而起到保护数字媒体和隐秘通信的作用，得到广泛应用。

常规水印算法的研究关注算法抵抗一般攻击的能力、隐藏水印信息量的多少等因素［1］。因时域水印具有隐蔽性差的特点，目前主要针对变换域进行展开，经常使用的变换域算法包括DCT、DWT以及Fourier-Mellin等［2］。在算法鲁棒性方面，自90年代开始，信息与通信理论特别是扩频通信理论的研究不断完善，进一步提高了水印算法的鲁棒性［3］。最近，有学者应用矢量量化［4］技术，可以提高抵抗一般攻击的能力。目前，许多鲁棒水印算法采用奇异值分解方法［5］。鉴于奇异值的稳定性，实验验证此类算法的鲁棒性较好。现有的数字水印优化问题，基本都是在水印嵌入之前对水印图像进行置乱、扩频等操作，然后完成嵌入。

针对水印优化问题，提出一种新的设计思想，即载体图像时域混合。算法基本思路为：在水印嵌入前，选择具有良好相关特性的最佳信号对载体图像进行时域混合；然后，应用离散小波变换结合奇异值分解SVD完成水印信息嵌入。研究结果表明，采用最佳信号对载体图像进行时域混合处理，可以进一步提高水印的隐蔽性，并具有较好的鲁棒性。

1　相关理论

1.1最佳信号

最佳信号并没有严格的数学定义，不同工程应用领域要求不尽相同。大体而言，具有良好相关特性的信号均可称为最佳信号［6］。对最佳信号还有如下要求［6］：良好的随机性、长周期、较高的线性复杂度、平衡性好。在最佳信号设计理论中，最佳二进阵列是一种典型的信号形式。

定义1设X=［x（s1，s2，…，sn）］和Y=［y（s1，s2，…，sn）］为两个n维N1×N2×…×Nn阶阵列，其中0≤si≤Ni-1，1≤i≤n，则阵列X和Y的循环互相关函数为：

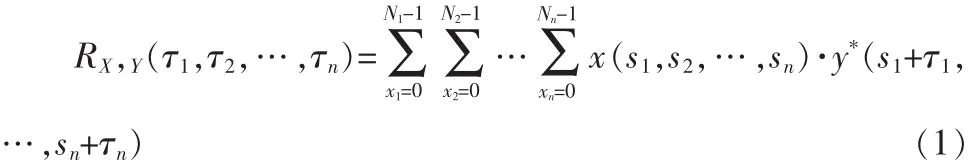
上式中，si+τi=（si+τi）modNi，上标*表示复共轭。若X=Y，则称RX，X（τ1，τ2，…，τn）为阵列X的循环自相关函数，简称为阵列X的自相关函数。若阵列中的元素取值为±1，那么该阵列成为二进阵列。

若二进阵列X的自相关函数满足：

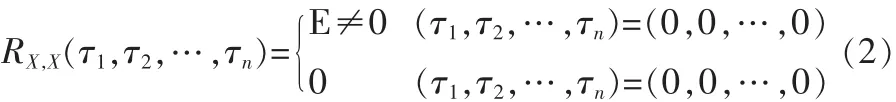
则称阵列X为n维N1×N2×…×Nn阶最佳二进阵列。一维最佳二进阵列称为最佳二进序列。

通过对雷达、声纳、码分多址等系统中信号检测过程的研究发现，发送的阵列与接收机中所用的本地阵列（或阵列）可以不必相同，而只要这两个阵列（称为阵列偶）满足一定条件，就完全可达到工程上对最佳信号的要求。阵列偶中两个阵列的互相关函数定义为此阵列偶的自相关函数，以此为依据可广泛研究各种形式上的新型最佳信号。

定义2设X=［x（s1，s2，…，sn）］和Y=［y（s1，s2，…，sn）］是两个n维N1×N2×…×Nn阶阵列，其中0≤si≤Ni-1，1≤i≤n，称X和Y组成一个n维阵列偶，记作（X，Y），称V=N1N2…Nn为该阵列偶的体积。若X和Y中的元素取值为±1，则称阵列偶（X，Y）为n维二进阵列偶。一维的阵列偶称为序列偶。

文献［7］中提出了正交矩阵偶的概念，它是正交矩阵的一种扩展，其中的二元正交矩阵偶不受阶数应为2的幂次的限制。

定义3设X和Y为两个M×N阶矩阵，X和Y内元素为±1，若满足XYT=cIM，其中c常数，IM为M阶单位方阵，YT为Y矩阵的转置，则（X，Y）称为二元正交矩阵偶，简称正交矩阵偶［7］。

1.2离散小波变换

离散小波变换具有多分辨率分析、符合人类视觉特性等优点，所以本文选择此小波域嵌入水印。

一级小波分解可以将图像分为低频区域和3个高频区域，小波二级分解是对一级分解的低频区域再次分解，得到一个低频区域和7个高频区域。若将水印嵌入低频区，则鲁棒性好，但有可能降低隐蔽性；而将水印嵌入高频区，则不可见性好，但鲁棒性可能较差。在小波基的选择方面，刘九芬等［8］认为：Haar小波适合于图像水印。综合考虑上述因素，算法中通过Haar小波基进行小波分解，并选择低频区域完成水印嵌入。

1.3奇异值分解

定义4设A∈Rm×n，其中Rm×n是m×n实数域，则矩阵A的奇异值分解为

其中U和V是正交矩阵，S=diag（σ1，σ2，…，σr）是一个非对角线上的项均为0的矩阵，r=min（m，n），其对角线上的元素满足：

上式中，σi是由该分解惟一确定的，称为矩阵的奇异值A，非0奇异值的个数等于矩阵A的秩。

将SVD分解引入到数字水印算法中，一方面图像的奇异值具有很好的稳定性；另一方面，奇异值表现出来的是图像内在代数特性而非视觉特性。因此，利用奇异值的上述特性，可以提高数字水印的鲁棒性。

2　水印的嵌入和提取过程

2.1水印嵌入过程

水印嵌入过程如图1所示。

图1　数字水印嵌入流程图Fig.1The flow chart of digital watermark embedding

1）首先对Lena载体图像a0（M×M）按最佳信号Ma（n×n）的大小分成（i，j=m/n）个子块，将每个子块与最佳信号Ma相乘，从而实现载体图像的时域混合；然后将分块的图像重新组合成C（M×M）。

2）采用Haar小波基对C进行两级离散小波变换，得到6个高频子带和1个低频子带A2，大小为M/4。

3）因水印图像I选取的是m×m的二值图像，故将低频子带按照Bij=round（M/4m）大小的矩阵分块，共分解为m×m个子块Bij，其中i，j=1，2，…，m。

4）对每个子块Bij进行奇异值分解，即Bij=USV，得到3个矩阵U、S、V。对每个矩阵S的对角线元素进行降序排列，保证每个S矩阵对角线的第一个元素σij为最大值。

5）设定嵌入强度因子q，令z=mod（σij，q）；按照下述规则对每个S矩阵的第一个元素σij进行水印的嵌入：

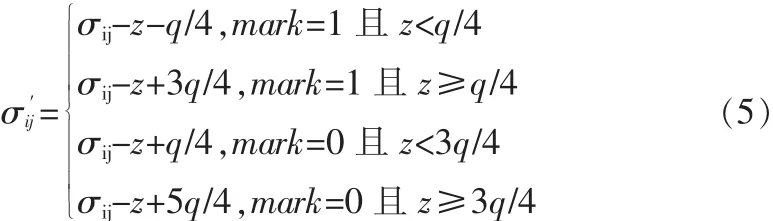
其中，mark为需要嵌入的水印信号。

6）对由σ′ij构成的矩阵S′进行奇异值分解逆运算，即B′ij= US′VT，然后将各个分块重新组合，对组合矩阵进行小波逆变换，得到嵌入水印的混合图像a1。

7）将混合图像按照最佳信号Ma（n×n）的大小进行分块，每块与最佳信号再次相乘，从而实现载体图像的时域混合恢复，得到最终嵌入水印的混合图像C2。

2.2水印提取过程

提取即嵌入的逆过程。

1）对攻击后的嵌入水印图像M1（M×M）按照Ma（n×n）的大小分成（i，j=m/n）个子块，之后每个子块与最佳信号Ma相乘，实现时域混合；然后将分块的图像重新组合成C1（M×M）。

3）找到每块的S矩阵对角线上的最大值σij令z=mod（σij，q），按照下面的规则提取水印：

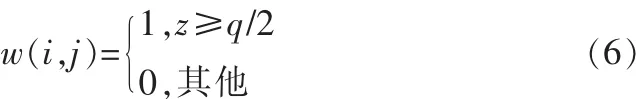
其中，w即为提取的水印信息。

4）对嵌入水印的图像和提取的水印图像分别进行图像质量评价。嵌入水印的图像通过PSNR（峰值信噪比）进行客观评价，体现算法不可见性能的优劣，PSNR计算公式如下：

提取的水印图像通过NC（提取水印与原始水印的互相关系数）进行客观评价，体现算法的鲁棒性，NC计算公式如下：

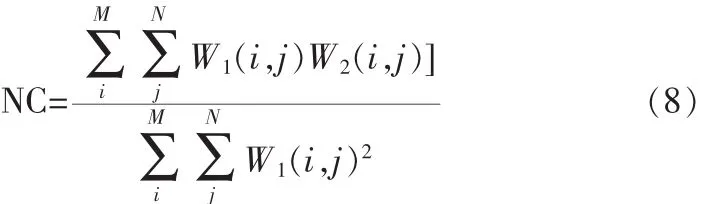
3　实验结果与分析

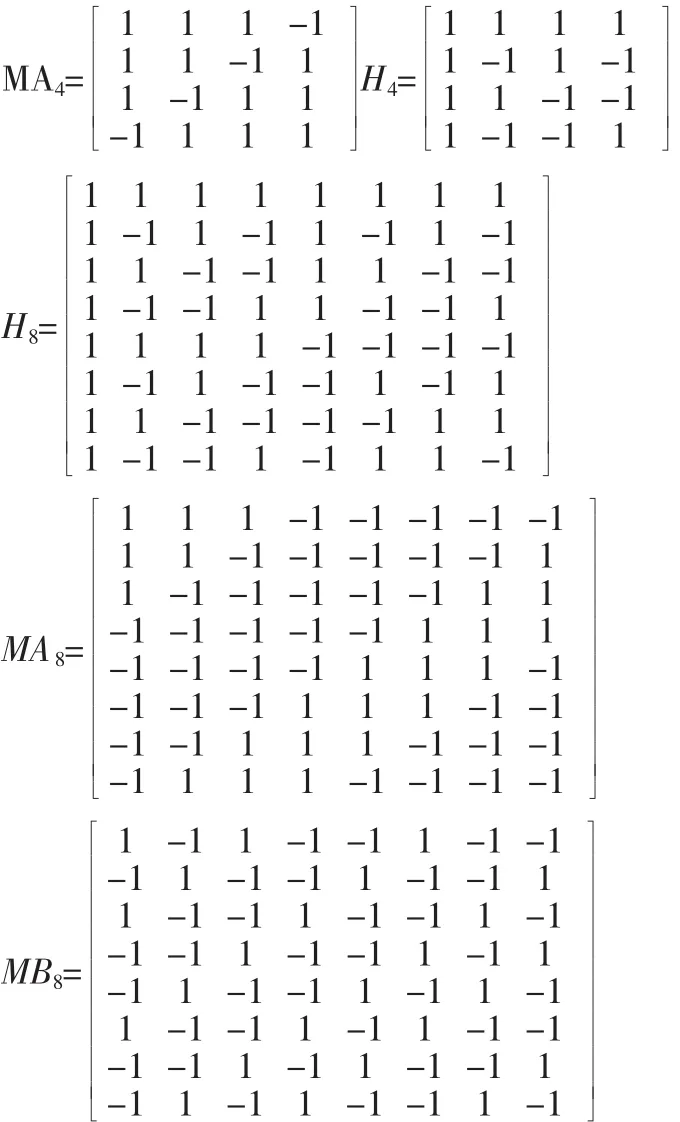
选择lena（512×512）为载体图像，水印选取64×64的二值图像。嵌入强度因子q越大，则鲁棒性越好，但不可见性会相应变差，通过实验，取q=45。最佳信号选择了4阶、8阶、16阶Hadamard矩阵（H4、H8、H16），由最佳二进序列构成的4阶矩阵（MA4），以及8阶、16阶正交矩阵偶（MA8与MB8、MA16与MB16），如下所示。

3.1不同最佳信号的对比分析

3.1.1直接检测不攻击实验测试

分别选取不同的最佳信号通过实验测试，观察嵌入和提取图像的效果，并进行客观评价对比，嵌入后的图像峰值信噪比表格如表1所示。

称取60 mg标准品于2 mL离心管中，按照试剂盒说明书操作提取基因组DNA。利用QIAxpert测定所提DNA溶液浓度，并以A260/A280比值判断DNA的质量。DNA稀释至50 ng/μL备用。

表1　不同最佳信号时域混合的峰值信噪比性能对比Tab.1PSNR performance contrast after different optimal signalmixed in time-domain

已经证明，PSNR大于40才不会造成视觉影响。由表中数据可知，采用16阶正交矩阵偶的嵌入水印图像具有视觉影响，故不适合应用于时域混合。

直接提取的水印与原水印的相关系数表格如表2所示。

表2　不同最佳信号时域混合的相关系数对比Tab.2NC contrast after different optimal signal mixed in time-domain

理论上，NC数据越大，说明提取水印效果越好，与原水印相似度越高。由表2数据可知，在未对嵌入水印的图像进行攻击的情况下，16阶哈达玛矩阵提取的水印图像与原水印图像有差异，故不适合应用于时域混合。

3.1.2攻击实验测试

分别应用由最佳二进序列构成的4阶矩阵（MA4），4阶、8阶哈达玛矩阵、8阶正交矩阵偶进行攻击实验测试，对算法鲁棒性进行对比分析。加入各种攻击后提取的水印图像如图2所示。

图2　经受各种攻击后的水印提取图Fig.2Watermark extraction image after different attack

由上述结果可知，采用4长最佳二进序列构成的4阶矩阵进行时域混合，在各个攻击条件下鲁棒性较好，特别通过高斯低通滤波、JPEG压缩和旋转的处理后，鲁棒性优势表现突出。

各种攻击条件下，提取水印与原水印图像的相关系数值（NC）如表3所示。

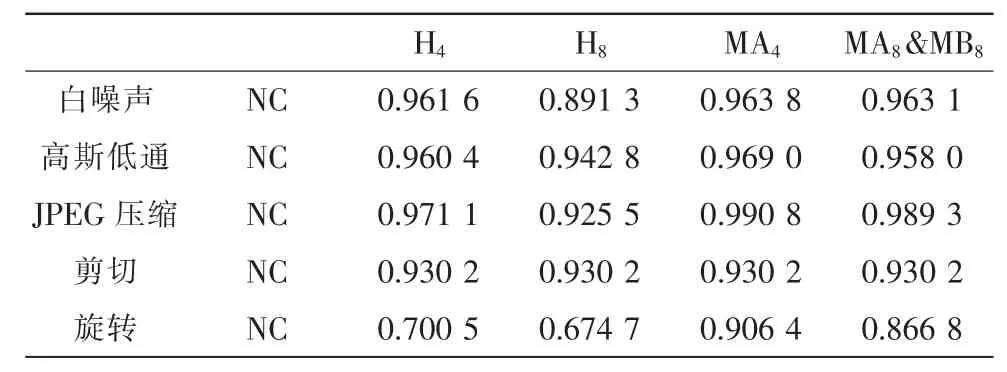
表3　不同攻击条件下提取水印与原水印图像的相关系数Tab.3NC of the extraction watermark image with different attacks and the original watermark image

比较结果如下：

1）白噪，NC：MA4>MA8&MB8>H4>H8

2）低通，NC：MA4>H4>MA8&MB8>H8

3）压缩，NC：MA4>MA8&MB8>H4>H8

4）剪切，NC：MA4=H4=H8=MA8&MB8

5）旋转，NC：MA4>MA8&MB8>H4>H8

因此，应用MA4矩阵的鲁棒性具有明显优势。

上述实验结果表明，由4长最佳二进序列构成的4阶正交矩阵更适用于基于时域混合的水印算法，具有很强的鲁棒性。

3.2与传统DWT-SVD算法的比较分析

将基于时域混合的水印算法和传统DWT-SVD水印算法进行了对比分析，结果如下。

图3　嵌入水印图像的对比Fig.3Contrast of embedded watermark image

由上图可知，两种算法性能接近，视觉效果良好。

两种算法的PSNR值分别为：

PSNR（时域混合DWT-SVD）=49.481 6

PSNR（传统DWT-SVD）=43.440 0

两种算法提取水印的相关系数NC值分别为：

NC（时域混合DWT-SVD）=1.000 0

NC（传统DWT-SVD）=1.000 0

因此，基于时域混合的水印算法在保持传统算法提取效果的情况下，不可见性有明显提高。

4　结论

本文提出了一种基于时域混合的DWT-SVD的新型数字水印技术。对水印算法进行了仿真实验和攻击测试，并与传统DWT-SVD水印技术相比较。实验结果表明，时域混合水印技术具有较好的鲁棒性。其中，采用4长最佳二进序列构成的4阶矩阵进行时域混合操作，不可见性和鲁棒性最佳。与传统DWT╞SVD水印技术相比，时域混合DWT-SVD水印技术具有更好的隐蔽性，具有一定应用前景，值得进一步深入研究。

［1］贺元香，史宝明，李恒杰.一种改进的抗几何攻击彩色图像水印算法［J］.自动化与仪器仪表，2014（1）：101-105 HE Yuan-xiang，SHI Bao-ming，LI Heng-jie.An improved resistance to geometric attack color image watermarking algotithm［J］.Automation&Instrumentation，2014（1）：101-105.

［2］雷蕾，郭树旭，王雷.基于小波变换的SVD数字图像水印算法研究［J］.计算机仿真，2013，30（9）：169-260. LEI Lei，GUO Shu-xu，WANG Lei.SVD digital image watermarking algorithm based on wavelet transform［J］.Computer Simulation，2013，30（9）：169-260.

［3］朱岩，杨永田.扩频CDMA水印性能分析及其应用研究［J］.哈尔滨工业大学学报，2006，38（12）：2116-2120. ZHU Yan，YANG Yong-tian.Performance analysis of spread spectrum CDMA watermarking and applied research［J］．Journal of Harbin Institute of Technology，2006，38（12）：2116-2120.

［4］胡青，龙冬阳．基于DWT-SVD的奇异向量量化水印算法［J］．计算机科学，2011，38（11）：30-33，53. HU Qing，LONG Dong-yang.Singular vertor quantization watermarking scheme based on DWT-SVD［J］．Computer Science，2011，38（11）：30-33，53.

［5］Bhatnagar G，Raman B.A new robust reference water-marking scheme based on DWT-SVD［J］.Computer Standards& Interfaces，2009，31（5）：1002-1013.

［6］李刚．最佳离散信号偶理论研究［D］.秦皇岛：燕山大学，2006.

［7］刘凯，许成谦，李刚.二元二值周期自相关序列偶的应用研究［J］.电子与信息学报，2009，31（7）：1536-1541 LIU kai，XU Cheng-qian，LI Gang.Research on application of binary sequence pairwith two-Level periodic autocorrelation［J］．Journal of Electronics&Information Technology，2009，31（7）：1536-1541.

［8］刘九芬，黄达人，胡军全．数字水印中的正交小波基［J］．电子与信息学报，2003，25（4）：453-459. LIU Jiu-fen，HUANG Da-ren，HU Jun-quan.Orthogonal wavelet in digital watermarking［J］.Journal of Electronics&Information Technology，2003，25（4）：453-459.

［9］周万府，林加华，薛文格，等.基于混沌、HVS和小波变换的自适应数字水印算法［J］.现代电子技术，2013（14）：76-78. ZHOU Wan-fu，LIN Jia-hua，XUE Wen-ge，et al.daptive image watermarking algorithm based on chaos，HVS and wavelet transform［J］.Modern Electronics Technique，2013（14）：76-78.

［10］姜军，王朝霞，卓嘎，等.一种基于曲波变换的数字水印算法［J］.电子科技，2013（3）：143-146. JIANG Jun，WANG Zhao-xia，ZHUO Ga，et al.Research on watermarking algorithm based on curvelet transform［J］.Electronic Science and Technology，2013（3）：143-146.

DWT-SVD blind digital watermarking algorithm based on the mix of time-domain

ZHANG Feng-juan，LI Qi，GAO Jun-ping，QIN Li-wei
（Information Engineering College，Hebei University of Technology，Tianjin 300401，China）

A new blind digital watermarking algorithm based on the mix of time-domain is proposed.This algorithm changes the traditional watermark embedding process.Firstly，the host image is separated into different blocks，and the perfect signals are used to finish the mix of time-domain on the host image，which changes the distribution of image information.Then，the embedding process is completed on frequency-domain，which is discrete wavelet transform with singular value decomposition，and restore the mix of time-domain to get the image with watermark.Attack tests and comparison with traditional DWT-SVD image watermarking algorithm are carried out.The results show that the image watermarking algorithm based on the mix of time-domain has good imperceptibility and robustness.

digital watermarking；mix of time-domain；perfect signal；DWT；SVD

TN911.73

A

1674－6236（2015）09-0104-05

2014-09-12稿件编号：201409096

河北省自然科学基金（F2012202116）

张凤娟（1988—），女，河北藁城人，硕士。研究方向：图像处理与数字水印技术。