基于微分几何的离合器接合过程速度跟踪滑模控制

赵　韩　邱明明　黄　康

合肥工业大学,合肥,230009

基于微分几何的离合器接合过程速度跟踪滑模控制

赵韩邱明明黄康

合肥工业大学,合肥,230009

针对离合器控制系统中存在的非线性、外部干扰和参数不确定问题,提出了基于微分几何的离合器接合过程速度跟踪滑模控制方法。考虑系统参数的不确定性和外界干扰等不确定因素，建立了单个离合器起步动力学模型;基于微分几何的反馈线性化方法,得出系统的控制律;采用基于趋近律的滑模控制方法,设计了存在不确定干扰的离合器控制系统滑模控制器。利用Lyapunov理论对系统的稳定性进行了证明。仿真结果表明该控制器使离合器接合过程的速度跟踪精度高，且鲁棒性好。

微分几何；离合器；速度跟踪；滑模控制

0　引言

在汽车起步阶段,搭载双离合自动变速器的车辆可以根据其独特的离合器机械偶联结构来选择单离合器起步还是双离合器起步。但是无论采取哪种起步方式,主要的控制目的均是实现离合器与发动机的协调控制，以确保车辆良好的乘坐舒适性。由于采用单离合器起步时，DCT与AMT两种离合器起步方式的动力学原理相同，且两种离合器的控制策略可以相互通用，因此本文的研究对象为DCT离合器单离合器起步的接合过程。

对于汽车起步过程控制而言,离合器的接合品质直接影响到车辆起步的平稳性，同时也关系到离合器的磨损和动力能量损耗等，而离合器的控制策略的优劣又直接决定了离合器的接合品质的好坏。因此,国内外学者在此方面已经开展了广泛深入的研究。Kulkarni等[1]以MATLAB/Simulink数值仿真平台为依托,建立了工程化的DCT系统动态分析模块,采用单离合器起步模式,对发动机与离合器进行最优转矩匹配控制;秦大同等[2]建立了DCT两离合器起步动力学模型,利用模糊控制理论对两离合器的接合速度的控制策略进行了研究;Galvagno等[3]研究了一种考虑了所有功率流路径配置的DCT变速器的运动学和动力学特性,建立了可以方便集成在一个汽车模型的一组方程索引列表，从而可以对特定的挡位和换挡过程进行描述；李瑜婷等[4-5]利用二次型最优控制算法对起步离合器接合压力进行了仿真分析;Michalk等[6]介绍了基于概念的双离合自动变速器控制系统模型，利用简化的车辆模型提出了换挡的前馈控制方法;赵治国等[7]建立了DCT起步过程发动机转速及离合器转矩的计算公式,采用遗传算法在线滚动优化发动机转速及车速目标跟踪曲线,并设计了滑模变结构起步协调控制策略;程东升等[8]建立了AMT离合器液压系统的非线性动力学模型,将反馈线性化与滑模控制相结合设计了非线性控制器;孙承顺等[9]建立了AMT离合器动力学系统和控制系统的数学模型，应用微分几何的反馈线性化方法，将原非线性系统等价为完全可控线性系统，然后设计了滑模控制器。

上述研究主要针对的是离合器接合的控制规律,但大多未考虑模型的非线性、参数不确定性和外部环境的干扰影响,或者考虑了系统的非线性因素，但是未考虑发动机与离合器的协调控制因素。目前线性系统的控制理论已相当完备，但对具有强非线性的物理系统，仍不具有理想的直接控制效果。针对上述问题,本文建立了DCT车辆单个离合器起步的非线性不确定动力学模型，利用微分几何反馈线性化方法求解了系统的控制律，采用趋近律滑模控制方法设计了系统的控制器,利用Lyapunov理论证明了系统的稳定性,同时,对起步时离合器接合过程的速度跟踪情况进行了仿真分析。

1　单离合器起步动力学模型

1.1DCT模型的简化

汽车DCT传动系统是由多个子系统组成的复杂系统，在研究传动系统的动态特性之前，需要对模型进行必要的简化，为此作如下假设:①基于系统中弹性元件质量较小,而惯性元件的刚度较大的原因,忽略系统弹性元件的惯性和惯性元件的弹性;②基于系统中间隙和横向振动小且难以测量的原因，忽略系统的间隙和轴的横向振动；③基于轴承座和齿轮刚度大的原因，忽略轴承座的弹性变形及齿轮的啮合弹性;④基于离合器摩擦片采用冷却油冷却的原因,忽略摩擦片的热衰退。双离合自动变速器有两个输入轴，分别连接变速器的奇数挡齿轮和偶数挡齿轮。发动机输出扭矩分别通过两个离合器与不同的输入轴连接，传给变速器扭矩。根据上述假设，将DCT简化为如图1所示的动力学模型，图中,Te为发动机输出扭矩,Tc1为离合器传动的扭矩,Ie为发动机输出轴和离合器主动盘的当量转动惯量,Tr为负载阻力矩,Iv为离合器之后的传动系包括整车平移质量折算到离合器输出轴上的等效转动惯量和离合器从动片的转动惯量,be为发动机输出轴与离合器主动盘之间的等效的旋转黏性阻尼系数,bv为离合器之后的传动系的等效旋转黏性阻尼系数,ωe、ωv分别为发动机输出转速和离合器输出转速。

图1　起步离合器接合过程模型

1.2起步动力学模型

DCT起步过程中,离合器1逐渐接合,Tc1逐渐增大,而离合器2始终保持分离状态,不传递扭矩,因此发动机的扭矩只通过离合器1传递至车轮,根据受力情况可得起步的系统动力学模型为

(1)

将动力学方程转换为状态方程的形式,令

x1=ωe,x2=ωv,x3=Te，x4=Tcl

其状态方程为

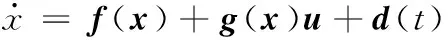
(2)

y=h(x)=[g1(x)g2(x)]

(3)

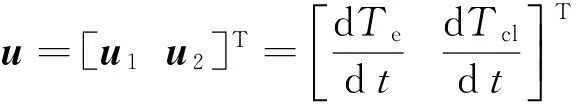
将系统建模误差、参数变化及其他不确定因素视为外界扰动w(x),则

w(x)=Δf(x)+Δg(x)+d(t)

(4)

式中，Δf(x)、Δg(x)为系统建模误差。

2　反馈线性化控制律

以微分几何理论为基础，通过输入输出反馈线性化，求得反馈控制律。系统控制框图如图2所示。

图2　系统控制框图

将式(2)看作一般的MIMO非线性系统,其中状态x是n维的,输入和输出均为二维。

对于DCT车辆起步过程的数学模型,可通过微分几何法的原理,将系统进行反馈线性化，求解反馈线性化控制律。 通过计算得

(5)

从而得

(6)

由此可得,系统的相对阶r1=2。

同理可得：

(7)

(8)

由此可得,系统的相对阶r2=2。则系统的相对阶向量(r1r2)存在,且满足r1+r2=n=4,根据状态空间精确线性化可解的条件[10]可知，系统的状态空间可精确线性化，且通过线性化的系统是可控的。

根据反馈线性化理论，令

(9)

(10)

则反馈线性化控制律为

(11)

(12)

定义系统的输出参考为yd,则跟踪误差向量为

e=yd-y

(13)

取两个输出的期望值分别为x1d和x2d,则输出速度的跟踪误差为

e=[x1d-x1x2d-x2]T=[e1e2]T

(14)

3　速度跟踪控制器的设计

上述反馈线性化控制律要求外界干扰w已知,而实际工程应用中外界干扰w往往不能确定。因此,当系统中存在未知的不确定项时,采用微分几何方法求得的控制律将不再满足控制需要，这会严重影响到控制效果。为解决这一问题,本文采用了鲁棒性好、响应速度快,且控制算法简单的基于趋近律的滑模控制方法对控制器进行设计。

3.1滑模控制器的设计

对反馈线性化后的系统取滑模函数为

(15)

式中,c为滑模控制器的参数矩阵，c=[c1c2]。

则

(16)

取指数趋近律为

(17)

将式(16)和式(17)合并,从而求得v1和v2,即

(18)

(19)

则控制律为

(20)

(21)

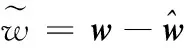
(22)

(23)

式中,β为设计常数矢量，其元素均大于0。

为了对不确定项和外部干扰进行补偿,以满足到达条件，设计控制律为

(24)

(25)

将式(24)和式(25)的控制律代入式(17)得

(26)

3.2滑模控制器稳定性证明

取Lyapunov函数为

(27)

则

(28)

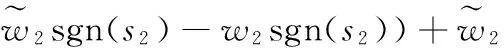
(29)

将式(22)代入式(28)、式(29)得

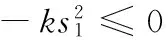
(30)

(31)

由此可知系统稳定。

4　仿真结果分析

根据前述的起步时离合器接合动力学模型及控制器，利用MATLAB/Simulink建立离合器接合过程速度跟踪控制仿真模型，如图3所示。

图3　离合器速度跟踪控制仿真模型

仿真参数如下:Ie=0.28 kg·m2,Iv=2.1 kg·m2,Tr=30 N·m,be=0.01 N·m·s,bv=0.01 N·m·s,ωe=120 rad/s。取c1=c2=5,k=5,ε=0.5,系统总干扰设定为w1=Asin(2πt),w2=Bcos(2πt),仿真结果(工况一)如图4～7所示。

(a)发动机转速跟踪曲线

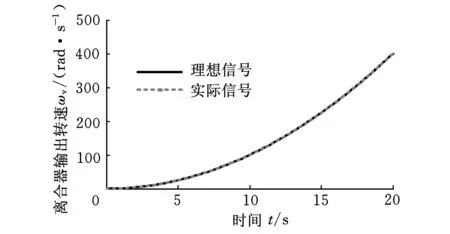
(b)离合器输出转速跟踪曲线图4　系统输出跟踪曲线(工况一)

(a)发动机转速跟踪曲线

(b)离合器输出转速跟踪误差图5　系统输出跟踪误差(工况一)

图4为发动机转速和离合器从动端的转速跟踪情况,在7.74 s以后离合器完全接合,从图中可以看出，采用本文设计的控制器，对于存在不确定干扰的离合器起步时的控制系统,发动机转速和离合器输出转速能够迅速收敛于参考输入值，对干扰具有很强的抗干扰能力。图5为系统输出的跟踪误差,从图中可以看出,控制器的跟踪精度高。

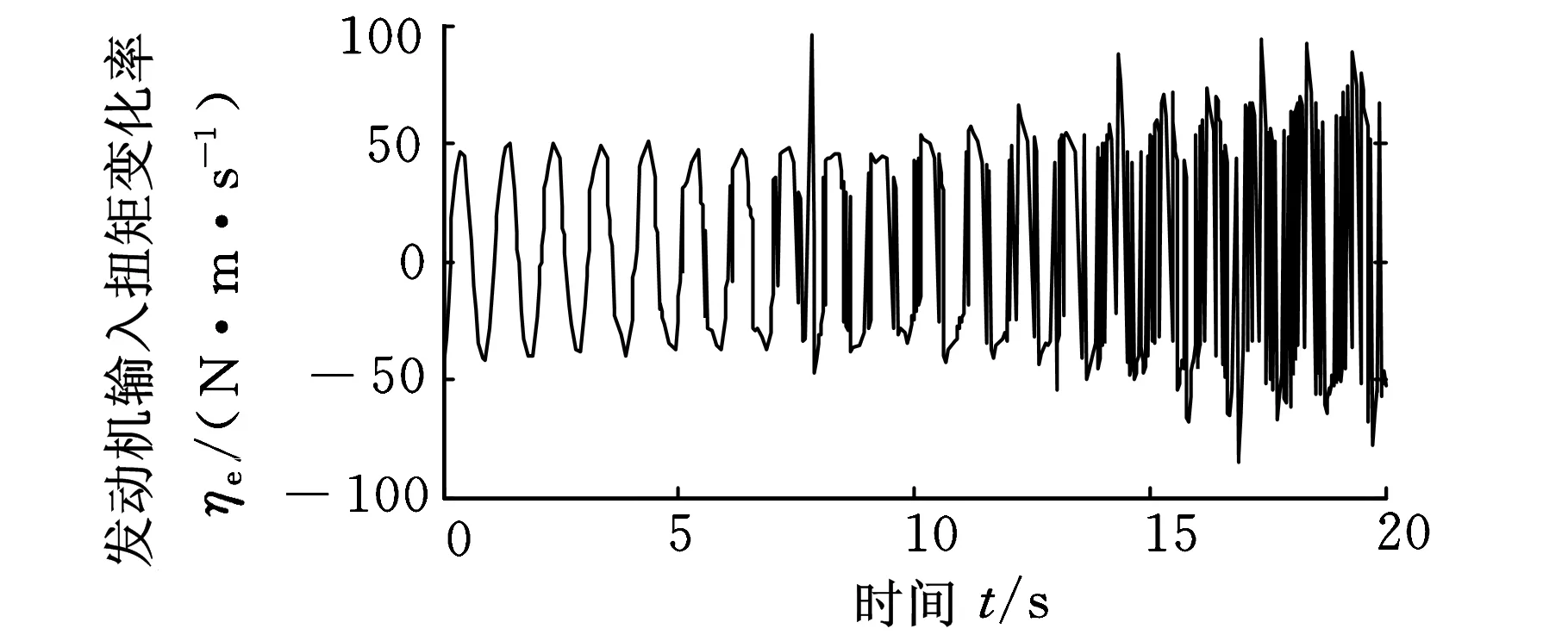
(a)系统的控制输入u1

(b)系统的控制输入u2图6　系统控制输入(工况一)

图7　系统的干扰(工况一，A=2，B=3，f=1 Hz)

图6为系统的控制输入,从图中可以看出，在起步过程中发动机的扭矩变化率和离合器输出的扭矩变化率小，这说明整个系统的冲击度小。在离合器主动盘、从动盘接合的瞬间，发动机的扭矩变化率出现小的波动,这时由于本文设置的初始负载扭矩Tr=30 N·m较大,导致离合器在接合的瞬间发动机输出扭矩出现波动。而此时离合器传递的扭矩变化率未出现突变，这是由于本文提出的控制器已经考虑了发动机扭矩波动干扰，仿真结果进一步验证了控制器的鲁棒性。

为进一步检验控制器的有效性,增大干扰的幅值和频率(A=20，B=30,f=2 Hz),另外改变起步工况,即改变发动机和离合器速度跟踪目标，缩短离合器接合时间，得到如图8～图14所示的结果。

由图8～10可以看出,当系统的不确定干扰的幅值和频率均增大时，系统的输出跟踪精度仍然很高，且系统的控制输入未出现大的波动，从而证明控制器的高鲁棒性。

(a)发动机转速跟踪曲线

(b)离合器输出转速跟踪曲线图8　系统输出跟踪曲线(工况二)

(a)发动机转速跟踪误差

(b)离合器输出转速跟踪曲线图9　系统输出跟踪误差(工况二)

由图12～图14可知,在5.47 s以后离合器完全接合,离合器接合时间较图4、图8两种工况缩短约2.3 s时，控制器仍具有良好的跟踪精度和鲁棒性。

5　结语

(a)发动机转速跟踪误差

(b)离合器输出转速跟踪曲线图10　系统控制输入(工况二)

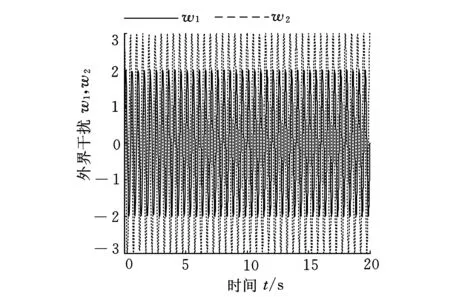
图11　系统的干扰(A=20,B=30,f=2 Hz)

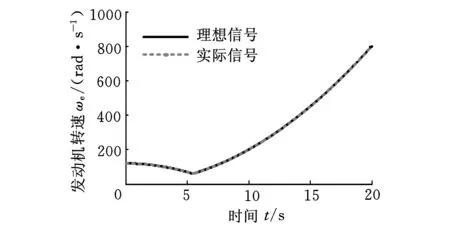
(a)发动机转速跟踪曲线

(b)离合器输出转速跟踪曲线图12　系统输出跟踪曲线(工况三)

(a)发动机转速跟踪误差

(b)离合器输出转速跟踪误差图13　系统输出跟踪误差(工况三)

(a)系统的控制输入u1

(b)系统的控制输入u2图14　系统控制输入(工况三)

本文将非线性控制器和滑模控制方法用于实现起步过程中离合器速度跟踪控制。采用微分几何的反馈线性化理论设计了系统的控制律，针对系统中存在的不确定干扰，设计了干扰上界的估计值的自适应律，利用基于趋近律的滑模控制方法设计了系统的控制器。该控制器不需要精确知道干扰项，利用滑模控制提高了系统的鲁棒性。利用Lyapunov稳定性理论分析了系统的稳定性。仿真结果表明，本文所提出的控制器具有良好的鲁棒性和跟踪性能。

[1]Kulkarni Manish,Shim Taehyun,Zhang Yi.Shift Dynamics and Control of Dual-clutch Transmissions[J].Mechanism and Machine Theory,2007,42(2):168-182.

[2]秦大同,刘永刚,胡建军,等.双离合器式自动变速器两离合器起步控制与仿真[J].机械工程学报,2010,46(18):121-127.

Qin Datong,Liu Yonggang,Hu Jianjun,et al.Control and Simulation of Launch with Two Clutches for Dual Clutch Transmissions[J].Journal of Mechanical Engineering,2010,46(18):121-127.

[3]Galvagno E,Velardocchia M,Vigliani A.Dynamic and Kinematic Model of a Dual Clutch Transmission[J].Mechanism and Machine Theory,2011,46(6):794-805.[4]李瑜婷,赵治国,章桐.DCT变速器双离合器压力最优控制方法的仿真研究[J].中国机械工程,2010,21(12):1496-1501.

LiYuting,ZhaoZhiguo,ZhangTong.ResearchonOptimalControlofTwinClutchEngagementPressureforDualClutchTransmission[J].ChinaMechanicalEngineering,2010,21(12):1496-1501.

[5]吴光强，张德明.基于最优控制理论的DCT离合器升档作动方式的研究[J].汽车工程，2009,31(3):258-261.

WuGuangqiang,ZhangDeming.AResearchontheWayofClutchActuationDuringDCTUpshiftBasedonOptimalityTheory[J].AutomotiveEngineering,2009,31(3):258-261.

[6]MichalkaA,RoppeneckerG,WurmthalerC,etal.AModelBasedControlApproachforDualClutchTransmissionsasPartofaNewTransmissionControlConcept[J].At-Automatisierungstechnik,2009,5(57):230-237.

[7]赵治国,胡笑天,姜娇龙,等.干式双离合器自动变速器起步滑模变结构协调控制及实时优化[J].机械工程学报,2012,48(24):87-105.

ZhaoZhiguo,HuXiaotian,JiangJiaolong,etal.SlipModeVariableStructureCoordinatingControlandReal-timeOptimizationofLaunchforDryDualClutchTransmission[J].JournalofMechanicalEngineering,2012,48(24):87-105.

[8]程东升,顾力强,张建武.基于反馈线性化的汽车AMT离合器滑模控制[J].汽车工程,2002,24(5):384-386.

ChengDongsheng,GuLiqiang,ZhangJianwu.SlidingModeControlforElectricallyControlledClutchofAMTBasedonFeedbackLinearization[J].AutomotiveEngineering,2002,24(5):384-386.

[9]孙承顺,张建武,程东升.反馈线性化与滑模控制方法在汽车AMT中的应用[J].系统仿真学报,2004,16(4):630-633.

SunChengshun,ZhangJianwu,ChengDongsheng.ApplicationofFeedbackLinearizationandSlidingModeControltoAMTofVehicles[J].JournalofSystemSimulation,2004,16(4):630-633.

[10]李殿璞.非线性控制系统[M].西安：西北工业大学出版社，2009.

(编辑卢湘帆)

Sliding Mode Control for Speed Tracking Based on Differential Geometry during Clutch Engaging Process

Zhao HanQiu MingmingHuang Kang

Hefei University of Technology,Hefei,230009

Aimed at nonlinearity,external disturbances and parameter uncertainty of the clutch control system,a sliding mode control was put forward based on differential geometry for speed tracking during clutch engaging process.Considering the uncertainty of system parameters and external disturbances and other uncertain factors, a single clutch dynamic system model was established,feedback linearization was used based on differential geometry method,the control law was obtained,and then a sliding mode controller was designed based on reaching law control method for the clutch control system with disturbance.The stability of the system was proved by using Lyapunov theory.The simulation results show that the controller can make the process of clutch engagement speed tracking accuracy and robustness.

differential geometry;clutch; speed tracking;sliding mode control

2014-08-20

国家高技术研究发展计划(863计划)资助项目(2012AA111711)

U463DOI：10.3969/j.issn.1004-132X.2015.17.005

赵韩，男,1957年生。合肥工业大学副校长、教授、博士研究生导师。主要研究方向为机械学。发表论文50余篇。邱明明,男,1983年生。合肥工业大学机械与汽车工程学院博士研究生。黄康,男,1968年生。合肥工业大学机械与汽车工程学院副院长、教授、博士研究生导师。