一种盘式制动器钳体轻量化设计研究

唐进元　赵国伟

中南大学高性能复杂制造国家重点实验室，长沙，410083

一种盘式制动器钳体轻量化设计研究

唐进元赵国伟

中南大学高性能复杂制造国家重点实验室，长沙，410083

以体积和疲劳寿命为轻量化设计目标，采用计算机辅助集成技术对盘式制动器的钳体进行轻量化设计。利用有限元分析方法计算制动盘制动力矩并将其与实验测得的制动力矩进行比较，验证了有限元分析的步骤与方法正确可行；结合有限元分析得到的钳体的最大主应力，根据名义应力法和Smith方法计算钳体疲劳寿命；通过ISIGHT集成CATIA、ABAQUS和MATLAB对钳体进行轻量化设计。

制动钳体；轻量化；有限元分析；制动力矩；疲劳寿命

0　引言

汽车制动器主要分为盘式制动器和鼓式制动器，是汽车制动系统的主要零部件。盘式制动器由于其热稳定性好、水稳定性好、制动力矩平稳、制动块上压力分布均匀、噪声低等优点在汽车行业中得到了广泛应用[1]。由于汽车制动性能的好坏直接关系到驾驶员和乘客的生命安全，因此制动器的设计是汽车设计中一项非常重要的工作。

目前，盘式制动器的研究主要涉及制动器的设计、加工以及制动性能的分析与提高等方面[2]。Hohmann等[3]建立了盘式制动器的有限元模型，对制动过程中接触压力的分布情况进行了研究。Liu等[4]利用ABAQUS通过复特征值法对盘式制动器制动过程中的尖叫现象进行了研究。Belhocine等[5]通过ANSYS对不同型号和不同材料的制动盘在制动过程中的热现象进行了仿真分析。有关制动器的轻量化研究还处于起步阶段，随着汽车轻量化设计的发展，有必要对制动器进行轻量化设计。

现有的轻量化设计方法大都是改变零件的材料，使用质量更小、机械性能更好的材料来代替原有材料[6]；或先用CAE软件进行有限元分析，然后将应力较小的区域去掉[7]；或利用多目标遗传算法，对机械零部件的近似模型进行优化[8]。上述三种方法中，第一种方法改变材料后会提高机械零件的制造成本；第二种方法需要进行多次建模和分析，工作量大且难以确定最佳的优化结果；第三种方法需要对模型进行大量的简化，难以实现对复杂模型的轻量化。

本文不改变零件的材料，在保证疲劳寿命的情况下对盘式制动器的制动钳体进行轻量化设计。首先通过有限元分析和实验相结合的方法对盘式制动器制动力矩进行分析验证；然后根据有限元计算得到的应力结果和材料的性能参数来计算钳体的疲劳寿命；最后使用计算机辅助优化软件ISIGHT集成CATIA、ABAQUS和MATLAB对制动钳体进行参数优化。优化过程中计算机自动更改优化变量的值，并自动调用相关软件进行分析计算，既节省时间又减少设计者的工作量，同时还能得到较好的轻量化结果。

1　盘式制动器有限元分析

1.1有限元模型

图1　盘式制动器有限元模型的约束与加载情况

文本所用盘式制动器的有限元模型由制动盘、钳体、制动块和活塞组成[3]。被简化的零部件对当前零部件的作用通过约束、载荷或边界条件的形式施加到模型中。为了便于优化时对优化参数进行更改，盘式制动器相关零件的三维模型在CATIA中创建，通过STEP文件将其导入到ABAQUS中进行有限元分析。在ABAQUS中通过映射网格划分方法将制动盘、制动块和活塞划分为六面体网格，为了便于优化设计将钳体划分为四面体网格，划分网格后的有限元模型如图1所示。1.2约束与加载

当盘式制动器制动时，钳体内部液压缸中的液体压力推动活塞运动，使与活塞连接的制动块与制动盘接触，其反作用力推动钳体运动并将压力传递到另一侧的制动块使其与制动盘接触，以此来实现对汽车的制动[3]。

在有限元模型中，我们将液体压力施加给钳体和活塞的相应位置(图1b)。活塞与制动块和钳体与制动块相接触的面之间建立绑定约束；制动块和制动盘之间建立接触约束，设置摩擦因数为0.4。钳体与导向销连接的孔与其中心的参考点耦合，制动盘内孔表面与其对应的参考点建立耦合约束。

盘式制动器的分析分为两步进行(图1c)，第一步给钳体和活塞施加大小为p0的压力载荷，使制动块与制动盘充分接触并将其压紧；第二步通过参考点RP-1使制动盘沿其轴线方向转动。在整个过程中通过边界条件使钳体和制动块只能沿制动盘的轴线方向移动，使制动盘只能沿其轴线方向转动。

1.3结果分析

根据有限元分析结果，盘式制动器中的最大主应力出现在钳体上，其大小和分布情况如图2所示。

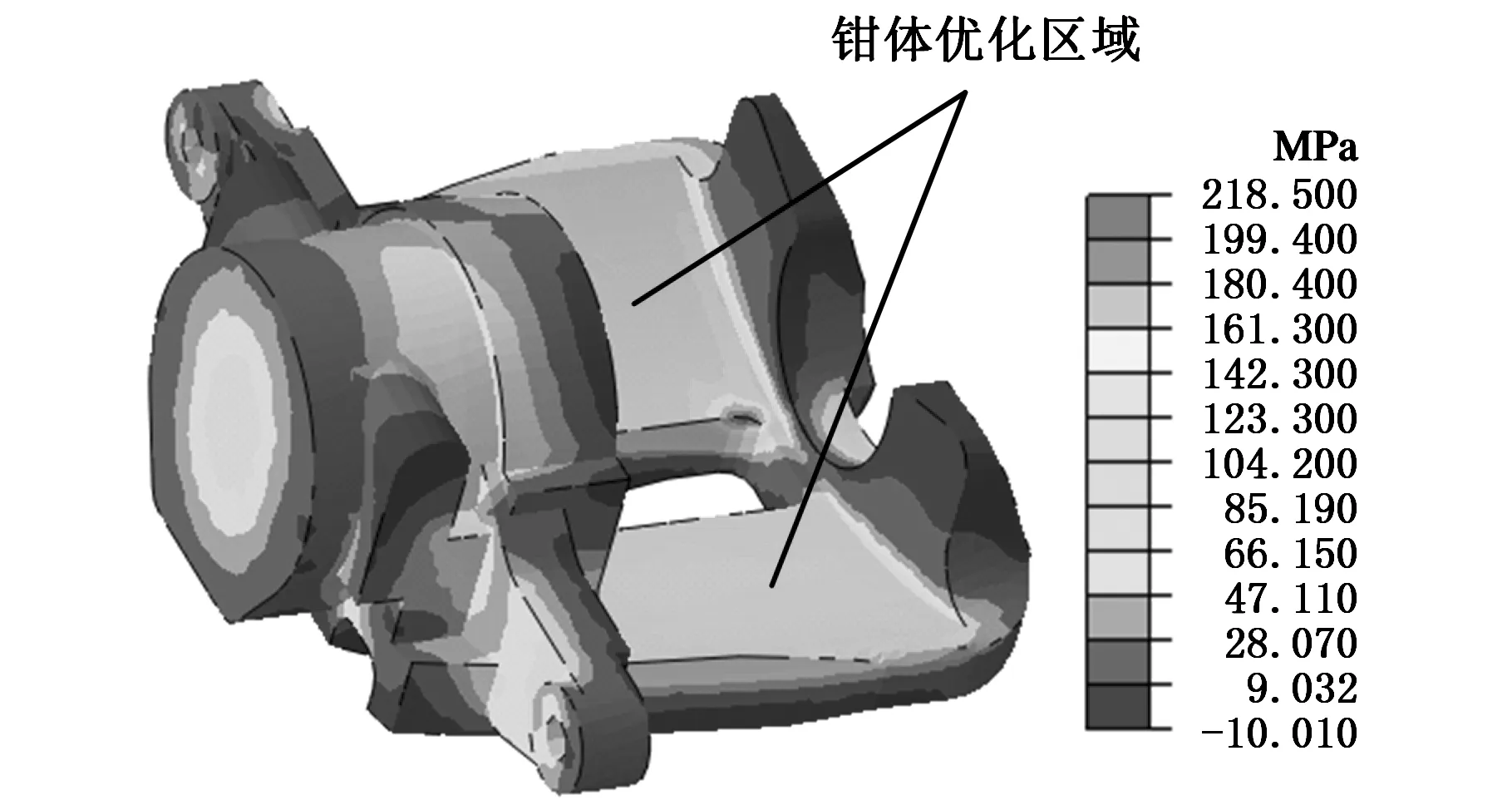
图2　制动钳体的最大主应力分布

在ABAQUS的后处理模块中可以得到制动盘受到的制动力矩。有限元分析和实验获得的制动力矩的值如图3所示。

图3　有限元分析和实验得到的制动力矩

对比图3中的两条曲线可以看出，有限元分析的过程与制动器实际制动过程基本一致，即在制动块与制动盘产生相对运动之前制动力矩为0，开始制动后制动力矩在很短的时间内达到最大值，并保持在该值附近波动直到制动结束。

由图3可知，有限元分析得到的制动力矩的大小为2106 N·m，实验测得的制动力矩大小为1883 N·m。实验测得的制动力矩偏小，与有限元分析结果的误差为10.6%。引起实验测得的制动力矩偏小的原因主要是在有限元分析中没有考虑液压泵的机械效率，而是直接将液压泵的压力p0代入进行计算和分析。实际过程中，汽车盘式制动器液压泵的机械效率一般取0.85～0.95[9]，所以引起实验测得的制动力矩比有限元分析结果小是正常的。结合上述有限元分析和实验测得的制动力矩的对比结果，可以说明有限元分析得到的结果与真实情况接近，验证了有限元分析结果的准确性。

图3中有限元分析值相对于实验值有一些滞后是因为该分析步的初始时间的取值偏大(这样做可以提高分析速度)。减小初始时间可以减小两者之间的差异，但分析速度过慢不利于之后的轻量化设计。

2　钳体的疲劳寿命计算

2.1SN曲线的修正

根据SN曲线来判断零件的疲劳寿命时，为了准确地计算出零件的疲劳寿命，首先需要对SN曲线进行修正。SN曲线通常都是在一定实验条件下获得的，当机械零件的实际工作条件和实验条件不一致时需要对其SN曲线做相应的修正[10]。

SN曲线修正的关键是对疲劳极限进行修正。对疲劳寿命的修正主要根据不同的应力比、尺寸、表面精度和温度等因素的影响进行修正。盘式制动器制动时的外载荷为液压泵提供的液体压力。本文所用载荷的施加方式与对盘式制动器进行疲劳测试时的加载方式相同。在疲劳测试时，车轮制动时液压泵的压力从0增大到p0，然后再卸载。因此，盘式制动器在实验工况下的应力循环可以近似为脉动循环，记脉动疲劳极限为σ0。

2.1.1疲劳极限的修正

钳体的材料为QT450-10，材料参数如表1所示[11-12]，其中σ-1为对称循环应力下指定存活率为95%时的疲劳极限。根据相关手册无法查阅该材料σ0的值，可以根据Smith图来近似计算σ0[13]。

表1　QT450-10的材料参数

Smith图是以平均应力σm为横坐标，最大应力σmax和最小应力σmin为纵坐标的疲劳极限线图，如图4所示。图4中,A点表示对称疲劳极限σ-1，D点表示脉动疲劳极限σ0，C点表示强度极限σb，曲线ADC为最大应力线，曲线BEC为最小应力线。曲线ADC与曲线BEC所包围的面积表示不产生破坏的应力水平。

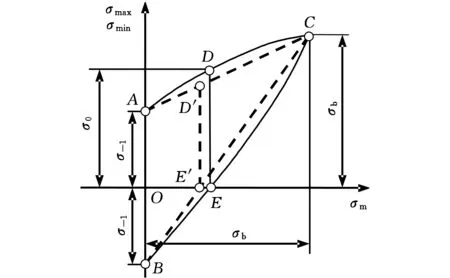
图4　Smith图

由图4可以看出，D点的横坐标为BEC线与横轴的交点(E点)。连接AC和BC(图4中虚线所示)，可得到BC线与横轴交于点E′，通过E′作横轴的垂线交AC于点D′，D′对应的纵坐标即为所求得的σ0。将表1中的数据代入图4计算得σ0=300 MPa。上述方法计算得到的σ0的值比实际情况要小，这样得到的SN曲线偏于保守。

机械零件的尺寸、表面精度和环境温度等因素对疲劳极限的影响通过相应的影响系数来衡量[14]。本文考虑钳体的尺寸和表面精度对疲劳极限的影响。记尺寸系数为Csize，表面加工系数为Csurf。根据相关手册查得Csize和Csurf的值如表2所示。修正后的脉动疲劳极限为

(1)

相对于对称疲劳极限σ-1的综合修正系数为

(2)

表2　QT450-10材料的疲劳参数

2.1.2SN曲线的修正

图5中，曲线Ⅰ为QT450标准试样在对称循环载荷下存活率为95%的SN曲线[11]。运用疲劳综合修正系数对材料的SN曲线进行修正可以得到零件的SN曲线。由式(2)可得

σ′=σ/kσ

(3)

式中，σ′为作用于零件上的名义应力；σ为作用于标准试样上的名义应力。

图5　修正前后的SN曲线

在高周疲劳区域，零件的SN曲线可表示为

(σ′kσ)mN=σmN=C

(4)

式中，m为材料常数。

由式(4)可得修正后的SN曲线，即图5中的曲线Ⅱ。

2.2疲劳寿命计算

当计算出零件的应力后，将其代入上述SN曲线中即可算得零件的疲劳寿命。通过SN曲线计算得到的是零件断裂失效的疲劳寿命。

据统计，裂纹萌生寿命占零件总寿命的90%以上[15]，因此也可以使用零件的裂纹萌生寿命来估算机械零件的疲劳寿命。Smith等提出了一种计算裂纹萌生疲劳寿命的方法[16](以下简称SWT公式)：

(5)

材料疲劳参数的取值如表2所示。

上述SN曲线和材料的疲劳参数都是在单轴拉压的条件下测得的，因此本文根据钳体受到的最大主应力来计算疲劳寿命。将有限元分析得到的最大主应力代入SN曲线和SWT公式中计算得到的轻量化前的钳体的疲劳寿命分别为2.32×106次和2.07×106次。在对制动器进行疲劳测试时，只要经过2×105次循环后制动器没有发生破坏即可视为合格。因此钳体还有一定的轻量化空间。

3　轻量化设计

3.1轻量化流程

本文所用轻量化设计的思路是通过计算相关优化变量在不同尺寸下的体积和疲劳寿命来确定最终的优化尺寸。图6为本文所用轻量化设计的流程图。由图6可以看出，在轻量化开始之前首先要确定轻量化对象并确定需要优化的位置。

图6　轻量化设计流程图

本文的轻量化对象为钳体，要优化的位置为钳体内侧凹槽(图2)。确定好轻量化对象后在CATIA中建立用于有限元分析的模型，并通过宏录制记录修改优化变量的过程，得到相关的宏命令；然后使用ABAQUS对模型进行有限元分析，输出钳体受到的最大主应力和体积，然后将有限元分析得到的最大主应力代入预先编写的MATLAB程序中计算钳体的疲劳寿命；最后在ISIGHT中调用CATIA、ABAQUS和MATLAB对钳体进行轻量化分析；待优化完成后再对优化结果进行处理，若结果可行则可以根据轻量化结果试制产品，若结果不可行则寻找产生问题的原因，待问题解决后重新进行上述操作。

3.2ISIGHT集成CATIA、ABAQUS和MATLAB

图7所示为在ISIGHT中集成CATIA、ABAQUS和MATLAB的优化框架。使用Simcode组件通过批处理命令集成CATIA、ABAQUS、MATLAB和Delete模块。其中CATIA模块通过宏命令更改优化变量的值，并为有限元分析提供模型。ABAQUS模块通过python命令对更改后的模型进行有限元分析，并输出钳体的最大主应力和体积。MATLAB模块用于计算并输出钳体的疲劳寿命。Delete模块由自编程序组成，主要用于删除当前循环中产生的中间文件，以保证下一个循环的顺利执行。Calculator组件用于将ABAQUS模块中计算得到的最大主应力赋值给MATLAB中的相应变量。

图7　ISIGHT集成CATIA、ABAQUS和MATLAB的优化框架

3.3设置优化参数

钳体的优化变量为内侧凹槽的深度，如图2所示。选择凹槽的半径为优化变量，记为R。在Loop组件中设置R由131 mm变化到135 mm，增量为0.02 mm。优化目标为钳体的体积和疲劳寿命，将体积小且疲劳寿命高的解作为最优解。

3.4轻量化结果

优化完成后可以在ISIGHT的History菜单中以列表的形式查看优化结果，也可以在Graphs菜单下以图表的形式查看。图8～图10所示分别为在ISIGHT中优化得到的钳体的体积、应力和疲劳寿命随R变化的情况。

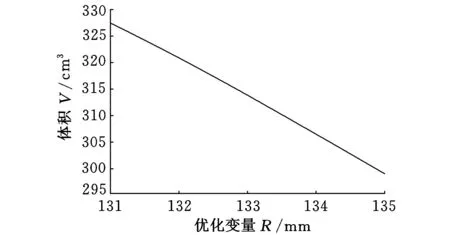
图8　体积随R的变化关系

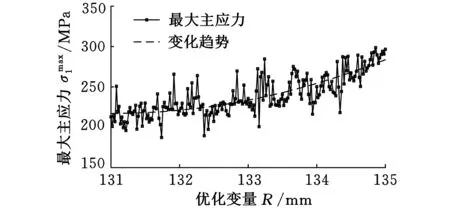
图9　最大主应力随R的变化关系

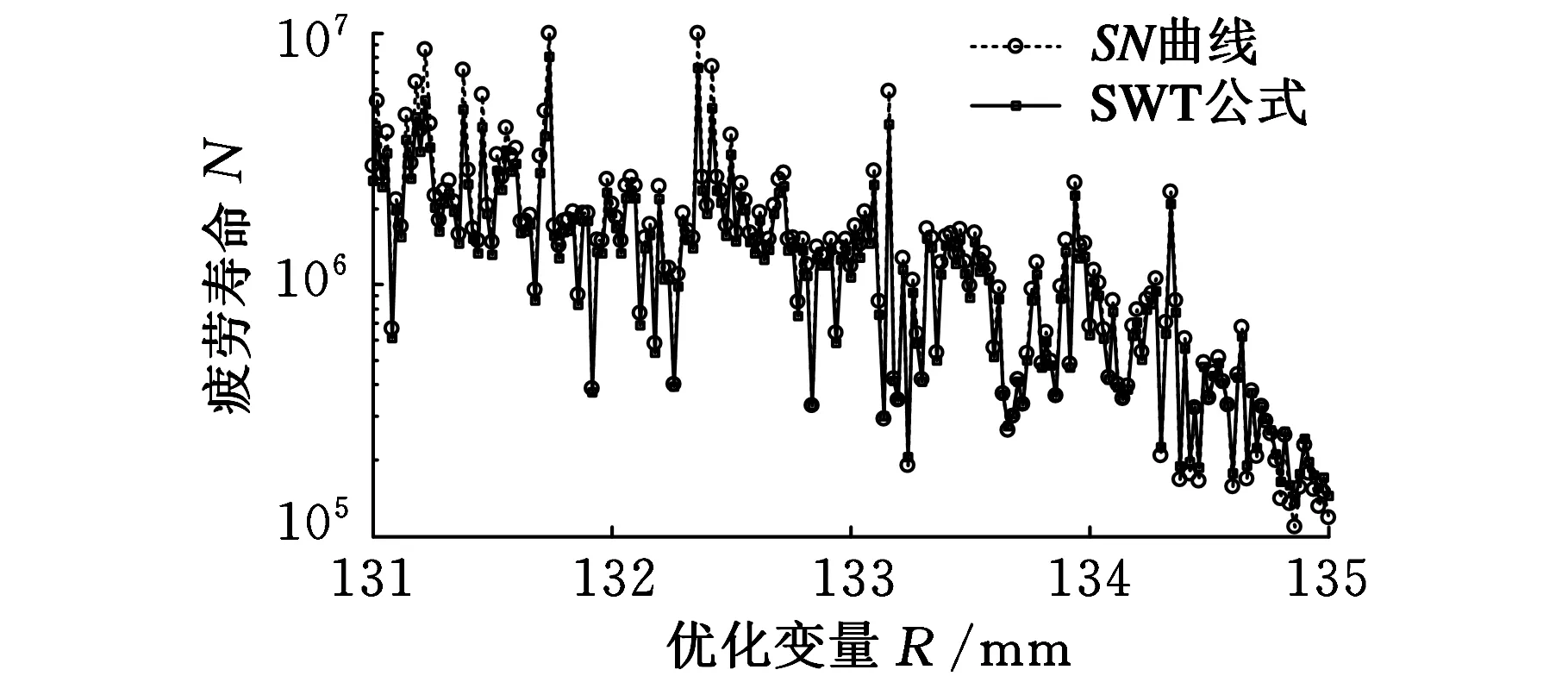
图10　疲劳寿命随R的变化关系

由图8可知，钳体的体积随着R的增加逐渐减小，由此说明通过改变R的值能对钳体实现轻量化，且R的值越大轻量化效果越明显。

图9表示的是优化过程中钳体上的最大主应力随R的变化情况。随着R的变化，最大主应力的值在一定范围内波动，但仍有逐渐增大的趋势，如图中虚线所示。这表明随着R的增加钳体上的最大主应力会逐渐增大。

图10所示为根据最大主应力计算得到的疲劳寿命随R的变化关系。本文根据材料的SN曲线和SWT公式两种方法计算得到钳体的疲劳寿命。由图10可见，两种方法计算得到的疲劳寿命大小较为接近。总体而言，根据SWT公式计算得到的疲劳寿命比根据SN曲线计算得到的疲劳寿命更为保守。因此，本文根据SWT公式计算得到的疲劳寿命来近似作为零件的疲劳寿命。

结合图8和图10选取R的最终优化尺寸为133.40 mm，优化前后钳体的体积和疲劳寿命如表3所示。由表3可以看出，通过优化，钳体的质量减小了5%，此时钳体仍具有较高的疲劳寿命。

表3　钳体轻量化结果

4　结论

(1)通过有限元分析得到制动过程中制动盘受到的制动力矩，并将其与实验测得的制动力矩进行比较，比较结果表明，有限元分析结果与真实情况一致性好。

(2)根据钳体的尺寸和表面质量对钳体材料的疲劳极限和SN曲线进行修正，结合修正后的SN曲线和SWT公式对钳体的疲劳寿命进行估算，根据优化结果，选择SWT公式计算结果作为钳体的疲劳寿命。

(3)建立了ISIGHT集成CATIA、ABAQUS和MATLAB的优化流程进行轻量化设计计算，设计计算结果表明：在保证钳体的疲劳寿命的同时使其质量减小了5%，在一定程度上实现了轻量化目标。

(4)本文仅对一个尺寸进行轻量化使钳体的质量减小了5%，可以对钳体零件进行综合分析确定出更多的优化变量，进一步减小其质量，本文方法同样适用于其他机械零件，对进行轻量化设计有参考价值。

[1]蔡运迪, 唐文献, 黄秋芸, 等. 水冷盘式制动器热疲劳失效有限元分析[J].中国机械工程, 2012, 23(22):2726-2731.

Cai Yundi, Tang Wenxian, Huang Qiuyun, et al. Finite Element Analysis(FEM) on Thermal Fatigue Failure of Water-cooling Disc Brake[J]. China Mechanical Engineering, 2012, 23(22):2726-2731

[2]Käsemann C P, Huart M, Stobbe F, et al. Mechanical Braking System for the Pulsed Power Supply System of ASDEX Upgrade[J]. Fusion Engineering and Design, 2013, 88(9): 1491-1494.

[3]Hohmann C, Schiffner K, Oerter K. Contact Analysis for Drum Brakes and Disk Brakes Using ADINA[J]. Computers & Structures, 1999, 72(1): 185-198.

[4]Liu P, Zheng H, Cai C. Analysis of Disc Brake Squeal Using the Complex Eigenvalue Method[J]. Applied Acoustics, 2007, 68(6): 603-615.

[5]Belhocine A, Bouchetara M. Thermal Analysis of a Solid Brake Disc[J]. Applied Thermal Engineering, 2012, 32: 59-67.

[6]Duraiselvam M, Valarmathi A, Shariff S M. Laser Surface Nitrided Ti-6Al-4V for Light Weight Automobile Disk Brake Rotor Application[J]. Wear, 2014, 309(1): 269-274.

[7]Kim J G, Jang G W. Development of a Lightweight Frame for a 40-foot Flatbed Trailer by Using CAE-based Structural Optimization[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2011, 225(5): 643-652.

[8]张勇, 李光耀, 王建华. 多目标遗传算法在整车轻量化优化设计中的应用研究[J]. 中国机械工程, 2009, 10(4): 500-503.

Zhang Yong, Li Guangyao, Wang Jianhua.Design Optimization on Lightweight of Full Vehicle Based on Muti -objective Genetic Algorithm[J]. China Mechanical Engineering, 2009, 10(4): 500-503.

[9]Jegadeeshwaran R, Sugumaran V. Comparative Study of Decision Tree Classifier and Best First Tree Classifier for Fault Diagnosis of Automobile Hydraulic Brake System Using Statistical Features[J]. Measurement, 2013, 46(9): 3247-3260.

[10]崔泗鹏, 姚卫星, 夏天翔. 连接件振动疲劳寿命分析的名义应力法[J]. 中国机械工程, 2014, 25(18): 2519-2522.

Cui Sipeng, Yao Weixing, Xia Tianxiang. Nominal Stress Approach for Fatigue Life Prediction of Mutifastener Joints under Vibration Loading[J]. China Mechanical Engineering, 2014, 25(18): 2519-2522.

[11]朱森第. 机械工程材料性能数据手册[M]. 北京: 机械工业出版社, 1994.

[12]秦大同, 谢里阳. 现代机械设计手册(第6卷)[M]. 北京: 化学工业出版社, 2011.

[13]赵少汴, 王忠保. 抗疲劳设计——方法与数据[M]. 北京: 机械工业出版社, 1997.

[15]Fajdiga G, Sraml M. Fatigue Crack Initiation and Propagation under Cyclic Contact Loading[J]. Engineering Fracture Mechanics, 2009, 76(9): 1320-1335.[16]Xia Z, Kujawski D, Ellyin F. Effect of Mean Stress and Ratcheting Strain on Fatigue Life of Steel[J]. International Journal of Fatigue, 1996, 18(5): 335-341.

(编辑郭伟)

Research on Lightweight Design for Disc Brake Caliper

Tang JinyuanZhao Guowei

State Key Labratory of High Performance Complex Manufacturing,Changsha,410083

Taking volume and fatigue life as lightweight design goal, an integrated computer-aided technology was used for disc brake caliper’s lightweight design. First, through comparing the barking torque which got by FEA and experiments it is proved that FEA’s steps and methods are correct and feasible. Then, combining the maximum principal stress which got by FEA with nominal stress method and Smith method was used to calculate the fatigue of caliper. Finally, Through ISIGHT integrating CATIA、ABAQUS and MATLAB, the lightweight of caliper was performed.

brake caliper; lightweight; finite element analysis(FEA); brake torque; fatigue life

2014-12-02

国家自然科学基金资助项目(51275530)

TP302DOI：10.3969/j.issn.1004-132X.2015.17.002

唐进元，男，1962年生。中南大学机电工程学院教授。研究方向为机械设计及理论。赵国伟，男，1989年生。中南大学机电工程学院硕士研究生。