基于改进PSO算法的数控机床主轴优化设计
朱成实 勾延生 李铁军 李尚帅
沈阳化工大学,沈阳,110142
基于改进PSO算法的数控机床主轴优化设计
朱成实勾延生李铁军李尚帅
沈阳化工大学,沈阳,110142
通过分析主轴结构和加工过程中受载变形情况, 建立了主轴优化设计的数学模型。根据邓克莱法计算得到的一阶固有频率近似值,引入动态约束条件 。针对传统优化设计方法在解决主轴优化设计中出现的问题,引入粒子群优化 (PSO) 算法,并提出了一种惯性权重值适应性递减的粒子群(ADW)算法。将ADW算法用于数控机床主轴优化实例中,得到主轴结构参数优化组合。研究结果表明,运用所建立的主轴优化设计数学模型及改进粒子群算法可以得到主轴结构参数优化组合,充分显示了该研究方法的有效性。
数控机床主轴;数学模型;粒子群算法;惯性权重;优化设计
0 引言
机床主轴是机床的重要部件,它直接参与机床加工,其性能直接影响生产率、表面粗糙度和加工精度,是决定机床性能的重要因素[1-3]。主轴的结构参数是影响主轴性能的关键指标,因而对主轴结构参数进行优化设计是十分必要的[4-5]。传统的优化设计方法存在求解过程复杂和寻优过程困难的问题[6],而粒子群算法是一种容易实现、调整参数不多且其本身没有复杂数学操作的优化算法[7-8]。本文采用一种新型的粒子群算法对主轴结构参数进行优化设计,使优化过程得到简化,取得了较好的效果。
1 改进粒子群算法
粒子群优化(particle swarm optimization,PSO)算法是由Kennedy等[9]在1995年基于鸟群觅食行为提出的一种随机优化算法。后来Shi等[10]引入惯性权重w来更好地平衡探索(exploration)和收敛(convergence),形成了现有的标准PSO算法。粒子群算法首先初始化一群随机粒子,然后通过迭代找到最优解。在每一次迭代中,粒子根据下式来更新自己的速度和位置:
vi,k+1=wvi,k+c1r1(pi-zi,k)+c2r2(pg-zi,k)
zi,k+1=zi+vi,k+1
其中,zi表示第i个粒子的位置,pi为粒子当前找到的个体最优位置;pg为整个种群当前找到的最优位置;k是当前迭代次数;r1和r2为[0,1]之间的随机数字;c1和c2被称作习因子。vmax和vmin是常数,用来限制速度。w是惯性权重,它决定了先前速度对当前速度的影响程度,因此可以平衡全局收敛能力和局部收敛能力的比例关系。现有算法中,Shi等[10]提出的惯性权重值线性递减(linearly decreasing weight,LDW)PSO算法在优化性能方面有显著的效果,但是这种惯性权重值w递减的策略也有其缺点:一方面,如果早期已找到全局最优点,则过大的权重值可能会使粒子跳出这个最优点,因此不能在其附近搜索,从而降低最优点的搜索能力;另一方面,如果在初期无法搜索到最优点,随着后期w的逐渐减小,算法的局部收敛能力加强,使算法容易陷入局部最优[11-13]。综上,本文提出一种惯性权重值适应性递减(adaptively decreasing weight,ADW)的粒子群算法,简称ADW算法。在该算法中,惯性权重值不仅随迭代次数的增加而递减,而且会随着粒子群进化而适应性改变。
为使惯性权重值在递减的同时具有适应性,引入进化率的概率[14]:个体最优值决定全局最优值的变化,同时也反映了粒子的运动效果,在迭代过程中,当前迭代的个体最优值总要优于或至少等于上次迭代的个体最优值。因此,可以比较当前迭代的个体最优值与上次迭代的个体最优值,从而判断粒子是否向全局最优位置进化。以寻找极小值问题为例,用s(i,k)判断粒子是否进化,即
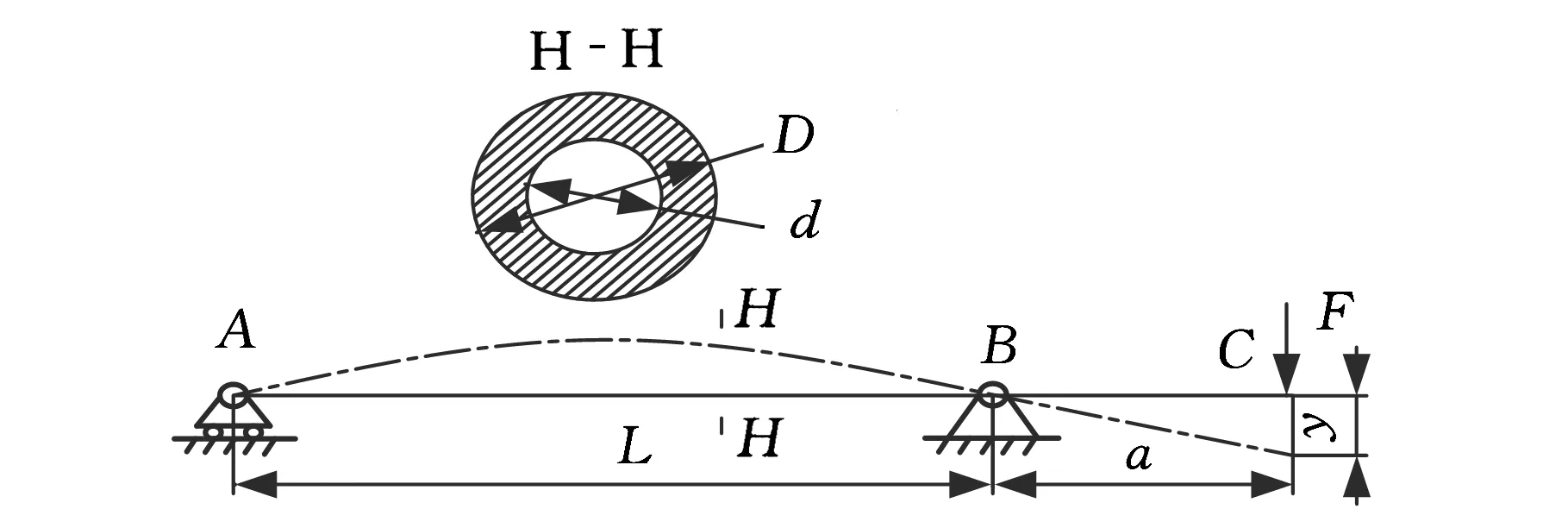
其中,pi,k表示到第k次迭代所找到的个体最优位置;F()为优化函数,当F(pi,k) 其中,npp为种群粒子个数,Ps(k)是[0,1]之间的一个值。较大的进化率值表示种群中大多数粒子发生进化,说明种群距全局最优位置较远,需要相对较大的速度去寻找最优位置;而较小的进化率值表明粒子群在全局最优位置附近,不需要较大的速度去搜索。 综上所述,可以通过进化率的大小来调节惯性权重值,使其在递减的同时具有适应性。惯性权重值w可表示为 其中,kmax是最大迭代次数。这样可以保证粒子具有较强的前期搜索能力和后期收敛能力,并有效避免了粒子早期跳出全局最优和后期陷入局部最优。 数控机床主轴一般为多支撑的空心阶梯轴,为便于使用材料力学公式进行结构分析,通常将阶梯轴简化为一当量直径表示的等截面轴。图1所示是一个已经简化的机床主轴。 图1 机床主轴变形简图 2.1确定设计变量 以主轴外直径D、内直径d和轴上各段长L作为设计变量。即 X=[d∑Di∑Li]T 2.2建立目标函数 以主轴体积最小和刚度最大为设计目标,其中刚度可用伸出端C点的挠度来表征。F1(x)为主轴挠度目标函数,F2(x)为主轴体积目标函数,则优化目标函数为 (1) 式中,λ1、λ2为加权因子,反映各分目标函数的重要程度;kA、kB分别为前后支承刚度,N/m;F为切削力;E为材料的弹性模量,Pa;I为主轴惯性矩,m4。 2.3约束条件 (1)强度约束。由于切削应力强度限制,建立强度约束:g1(x)=s-[τT]≤0。给定输入功率和转速的情况下,有 式中,D为主轴平均直径;P为主轴传递功率,kW;n为主轴转速,r/min;[τT]为主轴许用切削应力,Pa。 (2)挠度约束。由于主轴外伸端的挠度y不得超过许用值y0,建立刚度约束:g2(x)=y-y0≤0。即 式中,η为传动效率;v为主轴线速度。 (4)扭转变形约束。轴的扭转变形条件为φ≤[φ],建立扭转变形约束:g4(x)=φ-[φ]≤0。给定转矩时,φ=5.73×104T/(GIp),则 式中,T为主轴的工作转矩,N·m;G为剪切弹性模量,Pa;Ip为主轴极惯性矩,m4。 (5)转角约束。轴的偏转角θ应小于许用值[θ],建立转角约束:g5(x)=θ-[θ]≤0,给定外力时,θ=FaL/(2EI),则 式中,[θ]为许用偏转角,rad/m。 (6)动态性能约束。机床主轴具有一定静刚度要求的基础上,要保证主轴结构的动态特性。主要考虑主轴一阶固有频率f的约束,要求一阶固有频率不低于f0=1400 Hz,建立一阶固有频率约束:g6(x)=f0-f≤0,由邓克莱法[15]计算可得到一阶固有频率近似值f,则 g6(x)=1400- 式中,g为重力加速度;m为图1中主轴AB段的质量。 (7)设计变量边界约束。由主轴各边界尺寸,建立主轴尺寸边界约束: 2.4基于粒子群算法构造适应度函数 根据优化目标函数及约束条件,可将问题转化为在满足gj(x)≤0(i=1,2,…,n)条件下求可行域内目标函数F(x)的极小值问题。采用罚函数法,实现约束优化问题向无约束优化问题转化,则适应度函数fitness(x)=F(x)+p(x),其中,p(x)为惩罚函数。采用动态罚函数法得到数控机床主轴的适应度函数: 其中,通常取c=0.5,α=β=2。 3.1优化设计实例 以沈阳机床集团生产的SSCK40-750型机床主轴部件为例,进行基于ADW算法的机床主轴优化设计。最低转速nmin=30 r/min,主电机功率P=7.5 kW,转矩T=700 kN·mm,切削力F=3500 N,弹性模量E=160 GPa,剪切弹性模量G=80 GPa,密度ρ=7.4×10-6kg/mm3。该机床主轴结构如图2所示。 图2 主轴结构简图 由式(1),主轴的优化设计变量为 X=[dD1D2D3D4D6L1L2…L5]T 构造适应度函数: fitness(x)=F(x)+p(x)= 其中,gj(x)为约束函数。且L=L4+L5,a=L1+L2+L3。 3.2结果分析 为了证明ADW算法的有效性,分别采用ADW算法和LDW算法对主轴适应度函数进行优化。主轴设计变量有11个,取粒子维数为11,每一维的范围根据约束条件确定,种群粒子个数为20,最大迭代次数为300,c1=1.8,c2=1.8,wmax=0.9,wmin=0.4,vmax=1,vmin=-1,λ1=0.8,λ2=0.2,得到优化曲线如图3所示。 图3 优化过程图 由图3可知:ADW算法在收敛速度方面要优于LDW算法,ADW算法经过12次迭代后收敛,而LDW算法则经过25次迭代后收敛。在收敛精度方面,ADW算法也找到了较LDW算法更优的主轴适应度函数值。优化结果见表1。 对表1中优化前后的主轴参数数据进行分析比较: (1)LDW算法结构参数优化结果为 L=L4+L5=291 mm 主轴刚度提高率为 主轴体积减小率为 (2)ADW算法结构参数优化结果为 L=L4+L5=292 mm a=L1+L2+L3=135 mm 主轴刚度提高率为 主轴体积减小率为 从分析结果中可得:在主轴体积优化方面,ADW算法得到的主轴结构参数使得主轴体积较原有体积减小9.7%,而LDW算法使得主轴体积减小8.4%,优化结果相差1.3%,因此,ADW算法优化效果要优于LDW算法。在主轴刚度方面,ADW算法得到的主轴结构参数使主轴刚度较原有刚度提高3.5%,而LDW算法使主轴刚度提高2.9%,优化结果相差0.6%。 (1)本文提出了一种适应性递减的新型粒子群算法,引入Ps来衡量种群粒子的进化度,并将其作为惯性权重w的变量,使w具有适应性递减的特性,从而改进算法性能,与LDW算法相比,ADW算法在收敛速度和收敛精度方面都体现了较好的效果。 (2)建立了主轴优化数学模型,以主轴刚度和体积为优化目标,在约束条件中,考虑动态约束条件——固有频率的影响,同时引入强度约束、挠度约束、切削力约束、扭转变形约束、转角约束、设计变量边界约束,使用邓克莱法计算得到主轴一阶固有频率的近似值,加入动态性能约束,从而实现数控机床主轴优化数学模型的表达。 (3)主轴优化设计实例分析结果表明,应用ADW算法对主轴进行优化,能够保证优化进程收敛,并且优化效果明显,其中主轴刚度提高9.7%,主轴体积减小3.5%。 [1]Wang Min,Zhang Xinyun,Zan Tao,et al. Investigation of Static and Dynamic Characteristics of a High-speed Electric Spindle Based on ANSYS[J].Journal of Beijing University of Technology,2012,38(7):988-991. [2]Gao Shanghan,Meng Guang.Adwances in Research on Dynam IC Characteristics of Machine Tool Spindle[J].Journal of Vibration and Shock,2007,26(6):103-109. [3]Zhang Bo,Hu Endian,Chen Tianning,et al.Dynamic Optimum Design on Spindle Components of Numerical Controlled Machine Tools[J].Journal of Machine Design,2004,21(5):33-35. [4]Gupta S,Tiwari R,Nair S B.Multiojective Design Optimization of Rolling Bearings Using Genetic Algorithms[J].Mechanism and Machine Theory,2007,42(10):1418-1443. [5]Chakraborthy I, Vinay K, Nair S B.Rolling Element Bearing Design through Genetic Algorithms [J].Engineering Optimization, 2003, 35( 6):649-659.[6]JiangT,Chirehdast M.A System Approach to Structural Topology Optimization[J].Designing Optimal Connections,1999,30: 521-523. [7]Eberhart R C,Shi Y H.Particle Swarm Optimization:Developments,Applications and Resources[C]//Proceedings of the IEEE Congress on Evolutionary Computation.Piscataway: IEEE Service Center,2001:81-86. [8]Yan Zheoing, Deng Chao, Zhao Yufei,et al.Application of Improved Particles Swarm Algorithm to UUV 3-D Path Planning[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition),2013,41(12):64-68. [9]Kennedy J,Eberhart R C.Particle Swarm Optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks.Piscataway:IEEE,1995:1942-1948. [10]Shi Y H,Eberhart R C.A Modified Particle Swarm Optimizer[C]//Proceedings of the IEEE Congress on Evolutionary Computation.Piscataway:IEEE Service Center,1998:69-73. [11]Zhang Xuanping, Du Yuping, Qin Guoqiang,et al.Adaptive Particle Swarm Algorithm with Dynamically Changing Inertia Weight[J]. Journal of Xi'an Jiaotong University,2005,39(10):1039-1042. [12]Hu Jianxiu,Zen Jianchao.A Particle Swarm Optimization Model with Stochastic Inertia Weight[J].Computer Simulation,2006,23(8):164-167. [13]Liu Jianjua, Fan Xiaopin, Zhai Zhihua. New Particle Swarm Optimization Algorithm with Dynamic Change of Inertia Weights[J].Computer Engineering and Applications, 2007, 43(7):68-70. [14]Nickabadi F,Ebadzadeh M M,Safabakhsh R.A Novel Particle Swarm Optimization Algorithm with Adaptive Inertia Weight[J].Applied Soft Computing,2011,11:3658-3670. [15]Singiresu S.Rao.机械振动[M].北京:清华大学出版社,2009. (编辑陈勇) Optimization Design of CNC Machine Tool Spindle Based on Improved PSO Algorithm Zhu ChengshiGou YanshengLi TiejunLi Shangshuai Shenyang University of Chemical Technology,Shenyang,110142 A mathematical model of CNC machine tool spindle optimization design was established by analyzing the spindle’s structure and the deformation under load under the working situations.A dynamic constraint was applied according to approximate value of first natural frequency calculated by Dunkerley.The PSO algorithm was applied to solve the problems of the traditional optimization design and a particle swarm algorithm with adaptively decreasing inertia weight(ADW) was presented.ADW algorithm was used to the example of CNC machine tool spindle’s optimization. The results show that the spindle structure parameter optimization can get from the mathematical model of CNC machine tool spindle optimization design and the improved PSO algorithm,the effectiveness of this method is demonstrated. CNC machine tool spindle;mathematical model;particle swarm optimization(PSO) algorithm;inertia weight;optimization design 2015-01-16 国家自然科学基金资助项目(51375081) TH133.2DOI:10.3969/j.issn.1004-132X.2015.20.015 朱成实,男,1962年生。沈阳化工大学工业与艺术设计系教授。研究方向为机械优化设计、机械设备智能故障诊断。发表论文30篇。勾延生,男,1990年生。沈阳化工大学机械工程学院硕士研究生。李铁军,男,1978年生。沈阳化工大学机械工程学院讲师。李尚帅,男,1990年生。沈阳化工大学机械工程学院硕士研究生。2 机床主轴优化数学模型的建立
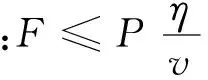
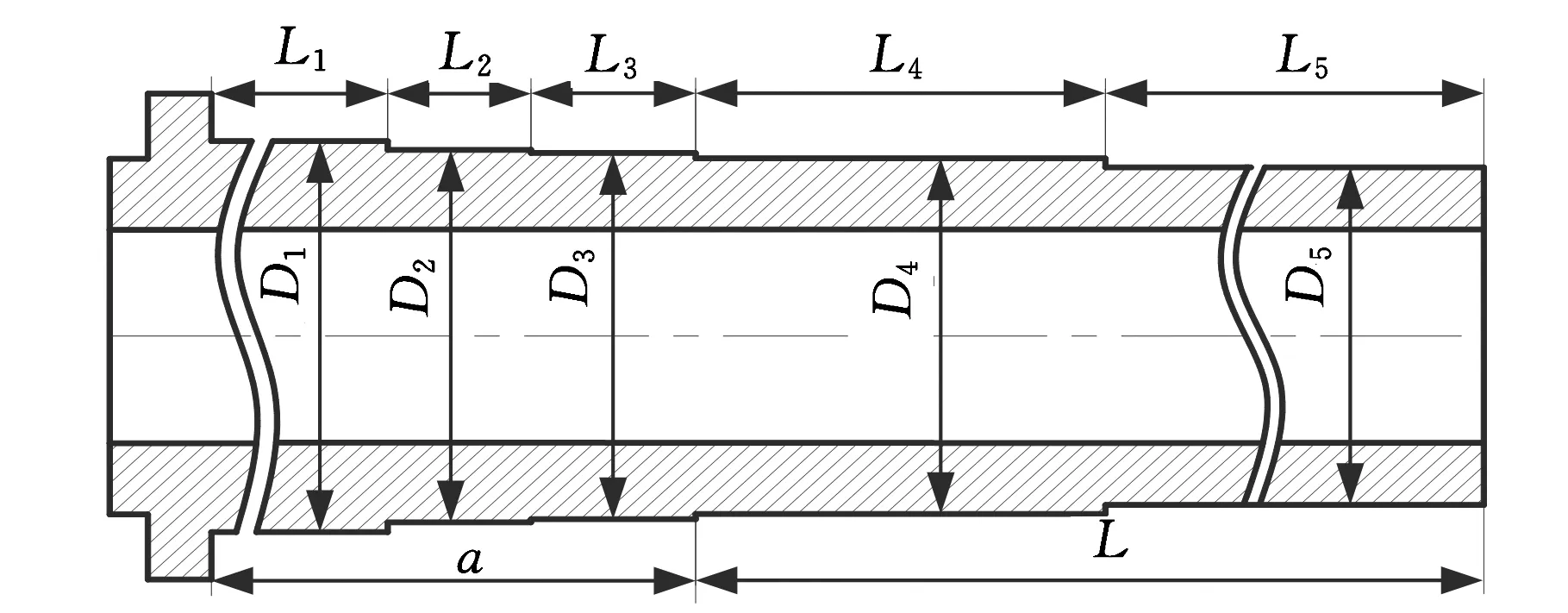
3 主轴优化设计实现


4 结论

