融合小波分解与时频分析的单通道振动信号盲分离方法

孟　宗　王晓燕　马　钊

1.河北省测试计量技术及仪器重点实验室(燕山大学),秦皇岛,066004 2.国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,066004

融合小波分解与时频分析的单通道振动信号盲分离方法

孟宗1,2王晓燕1马钊1

1.河北省测试计量技术及仪器重点实验室(燕山大学),秦皇岛,066004 2.国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,066004

针对单通道振动信号盲源分离是一个病态问题，且传统的振动信号盲源分离方法往往忽略信号的非平稳性的问题,提出了一种融合小波分解与时频分析的单通道振动信号盲源分离方法。首先利用小波分解与重构将单通道信号转化为多通道信号，解决了盲源分离的欠定问题;然后利用基于时频分析的盲源分离算法分析非平稳信号，得到源信号的估计信号,实现了非平稳信号盲源分离。仿真和实验结果表明，该方法可以有效地解决单通道非平稳振动信号的盲源分离问题。

盲源分离；小波分解；时频分析；故障诊断

0　引言

盲源分离(blind source separation,BSS)[1]对源信号的先验知识要求很少，但是盲源分离要满足一些基本条件，如源信号数不多于观测信号数，源信号是非高斯、平稳且相互统计独立的。在实际中,通常希望用较少的传感器获得更多的设备状态信息，因此，欠定的盲源分离甚至单通道混合信号的盲源分离普遍存在于机械故障诊断中。申永军等[2]通过Gabor变换与逆变换,实现了混合信号升维,进而实现正定盲源分离;毋文峰等[3]针对单通道问题，提出了基于经验模式分解的盲源分离方法;李志农等[4]结合局域均值分解和盲源分离的特点,提出了一种基于局域均值分解的欠定盲源分离方法;李晓晖等[5]针对一维观测矩阵的极度欠定盲源分离模型，利用总体经验模式分解的优势解决了欠定的盲源分离问题。

实际机械设备中，振动信号往往表现为非平稳的，有必要借助时频分析(time-frequency analysis,TFA)的优点,将盲源分离拓展到时频域[6-9]。针对这种机械振动信号具有欠定性,且不能忽略信号的非平稳性的盲源分离情况,本文提出了融合小波分解与时频分析的单通道盲源分离方法。该方法利用小波分解与重构实现信号的升维，重构观测信号;对重构后的观测信号进行基于时频分析的盲源分离,得到了源信号的估计信号。

1　基于时频分析的盲源分离

考虑到机械故障信号的非平稳性，其频谱特性是随时间而变化的，而时频分析是分析非平稳信号的重要工具[10]。本文充分利用时频分析和盲源分离的优点[11],对机械振动信号进行分离处理。基于时频分析的盲源分离主要包括以下两部分。

(1)对观测信号进行白化处理。考虑无噪声干扰的瞬时混合的盲源分离问题，m维观测向量x(t)为

x(t)=As(t)

(1)

x(t)=(x1(t),x2(t),…,xm(t))T

s(t)=(s1(t),s2(t),…,sn(t))T

其中,s(t)是n维未知的相互独立源信号,且m≥n；A是一个未知的混合矩阵。

定义观测信号x(t)的自相关矩阵为

Rx=E[x(t)x(t)*]

其中,上标*表示复共轭,对Rx进行特征值分解得到其特征值和相应的特征向量，n个最大的特征值和相应的特征向量分别用λ1,λ2,…,λn和h1,h2,…,hn表示。假设受到的干扰为白噪声，则噪声方差σ2的估计是Rx的m-n个最小特征值的平均值。白化信号z(t)=(z1(t),z2(t),…,zn(t))T可由下式得到：

i=1,2,…,n

白化矩阵W为

W=[(λ1-σ2)-1/2h1(λ2-σ2)-1/2h2…

(λn-σ2)-1/2hn]H

其中，上标H表示复共轭转置。对式(1)左乘一个白化矩阵W，得到白化后的观测信号：

z(t)=Wx(t)=WAs(t)=Us(t)

(2)

由式(2)可以看出,白化信号是源信号的一个“酉矩阵混合”。

(2)矩阵联合对角化。同时对式(1)左右两端进行时频变换,得到源信号与观测信号的时频分布矩阵的关系：

Dxx(t,f)=ADss(t,f)AH

其中,Dss(t,f)为源信号的时频分布;Dxx(t,f)为观测信号的时频分布。将Dxx(t,f)左右分别乘以W,得到白化的时频分布矩阵：

Dzz(t,f)=WADss(t,f)AHWH=UDss(t,f)UH

得到白化矩阵W和酉矩阵U后,则源信号的估计信号为

(3)

其中,时频分析采用平滑伪Wigner-Ville分布。

2　融合小波分解与时频分析的单通道盲源分离

对单通道振动观测信号进行小波分解与重构，使得盲源分离的观测信号数目大于或等于源信号数目，满足盲源分离的基本假设条件。结合小波分解与基于时频分析的盲源分离方法，不仅可以处理欠定的振动信号，而且可以有效地分析非平稳信号。单通道信号盲源分离的分离过程如图1所示。

图1　单通道盲源分离过程

具体分解步骤如下：

(1)x(t)是从传感器获得的单通道观测信号,对x(t)进行小波分解,得到小波分解的低频系数cA1与高频系数cD1。

(2)利用小波系数进行信号的重构，得到新的多维观测信号x,xi,0,xi,1,xi-1,1,…,xi-n+1,1。

(3)对新的多维观测信号进行奇异值分解，利用贝叶斯准则进行源数估计，得到源信号的数目。

(4)从新的观测信号中选取与源信号数目相同的维数的观测信号,构成新的观测信号。

(5)对观测信号进行白化处理，得到白化矩阵W以及白化后的观测信号。

(6)计算白化后数据的时频分布,采用平滑伪Wigner-Ville分布。

(7)联合对角化时频分布,得到酉矩阵U。

(8)根据式(3)估计出源信号。

3　仿真

旋转机械有两个至关重要的组成部分，即轴承和齿轮。当轴承发生故障时，因为受力不均匀会引发振动信号的幅值调制；齿轮是用来传递力的，当齿轮发生故障时，由于承载的不对称性，将会出现啮合频率调制现象。轴承和齿轮的振动信号可分别对应信号的调幅、调频现象。融合小波分解与时频分析的盲源分离方法将欠定盲源分离转化为正定盲源分离，再利用时频分析的优势，充分描述了非平稳信号。对于非平稳信号的欠定盲源分离问题,该方法可以很好地分离出估计源信号。据此仿真3个振动源信号s1、s2、s3：

其中,f1=100 Hz,f2=150 Hz,f3=180 Hz,f4=500 Hz,f5=1000 Hz,仿真获得相应的3个源信号的波形,如图2所示。

(a)源信号1波形

(b)源信号2波形

(c)源信号3波形图2　源信号时域波形

取随机混合矩阵

根据式(1),采用线性混合的方法，将这3个源信号混合后得到两个混合信号。为了验证本文方法可以有效地解决单通道盲源分离问题，假设在盲源分离应用中，由于监测条件的限制，仅仅监测到了一路观测信号，所以从两个混合信号中选取一个，其波形图见图3，将选取的图3所示的信号作为实验的单通道观测信号,对其进行分析、验证。

图3　单通道混合信号时域波形

利用小波分解方法对该单通道混合信号进行分解，得到一系列不同频率的子带信号，从中选择2个信号与原混合信号构成新的观测信号，如图4所示，使得观测信号的数目与源信号的数目相同(均为3个),从而使得盲源分离的问题由欠定转换为正定。

(a)新观测信号1波形

(b)新观测信号2波形

(c)新观测信号3波形图4　新观测信号时域波形

采用传统的盲源分离方法对新的观测信号进行分离，如JADE算法，得到的分离结果如图5所示。对比图5与图2可以看出，JADE分离的3个估计信号与源信号的排列顺序发生了变化，每个源信号相对应的估计信号的波形不平滑，有毛刺并且有明显的变形，显然，传统JADE算法分离得到的估计信号效果很不理想。

(a)估计信号1波形

(b)估计信号2波形

(c)估计信号3波形图5　JADE分离估计信号

对于非平稳信号，其频谱特性是随着时间变化而变化的，而时频分析为分析非平稳信号提供了有力的工具，将时频分析与盲源分离相结合，利用各自的优点进行分离。对新的观测信号进行平滑伪Wigner-Ville变换，得到相应的时频分布，如图6所示。

(a)新观测信号1时频分布

(b)新观测信号2时频分布

(c)新观测信号3时频分布图6　观测信号的时频分布

(a)新观测信号1分离结果

(b)新观测信号2分离结果

(c)新观测信号3分离结果图7　TFA-BSS方法分离结果

从图6可以清楚地看到每个观测信号中相应的归一化频率。对于非平稳振动信号,采用传统的盲源分离方法得不到很好的分离效果。所以,采用基于时频分析的盲源分离(TFA-BSS)方法对上述新的观测信号进行分离，分离结果如图7所示。对比图2和图7可知，源信号得到了很好的恢复，波形也得到了很好的保持。

对比不同的分离方法得到的结果，利用相似系数作为评价分离指标,结果见表1。表1中,si表示源信号,yi表示估计源信号,i=1,2,3。相似系数越接近1,则分离效果越好,从表1可发现,小波分解满足盲源分离的正定条件后,采用基于时频分析的盲源分离算法比直接使用JADE算法得到的分离结果效果更好。

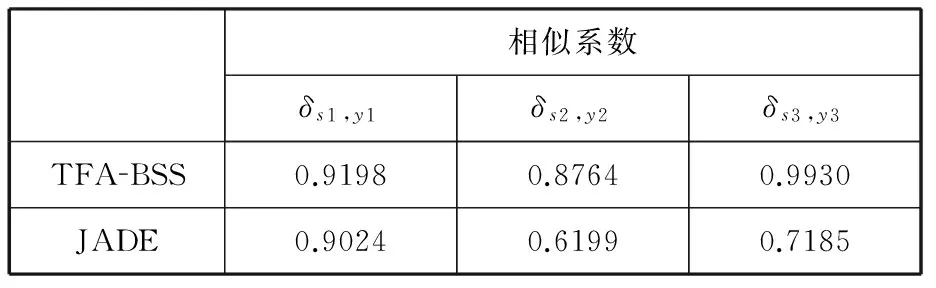
表1　分离结果评价指标

4　实验

实验以美国西储大学的滚动轴承点蚀故障数据为研究对象。在轴承故障实验中，使用电火花加工技术在轴承内圈、外圈上均布置了单点故障。电机转速为1797 r/min,故障直径为0.1778 mm,滚珠个数是9,振动信号的采样频率为12 kHz。

轴承出现内圈故障或外圈故障时，滚动体每次通过故障点都会产生一个周期性的冲击信号，内圈故障频率为

外圈故障频率为

式中,r为电机转速;m为滚珠个数；d为滚动体直径,d=7.9 mm；D为轴承节径,D=39 mm;α为接触角,α=0。

经计算可得,轴承的内圈故障频率理论值为162.1 Hz,轴承的外圈故障频率理论值为107.5 Hz。为了验证本文方法的有效性和可行性,将实验中的内圈故障信号和外圈故障信号通过一个2×2矩阵混合,得到两路混合观测信号，选择其中一路信号作为单通道观测信号,信号时域波形如图8所示。

图8　单通道观测信号

采用本文方法,首先对单通道信号进行进行小波分解，使观测信号升维，重构得到新的观测信号，满足了盲源分离的正定条件;然后利用TFA-BSS方法对重构后的观测信号进行盲源分离,得到了盲源分离的估计信号的时域波形，如图9所示。

(a)分离信号1时域图

(b)分离信号2时域图图9　分离信号时域图

仅从时域图中并不能确定轴承的故障类型。进一步对估计的源信号进行频域分析，其包络谱如图10所示。

(a)分离信号1包络谱图

(b)分离信号2包络谱图图10　分离信号包络谱图

由图10可以看出,其中第一个包络谱图在105.5 Hz和210.9 Hz处分别出现了峰值,而轴承外圈故障频率的理论值为107.5 Hz,105.5 Hz与理论值107.5 Hz非常接近，210.9 Hz明显是对应二倍频处，有细微的波动，可能是因为实际环境中客观因素的影响，但是仍然可以断定105.5 Hz对应着轴承的外圈故障特征频率。图10中第二个包络谱图在164.1 Hz出现了峰值，而轴承内圈故障频率的理论值为162.1 Hz,164.1 Hz与理论值162.1 Hz非常接近,可能是因为电机转速无法恒定在1797 r/min，而是在1797 r/min附近波动,可以断定164.1 Hz对应着轴承的内圈故障特征频率。因此,可以初步判定,观测信号中混合有轴承内圈故障信号和外圈故障信号。

5　结语

针对实际机械故障诊断中，由于条件限制，源信号的数目往往大于传感器的数目，传统的盲源分离方法无法实现有效分离的难题，本文将小波分解与基于时频分析的盲源分离方法相结合，通过小波分解与重构，实现观测信号的升维，使观测信号数大于或等于源信号数，从而实现信号盲源分离，进一步将该方法应用于单通道的振动信号的盲源分离中，通过仿真和实验研究结果验证了该方法的有效性和可行性。实际机械故障中源信号的幅值和频率都是随时间变化的，是非平稳的，如果忽略非平稳性，则盲源分离效果极差，本文结合时频分析与盲源分离的优点，实现了非平稳信号的有效盲源分离。

[1]Jutten C,Herault J.lind Separation of Source Part I:an Adaptive Algorithm Based on Neuromimetic Architecture[J].Signal Processing,1991,24:1-10.

[2]申永军,张光明,杨绍普,等.基于Gabor变换的欠定盲信号分离新方法[J].振动、测试与诊断,2011,31(3):309-313.

Shen Yongjun,Zhang Guangming,Yang Shaopu,et al.New Method for Blind Source Separation in Under-determined Mixtures Based on Gabor Transform[J].Journal of Vibration, Measurement & Diagnosis,2011,31(3):309-313.

[3]毋文峰,陈小虎,苏勋家.基于经验模式分解的单通道机械信号盲分离[J].机械工程学报,2011,47 (4)：12-16.

Wu Wenfeng,Chen Xiaohu,Su Xunjia.Blind Source Separation of Single-channel Mechanical Signal Based on Empirical Mode Decomposition[J].Journal of Mechanical Engineering,2011,47(4):12-16.

[4]李志农,刘卫兵,易小兵.基于局域均值分解的机械故障欠定盲源分离新方法[J].机械工程学报,2011,47(7):97-102.

Li Zhinong,Liu Weibing,Yi Xiaobing.Underdetermined Blind Source Separation Method of Machine Faults Based on Local Mean Decomposition[J].Journal of Mechanical Engineering,2011,47(7):97-102.

[5]李晓晖,傅攀.基于EEMD的单通道盲源分离在轴承故障诊断中的应用[J].中国机械工程,2014,25(7):924-930.

Li Xiaohui,Fu Pan.Application of Signal-channel Blind Source Separation Based on EEMD in Bearing Fault Diagnosis[J].China Mechanical Engineering,2014,25(7):924-930.

[6]陈建国,王奉涛,朱泓,等.改进ICA与HHT在转子故障诊断上的应用[J].中国机械工程,2009,20(17):2059-2062.

Chen Jianguo,Wang Fengtao,Zhu Hong,et al.Application of Improved ICA & HHT in Fault Diagnosis of Rotors[J].China Mechanical Engineering,2009,20(17):2059-2062.

[7]李强,付聪,江虹,等.融合经验模态分解与时频分析的单通道振动信号分离研究[J].振动与冲击,2013,32(5):122-126.

Li Qiang,Fu Cong,Jiang Hong,et al.Single-channel Vibration Signal Separation by Combining Empirical Mode Decomposition with Time-frequency Analysis[J].Journal of Vibration and Shock,2013,32(5):122-126.

[8]吴强,孔凡让,何清波,等.基于小波变换和ICA的滚动轴承早期故障诊断[J].中国机械工程,2012,23(7):835-840.

Wu Qiang,Kong Fanrang,He Qingbo,et al.Early Fault Diagnosis of Rolling Element Bearings Based on Wavelet Transform and Independent Component Analysis[J].China Mechanical Engineering,2012,23(7):835-840.

[9]张俊红,李林洁,马文朋,等.EMD-ICA联合降噪在滚动轴承故障诊断中的应用[J].中国机械工程,2013,24(11):1468-1472.

Zhang Junhong,Li Linjie,Ma Wenpeng,et al.Application of EMD-ICA to Fault Diagnosis of Rolling Bearings[J].China Mechanical Engineering,2013,24(11):1468-1472.

[10]向玲,唐贵基,胡爱军.旋转机械非平稳振动信号的时频分析比较[J].振动与冲击,2010,29(2):42-45.Xiang Ling,Tang Guiji,Hu Aijun.Vibration Signal’S Time-frequency Analysis and Comparison for a Rotating Machinery[J].Journal of Vibration and Shock,2010,29(2):42-45.

[11]绍忍平,曹精明,李永龙.基于EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断[J].振动与冲击,2012, 31(8):96-101.

Shao Renping,Cao Jingming,Li Yonglong.Gear Fault Pattern Identification and Diagnosis Using Time-frequency Analysis and Wavelet Threshold Denoising Based on EMD[J].Journal of Vibration and Shock,2012,31(8):96-101.

(编辑陈勇)

Single-channel Vibration Signal Separation by Combining Wavelet Decomposition with Time-frequency Analysis

Meng Zong1,2Wang Xiaoyan1Ma Zhao1

1.Key Laboratory of Measurement Technology and Instrumentation of Hebei Province(Yanshan University),Qinhuangdao,Hebei,066004 2.National Engineering Research Center for Equipment and Technology of Cold Rolling Strip,Qinhuangdao,Hebei,066004

Single-channel mechanical vibration signal-separation is an ill-conditioned problem,and in traditional methods, the blind source separation of vibration signals often ignores the nonstationarity.For this reason,a method on single-channel vibration signal separation was proposed based on wavelet decomposition and TFA.The method firstly used wavelet decomposition and reconstruction to make the single-channel signals into multi-channel signals,solving the problem of underdetermined blind source separation;Secondly,based on time-frequency analysis BSS was used to effectively analyze the non-stationary signals,then the estimation source signals were obtained,achieving blind source separation of non-stationary signals.Simulation and experimental results vertify the effectiveness of this method, and show the method can solve the problem of BSS of nonstationary single-channel vibration signals.

blind source separation(BSS);wavelet decomposition;time-frequency analysis(TFA);fault diagnosis

2014-09-28

国家自然科学基金资助项目(51575472,51105323);河北省自然科学基金资助项目(E2015203356);河北省高等学校科学研究计划重点资助项目(ZD2015049)

TN911.7DOI：10.3969/j.issn.1004-132X.2015.20.010

孟宗,男，1977年生。燕山大学电气工程学院教授、博士。主要研究方向为机械设备监测与故障诊断、动力学建模、信号检测与处理等。王晓燕，女，1988年生。燕山大学电气工程学院硕士研究生。马钊，男，1989年出生。燕山大学电气工程学院硕士研究生。