三维顶板斜向驱动方腔流有限元并行计算

王吉飞，万德成

(1. 上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室，上海 200240； 2. 高新船舶与深海开发装备协同创新中心，上海 200240)

三维顶板斜向驱动方腔流有限元并行计算

王吉飞1,2，万德成1,2

(1. 上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室，上海 200240； 2. 高新船舶与深海开发装备协同创新中心，上海 200240)

基于PETScFEM开源代码，采用分步有限元算法和区域分解法，并行计算了不同雷诺数下的三维顶板斜向驱动方腔流问题。计算结果表明，当顶板沿其对角线方向运动时，流体与下游侧壁发生斜向碰撞后在下游对角处汇聚并形成射流，该射流在与底面、上游侧壁碰撞后形成较为复杂的涡流结构。雷诺数大小对三维顶板斜向驱动方腔流的涡流场结构形态具有重要影响。并行性能分析表明区域分解法能有效地提高三维粘性方腔流的计算速度。

三维方腔流；斜向角；有限元；区域分解；并行计算

顶板驱动方腔流可模拟由某一壁面运动或外部流场运动所引起的方腔内部环流。这类流动在航空、环境、工业、交通运输、海洋工程等领域广泛存在，研究其流动特性具有重要的工程应用价值。Aidun 等[1]指出顶板驱动方腔流在涂镀和熔纺等工业装置中起到重要的作用。在液压管路运输中，适当部位设置一个较大的方腔可减少或吸收液压泵的压力和流量脉动对系统的影响，防止或减少液压冲击现象的发生。在航空领域，前缘缝翼、后缘缝翼、起落架箱和钉状洞穴等所形成的方腔流动是机身噪音的重要来源。在潜艇噪声中，弦外孔和排水孔等所产生的内部环流也是其水动力噪声的来源之一。研究方腔流对流动机理的探讨也有非常重要的意义，因为其简单的设置能展示几乎所有重要的流体力学现象，如角涡、展向涡、分叉、转捩、湍流等。方腔流模型的简单性使得其结果的分析和比较更容易，同时极易扩展到全雷诺数范围。

随着实验技术和计算机性能的不断提高，人们对三维顶板驱动方腔流进行了越来越多的研究，其中对顶板沿平行于侧壁方向运动引起的方腔流研究得最为广泛。Prasad和Koseff[2]对顶板驱动方腔流进行了开拓性的实验研究。Jiang等[3]，Wong等[4]以及其他学者对中、低雷诺数下的方腔流进行了数值模拟，Leriche等[5]，Hachem等[6]，Zang等[7]对高雷诺数的方腔流进行了数值模拟等。此外，Shankar等[8]对方腔流的研究进展做了很好的总结。

但在现实情况中，顶板运动方向或外部流场方向并不一定平行于方腔侧壁方向，而是与其有一定偏角。该偏角的存在使得方腔内部涡流场结构发生重大变化。研究顶板斜向驱动方腔流具有工程实用价值，能更好地防止或减少管路输运中的液压冲击现象，更好地降低飞机机身或潜艇噪声等，同时对流动机理的探讨也有重要的意义。国内外学者对顶板斜向驱动方腔流的研究较少，主要集中在飞机机身降噪方面。Disimile等、Czech等分别对飞机着陆装置(可简化为顶板驱动方腔流)的噪声进行了实验研究，结果表明当外部流方向与方腔侧壁成一定偏角时，不管流动是否振荡，方腔中均存在较强的声学压力。Pocitsky[9]基于商业软件Fluent研究了顶板沿其对角线方向运动所引起的方腔流，其雷诺数包括100，400，700，2 000和40 000，结果显示顶板斜向驱动方腔流具有更复杂的涡流结构。为了便于与前人的数值计算结果进行比较，本文着重研究顶板沿其对角线方向运动所引起的方腔流。

根据控制方程的离散方式不同，计算流体力学数值离散方法大体上可分为三个分支[10]：有限差分法、有限体积法和有限元法。相比于其他方法，有限元方法具有如下特点和优势[11,12]：1)有限元法具有理论完整可靠，形式单纯、规范，程序标准化，精度和收敛性得到保证等优点；2)相比于有限差分法，有限元法对于求解区域的单元剖分没有特别的限制，因此特别适合处理具有复杂边界流场的区域；3)相比于有限体积法，有限元法可以通过提高单元插值多项式的次数来提高解的精度，且对单元正则性要求不高。基于此，本文采用有限元法对不可压粘性流场进行数值模拟。

在对不可压粘性流体进行有限元分析时，速度和压力插值空间函数需满足inf-sup相容性条件，如不满足，则可能产生虚假的压力振荡。为解决压力稳定性问题，学者们相继提出了不同的方法，如速度和压力的不同阶插值，罚函数法，附加压力稳定项等方法。由Chorin等和Temam等提出的基于POISSON投影的分步算法则可采用无需满足相容性条件的速度压力插值空间函数。Guermond等[13]进一步验证，当速度和压力采用同阶插值函数时，只有在时间步长不太小时才能得到稳定的压力场。Codina等[14]得到了类似的结论，并进一步提出了具有压力稳定性的分步算法。由于有限元分步算法具有计算效率高，精度得到保证，编程较为简单等优点[15]，文中采用该方法对三维方腔流问题进行数值模拟。

计算能力不足是计算流体力学发展所面临的一大挑战。为解决大规模计算问题，并行化是大幅度提高计算效率的最有效手段。常用的并行化方法有线性代数方程组的并行计算和区域分解法两种。并行计算工具箱PETSc(Portable, Extensible Toolkit for Scientific Computation)提供了并行计算线性代数方程组的库函数。软件包 PETScFEM 基于并行计算工具箱 PETSc，将非重叠区域分解法应用于计算流体力学的有限元分析中，实现了不可压粘性流体力学问题的并行计算。

本文基于PETScFEM开源代码[16-17]，采用分步有限元算法对不可压粘性流体进行求解，并结合区域分解法并行计算了不同雷诺数下的顶板斜向驱动方腔流问题。数值模拟时首先对计算区域进行有限元离散，不可压 Navier-Stokes 方程中的速度和压力采用同阶的线性形函数和权函数，时间离散采用后退欧拉法；采用基于 Poisson 投影的分步算法对速度和压力进行解耦，并形成三个子方程；计算网格通过非重叠的区域分解法进行剖分，并分配到不同的CPU中并行计算，MPI(Message Passing Interface)库函数用于各子区域间并行计算数据通信，离散后的线性代数方程组采用 GMRES(Generalized Minimal RESidual)结合 Jacobi 预处理方法进行计算。在之前的工作中[18]，已采用该方法对顶板正向驱动方腔流问题进行了数值模拟，计算结果表明该方法计算效率高，精度较好。在此基础上，文中的主要工作是对雷诺数为100、400、1 000和2 000的顶板斜向驱动方腔流进行并行数值模拟。

本文结构安排如下：首先描述不可压粘性流体控制方程及分步有限元算法，其次介绍非重叠区域分解并行算法，然后对不同雷诺数下的顶板斜向驱动方腔流进行数值模拟，给出速度矢量图、压力等值面、流线、涡量等值线以及中心垂线上的速度剖面等流场结构信息，并进行并行性能分析，最后给出结论。

1 数值算法

1.1 问题描述及控制方程

图1 三维顶板斜向驱动方腔流计算模型Fig. 1 Computational model of 3D lid-driven cubic cavity flow at yaw

粘性流体流动可用 Navier-Stokes 方程进行求解。对于不可压缩流体流动，其控制方程包含动量守恒方程和质量守恒方程：

∂tu+u·u+

1.2 时间和空间离散

为了方便描述有限元空间离散式，引入如下记号：

a(u,v):=ν(u,v),b(q,v):=(q,v),c(u,v,w):=(u·v,w)

(∂tu,v)+c(u,u,v)+a(u,v)-b(p,v)=0 ∀v∈V,

b(q,u)=0 ∀q∈Q

采用梯形法则对方程进行整体时间离散，即同时求解速度和压力。简单起见，将时间 [0,T] 划分为N个均匀的时间步，时间步长为δt。令f为关于时间的通用函数，fn为函数f在tn=nδt时刻的值，fn+θ:=θfn+1+(1-θ)fn，δtfn:=(fn+1-fn)/δt，其中θ∈[0,1]，则弱解方程的时间离散式为：

当θ=1/2时，该方程对应于二阶的 Crank-Nicolson 时间离散，当θ=1时，该方程对应于向后 Euler 时间离散。

令Vh为V的近似有限元空间，Qh为Q的近似有限元空间，Vh空间中的函数要求为分段连续多项式，Qh空间中函数的连续性不要求，则方程(3)～(4)的有限元空间离散式为：

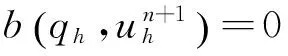
在基于压力 Poisson 方程的分步算法中，当时间步长较大时，速度和压力插值函数不需要满足 LBB 条件，因此在本文的计算中速度和压力插值函数均采用一阶线性多项式。

方程(5)～(6)的矩阵形式可表示为：

式中：U和P分别表示结点速度和压力数组，M为质量矩阵，K为包含扩散项和对流项的矩阵，G为梯度矩阵，D为散度矩阵。

1.3 分步算法

方程(7)～(8)等价于如下的方程组：

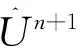
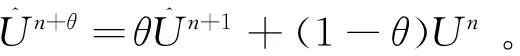
1.4 区域分解法

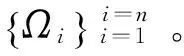
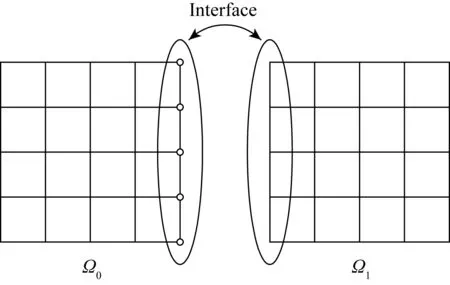
图2 非重叠区域分解法计算模型(2个子区域)Fig. 2 Computational model of non-overlapping domain decomposition

令Aii,i=1,2,…,n为各子区域Ωi内部结点所形成的矩阵，ALL=diag[A11,A22,…,Ann]为分块对角矩阵，AII为各子区域间交界面结点所形成的矩阵。相应地，令x=(xL,xI)T，y=(yL,yI)T，则代数方程组可分裂为：

式中：ALI和AIL为子区域内部结点和交界面结点的连接关系矩阵。该方程组的求解可以分为两步完成，首先求解方程(17)获得交界面结点的变量值xI，各子区域间的数据通信通过 MPI 库函数来完成，然后再并行求解方程(18)，得到各子区域内部结点的变量值xL：

2 数值模拟结果

首先模拟雷诺数为1 000时的顶板斜向驱动方腔流，进行了网格收敛性验证，并给出速度矢量图、压力等值面、流线、涡量等值线等流场信息。其次模拟雷诺数为100，400，2 000等不同顶板斜向驱动方腔流，比较不同雷诺数对顶板斜向驱动方腔流的影响。

2.1 雷诺数为1 000时的顶板斜向驱动方腔流

首先模拟雷诺数为1 000时的顶板斜向驱动方腔流。计算采用三套不同精度的均匀六面体网格进行网格收敛性验证，粗、中、细网格的单元数分别为 36×36×36、48×48×48、64×64×64。计算时间步长取为 0.05，迭代1 000步均能得到收敛的结果。计算结果表明，中等精度网格已能得到较好的结果，而计算时间却比细网格少很多。图3所示结果为中等精度网格计算结果。

雷诺数为1 000时顶板斜向驱动方腔流的流线分布如图3 所示。从正视图可以看出，流体由顶板驱动，以45°角撞击x=1的下游侧壁和y=1的下游侧壁，撞击后的流体在由两侧壁构成的角落处汇聚，并形成一股强大的射流射向底面。从后视图可以看出，射流撞向底面后在底面呈90°扇形散开。流体在遇到x=0的上游侧壁和y=0的上游侧壁后转而向上流动，最终汇入顶板附近流体，完成一次循环。从侧视图可以看出，由于顶板驱动流体的汇聚和射流的形成，使得主涡变得倾斜而狭长，且有流体从下游侧壁中心附近汇入主涡中。

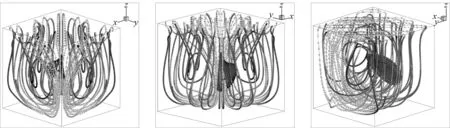
图3 雷诺数为1 000时流线分布的不同视角(左：正视图，中：后视图，右：侧视图)Fig. 3 Streamlines at Re=1 000: front view (left); back view (middle); oblique view (right)

从图5可看到方腔流不同剖面的速度矢量投影。在CP剖面中，由于流体的堆积和射流的形成，可以看到主涡在平面的左下方，而右下角可看到次级涡的存在。在CP2剖面中，涡心位于剖面中央，平均速度较CP平面小。在CP3剖面中，涡心位于平面右上角，且大部分区域的速度矢量向上。从PP剖面和MP剖面的速度矢量投影中，可以看到二次涡的存在。本文结果与Povitsky的计算结果[9]基本一致。

图6 所示为雷诺数为1 000时顶板斜向驱动方腔流速度大小等值面。从图6(a)中可以看到，由顶板带动的流体在由x=1的下游侧壁和y=1的下游侧壁形成的垂直角落里汇聚形成一股速度较大的射流。图6(b)则显示了由顶板带动的流体在撞击下游侧壁后汇聚的过程。图6(c)显示了射流在撞击底面之后朝两个方向散开的低速射流。图6(d)、6(e)和6(f)分别显示了顶板驱动流体在到达底面之后呈扇形面散开，在遇到x=0的上游侧壁和y=0的上游侧壁后转而向上流动，由于流体运动空间的增大和壁面粘性的阻滞作用，这一过程中流体的速度逐渐降低。

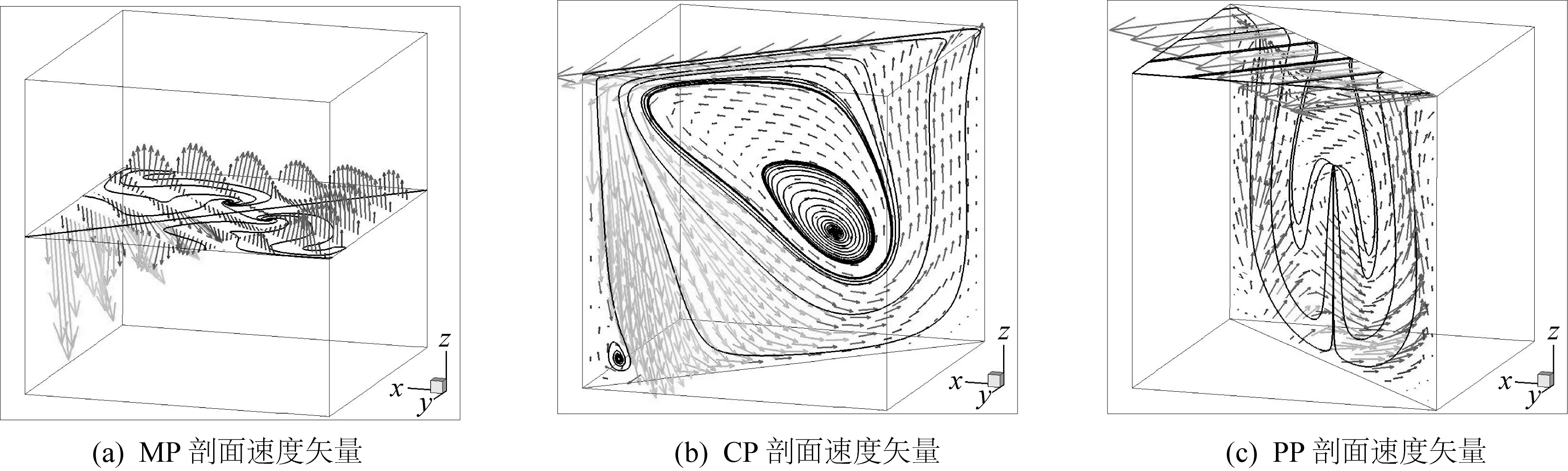
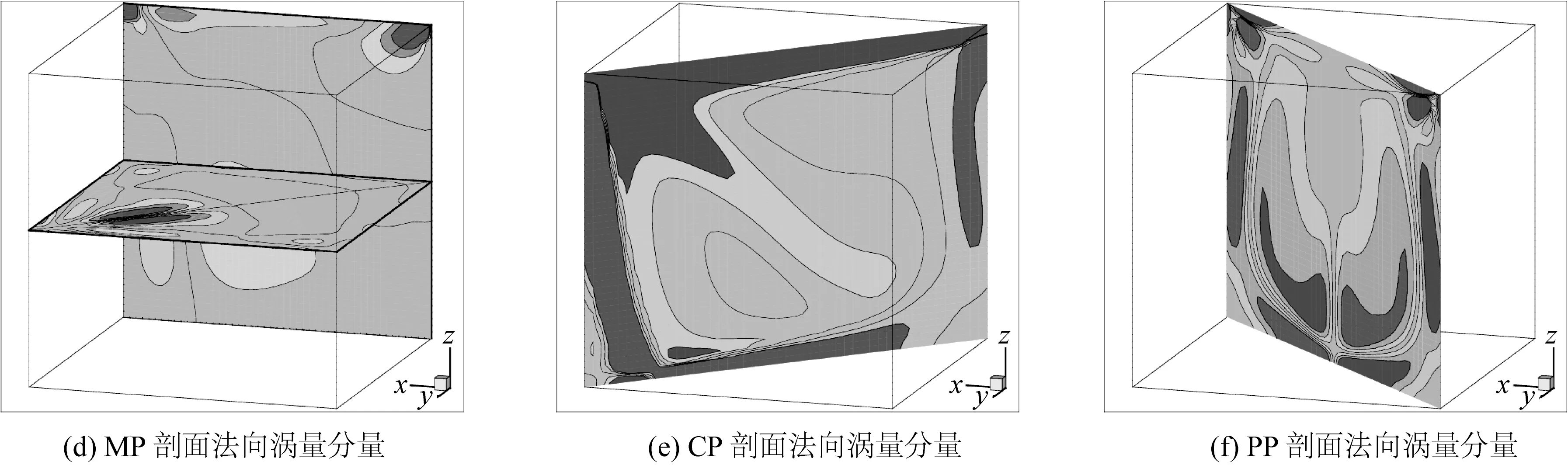
图4 不同剖面的速度矢量和流线投影及其法向涡量分量(Re=1 000)Fig. 4 Perspective 3D solution summary at Re=1 000

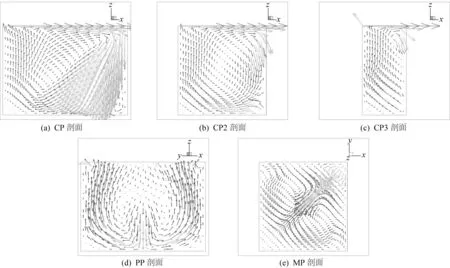
图5 不同剖面的速度矢量投影分布(Re=1 000)Fig. 5 2D planar projections of velocity vector at Re=1 000 on different planes

图7 所示为雷诺数为1 000时顶板斜向驱动方腔流的压力等值面。图8所示为雷诺数为1 000时不同精度网格计算结果(沿 CP 剖面中垂线的水平速度分量)比较。从图8中可以看到，从粗网格到细网格，计算结果逐渐收敛，中等精度网格与细网格计算结果基本保持一致。由于中等精度网格已能得到较好的计算精度，而网格单元数却比细网格少很多，可以减少大量的计算时间，因此在本文其它的工况计算中均采用中等精度网格进行计算。从速度剖面看，水平速度分量在底面附近存在一个峰值，该峰值由底面射流产生。在距底面0.1～0.3的区域速度绝对值均较大，由流体的汇聚挤压引起。

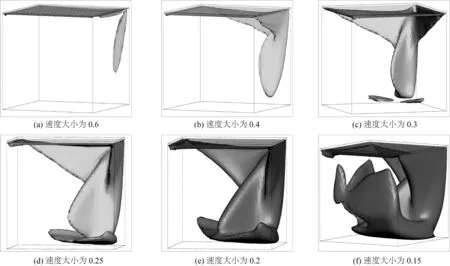
图6 顶板斜向驱动方腔流速度大小等值面(Re=1 000)Fig. 6 Iso-surfaces for different velocity magnitudes at Re=1 000

图7 压力等值面(Re=1 000)Fig. 7 Pressure iso-surfaces at Re=1 000

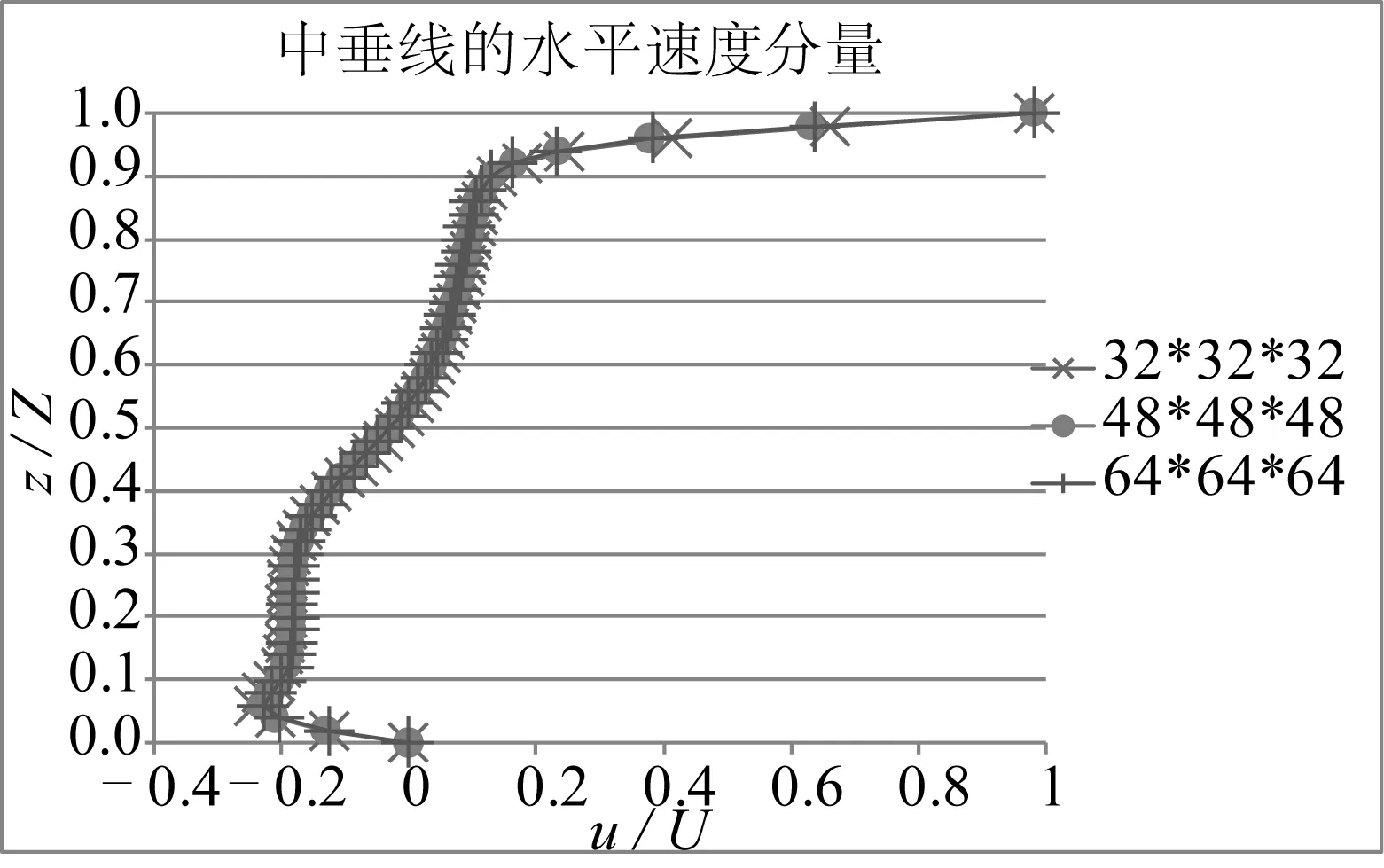
图8 沿CP 剖面中垂线的水平速度分量(Re=1 000)Fig. 8 Horizontal component velocity profile at Re=1 000

2.2 不同雷诺数对顶板斜向驱动方腔流的影响

本文还模拟了雷诺数为100、400和2 000时的顶板斜向驱动方腔流，并考察不同雷诺数对顶板斜向驱动方腔流的影响。本节计算采用48×48×48的均匀六面体网格，单元特征尺度为0.020 83。计算时间步长取为0.05，迭代1 000步均能得到收敛的结果。

图9所示为雷诺数为100、400和2 000时顶板斜向驱动方腔流的流线分布。从图中可以看出，随着雷诺数的增加，流线由简单变为复杂，特别是主涡流线，当雷诺数为2 000时变得杂乱。

图10所示为不同雷诺数下CP剖面内速度矢量投影。从图中可以看出，随着雷诺数的增加，主涡涡心位置不断变化，当雷诺数为100时，主涡位于中部偏上的位置，当雷诺数为400时，主涡中心在右上角，当雷诺数为1 000时，主涡变为倾斜狭长的卵形，涡心在平面的左下方，当雷诺数达到2 000时，涡心位置更靠近底面。此外，当雷诺数为400时，可以看到较为明显的下游二次涡。当雷诺数达到2 000时，可以明显地观察到上游二次涡的形成。

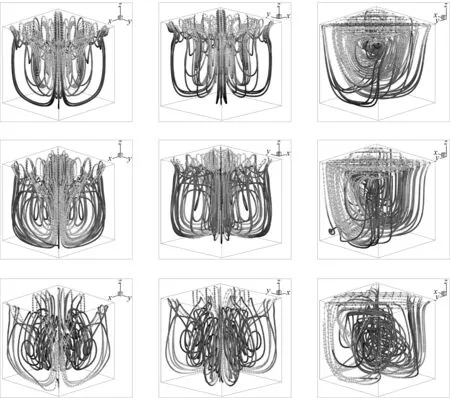
图9 不同雷诺数(从上至下：Re=100，400，2 000)流线分布的不同视角(从左至右：正视图，后视图，侧视图)Fig. 9 Streamlines for different Reynolds numbers

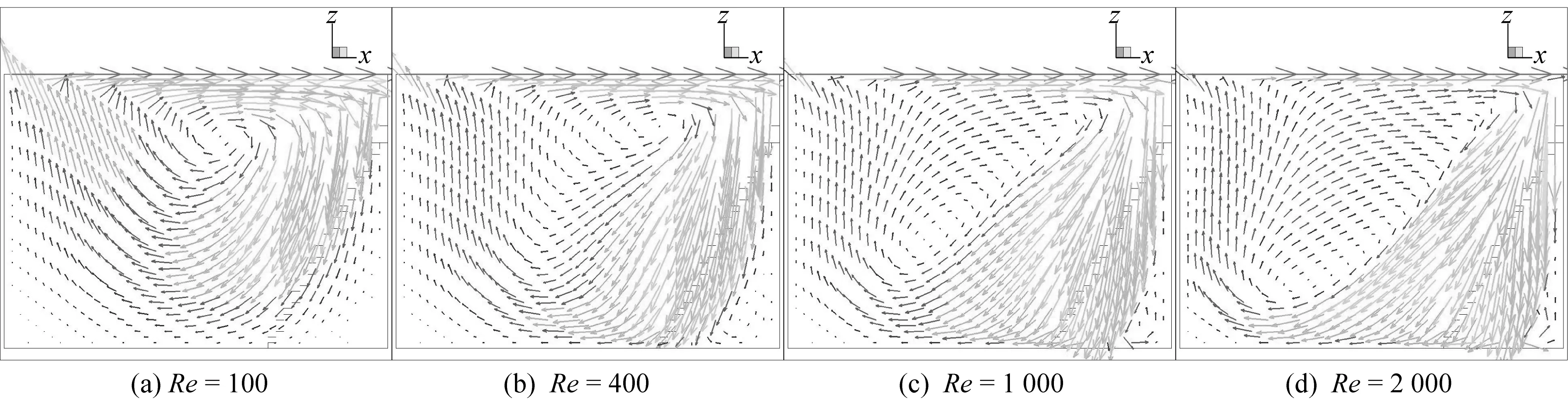
图10 不同雷诺数下CP剖面内速度矢量投影Fig. 10 2D planar projections of velocity vector on CP plane for different Reynolds numbers

图11所示为不同雷诺数下 MP 剖面内速度矢量投影(本文结果)。从图中可以看出，随着雷诺数的增加，二次流变得越来越复杂，当雷诺数为1 000时，可以观察到3对二次涡，而当雷诺数增加到2 000时，可以观察到6对二次涡。图12所示为Povitsky的计算结果[9]。将本文结果与参考结果进行比较，可以看出对应的漩涡个数及漩涡形态均保持一致。

图11 不同雷诺数下MP剖面内速度矢量投影(本文结果)Fig. 11 2D planar projections of velocity vector on MP plane for different Reynolds numbers (our results)

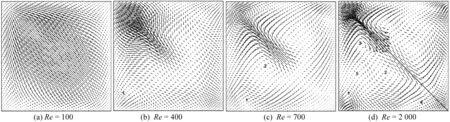
图12 不同雷诺数下MP剖面内速度矢量投影(参考结果)Fig. 12 2D planar projections of velocity vector on MP plane for different Reynolds numbers (reference results)

图13所示为不同雷诺数下沿CP剖面中垂线的水平速度分量。从图中可以看到，随着雷诺数的增加，边界层的厚度逐渐减小。当雷诺数为100时，粘性作用较强，壁面的阻滞效应较大，速度剖面变化较为平缓。当雷诺数为400时，底面附近已形成射流，因此出现了较大的峰值。当雷诺数为1 000时，底面附近的射流峰值有所减小，但流体的堆积挤压现象较为明显，导致距底面0.1～0.3附近的速度绝对值较大。当雷诺数达到2 000时，流体堆积挤压现象更为严重，使得流体在距底面0.2附近出现峰值。

图13 不同雷诺数下沿CP剖面中垂线的水平速度分量Fig. 13 Horizontal velocity component along the vertical midline of the CP plane at different Reynolds numbers

不同雷诺数下沿 CP 剖面中垂线的水平速度分量数值如表1所示。

2.3 并行性能

本文采用网格非重叠区域分解法结合消息传递的模式进行并行计算，非重叠网格区域划分的方式如图14所示。以雷诺数为1 000的顶板斜向驱动方腔流计算为例，取时间步长为0.05，迭代1 000步，不同进程数(从1到8)的计算时间及加速比如表2所示，相对应的曲线如图15所示。从图中可以看出，随着进程数的增加，计算时间不断减少，并行加速比不断增大，但由于进程间数据传递量的增加，加速比的增长速度比线性增长速度为小。

表1 不同雷诺数下沿 CP 剖面中垂线的水平速度分量Tab. 1 Horizontal velocity component along the vertical midline of the CP plane at different Reynolds numbers

图14 不同块数的区域分解网格Fig. 14 Domain decomposition meshes for different domains

进程数12345678时间/s4323020520156601286010540951791288171加速比12.10672.76053.36164.10154.54244.73605.2907

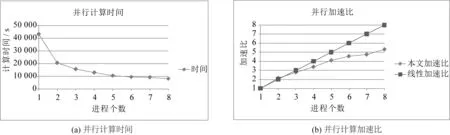
图15 并行性能分析Fig. 15 Analysis of the parallel performance

3 结 语

采用分步有限元算法结合非重叠区域分解法并行计算了不同雷诺数(100、400、1 000 和2 000)下的顶板斜向(斜向角为 45°)驱动方腔流问题。从计算结果可以看出，顶板斜向驱动方腔流具有较为复杂的涡流结构。由顶板驱动的流体以45°角撞击x=1的下游侧壁和y=1的下游侧壁后汇聚成一股速度较大的射流，该射流在底面呈扇形散射，在遇到x=0的上游侧壁和y=0的上游侧壁后转向上流动，最终汇入顶板附近流体并进入循环。在这一循环过程中，由于主流运动方向与侧壁呈45°偏角，使得二次流现象较为明显和复杂。且随着雷诺数的增加，流动更为剧烈，整个涡流场结构也更为复杂。

计算表明，采用基于Poisson投影的分步算法后，应用传统的有限元方法即能很好地求解不可压粘性方腔流问题。同时，结合网格区域分解和消息传递的并行计算模式，可以得到很好的并行计算性能。开源软件PETScFEM为计算不可压粘性流体问题提供了很好的工具，且为进一步开发提供了很好的平台。

[1] AIDUN C K, TRIANTAFILLOPOULOS N G, BENSON J D. Global stability of a lid-driven cavity with through flow: flow visualization studies [J]. Physics of Fluids, 1991, 3: 2081-2091.

[2] PRASSAD A K, KOSEFF J R. Reynolds number and end-wall effects on a lid-driven cavity flow [J]. Physics of Fluids, 1989,1(2): 208.

[3] JIANG B N, LIN T L, POVINELLI L A. Large scale computation of incompressible viscous flows by least-squares finite element method [J]. Computer Methods in Applied Mechanics and Engineering, 1994, 114(3-4): 213-231.

[4] WONG K L, BAKER A J. A 3D incompressible Navier-Stokes velocity-vorticity weak form finite element algorithm [J]. International Journal for Numerical Methods in Fluids, 2002, 38(9): 9-23.

[5] LERICHE E. Direct numerical simulation in a lid-driven cubical cavity at high reynolds number by a chebyshev spectral method [J]. Journal of Scientific Computing, 2006: 335-345.

[6] HACHEM E, RIVAUX B, KLOCZKO T, et al. Stabilized finite element method for incompressible flows with high Reynolds number [J]. Journal of Computational Physics, 2010, 229: 643-665.

[7] ZANG Y, STREET RL, KOSEFF JR. A dynamic mixed subgrid-scale model and its application to turbulent recirculating flows [J]. Physics of Fluids, 1993, 5: 3186.

[8] SHANKAR PN, DESHPANDE MD. Fluid mechanics in the driven cavity [J]. Annual Review of Fluid Mechanics, 2000, 32: 93-136.

[9] POVITSKY A. Three-dimensional flow in cavity at yaw [J]. Nonlinear Analysis, 2005, 63(5-7): 1573-1584.

[10] 任安禄. 不可压缩粘性流场计算方法 [M]. 北京: 国防工业出版社, 2003.(REN Anlu. Numerical methods in incompressible viscous flow [M]. Beijing: National Defence Industry Press, 2003.(in Chinese))

[11] 章本照，印建安，张宏基. 流体力学数值方法 [M]. 北京: 机械工业出版社, 2003. (ZHANG Benzhao, YIN Jianan, ZHANG Hongji. Numerical methods in fluid dynamics [M]. Beijing: China Machine Press, 2003.(in Chinese))

[12] 王献孚，周树信，陈泽梁，等. 计算船舶流体力学 [M]. 上海: 上海交通大学出版社, 1991. (WANG Xianfu, ZHOU Shuxin, CHEN Zeliang, et al. Computational ship hydrodynamics [M]. Shanghai: Shanghai Jiao Tong University Press, 1991.(in Chinese))

[13] GUERMOND J L, QUARTAPELLE L. On stability and convergence of projection methods based on pressure poisson equation [J]. International Journal for Numerical Methods in Fluids, 1998, 26: 1039-1053.

[14] CONDINA R. Pressure stability in fractional step finite element methods for incompressible flows [J]. Journal of Computational Physics, 2001, 170(1): 12-40.

[15] 刘淼儿，任玉新，张涵信. 数值求解不可压缩流动的投影方法研究进展 [J]. 力学进展, 2006, 36(4): 591-598. (LIU Miaoer, REN Yuxin, ZHANG Hanxin. Review on the projection methods in the numerical solution of the incompressible flow [J]. Advances in Mechanics, 2006, 36(4): 591-598.(in Chinese))

[16] PAZ R R, NIGRO N M, STORTI M A. On the efficiency and quality of numerical solutions in CFD problems using the interface strip preconditioner for domain decomposition methods [J]. International Journal for Numerical Methods in Fluids, 2006, 52(1): 89-118.

[17] SONZOGNI V E, YOMMI A M, NIGRO N M, et al. A parallel finite element program on a Beowulf cluster [J]. Advances In Engineering Software, 2002, 33(7-10): 427-443.

[18] WANG J F, WAN D C. Parallel simulation of 3D lid-driven cubic cavity flows by finite element method [C]// Proceedings of the 21st International Offshore and Polar Engineering Conference. Hawaii:[s.n.], 2011: 644-651.

Parallel simulation of 3D lid-driven cubic cavity flows at yaw by finite element method

WANG Jifei1,2, WAN Decheng1,2

(1. State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China; 2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China)

The fractional step finite element method and domain decomposition method are applied to simulate in parallel the 3D lid-driven cubic cavity flows at yaw based on the open source codes PETScFEM. When the lid moves along its diagonal, the driven fluid impinges in the spatial angle formed by the downstream side walls, which leads to formation of the jet flow. A system of vortices is caused when the jet flow impinges the bottom wall and upstream side walls. Different Reynolds numbers are investigated, which show the significant influence for this flow. Parallel performance analysis reveals that the domain decomposition method can efficiently speed up the simulation of 3D lid-driven cavity flows.

3D cavity flow, yaw angle, finite element method, domain decomposition, parallel simulation

O351

A

10.16483/j.issn.1005-9865.2015.02.001

1005-9865(2015)02-0001-12

2014-01-06

国家自然科学基金资助项目(51379125，11432009,51490675)；上海高校特聘教授(东方学者)岗位跟踪计划项目(2013022)；国家重点基础研究发展计划(973计划)项目(2013CB036103)；工信部高技术船舶科研项目；上海交通大学高性能计算中心(HPC)资助项目

王吉飞(1984-)，男，重庆人，博士研究生，从事计算流体力学研究。E-mail：wangjifei2000@126.com

万德成。E-mail：dcwan@sjtu.edu.cn