强台风下导管架平台倒塌全过程数值仿真

朱本瑞，陈国明，林 红，刘红兵，黄 超

(中国石油大学 海洋油气装备与安全技术研究中心，山东 青岛 266580)

强台风下导管架平台倒塌全过程数值仿真

朱本瑞，陈国明，林 红，刘红兵，黄 超

(中国石油大学 海洋油气装备与安全技术研究中心，山东 青岛 266580)

针对强台风引起的平台倒塌问题，综合隐式有限元与显式动力有限元算法，建立导管架平台结构倒塌全过程仿真流程；提出基于重现期的Pushover分析方法，充分考虑平台侧向环境载荷分布的变化以及可能的甲板上浪载荷因素，使得确定的倒塌环境载荷更加真实；采用APDL编制平台隐式与显式有限元模型转化程序，有效解决波浪载荷计算与精确施加的难题；在此基础上，应用LS-DYNA实现导管架平台在强台风载荷下的倒塌全过程仿真，动态再现平台结构倒塌过程中的构件破坏失效及内力分布，深入揭示平台结构的倒塌机理。研究成果可为导管架平台结构抗台风设计及理论研究提供参考。

台风；导管架平台；甲板上浪；极限状态；倒塌机理；LS-DYNA；数值仿真

台风引起的极端风载和巨浪载荷是导致海洋平台结构破坏的两大重要因素，两者联合作用极有可能造成导管架平台整体倾覆或倒塌。2002至2004年，台风Lili与Ivan分别造成7座导管架平台倒塌[1]；2005年Katrina和Rita相继摧毁115座固定平台[2]。这一系列的事故引起了国内外学者对台风灾害的重视，文献[3-7]分别从台风风载模拟、连续性倒塌动力响应、极限承载能力、失效模式分析以及可靠性等角度对极端载荷下导管架平台结构的抗倒塌性能进行了研究，然而这些研究通常只针对结构极限状态前的情形，而没有对包括倒塌在内的全过程进行分析，显然，这对于预防结构倒塌还远远不够。

倒塌是一个非常复杂的非线性动力过程，涉及到不连续位移场的描述，接触与碰撞以及倒塌过程中的大位移、大转动问题，目前主要通过数值模拟技术进行研究。常用的方法包括：修正有限元方法，离散单元法，在已有有限元软件如ANSYS、MARC等基础上进行二次开发，显式动力有限元法[8]。其中，显式动力有限元已被广泛使用，文献[9]和[10]分别利用LS-DYNA对多层平面钢框架和纽约世贸中心进行了连续倒塌仿真。但是，这些仿真均集中于框架或混凝土等建筑结构，而对于钢制导管架平台的倒塌模拟尚未见诸报道。显然，海洋平台结构在受到的载荷类型、载荷分布、几何拓扑结构以及内力传递机制上与建筑类结构迥然不同，因此，如何借鉴已有研究成果开展导管架平台倒塌全过程的数值模拟，揭示其倒塌机制成为学术界研究的难点。笔者综合运用隐式有限元和显式动力有限元的优点，建立一套导管架海洋平台结构倒塌全过程的数值仿真流程，并以某深水导管架平台为例，再现平台在台风引起的极端环境载荷作用下的倒塌全过程，从而实现平台结构的载荷传递路径以及内力重分布的可视化，为进行平台结构弱点分析、倒塌预防与控制提供重要参考。

1 导管架平台倒塌全过程仿真技术流程

1.1 平台倒塌仿真流程

与建筑类结构倒塌仿真相比，海洋平台倒塌模拟过程更为复杂，不仅需要考虑结构自重，还应考虑恶劣的海洋环境载荷。为此，采用ANSYS软件，结合隐式算法与显式算法的优点，构建平台结构倒塌仿真的流程，如图1所示。

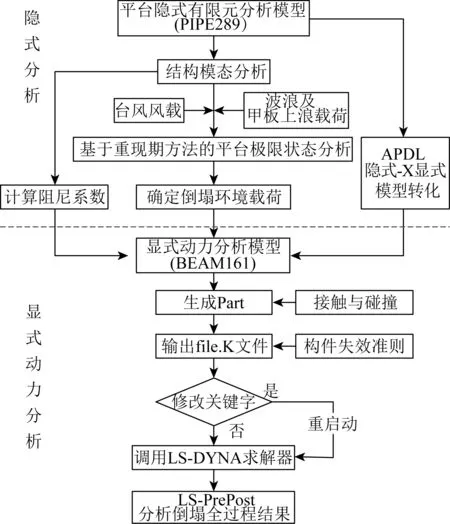
图1 导管架平台结构倒塌全过程仿真流程Fig. 1 Simulation flowchart for entire collapse process of jacket platform

由图1可知，隐式分析包括模态分析和结构极限承载能力分析，分别用于确定结构显式动力分析时的阻尼系数和倒塌环境载荷，此外，隐式程序提供的波浪载荷模拟模块OCEAN，可以方便有效地计算波浪载荷，大大简化了环境载荷计算问题；显式动力分析则是通过LS-DYNA技术，用于处理平台倒塌过程的大变形、大转动等多维非线性问题，并可以充分考虑倒塌过程中的构件断裂、接触与碰撞，从而实现平台结构在越过极限状态后的力学行为仿真。

1.2 显式有限元中波浪载荷的施加

倒塌仿真的准确性关键在于波浪载荷的精确施加。ANSYS中能够计算波浪的单元包括PIPE59、PIPE288和PIPE289，这些单元仅能够在隐式求解器中使用，而显式有限元LS-DYNA尚不具备波浪载荷的计算功能。为此，采用APDL编制隐式与显式有限元模型等效转化程序，从隐式有限元波浪载荷计算模块中提取平台构件上的波浪载荷，再施加于显式有限元中构件中，从而达到倒塌波浪载荷等效施加的目的。采用这种方式时，应满足隐式有限元模型与显式模型任意构件的I节点与J节点的空间坐标一致，且单元坐标方向一致(可通过方向节点控制)。

2 导管架平台极限状态与倒塌环境载荷

平台结构倒塌过程与侧向载荷分布密切相关，因此，准确模拟平台结构倒塌全过程，首先需要确定平台达到极限状态时对应的环境载荷。平台结构极限状态可采用静力推覆分析(Pushover)方法确定[11]，该方法是对平台施加100年一遇的环境载荷，并将其逐级进行放大，直至结构发生倒塌，从而对平台倒塌机制和抗力水平进行评估。然而，这种加载方式忽略了平台结构侧向载荷分布的变化，确定的倒塌状态与环境载荷大小不够真实。事实上，造成平台倒塌的环境载荷较大，其概率往往远小于1/100，特别地，当平台倒塌时的波峰高度大于甲板设计高程时，平台将发生甲板上浪载荷现象，从而极大地改变结构的侧向载荷分布与倒塌模式[12]，为此，笔者提出基于不同重现期的环境载荷，采用渐进加载方式，进行平台极限状态分析，充分考虑不同风、浪、流对环境载荷分布的影响，以及可能的甲板上浪因素，从而确定平台结构真实的倒塌状态与对应的环境载荷。

采用重现期为变量进行极限状态分析时，需要额外考虑两方面的计算：一是计算不同重现期对应的环境参数，以确定加载序列的环境载荷值；二是当波高大于平台甲板高程时，应考虑甲板上浪载荷引起的抨击载荷，即需要确定上浪载荷计算方法。

2.1 环境参数极值推算

台风或强台风引起的极端环境载荷是一种发生频率相对较高的极值载荷，可采用三参数Weibull极值分布对极端环境载荷要素进行推算[13]，于是有：

由此，计算得到环境载荷参数极值xp为：

式中：参数α、μ和ξ分别为尺度参数、位置参数和形状参数，可根据极大似然估计法计算得到。

2.2 甲板上浪载荷

甲板上浪形成的冲击载荷对平台上部结构、设备等造成巨大破坏，严重的甲板上浪甚至导致平台倾覆，MMS研究报告表明，在台风摧毁的平台中，由甲板上浪载荷造成的占21%。然而，迄今为止甲板上浪载荷的计算尚没有普遍认可的方法。现有的方法大致可分为侧面轮廓法和细节构件法两大类。其中侧面轮廓法又包括API模型、DNV拍击力模型、SHELL模型和MSL模型等，各种模型的详细讨论可参考文献[14-15]。本文选用API模型来计算甲板上浪载荷，其公式为[11]：

式中:ρ为海水密度(kg/m3)；Cd为拖曳力系数；vx为甲板淹湿顶部处水质点水平速度(m/s)；vuc为与波浪同向的流速(m/s)；awkf为波浪运动系数，台风时取0.88；acbf为导管架的海流阻挡系数；A=zwd×b，为甲板淹湿轮廓在波浪方向的投影面积(m2)，zwd为波浪淹没甲板的高度(m)，b为甲板宽度(m)。

计算甲板上浪关键在于确定甲板淹湿位置处的波面高度及水质点水平速度，可根据Stokes 5th波理论建立的色散关系方程组采用牛顿法编程求解波长L和系数λ，然后代入波面公式和速度公式计算得到[16]。

3 LS-DYNA动力倒塌仿真方法

3.1 LS-DYNA分析原理

进行强台风作用下平台结构倒塌显式动力分析时，其离散化动力方程可表示为：

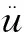
式中:[M]、[C]和[K]分别为平台结构系统的质量矩阵、阻尼矩阵和刚度矩阵；{u}t分别为加速度矩阵、速度矩阵和刚度矩阵；{F}t为台风引起的环境载荷向量。将式(4)中的速度与加速度用离散的位移表示，并用中心差分代替微分，则有{t=({u}t+Δt-{u}t-Δt)/2Δt、{t=({u}t-Δt-2{u}t+{u}t+Δt)/Δt2，带入式(4)，并整理得：

由上述推导过程可知，采用中心差分方法只需代入初始条件，即可求得t+Δt瞬时的位移向量{u}t+Δt，再将{u}t+Δt代入几何方程与物理方程中从而获得t+Δt时刻的单元应力和应变。由于LD-DYNA方程为非耦合，且无须进行非线性刚度矩阵的逆运算，因而可以有效地避免程序在求解大变形、大转动时的不收敛问题，从而实现平台倒塌动态过程的模拟。

3.2 倒塌仿真关键技术

为使倒塌过程模拟的结果更加真实可靠，除保证波浪载荷施加精确外，还应考虑结构阻尼、接触-碰撞以及失效准则。其中结构阻尼系数可采用经验公式由平台结构模态分析获得的前两阶固有频率计算得到[4]，阻尼系数的定义可以消除分析过程构件不真实的振荡。

由于结构大变形以及断裂构件的脱落、冲击作用，平台倒塌过程中不可避免地造成构件间的接触与碰撞。因此，必须解决倒塌过程中的接触与碰撞问题，以防止构件间发生不真实的穿透。LS-DYNA提供了罚函数法、动态约束法和分布参数法3种接触算法，以及不同种类的接触类型。其中罚函数法编程简单，且动量守恒准确，引起的Hourglass效应小，是LS-DYNA最常用的算法[17]。故此本文选用罚函数方法，并设置接触类型为自动单面AG，使得程序能够搜索所有构件间的接触，以充分模拟平台倒塌过程中不可预测的接触与碰撞情况。

合理的破坏准则是进行倒塌仿真的前提。LS-DYNA包括两种定义失效准则的方式，一是通过添加关键字*MAT_ADD_EROSION使构件达到某一条件时发生失效；二是采用带有失效准则的材料本构。由于前者仅适用于单点积分的2D或3D体单元，因此，采用第二种方式，材料本构关系选用随动塑性模型，定义失效应变为0.2，其余参数见表1。

表1 随动塑性材料模型参数Tab. 1 Parameters of plastic kinematic model

4 倒塌仿真实例

4.1 有限元模型及环境载荷

某海洋平台设计水深107 m，导管架由7层构成，4根桩管成双斜对称结构，其中ROWA和ROWB面斜撑为K型布置，ROW1和ROWB2面在66 m以下采用K型斜撑，66 m以上采用对角斜撑；平台上部组块宽25 m，长45 m，重6 033 t(包括设备重量)，底层甲板高程为15 m。建立平台结构隐式和显式有限元模型分别如图2(a)和2(b)所示。其中隐式模型中导管架采用PIPE289单元建立，上部组块结构进行简化，设置为线弹性单元，设备质量采用MASS21单元模拟；模型中忽略桩-土非线性相互作用，导管架底部简化为固支约束。显式有限元模型采用APDL由隐式模型转化生成，其中导管架结构为BEAM161单元，质量单元为MASS166；此外，模型中增加了海底单元，以模拟平台倒塌时与海底的接触，海底采用SHELL163单元建立，并设置为刚体。

图2 海洋平台有限元模型Fig. 2 Finite element model of the platform

根据中国科学院南海海洋研究所对1948～2008年间的环境载荷统计资料进行分析，得到不同环境要素的Weibull分布参数估计值，见表2。

由表2中估计参数，计算得到该海域不同重现期对应的风速、波高、周期及流速的极值以及甲板上浪，见表3，其中上浪载荷由公式(3)计算得到，系数Cd取2.5，acbf取0.8，b为45 m。

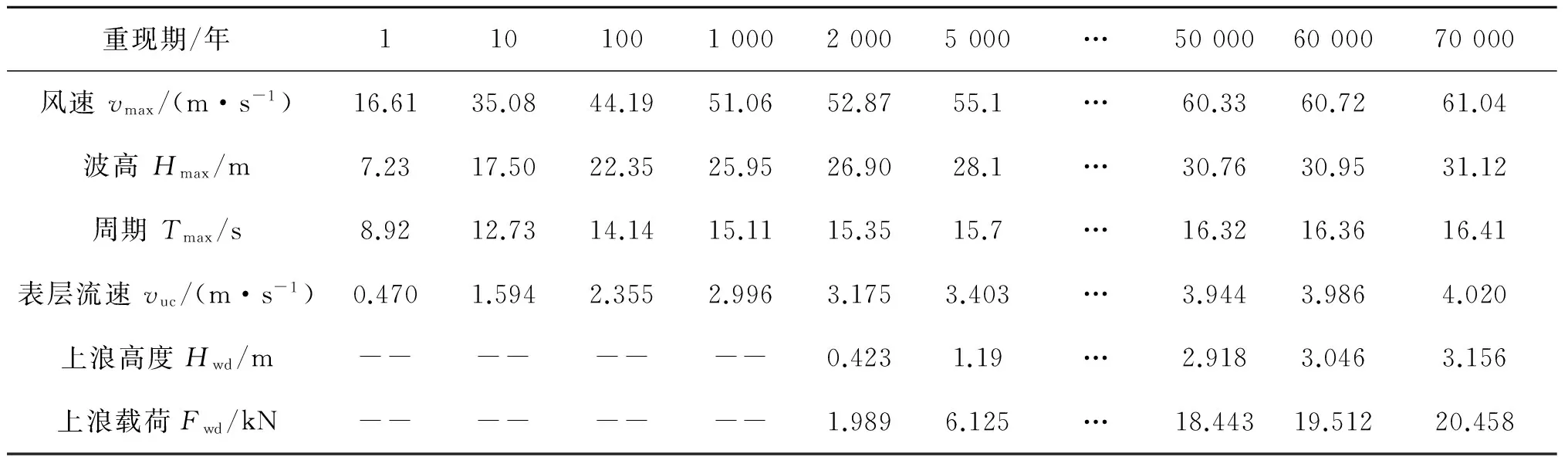
表3 环境载荷参数及上浪载荷部分数据表Tab. 3 Partial environmental load parameters and WID loads

由表3可知，平台100年一遇设计环境参数为：波高22.4 m，周期14.1 s、表层流速2.355 m/s，最大风速44.2 m/s，由此计算得平台正面(0°)最大波流载荷为15 903.9 kN(对应最大相位角为32°)，风载为1 298.4 kN。此外，应注意到当载荷重现期为2 000年时，平台开始出现甲板上浪，重现期为50 000年时，上浪高度为2.92 m，上浪载荷达到18 443 kN，略大于设计环境载荷，可见上浪载荷对平台侧向载荷的分布影响较大。

4.2 平台极限状态分析

采用基于重现期的Pushover对该平台进行极限状态分析，得到平台结构的等效承载能力曲线，如图3所示。由图3可知，平台结构在弹性响应阶段，当发生上浪载荷时，等效承载能力曲线出现拐点，平台上浪载荷对平台载荷分布及结构响应影响较大；当重现期为50 000年时，平台结构进入塑性响应阶段；当重现期为70 000年，计算结果不收敛，平台达到极限状态，最大极限承载能力为58 423.7 kN，储备强度比RSR=3.4。由表3中数据可知，此时对应的倒塌环境载荷参数为：风速61 m/s，波高31.1 m。

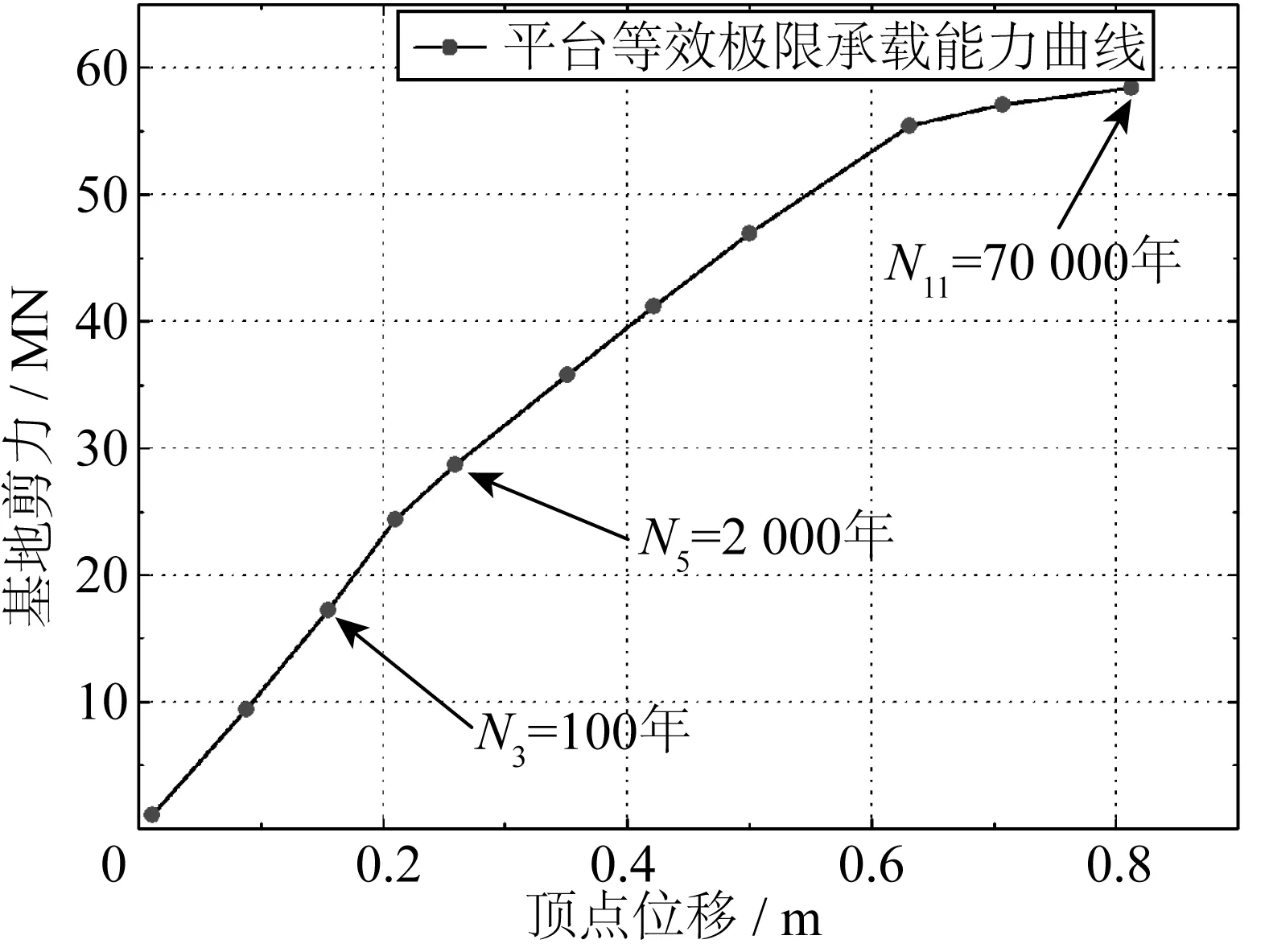
图3 平台等效承载能力曲线Fig. 3 Equivalent bearing capacity curve of platforms

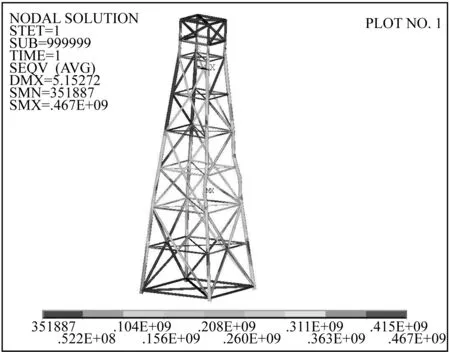
图4 极限状态时平台结构等效应力分布Fig. 4 Platform equivalent stress distribution in ultimate status

提取平台结构极限状态时的等效应力分布，如图4所示。由图4可知，由于垂直压力和水平载荷的联合作用，桩腿A2和B2在④至⑤层发生弯曲变形，从而导致平台结构发生较大的形变而无法继续承载。

4.3 平台倒塌全过程分析

为进一步分析平台结构进入极限状态后的力学特性，采用前述的方法，将确定的倒塌环境载荷(包括风载、波浪载荷、甲板上浪载荷)施加于LS-DYNA动力有限元模型中，对平台结构整个倒塌过程进行仿真，取计算时间为10 s，质量阻尼和刚度阻尼系数分别为0.133 1和0.018 8(通过模态分析获得平台前两阶固有频率分别为0.417和0.434 Hz)。由此，得到平台不同倒塌阶段的等效应力分布，如图5所示。

由图5(a)可知，极限状态后，平台桩腿A2和B2进一步压曲，导管架④至⑤层间K型斜撑发生大的弯曲变形，这些关键构件因过大的塑性变形而失去承载能力，从而导致平台结构内力发生重新分布，平台整体开始倾斜；随着进一步计算，平台构件截面塑性区不断扩展，t=5.25 s时，④至⑤层间的K型斜撑与桩腿A2和B2构件发生失效，且部分构件完全断裂，发生脱落，如图5(b)所示；此后，平台形成机构，失去稳定性，上部结构倾倒，并与⑤层和⑥层的杆件发生碰撞而使得平台进一步破坏，如图5(c)所示；最终在t=7.71 s时，伴随着构件的相继失效，平台完全倒塌于海底，倒塌形态如图5(d)所示。由以上分析可知，导管架④至⑤层的桩腿是平台结构的薄弱环节，在进行平台结构倒塌预防与控制时，可采用灌浆或卡箍对该弱点进行加固，或将该层的K型斜撑与对角斜撑改造为X型斜撑，以提高平台结构的鲁棒性。

提取平台K型斜撑(位置如图2(b)所示)的轴向应力如图6所示。由图6(a)和6(b)可知，由于倒塌过程构件受力状态复杂且相互作用，单元应力存在振荡现象，但观察图中曲线走势，可以发现倒塌过程中单元轴向应力方向改变，其承载机制由受压杆件演变为受拉杆件，这进一步说明倒塌中平台结构质量和刚度存在剧烈的重分布。此外，由图6(a)和6(b)可知，单元291和单元297轴向应力分别在t等于5.2和7.0 s时瞬间降为0 Pa，说明构件相继发生断裂失效，不再承受载荷。

纵观平台整个倒塌过程和受力分析可知，平台在自重和环境载荷的联合作用下，沿X轴发生倾斜，重心偏移，使得平台左侧桩腿承受过大的压弯载荷而发生屈服，随着塑性区的扩展，平台桩腿最终断裂，从而导致相邻构件因内力重新分布而发生过载，并相继破坏失效，最终使得平台形成机构而倒塌于海底。

5 结 语

1) 甲板上浪载荷对平台侧向载荷分布及结构响应影响较大，采用基于重现期为渐进加载方式的Pushover分析，能够有效考虑平台结构环境载荷分布的变化，获得平台结构真实的倒塌状态及对应的倒塌环境载荷。

2) LS-DYNA能够有效地实现导管架平台结构的倒塌全过程分析，再现平台从构件失效至局部结构破坏至最终整体倒塌的内力分布，对研究平台结构传力路径，确定构件失效顺序，进行平台倒塌控制与预防以及揭示平台结构的倒塌机理具有重要参考价值。

3) 将隐式算法与显式算法有效地结合，建立台风引起的极端环境载荷作用下导管架平台结构倒塌数值仿真技术流程，可为开展平台结构抗倒塌鲁棒性设计及理论研究提供技术支持。

[1] MMS. Assessment of fixed offshore platform performance in Andrew, Lili and Ivan[R]. 2006.

[2] MMS. Assessment of fixed offshore platform performance in Katrina and Rita[R]. 2007.

[3] 陈维杰, 陈国明, 朱本瑞, 等. 强台风下导管架平台风载荷数值仿真分析[J]. 中国海上油气, 2013, 25(3): 73-77. (CHEN Weijie, CHEN Guoming, ZHU Benrui, et al. Numerical simulation of wind load on jacket platform under strong typhoon [J]. China Offshore Oil and Gas, 2013, 25(3): 73-77. (in Chinese))

[4] 杨冬平, 陈国明. 海洋平台结构连续倒塌非线性动力响应分析[J]. 西安建筑大学学报：自然科学版, 2010, 42(2): 267-271. (YANG Dongping, CHEN guoming. Nonlinear dynamic response analysis of progressive collapse in offshore platform structure[J]. Xi’an Univ. of Arch. & Tech. (Natural Science Edition), 2010, 42(2): 267-271. (in Chinese))

[5] 朱本瑞, 陈国明, 刘康, 等. 深水导管架平台抗台风极限承载能力[J]. 石油学报, 2014, 35(1): 152-158. (ZHU Benrui, CHEN Guoming, LIU Kang, et al. Typhoon-resistant ultimate bearing capacity of deep-water jacket platforms[J]. Acta Petrolei Sinica, 2014, 35(1): 152-158. (in Chinese))

[6] PUSKAR F J, SPONG R E, KU A, et al. Assessment of fixed offshore platform performance in Hurricane Ivan[C]//Proceedings of the 2006 Offshore Technology Conference, Huston, 2006.

[7] GOLAFSHANI A A, EBRAHIMIAN H, BAGHERI V, et al. Assessment of offshore platforms under extreme waves by probabilistic incremental wave analysis[J]. Journal of Constructional Steel Research, 2011, 67(5): 759-769.

[8] 李辉, 赵伟. 结构连续倒塌分析研究现状及设计方法综述[J]. 山西建筑, 2011,37(21): 35-36. (LI Hui, ZHAO Wei. Overview on structure continuous collapse analysis research status and design methods[J]. Shanxi Architecture, 2011, 37(21): 35-36. (in Chinese))

[9] 胡晓斌, 钱稼茹. 多层平面钢框架连续倒塌仿真分析[J].力学与实践，2008, 30(4): 54-57. (HU Xiaobin, QIAN Jiaru. Progressive collapse simulation and analysis of a multi-story steel plane frame[J]. Mechanics in Engineering. 2008, 30(4): 54-57. (in Chinese))

[10] 陆新征, 江见鲸. 世界贸易中心飞机撞击后倒塌过程的仿真分析[J].土木工程学报， 2001, 34(6):8-10. (LU Xinzheng, JIANG Jianjing. Dynamic finite element simulation for the collapse of world trade center[J]. China Civil Engineering Journal, 2001, 34(6): 8-10. (in Chinese))

[11] API RP-2A WSD, Recommended practice for planning, design and constructing fixed offshore platforms — working stress design[S]. API recommended practice 2AWSD21th ed., 2007, Supplement 3.

[12] Golafshani A A, Bagheri V, Ebrahimian H, et al. Incremental wave analysis and its application to performance-based assessment of jacket platforms[J]. Journal of Constructional Steel Research, 2011, 67(10): 1649-1657.

[13] 陈团海, 陈国明, 许亮斌. 基于台风验证载荷的平台时变可靠性分析与更新[J]. 中国石油大学学报:自然科学版, 2011, 35(3): 129-134. (CHEN Tuanhai, CHEN Guoming, XU Liangbin. Time-dependent reliability analysis and updating of offshore platforms based on typhoon proof load[J]. Journal of China University of Petroleum: Edition of Natural Science, 2011, 35(3): 129-134. (in Chinese))

[14] VAN RAAIJ K, GUDMESTAD O T. Wave-in-deck loading on fixed steel jackets decks[J]. Marine Structures, 2007, 20(3): 164-184.

[15] VAN RAAIJ K. Dynamic behaviour of jackets exposed to wave-in-deck forces[D]. Norway: University of Stavanger, 2005.

[16] 董胜, 石湘. 海洋工程数值计算方法[M]. 青岛: 中国海洋大学出版社, 2007: 237-239. (DONG Sheng, SHI Xiang. Methods of numerical computation in ocean engineering[M]. Qingdao: China Ocean University Press, 2007: 237-239. (in Chinese))

[17] 白金泽. LS-DYNA3D 理论基础与实例分析[M]. 北京: 科学出版社, 2005. (BAI Jinze. LS-DYNA3D Theory and case analysis[M]. Beijing: Science Press, 2005. (in Chinese))

Simulation for entire collapse process of jacket platforms under extreme typhoon conditions

ZHU Benrui, CHEN Guoming, LIN Hong, LIU Hongbing, HUANG Chao

(Centre for Offshore Engineering and Safety Technology, China University of Petroleum, Qingdao 266580, China)

In view of the issue of the collapse problem caused by typhoon on fixed offshore structures, the simulation technology of the entire process for progressive collapse is introduced in this paper, which combines the advantages of implicit and explicit algorithms. A modified Pushover Analytical Method was proposed to determine the true collapse environmental load, which was based on the environment load return period, in order to take full account of changes in the distribution of lateral environmental load and the possible Wave-in-deck (WID) load. The equivalent models of implicit and explicit finite element were built by APDL to overcome the difficulties of calculation and exact exertion of wave load. On this basis, the entire collapse process of one jacket platform caused by strong typhoon was achieved using LD-DYNA, and the force redistribution and failure of components were clearly displayed, and the collapse mechanism was revealed. The studies provide a valuable reference for the anti-typhoon design and theory of jacket platforms.

typhoon; jacket platform; wave-in-deck; ultimate status; collapse mechanism; LS-DYNA; numerical simulation

P751

A

10.16483/j.issn.1005-9865.2015.02.012

1005-9865(2015)02-0097-08

2013-12-12

国家自然科学基金资助项目(51079159, 51209218)；中央高校基本科研业务费专项资金资助项目(13CX06079A, 12CX04069A).

朱本瑞(1986-)，男，山东曲阜人，博士研究生，主要从事海洋石油装备强度与可靠性研究工作。E-mail: zhubenrui@163.com.

陈国明。E-mail: offshore@126.com