声矢量阵阵元位置及幅相误差有源校正算法*

张　柯　王　闯　付　进

（1 许昌学院信息工程学院　许昌　461000）

（2 哈尔滨工程大学水声工程学院哈　尔滨 150001）

声矢量阵阵元位置及幅相误差有源校正算法*

张柯1†王闯1付进2

（1 许昌学院信息工程学院许昌461000）

（2 哈尔滨工程大学水声工程学院哈尔滨 150001）

针对声矢量阵幅相误差及阵元位置误差校正问题，基于特征分解法，提出一种简单实用的有源校正算法。该方法需要合作信源的至少3个方位信息，根据声矢量阵的通道特征，利用特征分解法构造矩阵方程组，通过矩阵运算得到声矢量阵阵元位置和幅相误差参数，从而实现对声矢量阵的校正。大量计算机仿真表明该校正算法具有良好的声矢量阵阵列误差参数估计性能。

声矢量阵，阵元位置误差，幅相误差，有源校正

1　引言

与声压阵相比，声矢量阵（Acoustic vector sensor array，AVSA）具有许多明显的优势，得到了众多国内外学者广泛的关注和浓厚的研究兴趣。在理想情况下，声矢量阵具有更高的方位估计性能和更加优越的目标检测能力，但是，当声矢量阵存在阵列误差时，基于声矢量阵的高分辨DOA估计算法，诸如声矢量阵MVDR［1］，MUSIC［2］和ESPRIT［3］等算法的测向性能将严重下降甚至失效。因此，在使用声矢量阵进行DOA估计之前，阵列误差的校正工作是不可或缺的。

针对声矢量阵阵列误差校正问题，国内外学者进行了卓有成效的研究［4-10］。针对声矢量阵存在阵元位置、幅相及阵元姿态误差的情况，文献［4］推导出了相应的理论表达式，并做了简要的仿真分析，但未提出任何校正方法。文献［5］分析了阵列误差对声矢量阵的影响，基于标量阵WF算法，提出了声矢量阵幅相误差的自校正算法，该算法具有和标量WF算法相同的性能。针对近场和远场情况下声矢量阵相位误差的校正问题，文献［6］和文献［7］分别基于子空间原理提出了相应的有源校正算法。文献［8］提出了一种声矢量阵阵元位置校正算法，该方法使用单个矢量水听器测得2个辅助声源的方位，然后基于子空间原理构造方程组并求出阵元位置参数，该算法的阵元位置误差参数估计性能取决于单矢量水听器的测向精度。针对声矢量阵阵元姿态误差，文献［9］提出了一种有源校正算法，该算法利用方位精确已知的校正源对声矢量阵阵元姿态误差进行校正。在文献［9］的基础上，文献［10］提出了声矢量阵阵元姿态自校正算法，该算法可实现阵元姿态误差参数和信源DOA的联合估计，且具有良好的参数估计性能。

在实际工程中，安装误差、平台振动将导致声矢量阵产生阵元位置误差；接收通道滤波放大系统幅频、相频不一致导致声矢量阵产生幅度和相位误差。声矢量阵阵元位置误差和幅相误差往往是同时存在的，现有的算法仅仅是针对某一种误差提出了解决方法，与实际工程的需求不符。针对声矢量阵阵元位置误差和幅相误差同时存在的情况，本文提出了一种有源校正算法，该算法可实现声矢量阵阵元位置和幅相误差的联合校正，具有良好的阵列误差参数估计性能。

2　声矢量阵阵列输出模型

假设M个声矢量传感器以间距d排列成线形阵列，放置于各向同性的噪声环境中，在以阵列轴线的法线为参考的θk（k=1，2，…，K）方向有K个波长为λ的远场窄带平面波入射。当该声矢量阵同时存在阵列位置和幅相误差时，声矢量阵的输出模型为

3　联合校正算法

综合考虑阵元位置及幅相误差，阵列流形可看出是以阵元位置参数及幅相参数为参量而以入射角参数为变量的函数。参数化方法让原本复杂的问题简单化，大大地减小了校正的工作量。我们采用一个辅助源Ss（t）对阵元位置及幅相误差进行联合校正，在校正过程中，该辅助源要放置在K个不同的方位，即｛θ1，θ2，…，θK｝，信号功率为，噪声功率为，并已知校正源的信号波形，则第k（k=1，2，…，K）个位置的校正源的声矢量阵输出为

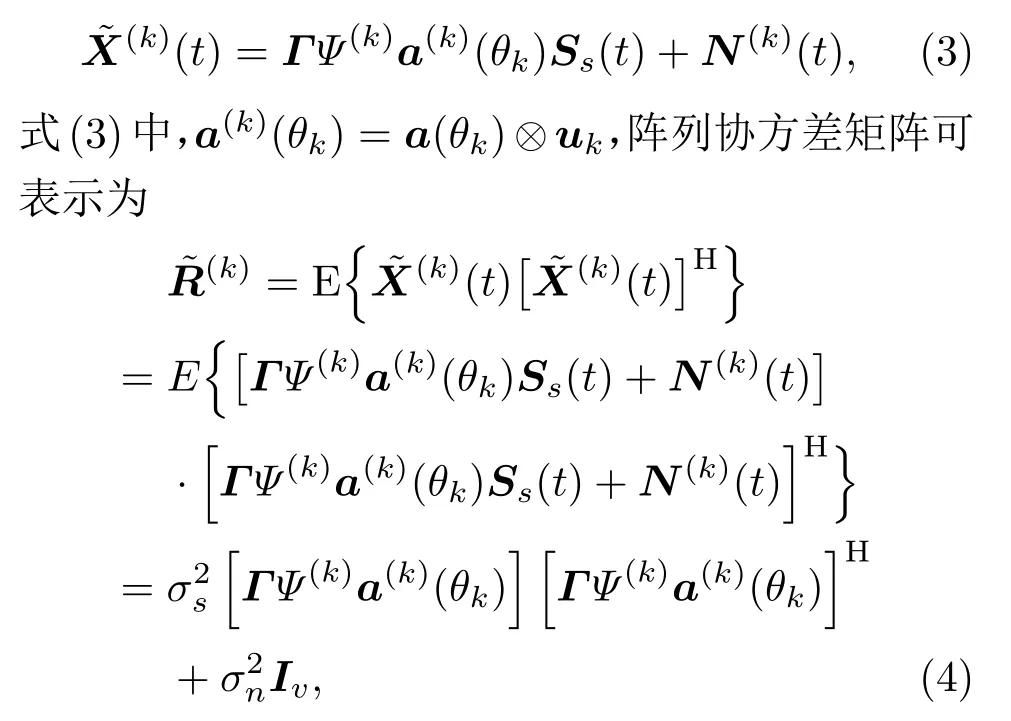
式（4）中，Iv为声矢量阵噪声相关矩阵，其具体形式为

为方便推导，式（18）～（20）可改写为

显然，利用式（24）～（26）中任意一个联立方程组均可解出阵元位置误差［ΔX，ΔY］。为了充分利用已知信息和得到更加精确的参数估计，将式（24）～（26）改写为

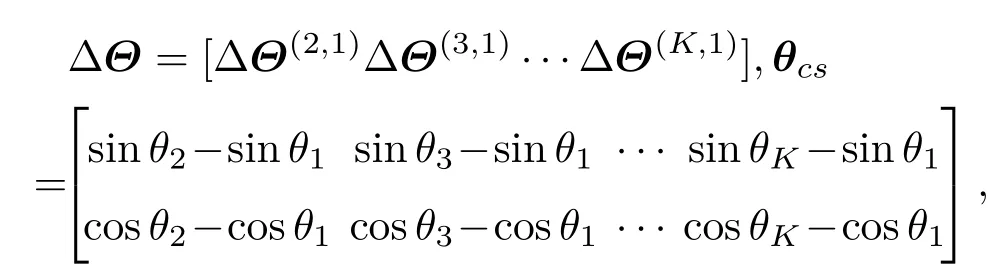
ΔΘ是测量值，θcs为已知值，故只需Rank（θcs）=2，就可解得ΔX和ΔY。显然，当K=3时，式（28）有唯一解，当K＞3时，式（28）为超定方程，根据最小二乘原则，可得阵元位置参数的估计值为

式（33）～（35）中，m=1，2，…，M，通过式（29）～（35）可估计出阵元位置及幅相误差参数。需要注意的是，在实际的操作中，θk（k=1，2，…，K）之间的差值要尽量大些，这是因为θk之间的差值越小，则矩阵θcs的列向量相关程度越高，求广义逆时，解的性能就越差，此时所得到的阵元位置参数误差就越大，因此阵列相位参数的估计精度也将受到影响。

4　计算机仿真

在下列仿真实验中，假设一个6元声矢量阵沿x轴以d=λ/2等间距布放，设定某一校正声源分别在方位10°，60°和-60°处发射信号，设第一个阵元为参考阵元，其阵元位置、声压通道的增益及相位分别为（x，y）=（0，0），gp1=1和φp1=0，阵元位置x和y轴方向的误差服从［-0.2λ，0.2λ］内的随机分布，阵列增益误差为10%（相对于单位增益），即除参考阵元外的声矢量阵阵列通道的增益服从［0.9，1.1］内的随机分布，除参考阵元外的声矢量阵阵列的相位服从［-0.5，0.5］rad内的随机分布。

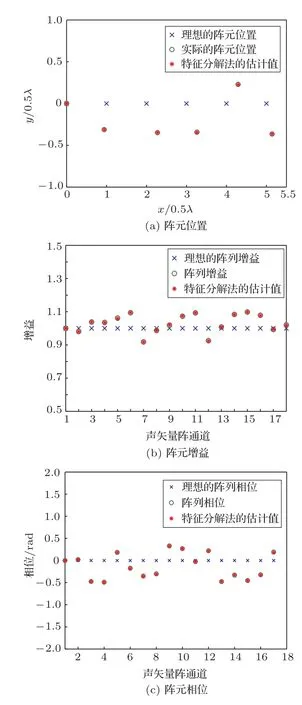
图1　声矢量阵误差参数理想值、实际值及估计值Fig.1 The nominal，actual and estimated array factors of AVSA

图1表示声矢量阵阵元位置及幅相参数的理想值、实际值和本文算法的估计值的分布情况，其中，信噪比为30 dB，快拍数为100。从图1（a）中可以看出，本文算法得到的声矢量阵阵元位置的估计值与实际值重合于一点，通过第3个阵元位置的放大图可以看出，本文算法得到的阵元位置估计值与实际值的偏差很小。与图1（a）中情况类似，在图1（b）和图1（c）中，本文算法得到的阵列增益及相位估计值与阵列增益及相位实际值的偏差同样很小。

假设两个相互独立的远场声源分别从方位-20°，30°入射到该声矢量线阵，信噪比为30 dB，快拍数为100。基于该声矢量阵校正前后的MUSIC空间谱估计结果如图2所示。从图2可以看出，未校正时的MUSIC空间谱谱峰高度仅有5 dB，方位角的估计有5°左右的偏差，这表明未校正时的声矢量阵测向性能很差。而经过本文算法校正后的MUSIC空间谱的谱峰高度将近50 dB，且方位角估与真实方位一致。

图3表示声矢量阵阵元位置及幅相参数估计的均方根误差在不同信噪比及快拍数的条件下的变化曲线，除信噪比和快拍数外，其它仿真条件如图1所示。其中，Ω取200，声矢量阵阵元位置、增益及相位估计的均方根误差可分别表示为

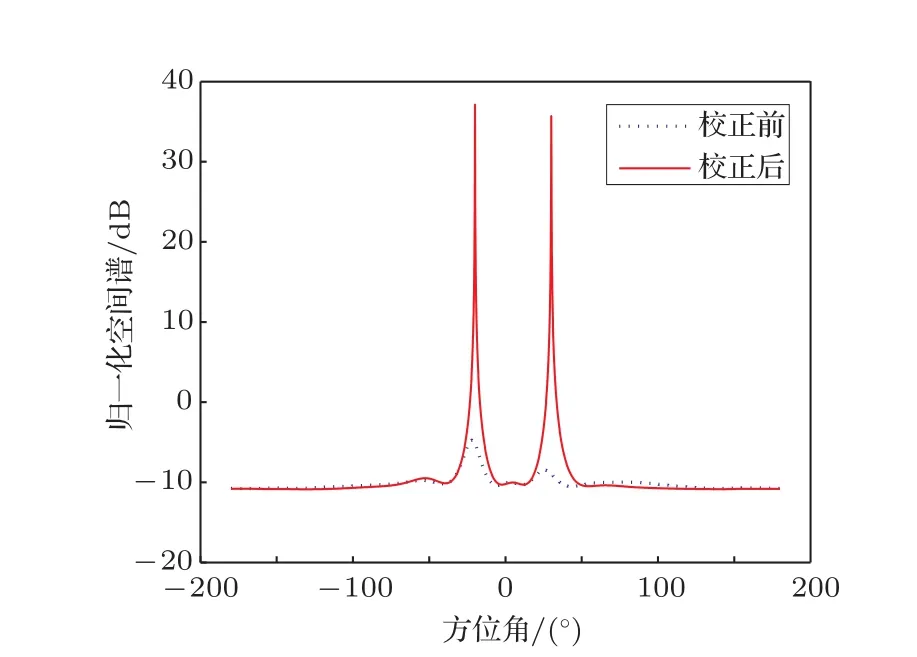
图2　声矢量阵校正前后的空间谱估计Fig.2 Spatial spectrum of calibration and uncalibratied AVSA

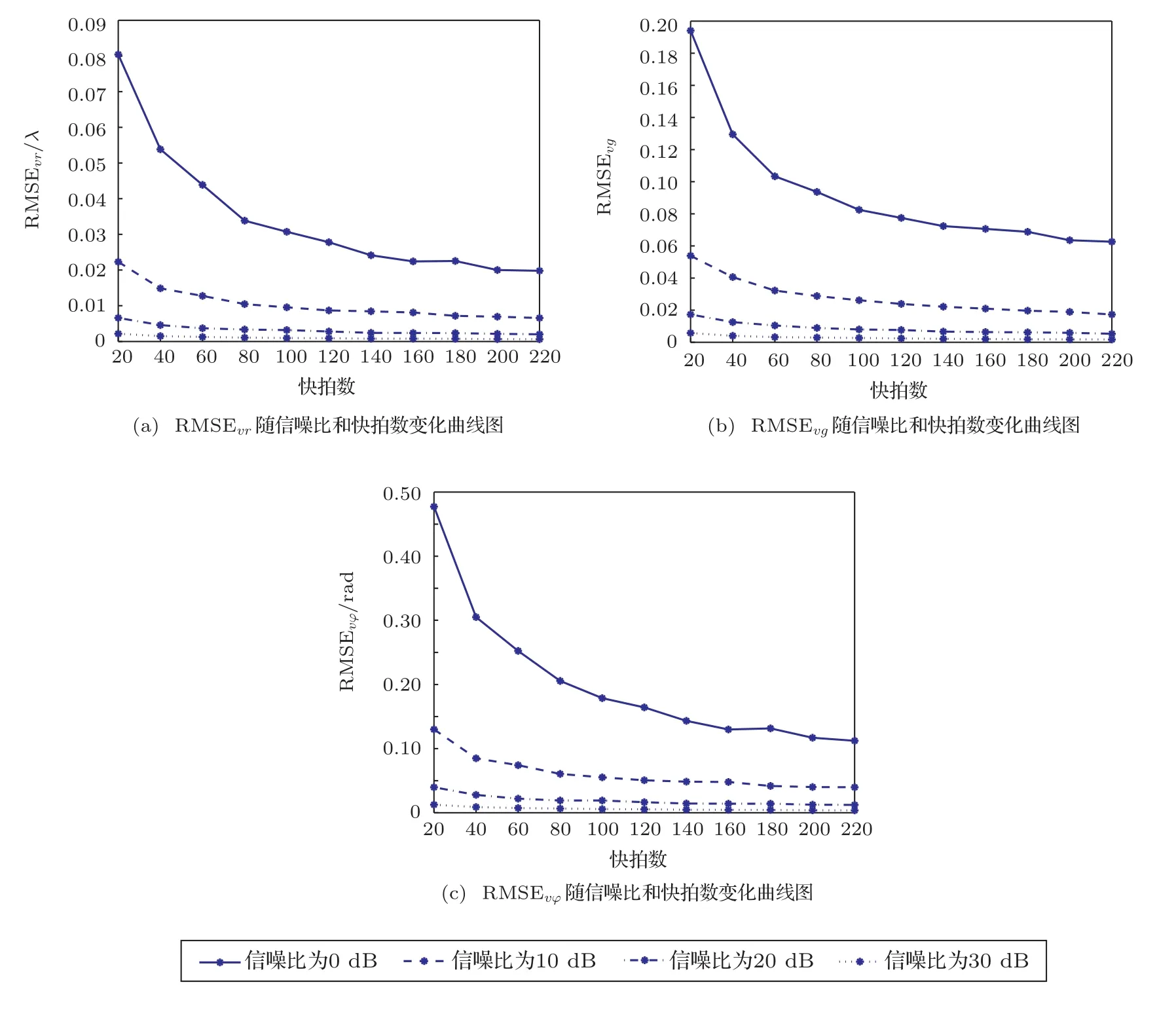
图3　声矢量阵参数均方根误差随信噪比和快拍数变化曲线Fig.3 RMSE of AVSA factors versus SNR and snapshots

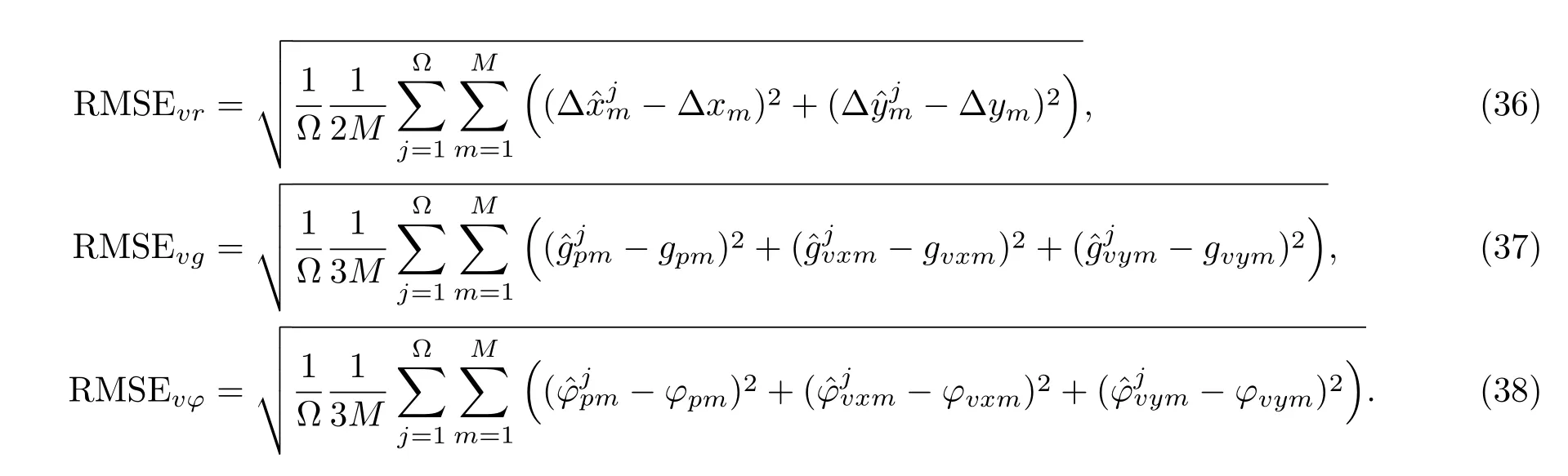
从图3（a）中可以看出，当信噪比分别为0 dB，10 dB，20 dB及30 dB时，由本文速度法得到的RMSEvr曲线随快拍数的增加，相应的RMSEvr值随之减小，在高信噪比条件下，本文算法具有良好的阵元位置参数估计性能。在图3（b）和3（c）中，与RMSEvr曲线变化情况相似，由本文算法得到RMSEvg值和RMSEvφ值随信噪比和快拍数的增加而减小。在实际工程应用中，可选取较高的信噪比和快拍数，以获得高精度的阵列误差参数估计，使声矢量阵达到良好的校正效果。

5　水池实验

2013年12月，在哈尔滨工程大学消声水池做了声矢量4元均匀直线阵的实验，阵元间距为0.5 m，声源与阵中心相距11 m，声矢量阵与声源均在水下2 m，位于同一平面上，校正源是频率为3 kHz的单频信号，采样频率为20 kHz，信噪比约为40 dB，快拍数为100，图4为实验示意图。校正源方位θ分别为85°，100°和115°①经大量数据分析发现，由于声矢量水听器尺寸较大，声源入射方向与声矢量阵法线方向夹角越大，阵元之间的散射就越严重，这对阵列校正工作有较大的影响。故选择的校正源方位和待测声源方位与阵列法线方向偏差不大，其目的是尽量减小散射对阵列校正带来的影响。，待测声源方位为90°校正前后的测向结果如图5所示。

从图5可以看出，未校正时，声矢量阵MUSIC谱的谱峰高度仅为3.5 dB，方位的估计值为97°，与真实值偏差7°；经过本文算法校正后声矢量阵MUSIC谱线也基本重合，校正后，方位的估计值为91°，与真实值偏差仅1°，谱峰高度也有相应提高，由于阵元间散射及声障板的影响，声矢量阵校正效果不佳，若采用尺寸较小的MEMS声矢量传感器或光纤声矢量传感器，可忽略阵元间的散射影响，取得良好的校正效果。

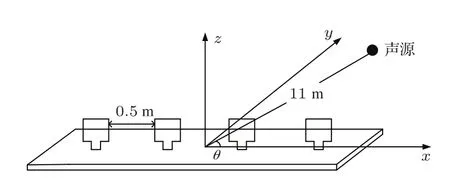
图4　声矢量阵消声水池试验示意图Fig.4 AVSA Experiment in anechoice water tank

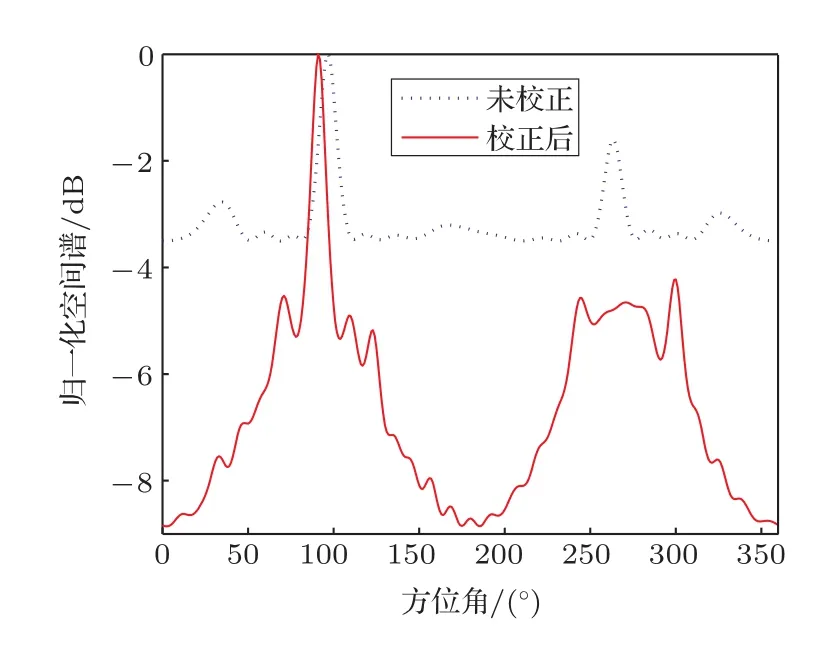
图5　声矢量阵校正消声水池试验结果Fig.5 Result of AVSA calibration experiment made in anechoice water tank

6　结论

本文针对声矢量阵同时存在阵元位置和幅相误差的情况，提出了一种高精度的阵列误差参数估计方法，在高信噪比条件下，该方法具有良好的阵列误差参数估计性能。针对幅相误差随校正源频率变化的情况，可使用宽带校正源对声矢量阵进行校正，把宽带信号分成若干窄带，对每个窄带对应的幅相误差使用本文算法进行校正。在实际工程应用中，该方法简单实用，具有良好的应用前景。

［1］时洁，杨德森.矢量阵相干宽带MVDR聚焦波束形成［J］.系统仿真学报，2011，39（3）：473-477.

SHI Jie，YANG Desen.Coherent broadband MVDR focusedbeamformingbasedonvectorsensorarray processing［J］.Journal of System Simulation，2011，39（3）：473-477.

［2］何希盈，程锦房，姚直象，等.矢量水听器阵列矩阵空域预滤波MUSIC算法［J］.华中科技大学学报（自然科学版），2011，39（3）：71-74.

HE Xiying，CHENG Jinfang，YAO Zhixiang，et al. MUSIC algorithm of spatial prefiltering for vector hydrophones in an array matrix［J］.J.Huazhong Univ.of Sci. &Tech.（Natural Science Edition），2011，39（3）：71-74.

［3］王绪虎，陈建峰，韩晶，等.基于ESPRIT算法的矢量水听器阵方位估计性能分析［J］.系统工程与电子技术，2013，35（3）：481-486.

WANG Xuhu，CHEN Jianfeng，HAN Jing，et al.Performance analysis of DOA estimation of vector hydrophone array based on ESPRIT algorithm［J］.Systems Engineering and Electronics，2013，35（3）：481-486.

［4］刘凯，梁国龙，张光普，等.初探阵列误差对矢量阵波束形成系统的影响［J］.系统仿真学报，2012，24（4）：848-853.

LIU Kai，LIANG Guolong，ZHANG Guangpu，et al.Exploratory analysis to influence of array errors on vectorsensor array beam-forming system［J］.Journal of System Simulation，2012，24（4）：848-853.

［5］王鹏.基于MEMS矢量水听器阵列的声目标定向定位技术研究［D］.太原：中北大学，2013.

［6］杨德森，时洁.单辅助源矢量阵相位误差校正方法［J］.声学技术，2009，28（2）：101-102.

YANG Desen，SHI Jie.Method for phase errors calibration in vector array processing［J］.Technical Acoustics，2009，28（2）：101-102.

［7］刘云，金贝利.矢量阵一种简单的相位误差校正方法［J］.计算机仿真，2010，27（8）：351-354.

LIU Yun，JIN Beili.A simple method for phase error correction in the vector hydrophone array［J］.Computer Simulation，2010，27（8）：351-354.

［8］梁国龙，张锴，吴文峰.基于子空间拟合的声矢量阵阵型校正算法及DOA估计［J］.兵工学报，2012，33（9）：1112-1117.

LIANG Guolong，ZHANG Kai，WU Wenfeng.Correction algorithm of acoustic vector sensor array and DOA estimation based on subspace fitting［J］.Acta Armamentarii，2012，33（9）：1112-1117.

［9］LIM H S，RAMESHCHANDRA K，TOH W S.Estimation and compensation of rotation perturbation in linear 2D acoustic vector sensor array［C］.Oceans Conf.IEEE Spain，2011.

［10］梁国龙，张柯，安少军，等.声矢量阵阵元姿态误差自校正算法研究［J］.兵工学报，2014，35（8）：1236-1242.

LIANG Guolong，ZHANG Ke，AN Shaojun，et al.Research on self-calibration algorithm for attitude errors of acoustic vector sensor array［J］.Acta Armamentarii，2014，35（8）：1236-1242.

Active calibration algorithm for location，gain and phase of acoustic vector sensor array

ZHANG Ke1WANG Chuang1FU Jin2

（1 School of Information Engineering，Xuchang University，Xuchang 461000，China）

（2 College of Underwater Acoustic Engineering，Harbin Engineering University，Harbin 150001，China）

Consider calibration for location，gain and phase errors of acoustic vector sensor array（AVSA），a simple and practical active calibration algorithm based on eigen decomposition was proposed.The proposed algorithm requires at least three DOAs（Direction of arrival）information from the cooperation source.The channel feature of AVSA and eigen decomposition are exploited to construct matrix equations，the location，gain and phase factors of AVSA are obtained by matrix operations and AVSA can be calibrated by the factors. Extensive computer simulations show that the proposed algorithm has good estimation performance for array errors of AVSA.

Acoustic vector sensor array，Location errors，Gain and phase errors，Active calibration

TN911.7

A

1000-310X（2015）05-0457-08

10.11684/j.issn.1000-310X.2015.05.012

2014-12-18收稿；2015-05-05定稿

*国家自然科学基金（51209059，51279043），黑龙江省普通高等学校青年学术骨干支持计划（1253G019）作者简介：张柯（1984-），男，河南许昌人，博士，讲师，研究方向：阵列信号处理。

E-mail：zhangke1127@126.com